基于动态直觉模糊VIKOR群决策的冷链供应商选择研究
2015-11-22胡建平
李 梅,吴 冲,胡建平
(1.哈尔滨工业大学管理学院,黑龙江 哈尔滨150001;2.广西师范学院物流管理与工程学院,广西 南宁530001;3.广东工贸职业技术学院,广东 广州510510)
随着物流行业的深入发展和人们生活水平的不断提升,高附加值的冷链物流在流通领域扮演着越来越重要的作用。所谓冷链物流[1],是指冷藏冷冻类物品在生产、储存、运输、再加工以及销售的全过程中始终处于规定的低温环境下,以保证物品质量和性能的供应链系统。供应商选择是冷链物流中下游企业(客户)采购流程的重要环节。能否全面客观地对其进行选择评价,并与之建立稳定的联盟伙伴关系,关系到下游企业(客户)的采购效用,也关系到冷链物流的运营效率。
目前,国内外学者对供应商选择进行了大量的研究,主要集中在两个方面:一是供应商选择的指标选取;二是供应商评价的模型方法[2]。在供应商选择的指标体系中,比较集中的指标主要有供应商的质量、价格、服务能力、财务水平、关系管理、选址及文化适应[3-5]等;供应商选择的评价方法则集中于数据包络分析法(DEA)、网络层次分析法(ANP)、模糊评价法、理想点决策法(TOPSIS),以及这些方法的有效结合[6-9]等。然而,针对冷链物流供应商选择的文献鲜见。本文借鉴并改进已有的研究成果,构建冷链物流供应商选择的评价指标体系,并采用动态直觉模糊VIKOR 群决策模型对其进行研究分析,为冷链物流供应商选择提供一种新的算法。一方面,决策评价过程引入动态直觉模糊数,将传统的静态评价升级为动态评价,同时考虑了决策过程中的不确定性和决策专家打分的犹豫度水平,使属性评价值合理性增强,更加符合实际工作需求;另一方面,使用VIKOR 决策方法进行综合评价,该方法是一种基于理想点的决策方法,它的基本思想是以群体效用最大化及个体遗憾最小化为出发点,根据各评估方案与理想方案的接近程度来排列方案的优先顺序并进行方案优选,同时兼顾了决策者的偏好影响,从而得到更合理的决策效果。
1 基于动态直觉模糊VIKOR 群决策模型基础理论
1.1 直觉模糊集及运算
定义1[10]设X 是一个非空集合,则论域X 上的直觉模糊集A 可表示为

其中,μA(x)和vA(x)分别为X 元素中x 属于A 的隶属度和非隶属度,即μA:X→[0,1],x∈X→μA(x)∈[0,1],vA:X→[0,1],x∈X→vA(x)∈[0,1]。同时,满足0≤μA(x)+vA(x)≤1;则πA=1-μA(x)-vA(x)为X 元素中x 属于A 的犹豫度或不确定度。显然,对于任意的x∈X,都有0≤πA(x)≤1。
设α = (μa,va)为直觉模糊数,且设Θ 为全体直觉模糊数的集合[11]。显然,α+= (1,0)为最大的直觉模糊数,α-= (0,1)为最小的直觉模糊数。
直觉模糊集的一些基本运算法则如定义2 所示:
定义2[12]若α1= (μa1,va1)和α2= (μa2,va2)均为直觉模糊数,则
1) α-= (va,μa);
2) α1∧α2={min(μa1,μa2),max (va1,va2)};
3) α1∨α2={max(μa1,μa2),min (va1,va2)};
4) α1⊕α2=(μa1+μa2-μa1μa2,va1va2);
5) α1⊗α2=(μa1μa2,va1+va2-va1va2);
6) λα=(1-(1-μa)λ,vαλ,λ>0);
7) αλ=(μaλ,1-(1-va)λ,λ>0)。
1.2 直觉模糊集成算子[11]
定义3[13]设αj=(μaj,vaj)(j=1,2,…,n)是直觉模糊数,且设IFWA:Θn→Θ,
若
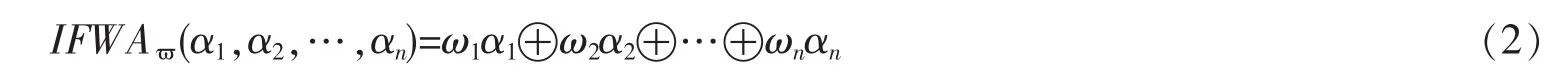
定理1[13]设aj=(μaj,vaj)(j=1,2,…,n) ,则有

且由IFWA 算子集成所得到的值也是直觉模糊数。
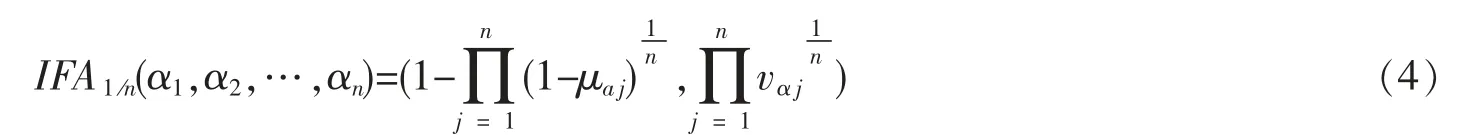
1.3 直觉模糊数的距离测度公式
若a1= (μa1,va1)和a2=(μa2,va2)为两个直觉模糊数,则

为a1和a2的距离。
1.4 动态直觉模糊多属性群决策问题描述
动态直觉模糊多属性群决策问题可以描述为:在tk(k=1,2,…,r)个时段中,由p 人组成的决策专家团Dl(l=1,2,…,p)从一系列备选方案Ai(i=1,2,…,m)中,依据评价准则Cj(j=1,2,…,n),给出含有直觉模糊数形式的评价信息,并对方案进行决策优选。设ωk表示各个时段tk的权重,λkl表示tk时段决策者Dl的权重,ζkl表示tk时段指标Cj的权重。则tk时段决策者Dl的决策矩阵可以表示为

表1 tk 时段决策者Dl 的直觉模糊决策矩阵Tab.1 Intuitionistic fuzzy decision-making matrix of Dl in period tk
其中,(μklmn,vklmn) 表示tk时段决策者Dl给出的Ai方案在Cj指标下的直觉模糊评价值,μklmn和vklmn分别表示评价值的隶属度和非隶属度,且
1.5 动态直觉模糊数的加权平均DIFWA 算子[14]
将公式(2)和(3)加以推广,形成动态直觉模糊数的加权平均算子DIFWA,设α1,α2,…,αr为r 个不同时段tk(k=1,2,…,r)状态下的直觉模糊数,且ωk为各个时段tk的权重,则称
进一步简化T-Map空间域,以获得不同交点轴线偏差的2维坐标波动范围,对T-Map的3维空间域再次进行降维。依次设定λF中和任意两项为0进行降维,可得到6个2维空间域,利用式(12)可得2维空间域边界分别为:
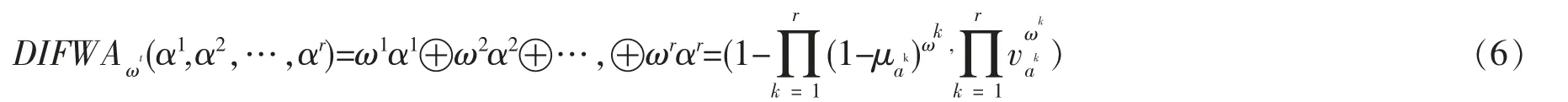
为动态直觉模糊数的加权平均DIFWA 算子。
2 动态直觉模糊VIKOR 群决策模型的构建
首先,组织决策专家小组分阶段采集冷链物流供应商的信息并根据指标内容对其进行打分,接着根据IFWA 算子将各个时段专家打分的直觉模糊信息与其权重信息集结,得到每个时段的群评价信息矩阵,再根据DIFWA 算子将各个时段的群评价信息与指标权重信息集结,得到综合评价的直觉模糊矩阵。在此基础上,将VIKOR 决策方法[15]引入到模型中,构建动态直觉模糊VIKOR 群决策模型。具体步骤:
步骤1 根据决策专家的打分矩阵,利用IFWA 算子(3),计算每个时段的群评价信息矩阵;
步骤2 根据DIFWA 算子(6),将各个时段的群评价信息与指标权重信息集结,得到综合评价的直觉模糊矩阵;
步骤3 分别定义直觉模糊正理想解x+和负理想解x-,即

其中,α+= (1,0),α-= (0,1)。
步骤4 根据直觉模糊距离测度公式(5),计算各供应商的群体效益值Si和个体遗憾度Ri,公式:
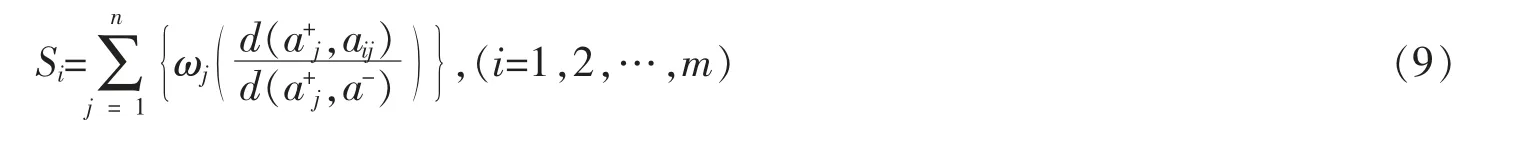

步骤5 计算各待评价供应商的折衷排序值
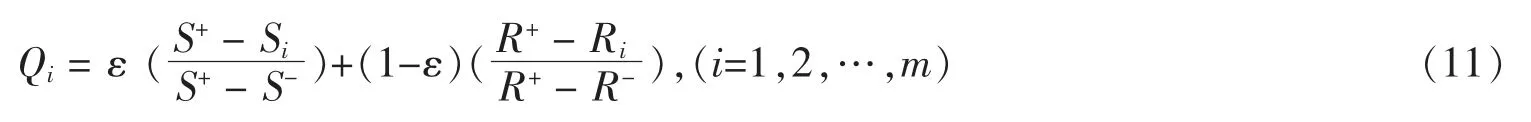
式中,ε 为折衷排序系数,ε∈[0,1],若ε>0.5,则表示方案群体效益的比重高于个体遗憾度的比重;反之亦然。通常情况下,取ε = 0.5。
步骤6 按照VIKOR 决策法的决策准则对备选供应商进行排序,Qi值越大,说明方案越差;Qi值越小,说明方案更优。同时,若存在Q′-Qmin≥1/(m-1),则说明最小解所对应的方案为最优,其中Q′为次小解,Qmin为最小解,m 为对比方案个数。
3 冷链物流供应商选择指标体系的建立
供应商选择是企业与其供应商建立和保持长期合作关系的基础。一般来说,传统供应商的选择是通过供应商供货的产品价格、产品质量、供货及时性、交货期的稳定性及客户服务等各项评定指标进行综合分析的。冷链物流供应商选择更是在这基础上把供应商的冷链能力和水平作为首要因素而提出的。通过选择合适的冷链供应商,并与之建立紧密长久的合作关系,不仅可以降低下游企业(客户)成本、减少库存、提高现金流量、提升物流专业化水平,更能满足冷链商品消费者对于产品高品质享受的预期。
通过归纳梳理大量文献,并结合冷链物流的发展现状,综合专家意见,最终确立了冷链物流供应商选择的18 项指标,并将其整合为5 项指标(C1~C5)。由于指标数量较多,为了便于专家快速、准确、全面打分,设计了冷链物流供应商选择评价指标的体系图,如图1所示。
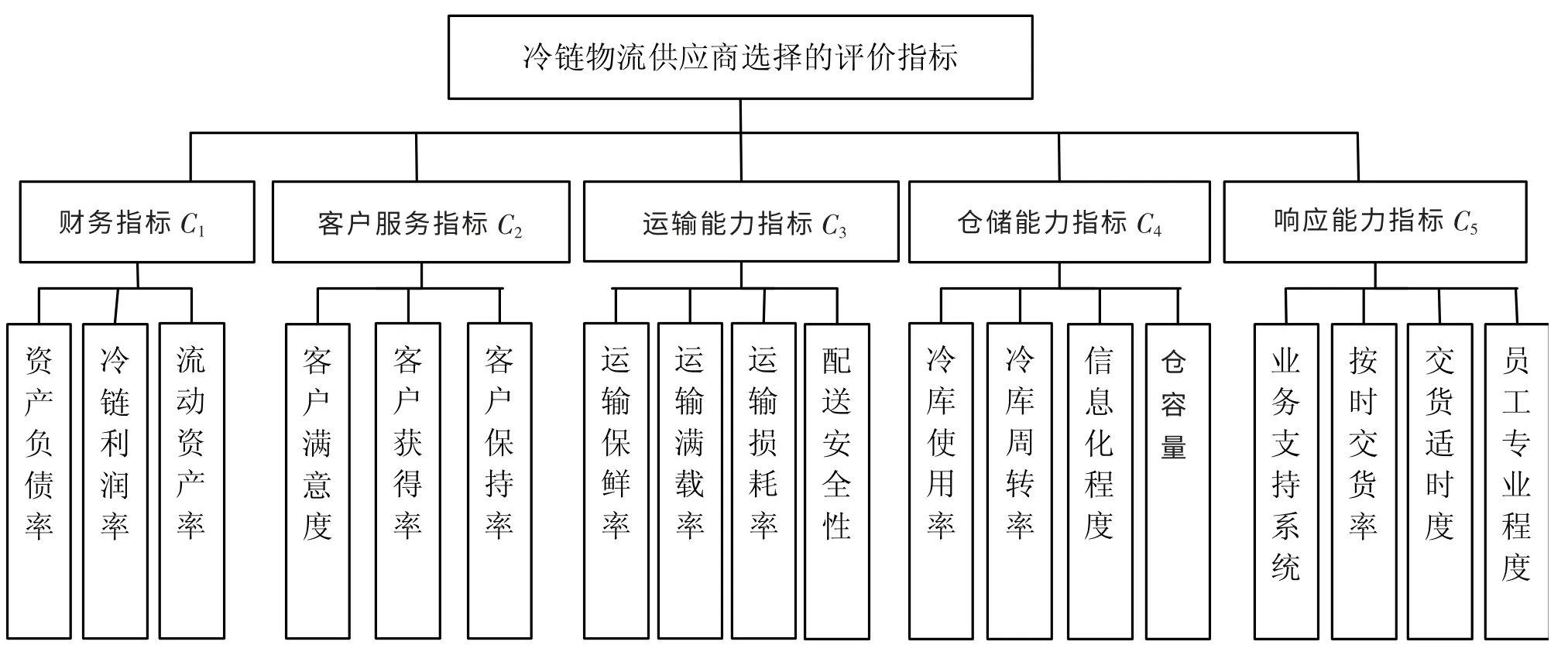
图1 冷链物流供应商选择的评价指标体系Fig.1 Evaluation index system of cold logistics supplier selection
4 算例分析
某冷链物流企业对5 个潜在的供应商(A1,A2,…A5)分资格审查t1,初步沟通t2,和深入调研t3,3 个阶段进行优选,3 个决策专家小组(D1,D2,D3)分别从财务指标(C1)、客户服务指标(C2)、运输能力指标(C3)、仓储能力指标(C4)及响应能力指标(C5)等5 个维度对其进行评价。评价值均为直觉模糊数,且设ωk表示各个时表示tk时段决策者Dl的权重,λ1= [0.40,0.28,0.32],λ2=段tk的权重,ω3[0.30,0.35,0.35],λ3= [0.40,0.30,0.30]; ζkl表示tk时段指标Cj的权重,ζ = [0.30,0.17,0.13,0.26,0.14]。专家决策小组在各阶段对5 个供应商的评价值如表2~表4所示。
下面利用本文所建模型进行求解。
首先,根据决策专家的打分矩阵,利用IFWA 算子(3),计算每个时段的群评价信息矩阵,如表5所示。

表2 专家决策小组在t1 阶段对5 个供应商的评价值Tab.2 Evaluation values for the five suppliers made by expert decision group in t1 stage

表3 专家决策小组在t2 阶段对5 个供应商的评价值Tab.3 Evaluation values for the five suppliers made by expert decision group in t2 stage

表4 专家决策小组在t3 阶段对5 个供应商的评价值Tab.4 Evaluation values for the five suppliers made by expert decision group in t3 stage
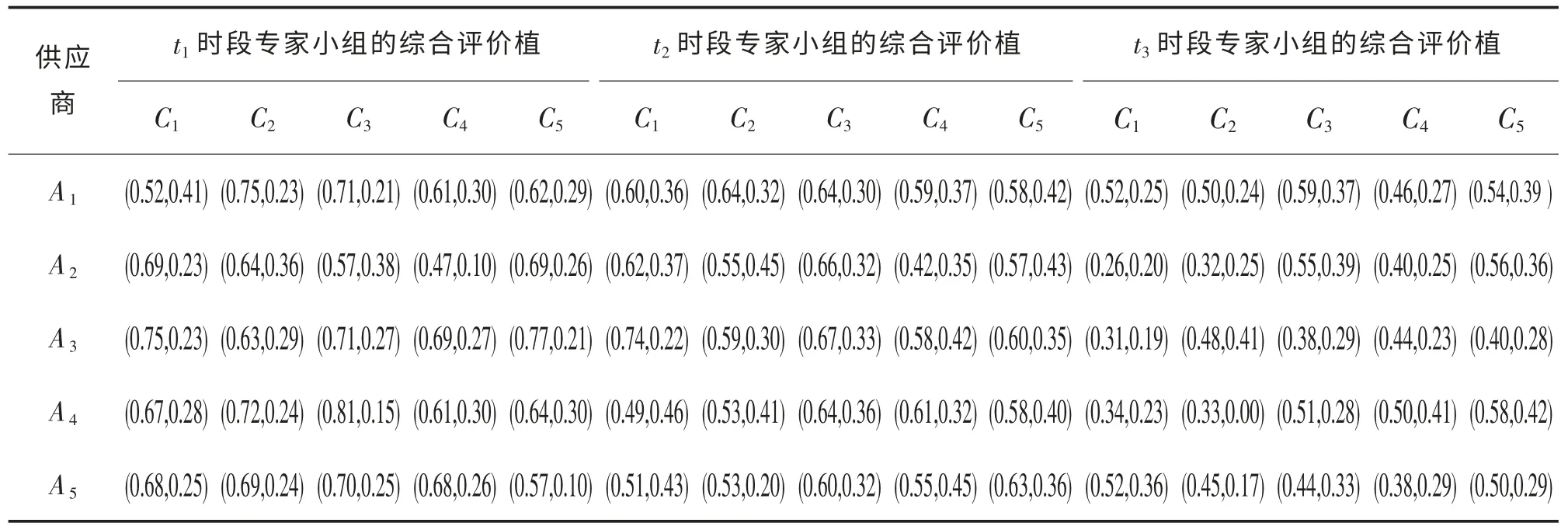
表5 群评价信息矩阵Tab.5 Group evaluation matrix
然后,根据DIFWA 算子(6),将各个时段的群评价信息与指标权重信息集结,得到综合评价的直觉模糊矩阵,如表6所示。

表6 直觉模糊矩阵的综合评价Tab.6 Comprehensive evaluation of intuitionistic fuzzy decision-making matrix
接着,根据步骤3,4,5 分别定义直觉模糊正理想解x+和负理想解x-,通过直觉模糊距离测度公式(5),计算各供应商的群体效益值Si和个体遗憾度Ri,并依据VIKOR 决策法的决策准则对备选供应商进行排序,Qi值越大,说明方案越差;Qi值越小,说明方案更优。结果如表7所示。

表7 待选择供应商的Si、Ri 及Qi 值Tab.7 Si,Ri and Qi of five suppliers
最后,进行最优解的判断,Q′-Qmin= 0.4139-0.0000=0.4139≥1/(m-1)=0.250,故满足最优解判断标准,A1为最优冷链物流供应商。
使用TOPSIS 方法[16]进行供应商优选,结果与本文一致,即A1>A3>A5>A4>A2,从而说明了本文所构建方法的可行性和有效性。此外,在决策专家打分的过程中,若存在多种类型的数据,如实数、区间数及直觉模糊数并存的情况,与TOPSIS 方法相比,选择VIKOR 决策方法可以有效降低数据间的不可公度性,提高决策的合理性。
5 结束语
本文基于冷链物流供应商选择的评价指标体系,构建了动态直觉模糊VIKOR 群决策模型,提出了在时间权重、专家权重及指标权重已知的条件下进行动态直觉模糊多属性群决策的方法和步骤,并通过一个算例证明该方法是有效可行的,为物流供应商选择提供了一种新的思路。本决策方法也可推广到人员动态评价、服务质量动态评价及医疗诊断等领域,具有比较广阔的应用前景和实用价值。
[1]毋庆刚.我国冷链物流发展现状与对策研究[J].中国流通经济,2011(2):24-28.
[2]袁宇,关涛,闫相斌,等.基于混合VIKOR 方法的供应商选择决策模型[J].控制与决策,2014,29(3):551-560.
[3]SANJAY JHARKHARIA,RAVI SHANKAR.Selection of logistics service provider: An analytic network process (ANP) approach
[J].The International Journal of Management Science.2007,35(3):274-289.
[4]綦振法,程钧谟,徐福缘.供应商综合实力的指标评价体系及模糊判断[J].数学的实践与认识,2006,36(8):13-18.
[5]李柏生.供应商评价指标体系在ERP 系统中的建立[J].电子技术与软件工程,2014(1):107.
[6]胡军,余文芳,陈云南.基于TOPSIS 理论的企业供应商选择应用[J].统计与信息论坛,2008(11):65-70.
[7]黄细燕,徐玉萍.基于分类预处理的协同供应商模糊综合评价[J].华东交通大学学报,2014,31(6):126-130+142.
[8]孙璐.基于SODM-TOPSIS 的物流供应商选择研究[J].物流技术,2013,32(12):333-335.
[9]黄晋川,范建平.基于AHP 和DEA 的绿色建材供应商选择研究[J].项目管理技术,2014(10):88-92.
[10]ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[11]徐泽水.直觉模糊信息集成理论及应用[M].北京:科学出版社,2008.
[12]ATANASSOV K.New operations defined over the intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1994,61(2):137-142.
[13]XU Z S.Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making[J].Fuzzy Optimization and Decision Making,2007,6(2):109-121.
[14]XU Z S,YAGER R.Dynamic intuitionistic fuzzy multi-attribute decision making [J].International Journal of Approximate Reasoning.2008,48(1):246-262.
[15]SANAYEI A,MOUSAVI S F, YAZDANKHAH A.Group decision making process for supplier selection with VIKOR under fuzzy environment[J].Expert Systems with Applications,2010,37(1):24-30.
[16]南江霞,李登峰,张茂军.直觉模糊多属性决策的TOPSIS 法[J].运筹与管理,2008,17(3):34-37.
