地震作用下列车-桥梁空间耦合系统动力响应分析

沙 峰，姚林泉，程 曦

（苏州大学城市轨道交通学院，江苏 苏州215131）

地震是一种突发的地壳剧烈运动，世界范围内几乎每年都要发生多次不同震级的地震，尤其最近几年地壳运动非常活跃，而我国作为地震灾情严重的国家，自20世纪以来，平均大约每3年就要发生2次七级以上地震［1］。地震，尤其是震级与能量较大的地震，给人的生命财产带来严重的危害。对于铁路系统而言，较大的地震发生时，巨大的地震能量会导致路面开裂、地基变形、轨道弯曲、桥梁坍塌，列车脱轨，引发安全事故。随着我国高速铁路的飞速发展，铁路桥梁在线路中的比重逐年增加，地震发生时列车过桥的概率随之变大。随着地震烈度的增强和列车运行速度的增加，车桥耦合系统的动力响应变得愈发复杂［2］，因此，分析地震作用下车桥系统动力响应具有重要意义。

自上世纪以来，国内外许多学者对地震作用下轨道车辆在桥梁上的行车性能和桥梁的动力响应开展了大量的理论和试验研究工作［3-5］，研究主要集中在地震作用下不同行驶速度对车桥动力响应的影响，对于不同烈度地震作用下车桥系统动力响应的研究相对较少。在输入地面激励时，一些研究只考虑地震波的作用，忽略了轨道随机不平顺的影响，轨道不平顺引起的列车振动会随着列车速度的提高成倍增大［6］，新近的研究表明，对地震作用下列车运行安全性分析不应忽略轨道随机不平顺的影响［7］。从目前研究现状来看，关于地震条件下车桥动态安全性能的研究还不够系统、深入和完善。有的局限于垂向动力学的分析［8］，有的对车辆模型和轮轨关系做了大量的简化，对地震与列车耦合作用考虑不全面［9］，为此需要进一步开展相关方面的研究工作。

本文在前人的研究基础上，建立了车辆-桥梁空间耦合动力学模型，在考虑地震激励的同时，还考虑了轨道随机不平顺的影响，使激励更加接近真实。采用新型显式积分法［10］求解系统动力学方程，分析了不同地震烈度对车辆运行平稳性的影响，可为地震作用下铁路桥梁的动力响应分析和车辆的运行安全分析提供参考。

1 地震作用下车辆-桥梁耦合系统分析模型

1.1 车辆空间振动分析模型

分析中，本文做如下假定：①车体、转向架和轮对均假定为刚体；②车体、转向架和轮对之间均作微振动；③弹簧假定为线性，阻尼按黏滞阻尼计算；④轮轨关系采用垂向密贴横向蠕滑线性简化模型［11］。图1为车辆-桥梁空间耦合系统模型，车辆采用四轴整车模型，车体和转向架考虑横移、沉浮、侧滚、摇头和点头5个自由度，轮对考虑横移、沉浮和侧滚3个自由度，整车共有27个自由度。

根据D′Alembert原理可以推导出车辆多刚体系统的动力学方程，可表示为如下矩阵形式，具体形式可参见文献［10］。

式中：[Mv]，[Cv]，[Kv]分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵，分别为车辆系统振动的加速度向量、速度向量和位移向量，{Fv} 为车辆系统激励列向量。

图1 车辆-桥梁空间耦合系统模型Fig.1 Model of spatial coupled system of train and bridge

1.2 桥梁空间振动分析模型

假设桥梁为等截面简支梁，质量均匀分布，考虑垂向、横向和扭转3个方向的自由度，桥梁的运动满足小变形理论并在弹性范围内，以垂向振动为例，其振动微分方程［12］可表示如下：

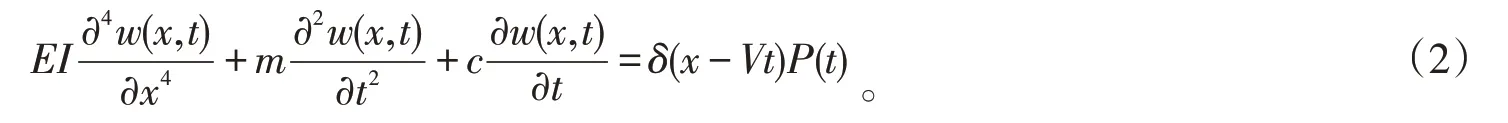
其中：δ为Dirac函数；P(t)为轮对作用在桥上的力。

对于等截面的简支梁，其振型函数可假定为三角函数

其中：n为桥梁的模态阶数。

引入广义振型坐标qn(t)，则桥梁的任一截面上垂向的运动可由振型函数叠加表示为

采用Ritz 法，将（4）代入（2）式并乘以第n阶振型函数φn(x)，再沿梁全长积分，并考虑振型的正交特性，即可将四阶偏微分方程转化为二阶常微分方程：

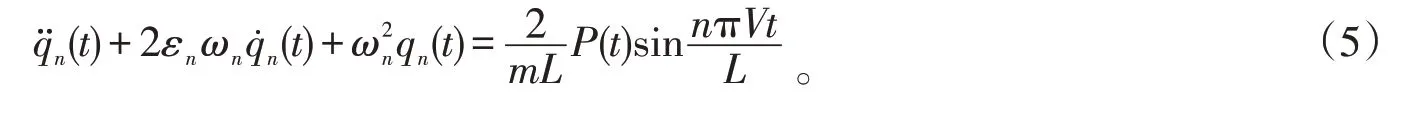
至此，得到了桥梁垂向振动微分方程。桥梁横向和扭转振动微分方程可类似得出［10］。

1.3 车桥耦合系统动力学分析模型

将车辆的动力学方程（1）和桥梁振型的广义坐标方程（5）进行组合，即可得车辆-桥梁耦合系统的动力学方程：

式中的下标v和b分别表示车辆和桥梁，其中

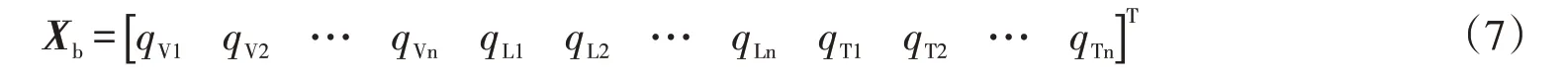
这里，qV，qL，qT分别为桥梁在垂向、横向和扭转方向的广义坐标。

地震作用下车桥系统分析模型是由车辆模型和桥梁模型组成的耦合系统，系统的激励源为轨道随机不平顺和地震的振动。地震作为外部激励作用在车辆和桥梁上［13］。地震作用下车桥耦合系统的动力学方程为

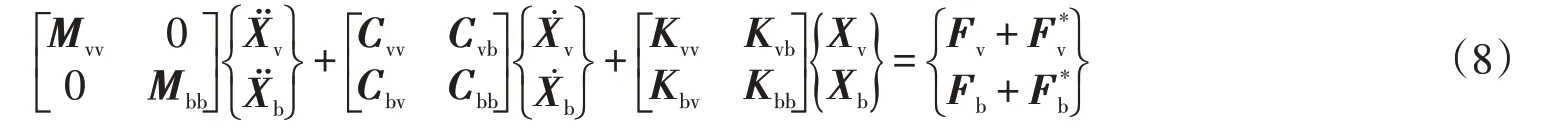
式中：Fv*，Fb*分别表示车辆和桥梁的地震力向量，篇幅所限，其它相关矩阵不详细罗列。

2 系统激励模型

2.1 轨道随机不平顺

轨道随机不平顺的统计特征只能依靠线路实地测量获得，迄今为止，我国尚未形成表征自己铁路线路状态的轨道谱标准，只有相关部门给出的一些建议的功率谱密度表达式。而国外对于轨道不平顺功率谱的研究已相当深入，并且形成了相应的轨道谱标准［10］；因此，在计算中选用了适用于高速铁路的德国高速轨道低干扰谱，其功率谱密度公式如下：

高低不平顺

方向不平顺

其中：Av，Aa是粗糙度常数；Ω为轨道不平顺的空间频率；Ωc，Ωr是截断频率。具体取值参见文献［10］。

通过数值模拟的方法［14］，将轨道随机不平顺功率谱密度函数转换为空间时域样本引入车桥耦合系统。

2.2 地震波的规格化

在分析地震作用下车辆-桥梁系统的动力响应时，通常选用一些国际上常用的真实地震加速度记录，进行规格化处理之后作为系统的输入激励。地震作为外部激励作用在车辆和桥梁上，采用一致激励模式，假定地震发生时基础各点以相同的振幅和相位振动，不考虑场地效应和地震波的行波效应，即每跨桥梁受到的地震作用相同。本文选用典型的El Centro地震波作为地震输入激励。

地震波的规格化是将实际地震记录的加速度峰值调整为分析需要的峰值，按照《建筑抗震设计规范》［15］的规定：当结构采用三维空间模型需要双向或三向地震波输入时，其加速度最大值通常按1（水平1）：0.85（水平2）：0.65（竖向）的比例调整。本文在计算时不考虑车辆和桥梁的纵向振动，因此采用双向输入，按最不利的情况考虑，即按1（水平1）：0.65（竖向）的比例调整，地震波的加速度最大值为

式中：ay(t)，az(t)和a′y(t)，a′z(t)分别为调整前后的地震波加速度，下标y，z分别表示水平和竖向。

根据《建筑抗震设计规范》给出的地震烈度和地震加速度峰值对应关系，如表1所示，将初始地震波进行规格化处理之后即可得到分析所需的地震波，表中g为重力加速度。

表1 地震烈度和加速度峰值对应关系Tab.1 Relationship between seismic intensity and maximum acceleration

3 数值计算方法

车桥耦合系统动力学模型可知，车桥耦合系统的动力学方程可表示为如下形式：

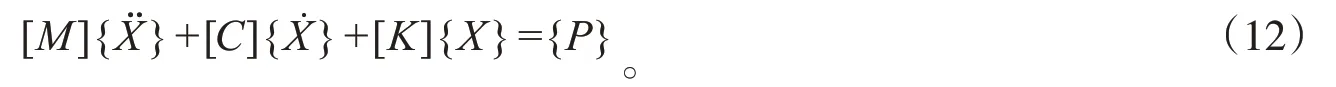
本文采用文献[10]提出的新型显式积分法进行数值求解。新型显式积分法是由Newmark 法演变而来的，其积分格式为

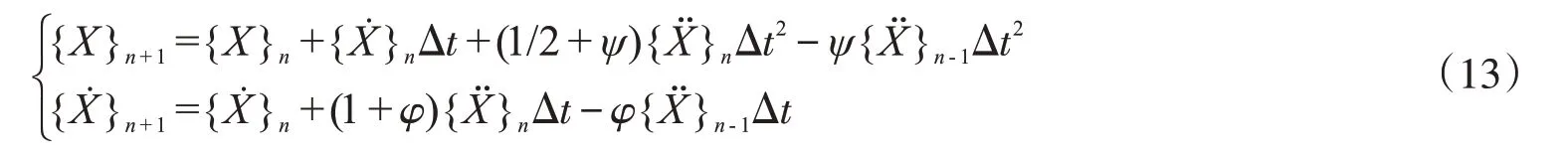
其中：φ，ψ为积分参数。将上式代入系统微分方程（12）在t=(n+1)Δt瞬时的形式

由上式可得

其中：

根据初始条件可得

于是便可按递推公式（13）及（15）逐次计算出各步长对应的位移、速度和加速度离散值。起步时只需令φ=ψ=0，从而使本方法具有积分“自开始”的特性。

4 车桥耦合系统动力响应分析

本文以高速铁路车辆-桥梁耦合系统为研究对象，其中车辆选用高速车辆模型，模型的具体参数详见文献［10］中的附表6，桥上轨道结构和桥梁视为一体，桥梁采用多跨单线高速铁路简支梁形式，桥梁的相关参数为：弹性模量Eb=2.943×1010N·m-2，桥梁横截面在两个方向的转动惯量分别为Ibz=8.78 m4、Iby=14.83 m4，每跨桥梁长度Lb=24 m，桥梁各阶阻尼比均为0.05。假设车辆以250 km·h-1的速度匀速运行于桥梁上，桥梁共有9跨。不考虑墩高对系统响应的影响，系统的振动位移从静平衡位置开始算起。采用新型显式积分法求解系统振动方程，取积分参数φ=ψ=1/2，时间步长Δt=200 μs。我国将地震烈度划分为12 个等级，6 度以下地震的加速度峰值较小，对车桥耦合系统的影响不大；桥梁的抗震设防烈度为9度，当地震烈度大于9度时桥梁可能已经发生破坏，故本文主要研究地震烈度为6～9度时车桥耦合系统的动力响应。

4.1 系统动力响应分析

根据表1不同烈度的地震所对应的加速度峰值将地震波进行规格化处理，引入车桥耦合系统，便可得到车桥耦合系统在地震作用下的动力响应，图2～图5为地震烈度为9度时桥梁的动力响应曲线。

图2 地震烈度9度时桥梁中点垂向加速度Fig.2 Vertical acceleration of the bridge midpoint under 9-degree of seismic intensity

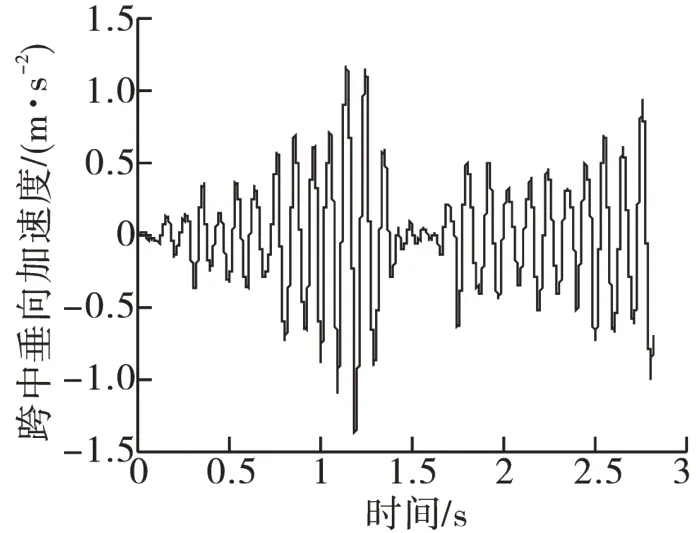
图3 地震烈度9度时桥梁中点横向加速度Fig.3 Horizontal acceleration of the bridge midpoint under 9-degree of seismic intensity

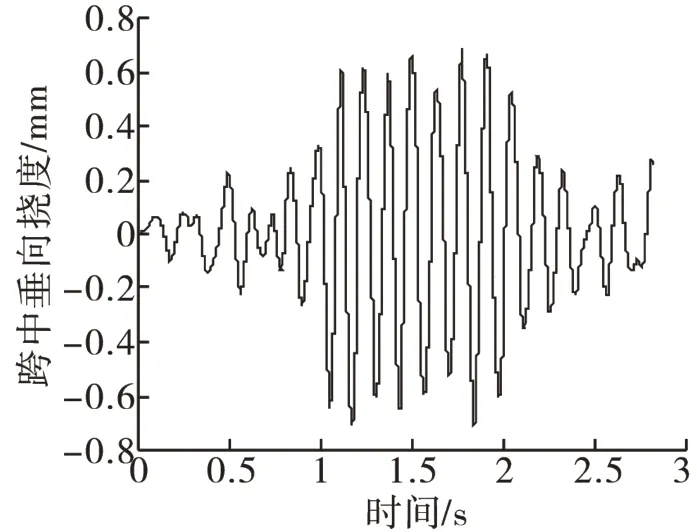
图4 地震烈度9度时桥梁中点垂向挠度Fig.4 Vertical deflection of the bridge midpoint under 9-degree of seismic intensity

图5 地震烈度9度时桥梁中点横向挠度Fig.5 Horizontal deflection of the bridge midpoint under 9-degree of seismic intensity

根据《高速铁路设计规范（试行）》［16］的规定：桥梁的垂向和横向振动加速度限值分别为0.50g和0.14g，g为重力加速度；桥梁的垂向挠度限值为L/1 400，横向挠度限值为L/4 000，L为桥梁跨度。由图2～图5可以看出：当地震烈度为9度时，桥梁垂向、横向的加速度和挠度均满足限值的要求。

对于高速铁路车辆，车体振动加速度的标准为：垂向振动加速度0.13g，横向振动加速度0.10g。表2为不同烈度地震作用下车体的振动加速度峰值，可以看出：当地震烈度为7度，地震加速度峰值为0.10g时，车辆的垂向和横向最大加速度的绝对值分别为0.23g和0.13g，已经大于车体振动加速度标准规定的0.13g和0.10g，车辆将不能平稳地运行于桥梁之上。

4.2 地震对车辆Sperling指标的影响

我国机车车辆运行平稳性指标采用Sperling指标，平稳性评定等级的限值为3.0［10］，Sperling指标计算公式为

式中：A为车体振动加速度；f为振动频率；F(f)为频率修正系数。具体取值参见文献［10］。

表2 不同烈度地震下车体振动加速度峰值Tab.2 Maximum acceleration of the vehicle under different degrees of seismic intensity

表3为不同烈度地震作用下车辆垂向和横向Sperling指标，可以看出：当地震烈度为8度，地震加速度峰值为0.3g时，车辆垂向Sperling 指标超出限值；当地震烈度为9 度，地震加速度峰值为0.4g时，车辆横向Sperling指标超出限值。

表3 不同烈度地震下车辆Sperling指标Tab.3 Sperling index of the vehicle under different degrees of seismic intensity

4.3 轨道随机不平顺的影响

为了考察轨道随机不平顺对地震作用下车桥耦合系统的影响，在一定烈度的地震作用下，对比不考虑随机不平顺和考虑随机不平顺情况下车桥耦合系统的动力响应。根据数值结果可知，轨道随机不平顺对车辆的垂向和横向加速度响应影响都非常小，对桥梁横向加速度响应的影响也不太明显，而对桥梁垂向加速度响应的影响相对明显。表4为不同烈度地震下桥梁垂向振动加速度的峰值，可以看出，随着地震烈度的增大，轨道随机不平顺对桥梁垂向振动加速度峰值的影响越来越小。因此，在相对较弱的地震作用下，如需详细研究桥梁的动力响应，需要考虑轨道随机不平顺的影响。

表4 不同烈度地震下桥梁垂向振动加速度峰值（m·s-2）Tab.4 Maximum vertical acceleration of the bridge under different degrees of seismic intensity

综上可知，车辆在地震烈度为7度时已经不能平稳地运行于桥梁上。车辆运行平稳性的Sperling指标相对加速度指标较为宽松，为了安全起见，采用相对保守的加速度指标更为合理。在相对较弱的地震作用下，轨道随机不平顺对桥梁的垂向加速度响应影响明显，分析时需要加以考虑。

5 结论

本文建立了车辆-桥梁耦合系统动力学模型，将规格化的地震波作为外界激励引入系统模型，同时考虑了轨道随机不平顺的影响，采用新型显式积分法对系统动力学方程进行求解，得到了车桥耦合系统在地震波和轨道随机不平顺共同作用下的动力响应，并且对不同烈度地震作用下车桥耦合系统的动力响应进行了分析。研究表明：

1）当地震烈度为9度及以下，地震加速度峰值不大于0.4g时，桥梁的垂向和横向振动加速度，垂向和横向挠度均满足《高速铁路设计规范（试行）》中规定的限值要求。

2）当地震烈度为7度，地震加速度峰值为0.10g时，车辆的垂向和横向加速度超出限值；当地震烈度为8度，地震加速度峰值为0.3g时，车辆运行平稳性的Sperling指标超出限值。

3）车辆运行平稳性的Sperling指标相对加速度指标较为宽松，为了安全起见，应当采用相对保守的加速度指标，当地震烈度为7度，地震加速度峰值为0.10g时，车辆已经不能平稳地运行于桥梁上。

4）在相对较弱的地震作用下，轨道随机不平顺对桥梁垂向加速度响应的影响明显，如需详细研究桥梁的动力响应，应当考虑轨道随机不平顺的影响。

[1]王开云,王少林,杨久川,等.地震环境下铁路轮轨动态安全性能及脱轨研究进展[J].地震工程与工程振动,2012,32(6):82-94.

[2]王少林,翟婉明.地震作用下高速列车-线路-桥梁系统动力响应[J].西南交通大学学报,2011,46(1):56-62.

[3]JU S H.Improvement of bridge structures to increase the safety of moving trains during earthquakes [J].Engineering Structures,2013,56:1563-1579.

[4]XIA C Y, XIA H, ROECK G De.Dynamic response of a train-bridge system under collision loads and running safety evaluation of high-speed trains[J].Computers and Structures,2014,140:23-28.

[5]陈水生,黄里.双柱式桥墩刚度对桥梁地震响应分析[J].华东交通大学学报,2014,31(3):29-34.

[6]房建,雷晓燕,练松良.轨道不平顺波长对桥上CRTS II 型板式轨道振动特性的影响[J].华东交通大学学报,2014,31(1):1-6.

[7]徐鹏.列车-轨道-路基耦合振动及地震条件下行车安全性分析[D].成都:西南交通大学,2012.

[8]LIU M F,CHANG T P,ZENG D Y.The interactive vibration behavior in a suspension bridge system under moving vehicle loads and vertical seismic excitations[J].Applied Mathematical Modelling,2011,35:398-411.

[9]陈令坤.地震作用下高速铁路列车-无砟轨道-桥梁系统动力响应及走行安全研究[D].长沙:中南大学,2012.

[10]翟婉明.车辆-轨道耦合动力学[M].3版.北京:科学出版社,2007.

[11]杜宪亭.强地震作用下大跨度桥梁空间动力效应及列车运行安全研究[D].北京:北京交通大学,2011.

[12]夏禾,张楠.车辆与结构动力相互作用[M].2版.北京:科学出版社,2005.

[13]张楠,夏禾.地震对多跨简支梁桥上列车运行安全的影响[J].世界地震工程,2001,17(4):93-99.

[14]陈果,翟婉明.铁路轨道不平顺随机过程的数值模拟[J].西南交通大学学报,1999,34(2):138-142.

[15]中华人民共和国住房和城乡建设部.GB 50011-2010.建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

[16]中华人民共和国铁道部.TB 10020-2009.高速铁路设计规范(试行)[S].北京:中华人民共和国铁道部,2009.