论数学模型的建立在高职高等数学教学中的应用
2015-11-22刘国发
刘国发
(河南水利与环境职业学院 河南郑州 450008)
论数学模型的建立在高职高等数学教学中的应用
刘国发
(河南水利与环境职业学院 河南郑州 450008)
数学建模是培养学生将数学理论联系实际的有效途径,高等数学中处处蕴含着数学建模的思想,针对高职院校学生的数学能力,应尊重学生的认知规律,在学习高等数学基础知识过程中渐进式地培养数学建模能力。
高职生 数学建模教学 途径
一、数学建模在高职高等数学教学中的作用
学习的目的全在于应用。在高等职业教育中,由于其明确的职业教育基本类型,确定了高等数学课程教学必须服务于专业知识的学习,其教学目标不仅是高等数学基础知识的学习,重要的是培养学生应用数学知识解决实际问题的意识和能力。解决实际问题,实质是综合运用知识的思维活动过程,然而学生的思维活动需要借助外界的某种环境因素的剌激作用,所以在数学教学过程中,需要创设适当的问题情境,以启动学生的思维机器,使学生在获得知识的过程中,增进理解知识的来源、发展技能,提高解决实际问题的能力。作为联系数学理论和实际问题的桥梁和纽带的数学建模,恰为实现提高解决实际问题的能力提供了有效途径。
二、数学建模在高职高等数学教学中应用坚持的原则
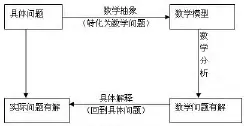
我们知道,数学模型就是用数学语言、方法表述实际问题,其目的是便于继续用数学的手段对其进行分析、处理,以便获得对实际问题更多的、不易观察出的深层次信息,这种表述就是一个数学模型,其过程就是数学建模。多年来,在高等院校中数学建模活动的开展,为大学生数学知识的应用、提高创新能力找到了一条行之有效的途径。然而,数学建模需要较扎实的数学功底和较宽泛的多学科知识,特别是数学建模竞赛,并非每个大学生都有能力完成。伴随着高等教育的大众化,高职院校学生的数学能力弱化、学习自觉性差是每位数学教师都不可回避的现实,他们的高中基础数学知识欠缺,更不具备用数学知识分析问题的意识和能力。因此,如何利用数学建模教学来提高学生解决实际问题的能力,是必须认真研究的高等数学教学方法。
首先,必须牢固树立“有数学就有数学建模”的教学理念。如“历史上影响人类生活的十大公式”之两例:原始公式——1+1=2,勾股定理——A2+B2=C2。这就促使教师在教学过程中有意识地引导学生充分认识数学现象,提高教师在教学过程中培养学生分析问题的意识。
其次,要明确数学建模的教学目标。要利用一些较简单的实际问题,强调分析过程,培养学生分析问题的能力。
第三,精选案例。毫无疑问,数学建模是高职学生不易掌握的学习内容。要结合学生的生活、专业特点,理论联系实际,培养学生的数学建模兴趣。
三、数学建模在学习高等数学基础知识过程中的应用
数学本身就是为了实际应用才产生的,它的很多重大发现都是从实际问题的需要面出现的。很多高等数学概念的建立,都有其自身的数学模型,而数学模型又有其背景材料,教学中应展示其产生和发展的过程,培养解决问题的意识,把握解决问题的一般程序:
案例一:变速直线运动的瞬时速度——建立导数概念
(2)问题的分析:物体自由下落,经过时间,所经过的路程为

当时间由t0变到t0+△时,物体所经过的路程为
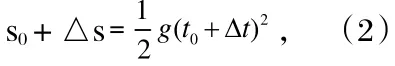
由式(2)-式(1)得物体在△时间内经过的路程
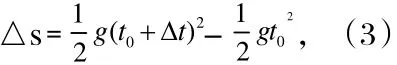
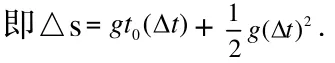
将式(3)两端同除以,得物体在时间内的平均速度,即
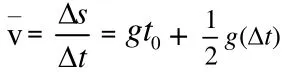
(3)设变量、符号说明:△t——物体从t0时刻后的时间增量,△s——物体在△t时间内的路程增量平均速度,v(t0)——t0时刻的瞬时速度。
(4)建立数学模型:根据对问题的分析,t0时刻的瞬时速度可表示为数学式
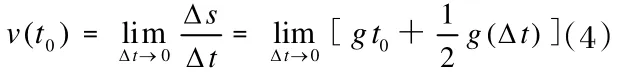
(5)模型的求解:对(4)求出极限,得时刻的瞬时速度

在高等数学基础知识的学习过程中,无不处处渗透着数学模型的思想。再如通过求曲边梯形的面积来建立定积分的概念,用无限分割的思想,加强用“微元”分析方法建立积分模型的过程,使学生对非均匀积累问题的数学建模有一个深刻印象。即采用“分割→近似→求和→取极限”四个步骤建立所求量的积分模型,可简记为
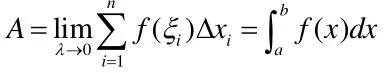
并用积分模型求不规则平面图形的面积、空间图形的体积、曲线弧长、液体压力、变力作功等。
通过在学习高等数学基础知识的过程中培养学生的数学建模思想,是从高职学生的基础知识实际出发来培养学生分析、解决实际问题的最基本途径。
四、精选案例,开阔思路
以高等数学基础知识为背景,选择难度较低的实际问题,通过建立数学模型,直接对数学知识加以应用。
案例二:变化率模型——导数的应用
表示自变量每改变一个单位时,函数y的平均变化率;当△x→0时,若y可导,则为函数y=f(x)的瞬时变化率。
(1)问题的提出:在离水面高度为H的岸上,用绳子拉船靠岸。假设绳子的长度为L,船位于离岸S处,那么,当收绳速度V0保持不变时,船的速度V是否改变?
(2)问题的分析:水面高度为H、绳子的长度L、船位于离岸的距离S构成了直角三角形,由勾股定理得
