深水钻井导管下深区间确定及风险评价方法
2015-11-22许玉强管志川张会增张洪宁隋修平
许玉强,管志川,王 庆,张会增,张洪宁,隋修平
(1.中国石油大学石油工程学院,山东青岛266580;2.山东交通学院海运学院,山东威海264200)
深水钻井导管下深区间确定及风险评价方法
许玉强1,管志川1,王 庆1,张会增1,张洪宁1,隋修平2
(1.中国石油大学石油工程学院,山东青岛266580;2.山东交通学院海运学院,山东威海264200)
深水钻井导管的下入深度直接关系到海底井口的力学稳定性及后续钻井作业的安全。通过分析,确定导管存在最小下深和极限下深,并给出极限下深计算模型。基于概率统计和地质统计学方法,将目标点邻井的承载力增长系数进行概率统计,并通过差值算法对目标点进行移植预测,得到该系数在目标点处含有概率信息的预测值,将导管最小下深由单值变为含概率信息的分布带,同时结合导管极限下深的概率化分布,对目标井的导管设计下深进行定量风险评价。实例分析表明:承载力增长系数这一区域经验变量对深水导管下深影响很大,尤其当取值较小时,导管下深随着该系数的减小呈指数增长;该方法在给定可信度条件下可计算导管绝对安全下深区间,有效避免了因承载力增长系数不确定等因素导致的导管下深风险。
深水钻井;导管下深;风险评价;承载力增长系数;下深范围;概率统计
深水钻井与浅海钻井最大的区别就在于水深较大,这就需要很长的隔水管来保证钻井作业的进行[1]。受钻井船漂移、海流冲击等问题影响,隔水管等会对海底井口的力学稳定性造成威胁[2-4]。近年来已有学者针对深水钻井中的隔水管受力状态、海底井口稳定性、海底泥线以下套管柱承载能力、导管下深等问题进行了研究,得出了一些有应用价值的结论[5-8]。其中深水钻井中导管的下入深度直接关系到海底井口的力学稳定性。若设计下入深度较浅,会导致海底井口失稳的发生;若设计下入深度较深,虽然保证了海底井口的安全,但会带来资源的浪费,甚至有可能导致导管无法下入到指定深度。同时深水海底浅部地层参数存在诸多不确定性,这给导管下深区间的精确计算带来了麻烦。目前的深水钻井导管下深设计存在一定的风险,须针对该问题建立一套风险评价方法。目前常用的深水钻井导管下深计算方法中涉及的主要变量包括:导管尺寸、管端阻力、恢复时间、承载力增长系数等,其中承载力增长系数是一个区域经验值,其取值存在较大的不确定性,这就影响了计算结果的可靠性;同时目前并没有计算导管极限下深的模型,导致无法判断导管能否下入到设计深度。基于概率统计和地质统计学[9]方法,可以将区域地层资料中的不确定性或难以确定的参数进行概率统计,并利用空间差值等数学方法对目标点的相关参数进行含概率信息的预测。笔者利用该方法对目标井的承载力增长系数进行分析,并结合深水导管下深计算方法确定导管最小下深,得到含有概率信息的导管最小下深分布带;同时通过建立分析导管极限下深模型,得到导管极限下深分布带,进而对导管下深的风险进行综合评价。
1 深水钻井导管最小下深和极限下深确定方法
目前深水钻井多采用水力喷射方式下入导管,因为深水浅部地层破裂压力低,若采用常规方式循环钻进易压漏地层,且该方式下入速度较快,有利于节约钻井成本。导管的下入深度主要与深水浅层土的性质及导管和后续套管等有关[10]。国内外学者对导管的下深计算已进行了较多的探讨[11],多是通过对导管悬挂表层套管后进行受力分析计算的下深,并没有考虑导管下入过程中能否下入到指定深度的问题。有必要计算导管的极限下深,以免现场作业时导管不能下到设计深度。
1.1 导管承载力计算
导管下入深度的确定与导管喷射下入过程的受力情况分不开,而且导管的承载力受时间效应的影响,目前考虑因素较为周全、计算结果较为准确的深水钻井导管承载力计算方法[11]如下。
导管的初始承载力为
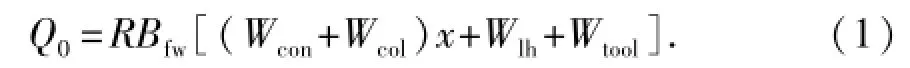
导管下入到位时悬挂表层套管后的承载力为
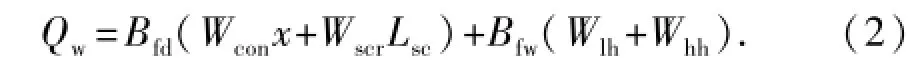
导管极限承载力为

导管实时承载力为
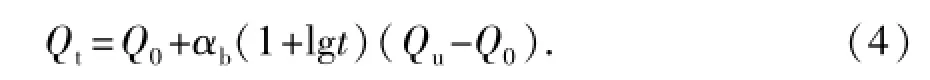
综合式(1)、(3)、(4)可得,导管下入后一定恢复时间的实时承载力为
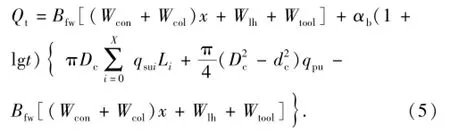
式中,Q0为导管的初始承载力,kN;R为钻压系数,取值为0.8~1.0;Bfw为海水中浮力系数;x为设计的导管长度,m;Wcon为导管线密度,kN/m;Wcol为喷射钻具线密度,kN/m;Wlh为低压井口重力,kN;Wtool为下入工具的重力,kN;Qw为导管下入到位时悬挂表层套管后的承载力,kN;Bfd为钻井液中的浮力系数;Wscr为表层套管线密度,kN/m;Lsc为表层套管下深,m;Whh为高压井口重力,kN;Dc为导管外径,m;dc为导管内径,m;qsui为导管周围第i层土的单位面积极限管侧阻力,kPa;qpu为单位面积极限管端阻力,kPa;Li为第i层土的厚度,m;X为土壤分层数;αb为承载力增长系数;t为恢复时间,d。
1.2 导管最小下深和极限下深确定方法
喷射下入导管过程中,施工最主要的控制参数是钻压,用以保证导管顺利下入到位的同时保持管串的垂直[12]。钻压控制要保证导管下入过程中管串的中性点在泥线以下,利用入泥管串的自身重力钻进[13]。同时,为了避免管串过分受压发生弯曲,且使导管到位后的承载力最大,要求导管最终到位时的钻压不得低于最大钻压的80%[12]。为了防止施工过程中导管串过分受压发生弯曲,只能靠入泥管串的自重进行钻进,从而导管的下深存在一定的极限,超过这个深度,便不能靠入泥管串的自身重力下入到位。
由于导管下入过程中喷射会对浅层土产生扰动,导致土壤试验测定的管端和管侧阻力不适用于刚下入到位时导管承载力的计算。根据相关文献对导管喷射钻进的数值模拟[14],水力喷射对周围土壤应力场产生的影响主要集中在喷嘴附近及其下方。在喷射钻进过程中,喷嘴附近土壤受冲击作用发生形变破坏,可以忽略导管下端一定范围内的管侧和管端阻力(由前人分析可知管端阻力对导管下深影响很小)。由此,导管在下入到极限下深时的承载力为
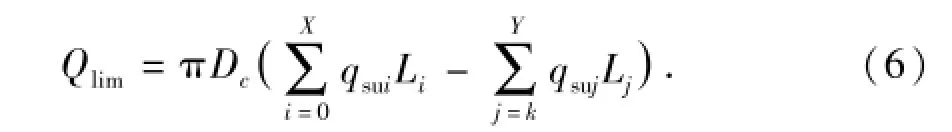
式中,qsui为受喷射影响的第j层土壤单位面积极限管侧阻力,kPa;Y为受喷射影响的土壤层数;Lj为导管外侧土壤受喷射影响较大区域的长度,m,其值与排量、导管到位时钻压、导管喷射钻具类型和喷射钻进速度等有关,它是由于喷射效应引起的土壤扰动还没有来得及恢复产生的,可由数值模拟结果求取。
根据力学平衡原理,导管下入到极限位置时应满足:
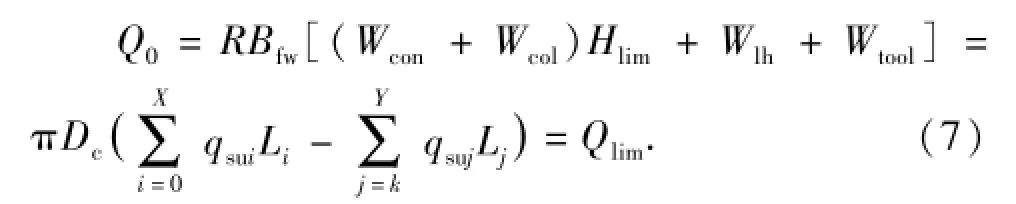
式中,Hlim为导管极限下深,m。
式(7)需要对Hlim进行迭代计算,可选取导管设计最小下深作为Hlim的初值。根据式(7)可以求得导管极限下深表达式为
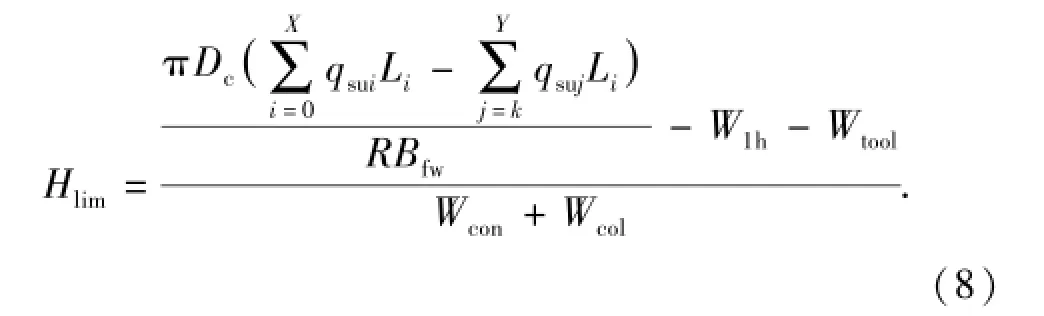
值得注意的是:此处计算的导管极限下深是以喷射下入过程中保持导管串中性点在泥线以下为原则计算的,该值是现场作业时依照设计钻压导管所能达到的最大下深。在实际钻进过程中,若在某一深度发生无法继续钻进的情况,一般可以采用上下活动管串、提高排量、加入膨润土钻井液等手段继续钻进,这样虽然使导管串下入更深,但会影响导管串的垂度,导致导管下入到位承载高压井口和表层套管等负重时,井口有失稳的风险。依照本文中方法计算得到的导管极限下深可以有效避免因设计不足导致的井口失稳风险。
导管最小下深须考虑时间效应,应满足一定恢复时间t后其承载力能承受导管和后续表层套管的总质量,即Qt≫Qw。为了便于计算,引入安全余量ε对其进行迭代计算,即

式中,εd为合理的安全余量下限值,kN;εu为合理的安全余量上限值,kN。
由此可计算出导管最小下深。
2 不同参数对导管下入深度影响
利用深水钻井导管最小下入深度计算模型,针对某深水区域[11]的导管下深进行分析,分别计算不同条件下的导管下深,分析各因素对导管下深的影响。
钻井设计参数如下:导管外径914.4 mm,壁厚38.1 mm,线密度7.8 kN/m,喷射钻具组合线密度3.6 kN/m,低压井口13.1×103kg,下入工具质量3.1×103kg,高压井口质量4.1×103kg,悬挂的表层套管柱850 m,线密度2.1 kN/m,水中浮力系数取0.85,钻井液中浮力系数取0.78,承载力增长系数取0.1,间隔时间t=2 d。地层相关参数见表1。
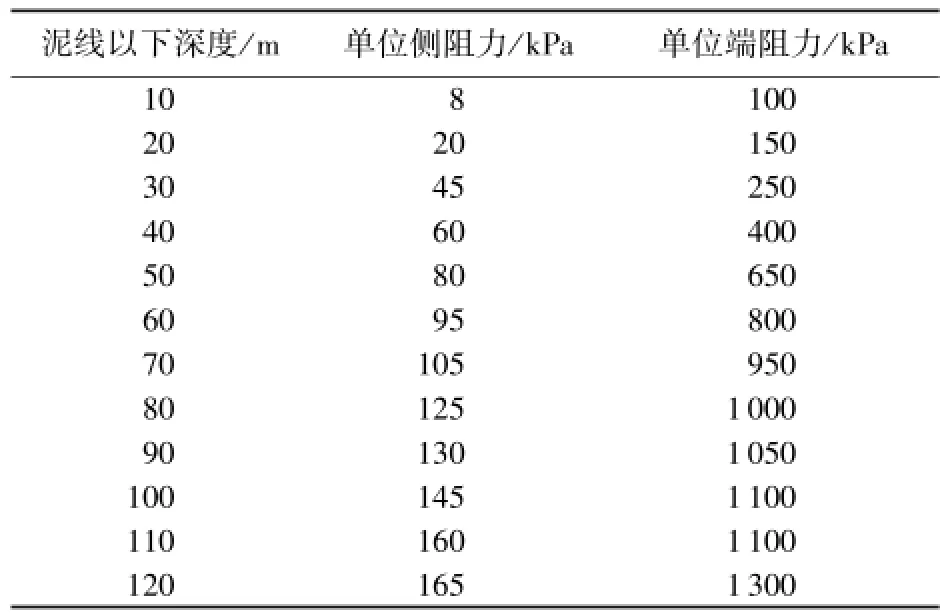
表1 周围土壤对导管串管端和管侧的阻力Table 1 Resistance of soil around conductor string on conductor's end and side
若设计安全余量下限εd为50 kN,上限εu为150 kN,则通过迭代计算出导管下深为75 m。
分别改变管端阻力、导管外径、恢复时间、承载力增长系数等,对导管下深重新进行计算。其中,考虑管端阻力时导管下入泥线以下深度为75 m,不考虑管端阻力时的导管入泥设计深度为78 m。具体计算结果如图1所示。
由以上计算结果可以看出,导管外径、管端阻力对导管下深影响很小;恢复时间小于2 d时,随着恢复时间的减少,其对导管下深影响变大,随着时间的延长,影响基本消失;承载力增长系数对导管下深影响很大,随着该系数的减小,导管下深基本呈指数增长。
从工程角度分析,恢复时间可以通过计算并结合工程需要进行精确控制,但承载力增长系数是一个区域性的经验值,具有不确定性,无法确定其精确值,它的细微的变化都会引起导管下深较大幅度变化,因此有必要对承载力增长系数进行合理预测。
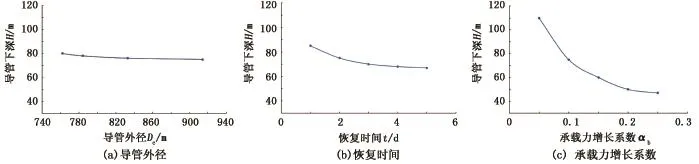
图1 不同参数对导管下深的影响Fig.1 Influence of different parameters on depth of conductor
3 承载力增长系数区域预测
承载力增长系数在一个区域内同时具有空间局限性、连续性、各向异性等特点,满足区域变量的特点,因此可以运用地质统计学理论对其进行区域预测[15]。
首先对该区域进行网格划分,采用正方形网格,如图2所示。其中δx、δy根据该区域的大小和数据点的数量进行合理取值,尽量使每个网格内均包含至少一个数据点。δz为网格厚度,由于承载力增长系数在纵向上无变化,可令δz=0,即进行平面网格划分。
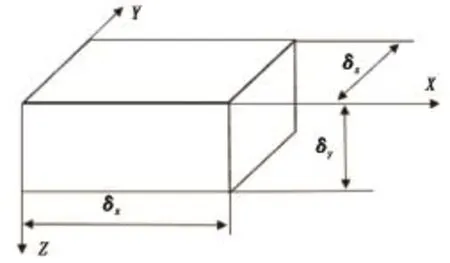
图2 区域网格划分示意图Fig.2 Schematic diagram of regional grid
假设该区域承载力增长系数的空间表达式为αi(xi,yi),其中i为已知数据点的编号,则每个网格的承载力增长系数为
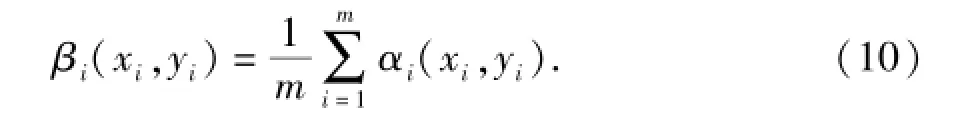
之后,进行变异函数的求取。本文中研究对象为平面区域参数,因此只介绍平面变异函数的求取。
令Ai代表平面坐标(xi,yi),d代表两个数据点所在网格中心的距离,则β(Ai)和β(Ai+d)分别代表区域参数在位置Ai和Ai+d上的数值,其中i=1,2,…,N(d),N(d)表示所在网格平面上分隔距离为d的网格总对数。根据变差函数的定义,计算变异函数的公式[16]为
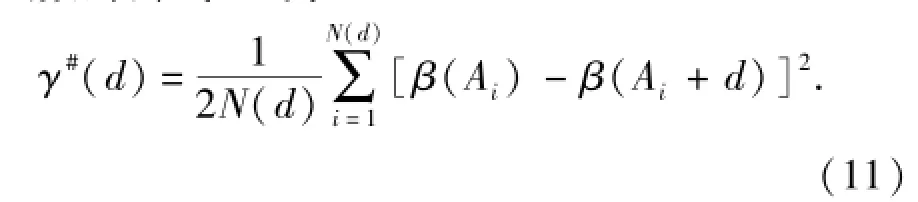
利用式(11)计算出不同间隔d条件下的变异函数值γ#(d),将其与常用的变异函数理论模型进行拟合或者套用。常用变异函数理论模型此处不再赘述。
根据克里格方法[17]可以得到目标点处承载力增长系数的带有概率信息的预测值:
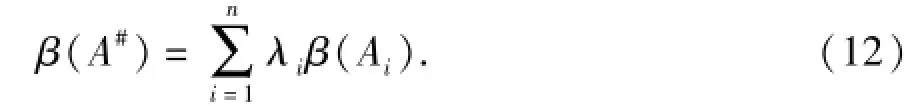
其中,λi可以通过求解克里格方程组得到:
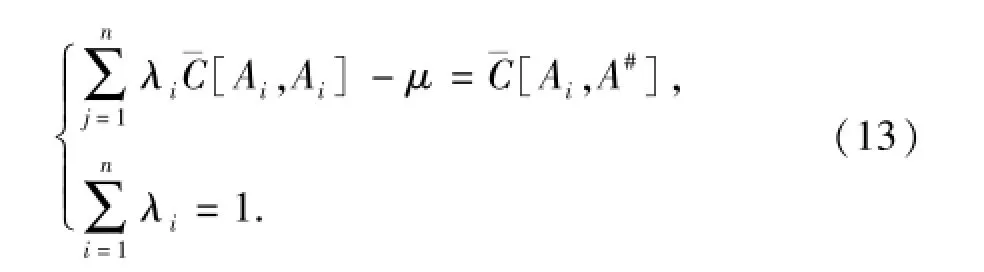
其中
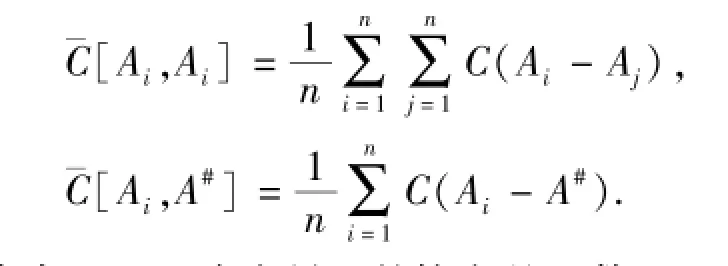
式中,C(x)为变量x的协方差函数。
对计算得到的目标点处承载力增长系数预测值求取方差,即
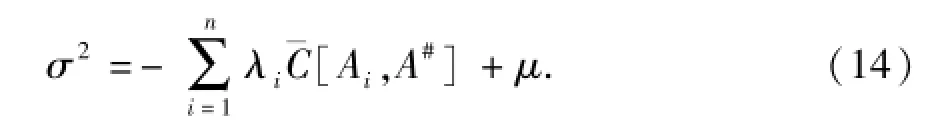
这样就得到了目标点处承载力增长系数的正态分布,其分布形式为N(β(A#),σ2)。
值得注意的是,该方法的计算精度取决于邻井资料的丰度,如已知井位的数量、间距和分布等。
4 深水钻井导管下深风险评价
根据建立的深水导管最小下深和极限下深的计算模型,通过对承载力增长系数的区域预测,可以将深水导管下深区间的边界实现概率化分布,设目标井处承载力增长系数的概率化分布形式为N(β(A#),σ2),如图3所示。求得导管最小下深的概率化分布形式如图4所示。
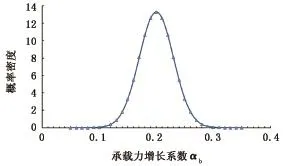
图3 目标井处承载力增长系数的概率化分布Fig.3 Probability distribution of bearing capacity growth coefficient of target well
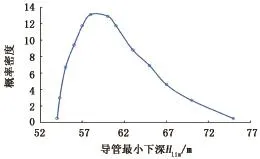
图4 导管最小下深概率化分布Fig.4 Probability distribution of the minimum depth of conductor
图4 中,导管最小下深的概率分布不再是对称形式,这是因为承载力增长系数对导管最小下深的影响为指数形式,一大一小两个相同概率的承载力增长系数,其中较小系数所对应的导管下深增大的更多。
式(8)为导管极限下深表达式。其中R为钻压系数,设计导管下深时取0.8~1.0,此时为一个固定值;但实际喷射钻进过程中,导管到位时的钻压受多因素的影响,实际值在一定合理范围内波动,因此在计算导管极限下深时R不能再取设计下深时的单一值,而是在该单一值附近波动。由此,设R的分布形式为N(R,σ2),其中R为设计导管下深时的钻压系数,σ依据设计钻压的波动范围进行确定。根据式(8)可以求得导管极限下深的概率化分布,如图5所示。

图5 导管极限下深概率化分布Fig.5 Probability distribution of ultimate depth of conductor
综合导管最小下深和极限下深概率化分布,可以便捷地确定一口井的导管设计下深所对应的风险概率,如图6所示。
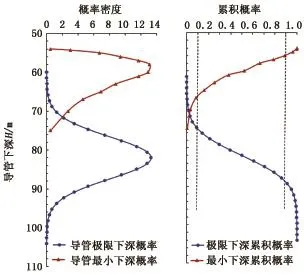
图6 导管最小下深和极限下深概率密度与累积概率分布Fig.6 Probability density and cumulative probability distribution of the minimum and ultimate depth of conductor
图6 中,可以根据导管设计下深确定对应的最小下深概率和极限下深概率,即导管承载力不足的概率和不能下入到位的概率。
为了方便计算一定可信度条件下的安全导管设计下深,将图6(a)中的概率密度转化为图6(b)的累积概率。由此,给定可信度J=J2-J1,即可评价导管设计下深的风险。
5 实例计算
以某深水区域DB-1为例,水深1 500 m,该区块已钻井位与目标井位分布如图7所示,认为每口已钻井所用的承载力增长系数是安全可靠的值,得到目标井处含有概率信息的承载力增长系数,该系数呈数学期望为0.175、标准偏差为0.03的正态分布形式。喷射钻进过程中钻压系数R取0.9。
计算目标井导管最小下深和极限下深的概率密度分布以及累积概率分布,如图8所示。
选取可信度J=J2-J1=90%-10%=80%,图8(b)中点B、C之间区域(67.5~75.2 m)即为80%可信度条件下的绝对安全导管下深;若导管设计下深处于点A、B之间区域(56.3~67.5 m),会一定程度上导致导管承载力不足,其具体发生的概率可由图8(a)求取;若导管设计下深处于点C、D之间区域(75.2~88.5 m),会一定程度上导致导管不能下入到位,其具体发生概率可由图8(a)求取。
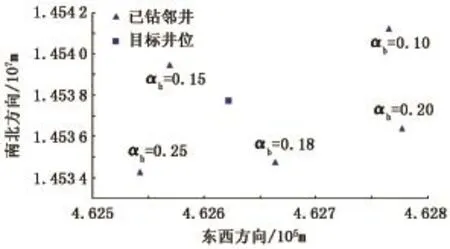
图7 井位分布Fig.7 Well location map
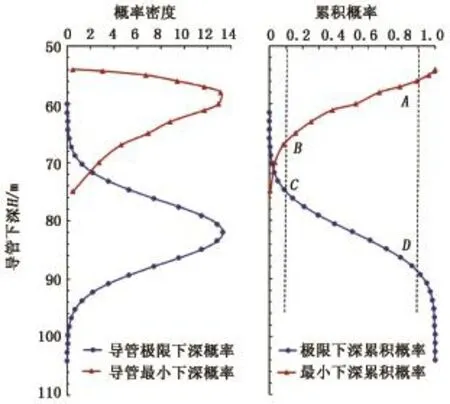
图8 目标井导管最小下深和极限下深的概率密度及累积概率分布Fig.8 Probability density and cumulative probability distribution of the minimum and ultimate depth of conductor of target well
6 结 论
(1)承载力增长系数这一区域经验变量对深水导管下深影响很大,尤其当取值较小时,导管下深随着该系数的减小呈指数增长。采用概率统计方法对目标井的承载力增长系数进行预测,得到含概率信息的预测值。
(2)建立了基于导管最小下深和极限下深概率化分布的导管下深风险评价方法,进一步引入累积概率分布和可信度,实现了对深水导管设计下深风险的定量评价。
[1] ROCHA L A S,JUNQUEIRA P,ROQUE J.Overcoming deep and ultra deepwater drilling challenges[R].OTC 15233,2003.
[2] SHAUGHNESSY J M,DAUGHERTY W T,GRAFF R L,et al.More ultra deepwater drilling problems[R]. SPE 105792,2007.
[3] 弓大为.海洋隔水管故障分析[J].石油矿场机械,2003,32(5):4-7. GONG Dawei.Analysis of marine riser failure[J].Oil Field Equipment,2003,32(5):4-7.
[4] 鞠少栋,畅元江,陈国明,等.深水钻井隔水管连接作业窗口分析[J].石油勘探与开发,2012,39(1):105-110. JU Shaodong,CHANG Yuanjiang,CHEN Guoming,et al.Envelopes for connected operation of the deepwater drilling riser[J].Petroleum Exploration&Development,2012,39(1):105-110.
[5] 刘彩虹,杨进,曹式敬,等.海洋深水钻井隔水管力学特性分析[J].石油钻采工艺,2008,30(2):28-31. LIU Caihong,YANG Jin,CAO Shijing,et al.Drilling riser mechanical characteristic of marine deepwater[J]. Oil Drilling&Production Technology,2008,30(2):28-31.
[6] 王鹏,闫铁,刘珊珊,等.深水隔水管与钻柱耦合作用力学模型[J].石油天然气学报,2014,36(6):83-86. WANG Peng,YAN Tie,LIU Shanshan,et al.Mechanical model of the coupling of deep water riser and drilling string[J].Journal of Oil and Gas Technology,2014,36(6):83-86.
[7] 刘秀全,陈国明,畅元江,等.台风条件下深水钻井隔水管触底事故分析及对策[J].石油勘探与开发,2013,40(6):738-742. LIU Xiuquan,CHEN Guoming,CHANG Yuanjiang,et al.Analyses and countermeasures of deepwater drilling riser grounding accidents under typhoon conditions[J]. Petroleum Exploration&Development,2013,40(6):738-742.
[8] 管志川,苏堪华,苏义脑.深水钻井导管和表层套管横向承载能力分析[J].石油学报,2009,30(2):285-290. GUAN Zhichuan,SU Kanhua,SU Yinao.Analysis on lateral load-bearing capacity of conductor and surface casing for deepwater drilling[J].Acta Petrolei Sinica,2009,30(2):285-290.
[9] 柯珂,管志川,周行.深水探井钻前含可信度的地层孔隙压力确立方法[J].中国石油大学学报(自然科学版),2009,33(5):61-67. KE Ke,GUAN Zhichuan,ZHOU Hang.An approach to determining pre-drilling formation pore pressure with credibility for deep water exploration wells[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33(5):61-67.
[10] 徐荣强,陈建兵,刘正礼,等.喷射导管技术在深水钻井作业中的应用[J].石油钻探技术,2007,35(3):19-22. XU Rongqiang,CHEN Jianbing,LIU Zhengli,et al. The application of jetting technology in deepwater drilling[J].Petroleum Drilling Techniques,2007,35(3):19-22.
[11] 苏堪华.深水钻井井口力学分析及导管承载能力研究[D].青岛:中国石油大学,2009. SU Kanhua.Analysis on mechanical stability of subsea wellhead and bearing capacity of conductor for deepwater drilling[D].Qingdao:China University of Petroluem,2009.
[12] AKERS T J.Jetting of structural casing in deepwater environments:job design and operational practices[J]. SPE Drilling&Completion,2008,23(1):29-40.
[13] 张辉,高德利,唐海雄.喷射安装导管作业中喷射管串力学分析[J].西南石油大学学报(自然科学版),2009,31(6):148-151. ZHANG Hui,GAO Deli,TANG Haixiong.Mechanics analysis of jetting string during jetting operation of conductor[J].Journal of Southwest Petroleum University(Science&Technology Edition),2009,31(6):148-151.
[14] 汪顺文,杨进,严德,等.深水表层导管喷射钻进机理研究[J].石油天然气学报,2012,34(8):157-160. WANG Shunwen,YANG Jin,YAN De,et al.Study on mechanism of deep surface water jet drilling[J].Journal of Oil and Gas Technology,2012,34(8):157-160.
[15] 管志川,柯珂,路保平.压力不确定条件下套管层次及下深确定方法[J].中国石油大学学报(自然科学版),2009,33(4):71-75. GUAN Zhichuan,KE Ke,LU Baoping.An approach to casing program design with formation pressure uncertainties[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33(4):71-75.
[16] 张仁驿.空间变异理论及应用[M].北京:科学出版社,2005.
[17] RUSSO D,BOUTON M.Statistical analysis of spatial variability in unsaturated flow parameters[J].Water Resources Research,1992,28(7):1911-1925.
(编辑 李志芬)
Determination and risk assessment methods for setting depth of conductor during deepwater drilling
XU Yuqiang1,GUAN Zhichuan1,WANG Qing1,ZHANG Huizeng1,ZHANG Hongning1,SUI Xiuping2
(1.School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China;2.Marine College,Shandong Jiaotong University,Weihai 264200,China)
The penetration or setting depth of conductor pipe can directly affect the mechanical stability of subsea wellhead and the safety of subsequent drilling operations.There should be a minimal setting depth and a limit setting depth,and a mathematical model for calculating the limit setting depth can be established.In this paper,probability statistics and geo-statistics methods were used for the assessment of the bearing capacity of the target point based on the data from adjacent wells. The bearing capacity growth factor of the target point can be predicted using a differential arithmetic method,in which the statistics information was included.Therefore,a distribution range for the minimal setting depth of the conductor pipe can be determined using the statistics data,and by combining its limit setting depth data,a quantitative risk assessment can be carried out for the conductor's setting depth.Case studies show that the bearing capacity growth factor is a regional and empirical variable that has a great impact on the setting depth of deepwater conductor,and the setting depth of conductor grows exponentially with the decrease of the growth factor,especially when its value is small.This method can calculate an absolute safe range for conductor's setting depth under the conditions of a given confidence,which can effectively avoid the risks caused by uncertainties of the bearing capacity growth factor and other factors.
deepwater drilling;conductor setting depth;risk assessment;bearing capacity growth factor;setting depth range;probability statistics
TE 22
A
许玉强,管志川,王庆,等.深水钻井导管下深区间确定及风险评价方法[J].中国石油大学学报(自然科学版),2015,39(6):85-91.
XU Yuqiang,GUAN Zhichuan,WANG Qing,et al.Determination and risk assessment methods for setting depth of conductor during deepwater drilling[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(6):85-91.
1673-5005(2015)06-0085-07
10.3969/j.issn.1673-5005.2015.06.011
2014-12-26
国家自然科学基金项目(51574275);国家“973”重点基础研究发展计划(2010CB226706);教育部“长江学者和创新团队发展计划”项目(IRT1086)
许玉强(1987-),男,博士研究生,研究方向为井下信息与控制、深水钻井及风险评价。E-mail:auyuqiang@163.com。
