动态连续潮流与改进细菌觅食算法结合的静态电压稳定裕度计算方法
2015-11-21薛英杰薛少飞
薛英杰,薛少飞
(1.太原理工大学,太原 030024;2.国网山西省电力公司检修分公司,太原 030032)
0 引言
近年来,电力系统向大电网、大机组、远距离、高电压的方向不断发展,系统日益复杂,对稳定性的要求也越来越高,其中电压稳定性是研究电力系统安全稳定运行的重要内容之一。自20世纪70年代以来,各国电力系统发生过多次电压稳定性问题,甚至造成电压崩溃的严重事故。电压崩溃不但造成巨大的经济损失,也给电力供应安全带来严峻挑战。因此,研究电力系统电压稳定性分析方法,寻找最优控制变量组合,提高系统的电压稳定性具有重要意义。
在静态电压稳定分析中,功率极限点被作为电压稳定的临界状态[1-2],是考核电压稳定性的重要指标。但由于在该极限点处,雅克比矩阵奇异,常规潮流很难收敛并求解。有文献[3-4]针对此问题提出的动态连续潮流模型(Dynamic Continuous Power Flow,DCPF)得到了广泛重视和应用,逐步成为电力系统静态电压稳定分析的主流工具。在动态连续潮流模型的基础上,为快速、准确寻找最优控制变量组合,各种以优化目标函数为目的的智能算法也作为寻优工具得到应用,如粒子群算法、沿途捕鱼算法、改进捕鱼算法等。以下提出改进细菌觅食算法并作为寻优工具[5-8],在连续潮流模型的基础上,分析计算电力系统静态稳定问题。
1 动态连续潮流模型
1.1 静态电压稳定裕度
静态电压稳定裕度指当前运行点负荷与电压崩溃点负荷之间的距离,可作为度量当前电力系统电压稳定水平的一个性能指标,简称裕度指标。一般是以可额外传输的负荷功率来表示的,因此又称为负荷裕度。如图1所示,鞍结分差点(SNB点)所对应的负荷即为稳定裕度λmax。
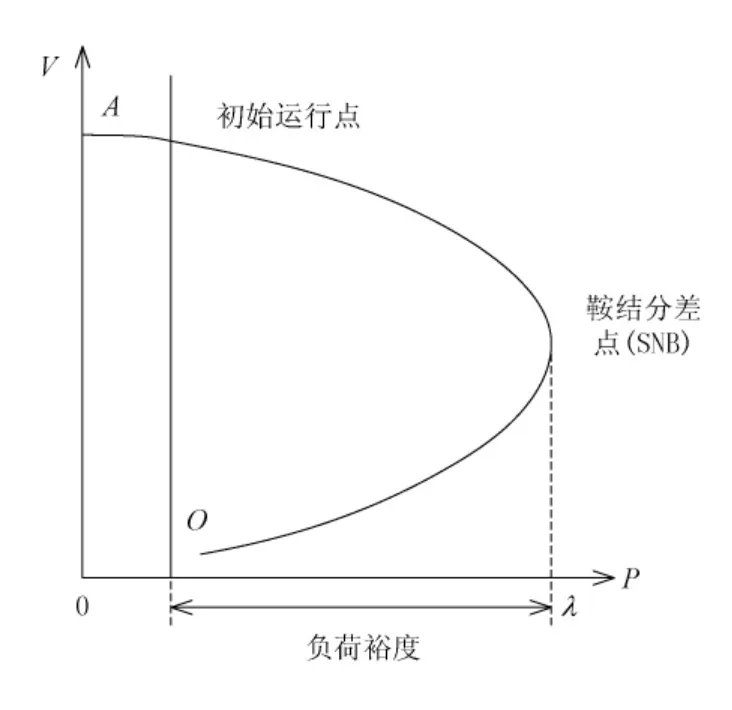
图1 静态电压稳定裕度示意
1.2 动态连续潮流模型
动态连续潮流数学模型如式(1)所示[9]。
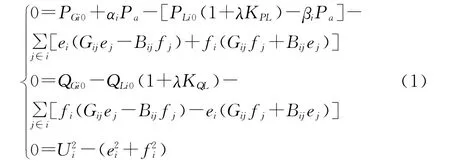
式中:Gij,Bij为节点导纳矩阵的实部和虚部;ei,fi为节点电压的实部和虚部;λ为引入的连续负荷参数,0≤λ≤λcr,当λ=0时,对应基态下发电机有功出力和负荷情况,当λ=λcr时,对应极限点发电机有功出力和负荷情况;PGi0,PLi0分别为基态下节点发电机与负荷的有功功率;QGi0,QLi0分别为基态下节点发电机与负荷的无功功率;KPL,KQL分别为负荷增加时负荷节点的有功、无功增长系数。当以恒功率方式增长时,KPL=KQL,如式(2)所示:

设αi,βi分别为各节点发电机和负荷分担的系统有功不平衡功率的分担系数,如式(3)所示:
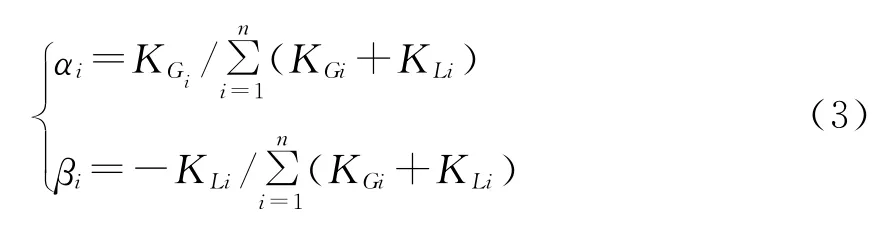
Pa为系统有功不平衡功率,如式(4)所示:
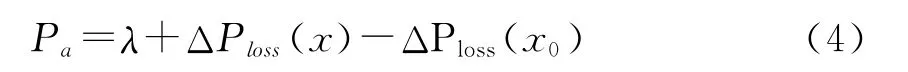
动态连续潮流与连续潮流所需求解的未知数个数相同,平衡节点的有功方程并不参加迭代,其求解过程类似于连续潮流。不同的是因为引入了网损增量,将原雅克比矩阵的稀疏性破坏。为了继续利用原潮流雅克比矩阵的稀疏性,该文采用了直接修正有功失配量法,即把第i-1步的网损增量看作是第i步的网损增量,如式(5)所示。这样修改,不会增加雅克比矩阵的非零元素,并能维持雅克比矩阵的稀疏性。
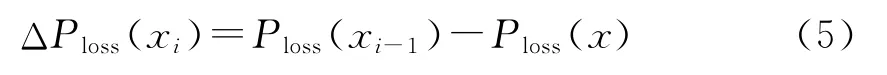
1.3 状态变量的优化模型
求解迭代过程中,当发电机无功出力越限或者PQ 节点电压越限时涉及节点转化问题,这将会增加迭代计算的难度,增加计算时间。引入精确罚函数法可以有效解决这个问题[9],其目标函数为:
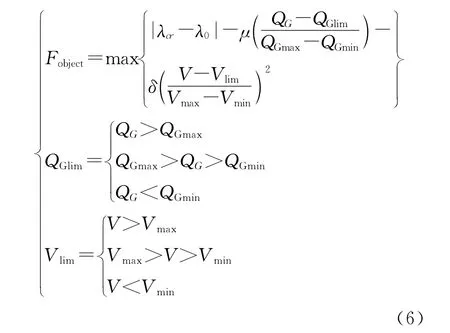
式中:Q为发电机节点无功功率;V为PQ 节点电压值;μ,δ分别为对应变量的惩罚函数。
2 细菌觅食算法及其改进
细菌觅食算法(Bacterial Foraging Algorithm,BFA)是通过对人体内大肠杆菌的觅食行为进行仿生学研究而得出的算法。相较于其他广泛用于优化问题的算法(例如,遗传算法,粒子群算法等)具有群体智能算法并行搜索、易跳出局部极小值等优点,受到了学术界的广泛关注。目前,细菌觅食算法已经被广泛应用于最优控制、滤波器优化设计、人工神经网络和工业生产调度[9-10]等多个领域。
2.1 基本细菌觅食算法
细菌觅食算法主要包括如下3个主要的计算操作步骤:
a.趋向性操作:在一个Dn的范围内,细菌随机旋转,选定一个方向,向最优解的方向行进,当所有鞭毛逆时针转动时,细菌向前游动;当所有鞭毛顺时针转动时,细菌原位置旋转。细菌就是靠这种机制来搜索最优位置的可能位置。细菌每进行一次趋向操作都按照下面公式来进行:
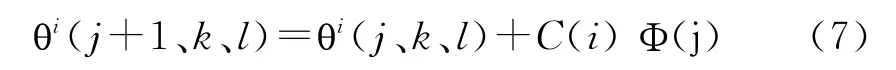
式中:C(i)表示向前游动的单位步长,大于零;Φ(j)表示旋转后选择的一个随机前进的方向。趋向性操作的流程如图2所示。
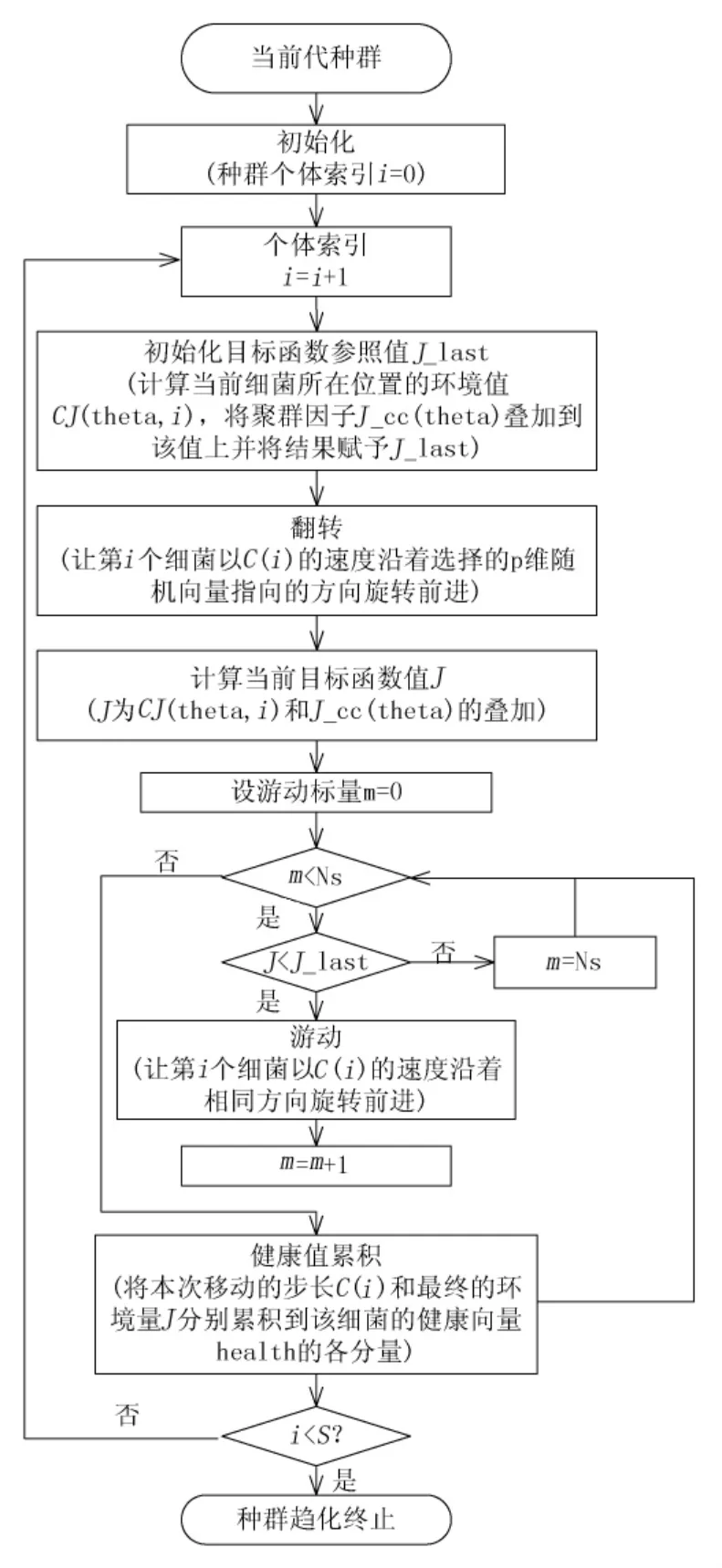
图2 趋向性操作流程
b.复制操作:设细菌总的数量为N,Fi(j,k,l)为个体i的适应度值,按照优胜劣汰的规则,依照适应度值的好坏对细菌进行排序,将坏的部分淘汰,剩余的好的部分进行复制,保证总体数量不变,同时保留了优秀的搜索能力。
c.迁徙操作:当细菌的生存环境发生了突变导致细菌不适应生存,则细菌会大量死亡,或者按照一定概率Ped迁徙。当细菌满足迁徙概率,则本体消亡,在区域内随机位置生成一个新的细菌,继续寻找最优位置,从而有利于跳出局部最优。
2.2 改进细菌觅食算法
改进细菌觅食算法(Improved Bacterial Foraging Algorithm,IBFA)是对现有算法的微观行为层面、基因改进层面和宏观指导层面进行改进,即将BFA 的3重循环改成先迭代后复制再迭代的过程,以提高BFO 基本算法的测试性能,并使之具备协调进化和学习适应等多重智能,从而达到提高算法的搜索速度和精度的目的。改进细菌觅食的流程如图3所示。
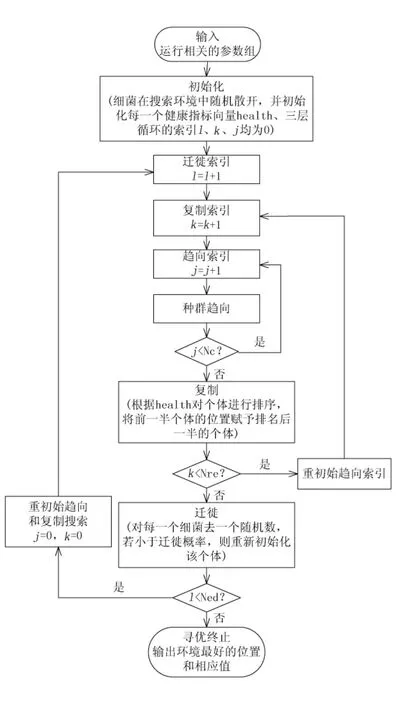
图3 改进细菌觅食算法流程
3 算例分析
使用改进细菌觅食算法,结合动态连续潮流模型,对静态电压稳定分析中的控制变量进行优化,并在IEEE 30 节 点 系 统 下 进 行 算 例 分 析[10],对比粒子群算法(PSO)控制变量最优组合寻找结果,验证细菌觅食算法的可行性及优化性能。
3.1 参数设置
改进细菌觅食算法参数设置为:搜索范围维度P=40(控制变量数组),细菌总个数S=60,趋向次数NC=14。趋向操作中,单向运动最大步数NS=5,复制次数Nre=6,迁徙次数Ned=17,细菌迁徙概率Ped=0.2,最大迭代350次。
细菌觅食位置θi对应静态电压稳定分析的控制变量的取值,即发电机端电压VGi,有载调压变压器的变比Ti,无功补偿装置投入的补偿容量QCi。在IEEE 30节点系统中,PV 节点有5个,有载调压变压器有4 个,无功补偿装置有2 个,所以,细菌所在位置表示方法与前述类同,只在对应的部分增加个数。
3.2 计算结果
在MATLAB 环境下,对IEEE 30标准节点系统进行编程和仿真。对DCPF 与PSO 结合、DCPF与IBFA 结合进行了计算,结果如表1、表2所示。
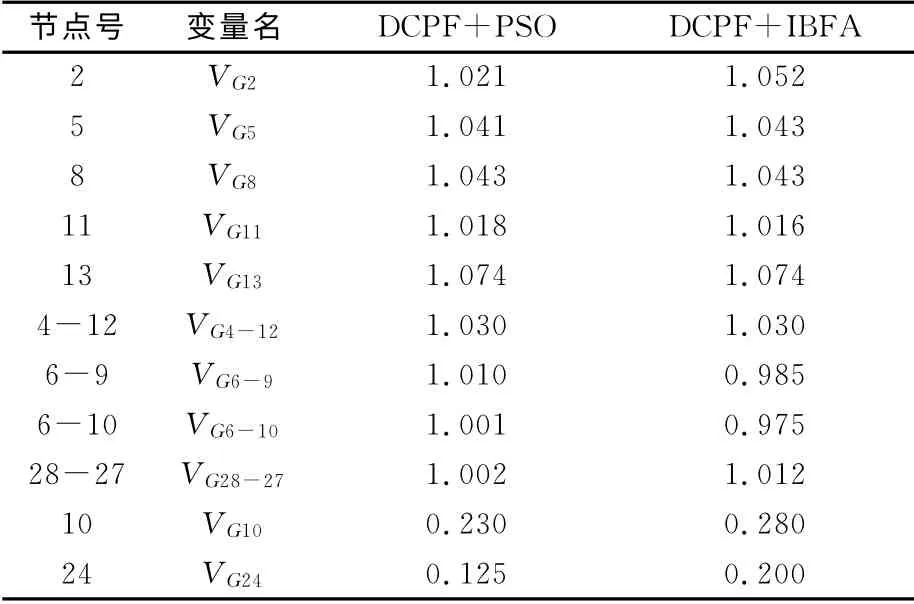
表1 IEEE 30节点系统控制变量最优组合

表2 IEEE 30节点系统的最大静态电压稳定裕度
由表1、表2计算结果可知,经过细菌觅食算法寻优得到的计算结果比粒子群算法得到的计算结果有明显的改进。
4 结论
以上采用DCPF结合IBFA 对系统的静态电压稳定裕度进行计算,并通过算例分析验证了所提算法的可行性。细菌觅食算法独有的趋向性操作使得算法具有较优的全局搜索能力;复制操作的精英保留机制赋予了种群优势团体获得越来越多的寻找最优解的机会,使其效率提高;迁徙操作也使得算法容易跳出局部最优,增加了在更大的范围内找到最优解的可能性。
[1]吴政球,李日波,钟 浩,等.电力系统静态电压稳定极限及裕度计算综述[J].电力系统及其自动化学报,2010,22(1):126-132.
[2]文学鸿,袁 越,鞠 平.静态电压稳定负荷裕度分析方法比较[J].电力自动化设备,2008,28(5):59-62.
[3]孙宏斌,李 钦,张明晔,等.基于动态潮流方程的连续潮流模型与方法[J].中国电机工程学报,2011,31(7):77-82.
[4]李 娟,薄明明,赵迎春,等.动态连续潮流与自适应混沌粒子群结合计算静态电压稳定裕度[J].电工电能新技术,2014,33(1):36-41.
[5]戴秋萍,马 良,郗 莹.连续优化问题的细菌觅食改进算法[J].上海理工大学学报,2013,35(2):103-106.
[6]徐 鑫.细菌觅食算法研究[D].吉林:吉林大学,2012
[7]杨大炼,李学军,蒋玲莉.一种细菌觅食算法的改进及其应用[J].计算机工程与应用,2012,48(13):31-34,93.
[8]M.Senthil Kumar,Dr.P.Renuga.Bacterial Foraging Algorithm based Enhancement of Voltage Profile and Minimization of Losses Using Thyristor Controlled Series Capacitor(TCSC)[J].International Journal of Computer Applications,2010,7(2):21-27.
[9]刘小龙.细菌觅食优化算法的改进及应用[D].广东:华南理工大学,2011.
[10]周雅兰.细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21.
