EVOLUTION FILTRATION PROBLEMS WITH SEAWATER INTRUSION:TWO-PHASE FLOW DUAL MIXED VARIATIONAL ANALYSIS∗

Gonzalo ALDUNCIN

Instituto de Geof´ısica，Universidad Nacional Aut´onoma de M´exico，M´exico，C.P.04510，Mexico

EVOLUTION FILTRATION PROBLEMS WITH SEAWATER INTRUSION:TWO-PHASE FLOW DUAL MIXED VARIATIONAL ANALYSIS∗

Gonzalo ALDUNCIN

Instituto de Geof´ısica，Universidad Nacional Aut´onoma de M´exico，M´exico，C.P.04510，Mexico

Tow-phase flow mixed variational formulations of evolution filtration problems with seawater intrusion are analyzed.A dual mixed fractional flow velocity-pressure model is considered with an air-fresh water and a fresh water-seawater characterization.For analysis and computational purposes，spatial decompositions based on nonoverlapping multidomains，above and below the sea level，are variationally introduced with internal boundary fluxes dualized as weak transmission constraints.Further，parallel augmented and exactly penalized duality algorithms，and proximation semi-implicit time marching schemes，are established and analyzed.

two-phase flow in coastal aquifers；fractional two-phase flow；dual mixed variational analysis；macro-hybrid variational formulations；augmented exactly penalized duality algorithms；proximation semi-implicit time marching schemes 2010 MR Subject Classification 35A15；47H05；35J50；76S05；35R35

1 Introduction

The purpose of this paper is to formulate and analyze variational two-phase flows in open coastal aquifers.For the physical model，we adopt the fractional two-phase dual mixed model of Chen and Ewing［1，2］，with an air-fresh water and a fresh water-seawater characterization，assuming the fresh water velocity as the wetting phase velocity.This mixed flow model corresponds to an instantaneous total velocity-global pressure incompressible flow，coupled with an evolution wetting velocity-complementary pressure compressible-like flow.Importantly，such a dual mixed two-phase flow modeling is appropriate for the application of composition duality methods［3，4］，in the solvability analysis of the system via duality principles.For analysis and computational purposes，suitable spatial decompositions，based on nonoverlapping multidomains，above and below the sea level，were variationally introduced with internal boundary fluxes dualized as weak transmission macro-hybrid constraints［5-7］.We should emphasize that these decomposed reformulations lead to macro-hybrid mixed localized models，which are veryappropriate for internal variational finite dimensional approximations，implementable in terms of non-matching finite element discretizations［8，9］.

∗Received November 11，2013；revised February 14，2015.The work reported here is part of a project partially supported by DGAPA，UNAM:PAPIIT Clave IN100214.

Further，parallel augmented and exactly penalized duality algorithms，as well as proximation semi-implicit time marching schemes of the Douglas-Rachford and Peaceman-Rachford type，are established and analyzed.

In a recent study［10］，we considered this evolution filtration problem in the sense of a slightly compressible Darcian velocity-pressure mixed single phase flow，which corresponds to a mixed variational approach of the classical variational pressure model presented in［11］.Such a classical pressure model was in turn an extension to general domains with seawater intrusion，of evolution filtration problems based on the pioneer Baiochi's transform analysis［12］；see［13-17］. In this paper，our interest is to apply a special two-phase approach to the evolution coastal filtration problem，in conjunction with a natural compositional duality macro-hybrid mixed variational analysis.

2 Physical and Mixed Variational Models

In this section，we start with a qualitative description of the open coastal aquifer to be considered，and the definition of its two-phase flow model.Corresponding mixed variational formulations are established through composition duality methods，and their solvability analysis is performed via duality principles.

2.1 The Qualitative Mixed Physical Model

Let Ω⊂ℜ3denote the spatial configuration of a coastal aquifer，a bounded connected domain with a Lipschitz continuous boundary∂Ω.We shall consider the following partition of boundary∂Ω（Figure 1）:Hence，assuming immobile seawater phase，our interest is to determine and analyze the evolution of the fresh water flow in the wet set Λ⊂Q=Ω×（0，T），for arbitrary and fixed T∈（0，+∞），whose boundary∂Λ⊂∂Q=∂Ω×（0，T），relative to∂Ω，has the corresponding partition

Fig.1 A section of an open coastal aquifer

For an incompressible flow process through the porous media，let ρfand ρsbe constant parameters denoting the fresh water and seawater mass densities，ρs＞ρf＞0，and define ρ≡1-ρs/ρf＜0.Further，let︿h∈｛︿h1，︿h2，···，︿hnr｝denote the time-varying fresh water ordinate levels for the nrreservoirs of the hydraulic system，relative to the fixed sea level as the origin（y=0）.Also，following［10］，in order to guarantee that the seawater intrusion cannot be in contact with the fresh water reservoirs，and that the（possibly empty）impervious flow boundary Σi=∂Λ∩∂Ωibe geometrically vertical，we introduce the conditions

Consequently，the coastal aquifer flow domain is characterized by

where Λ+=［p=0］≡｛（x，y，z，t）∈Q:p（x，y，z，t）=0｝，Λ=［p＞ϕ］≡｛（x，y，z，t）∈Q: p（x，y，z，t）＞ϕ｝and Λ-=［p=（ρ-1）y］≡｛（x，y，z，t）∈Q:p（x，y，z，t）=（ρ-1）y｝，and the following qualitative result can be concluded［10］:any solution system（p，u，Λ）of the evolution filtration problem may be extended to all of Q in pressure and Darcian velocity by

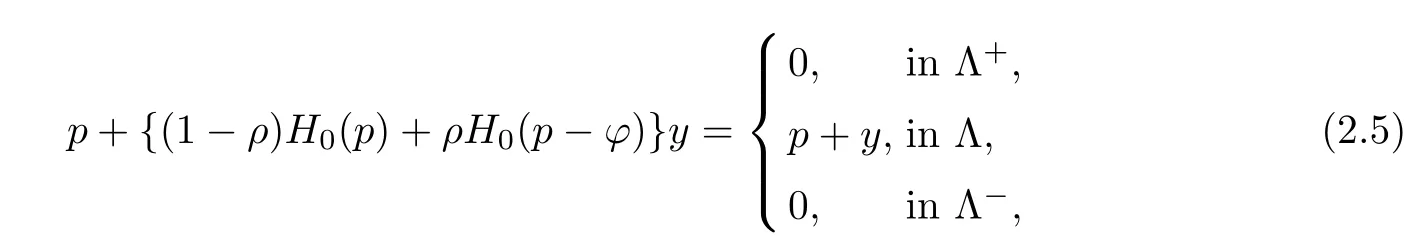
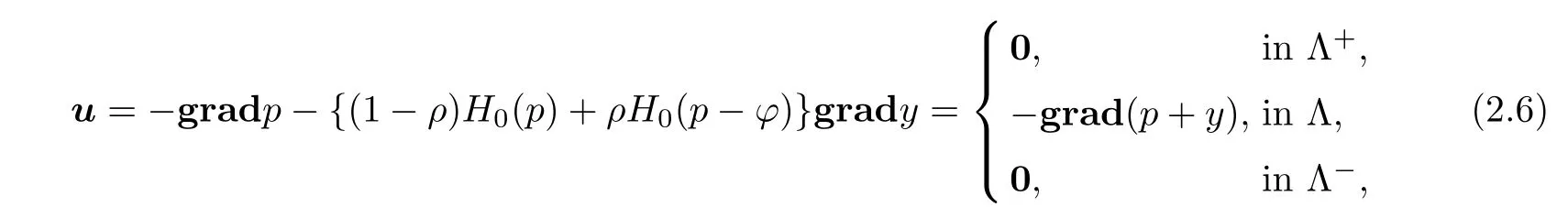
respectively.Here H0denotes the Heaviside function，and ϕ is the continuous Q-extension of the obstacle function in（2.3），by zero in Λ+and by（ρ-1）y in Λ-.

In regard to pressure（hydraulic charge）boundary conditions for this qualitative model，we shall consider

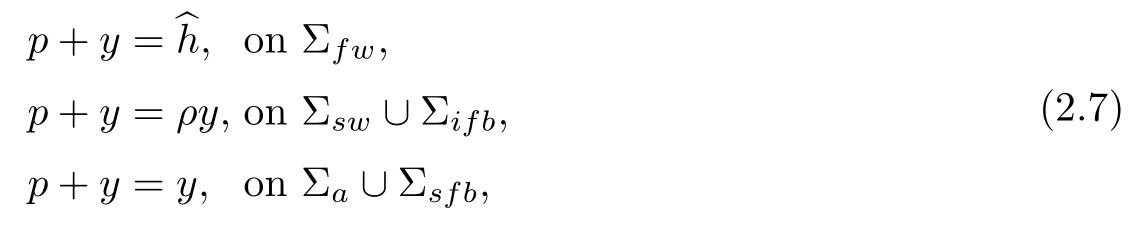
as well as the impervious boundary condition and seepage flux constraint

In addition，as prescribed initial conditions，we have

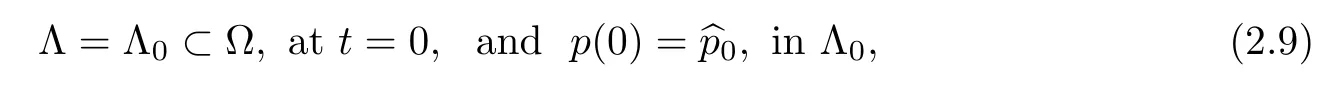
Taking into account qualitative incompressible Darcian flow properties（2.3）-（2.6）and conditions（2.7）-（2.9），the coastal flow problem was formulated in a classical single-phase primal evolution mixed variational form in our previous work［10］，extending the model from the flow domain Λ to the whole domain Q，`a la Baiocchi.Here，our interest is to take a further step:to generate and analyze a general three-dimensional dual evolution mixed variational two-phase flow model，which results indeed to be more suitable for macro-hybridization and parallel variational mixed finite element approximations.

2.2 The Fractional Two-Phase Dual Mixed Physical Model

Neglecting the effect of evaporation，and assigning to the atmospheric pressure a zero value，we shall here consider an immiscible two-phase Darcian incompressible flow，without mass transfer，of a wetting phase denoted by α=w and a nonwetting phase by α=n，in the whole space-time domain Q=Ω×（0，T）.Hence，for a coastal aquifer，non-homogeneous and anisotropic，the governing mixed equations are the following:

here uα，pαand sαare the dependent α-phase variables of velocity，pressure and saturation fields.These are the constitutive and conservation of mass equations of the flow system，where K is the symmetric positive definite absolute permeability tensor，κα，µα，ραand︿qαare the α-phase relative permeability，viscosity，mass density and volumetric flow rate，respectively. Also φ is the porosity of the media and g the gravity acceleration vector.Furthermore，as complementary equations to model（2.10），we have the flow volume balance constraint and the capillary pressure relation

As mentioned in the introduction，our modeling strategy will be to adopt the dual mixed two-phase fractional flow model treated by Chen and Ewing［1］.Thereby，we reformulatephysical two-phase model（2.10）-（2.11）as a fractional flow model，with primary dependent variables the total velocity and global pressure fields

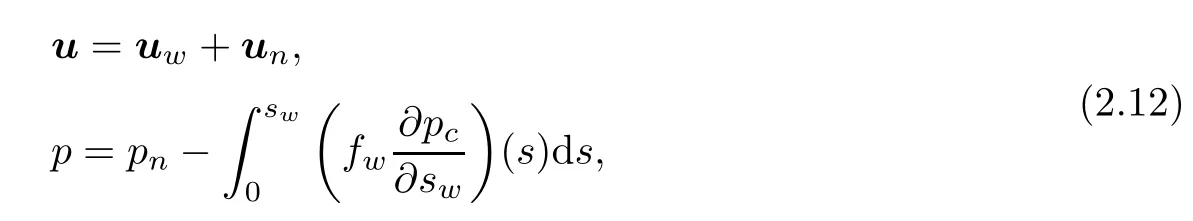
where fα（sw）=λα/λ，α∈｛w，n｝，define the fractional flow functions，in terms of the phase mobilities λα=κα/µαand total mobility λ=λw+λn.Then the dual mixed fractional flow system is given by（see［1］）

and θ is the complementary pressure defined by［18］

Regarding θ as a function of the wetting phase saturation sw，from the inverse relation sw=S（θ）the complementary compressibility would be given by ϑ（θ）=φ∂S（θ）/∂θ.Lastly，we note that the nonwetting phase velocity is related to θ by

Notice that the structure of fractional flow model（2.13）turns out to be of an instantaneous incompressible total velocity-global pressure flow，coupled with an evolution wetting velocitycomplementary pressure compressible-like flow.This mixed structure is proper for dual mixed variational formulations，which，importantly，permit the application of duality principles in their solvability analysis，the development of macro-hybrid spatial decompositions，and preconditioned augmented regularizations.These are the basis in turn for instantaneous penaltyduality algorithms as well as complementary proximation semi-implicit time marching schemes.

The particular natural flow assumption for the open coastal aquifer under consideration，the immobility of the air and seawater phases，will be taken into account，and their modeling consequences will be exhibited，in the next section，where the variational macro-hybridization of the whole system is treated.

2.3 Instantaneous Total Velocity-Global Pressure Variational Model

We next proceed to formulate variationally the instantaneous component of the fractional two-phase flow model（2.13）.Toward this end we apply the duality procedures of［3，19］（also，see［9］）.

Let V（Ω）and Y（Ω）be two given Hilbert spaces for the instantaneous total velocity and global pressure Ω-fields，with trace spaces of boundary normal velocities and pressures denoted by B（∂Ω）and its dual B∗（∂Ω），respectively.Further，let corresponding linear continuous trace operators be denoted by δ∈L（V（Ω），B（∂Ω））and γ∈L（Y（Ω），B∗（∂Ω））.Then as primal and dual operators，we introduce the variational divergence div∈L（V（Ω），Y∗（Ω））and the variational gradient grad∈L（Y（Ω），V∗（Ω）），formally defined by?divv，q?Y（Ω）=RΩdiv v q dΩand?grad q，w? V（Ω）=R

Ωgrad q·w dΩ，for w∈V（Ω），q∈Y（Ω），with V∗（Ω）and Y∗（Ω）denoting the topological duals of V（Ω）and Y（Ω）.

Applying the duality procedure of［3，19］to the pressure-velocity boundary conditions and constraints of the aquifer system，in accordance with those of the qualitative model，（2.7）and（2.8），they are expressed subdifferentially as variational inclusions as follows:

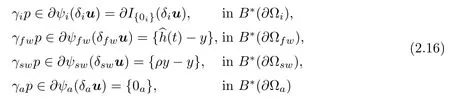
with the seepage flux constraint

here I｛0i｝denotes the indicator functional of the singleton｛0i｝⊂B（∂Ωi），and I｛≥0a｝the indicator functional of the convex subset K≥0a=｛va∈B（∂Ωa）:va≥0ain B（∂Ωa）｝.Then，considering the divergence and normal velocity trace variational operators div∈L（V（Ω），Y∗（Ω））and δ∈L（V（Ω），B（∂Ω）），with transpose divT∈L（Y（Ω），V∗（Ω））and δT∈L（B∗（∂Ω），V∗（Ω）），and utilizing the corresponding variational Green formula

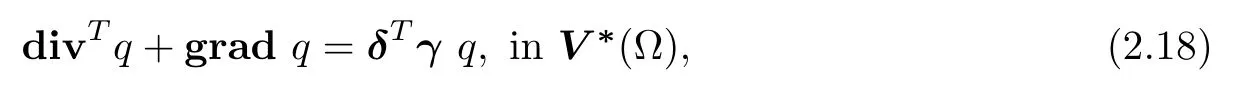
the variational formulation of the incompressible mixed flow component，of the fractional twophase problem is obtained，via the following compositional duality result［19］.

Lemma 2.1 Under the fundamental trace compatibility property［20］

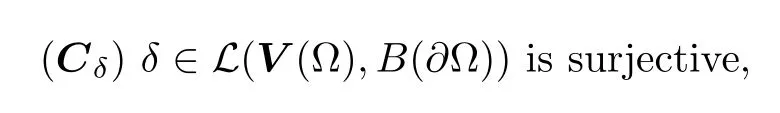
the variational essential boundary condition（2.16）1in B∗（∂Ωi），and the essential boundary constraint（2.17）in B∗（∂Ωa），are such that

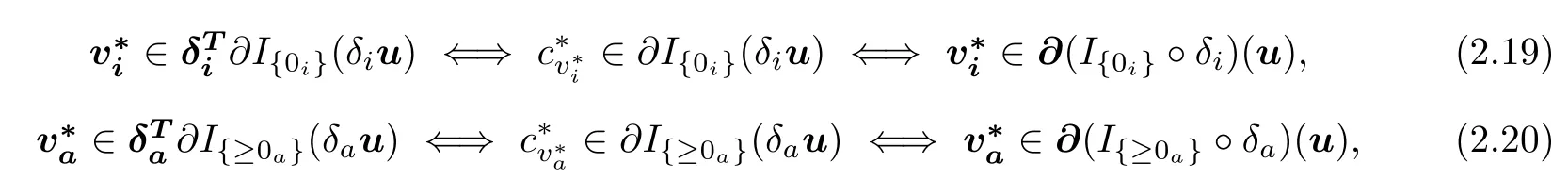
Indeed，the instantaneous dual mixed variational flow component turns out to be

here the primal subdifferentialis such that，for a.e.t∈（0，T），

where∇C（·，t）:V（Ω）→V∗（Ω）is the gradient of the differentiable convex potential C（v，t）= 1/2RΩ（λ（θ（·，t））K）-1v·v dΩ，v∈V（Ω）.Further，

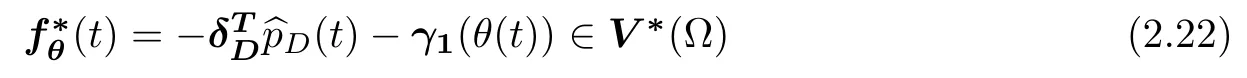
with Dirichlet boundary dataB∗（∂Ωsw）×B∗（∂Ωa），and∂0Ydenotes the zero variational subdifferential in Y（Ω）.For a natural regularity of instantaneous data，we shall assume that

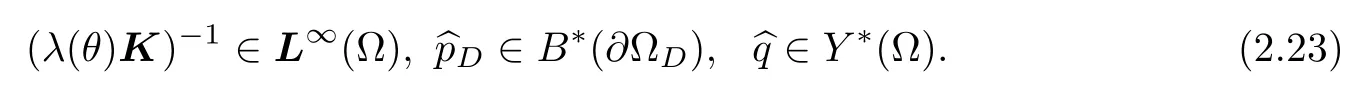
Hence，we adopt the usual velocity-pressure mixed functional Hilbert framework

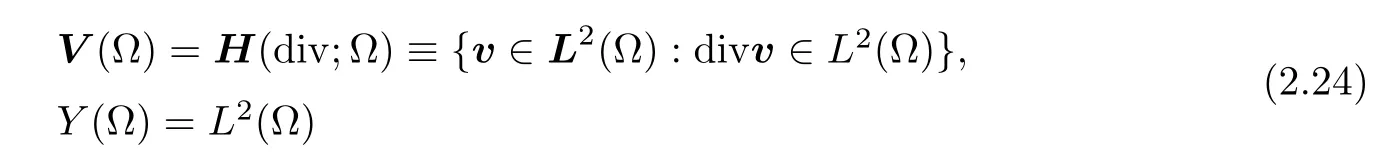
with normal velocity and pressure trace spaces

for which the classical compatibility condition

holds true［20］.We shall denote the kernel of coupling operator div by N（div）⊂V（Ω）. Therefore，applying compositional dualization［3］（see also［21］），we can conclude the following primal composition duality principle.

Theorem 2.2 Mixed problem（M）is uniquely solvable if，and only if，its instantaneous variational primal problem

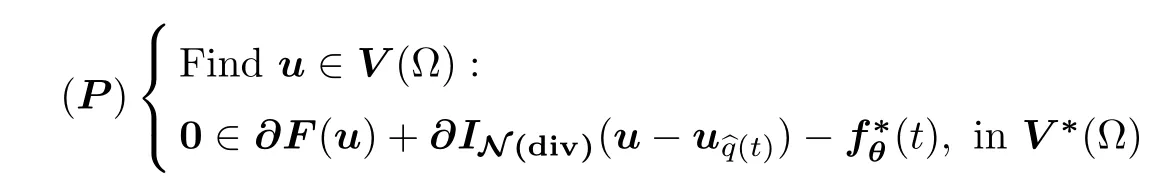
is uniquely solvable，where u︿q（t）is a div-preimage of function︿q（t）.

Thereby，under regularity condition（2.23），in accordance with Theorem 2.2 and the Lax-Milgram Theorem（see［22］，Subsection 2.1），the classical solvability result of problem（M）is achieved.

Theorem 2.3 Instantaneous dual mixed problem（M）possesses a unique solution，continuously dependent on the data.

2.4 Evolution Wetting Velocity-Complementary Pressure Mixed Variational Model

For the variational formulation of the dual evolution mixed component of fractional flow model（2.13），let V（Ω）×Y（Ω）be an appropriate mixed Hilbert functional framework，with pressure dual space such that Y（Ω）⊂Z（Ω）⊂Y∗（Ω），where embeddings are dense and continuous，and pressure pivot space Z（Ω）=L2（Ω）.Then，we consider the following evolution mixed Hilbert spaces

with topological duals V∗=L2（0，T；V∗（Ω））and Y∗=L2（0，T；Y∗（Ω））.Also，for the dual pressure solution space，we consider the corresponding Hilbert space X=｛y:y∈Y，dy/dt∈Y∗｝endowed with the operator norm，continuously embedded in the space C（［0，T］；Z（Ω））of continuous pivot fields.

Once again we apply the duality procedure of［3，19］to compressible-like system（2.13）2，in order to incorporate variationally the pressure-velocity boundary conditions and constraints，of normal wetting velocity and complementary pressure fields.Hence，in accordance with the qualitative physical flow model presented in Subsection 2.1，we consider as before conditions（2.7）and（2.8），in their corresponding subdifferential sense（2.16）and（2.17），with evolution trace spaces B=L2（（0，T）；B（∂Ω））and its dual B∗=L2（（0，T）；B∗（∂Ω））.In this manner，evoking corresponding Green formula（2.18）and Lemma 2.1，the dual mixed variational formulation of evolution subproblem（2.13）2results to be as follows.

where the primal subdifferential∂F:V（Ω）→2V∗（Ω）is given by（2.21），for a.e.t∈（0，T），and the right-hand side term is defined byhere Dirichlet boundary data︿θD（t）= （︿h（t）-y，ρy-y，0a）in B∗（∂ΩD）=B∗（∂Ωfw）× B∗（∂Ωsw）×B∗（∂Ωa）.Also the dual variational operator A∈L（Y∗，Y∗）is formally defined bywith a natural coefficient regularity ϑ（θ）∈L∞（Ω×（0，T））.

Therefore，in the sense of［4］，a dual duality principle can be established for the analysis of evolution mixed variational problem（M），by dualization of its V∗-primal equation and compositional dualization.

Theorem 2.4 Dual evolution mixed problem（M）possesses a unique solution if，andonly if，its dual evolution nonlinear problem

possesses a unique solution，whereis a fixed divT-preimage of function

Thereby，given a specific dual mixed functional Hilbert framework，appropriate variational operator properties and regularity conditions，the well-posedness of problem（M）can be determined.For an existence，uniqueness and regularity analysis of dual evolution problem（D），we refer to Chen's study［2］.

3 Macro-Hybrid Variational Formulations

Once the fractional two-phase dual mixed flow variational problem（M）-（M）has been established，for the open coastal aquifer under consideration，we next specialize the problem in accordance with the qualitative physical stated assumption of air-and seawater-phase immobilities；i.e.，we take into account that the nonwetting-phase velocity field unequals 0 above the sea level（y＞0），and below the sea level（y＜0）.

Toward this end，we reformulate the global problem as a macro-hybrid mixed localized model.This type of variational decomposition is，additionally important，when regarding big spatial scales，heterogeneities and anisotropy of the system，as well as internal variational approximations，finite element implementations and parallel computing.Here we shall follow our study［23］（see，also［4，8］）on macro-hybridization of variational mixed constrained problems in mechanics.

Let us then introduce nonoverlapping domain decompositions of the aquifer spatial region，and derive corresponding dual variational interface continuity transmission problems for synchronization.Hence，let the domain Ω be decomposed in terms of connected disjoint subdomains｛Ωe｝by

assuming Lipschitz internal boundaries and interfaces

In particular，an appropriate specific decomposition of the open aquifer with seawater intrusion，would be the following，with nonoverlapping subdomains above（A）and below（B）the seawater level（y=0）（Fig.1）:

In this manner，we can implement the phase immobilities of the model，obtaining families of air-fresh water and fresh water-seawater flow subsystems，hydraulically communicated acrosstheir interfaces.Thereby，the imposed continuity transmission conditions of the spatial decomposition will correspond，in this case，to the instantaneous normal fresh water velocity and global pressure fields，and to the evolution normal fresh water velocity and complementary pressure fields.

3.1 Instantaneous Macro-Hybrid Mixed Variational Formulations

In this subsection，we treat the macro-hybridization of the instantaneous component of the fractional two-phase flow model，dual mixed problem（M）.

We first note that due to the nonwetting phase immobilities，the total velocity u of the model corresponds to the wetting fresh water velocity field，uw，above and below the sea level.Hence，for the macro-hybridization of problem（M），we consider nonoverlapping domain decompositions of type（3.1）-（3.3），and mixed functional framework（2.24）-（2.25）of wetting fresh water velocity and global pressure fields assumed to be decomposable in the sense

with corresponding global pressure pivot space

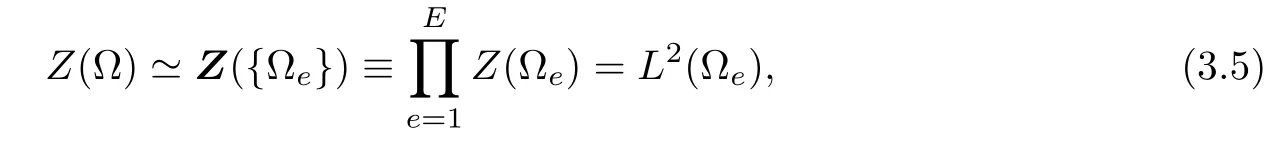
Hence，imposing the primal transmission condition of（3.4）1，via the subdifferential of the indicator functional IQof transmission subspace Q，the macro-hybridized version of mixed problem（M）is achieved，

Furthermore，incorporating the internal boundary global pressures as Lagrange multipliers， denoted by，the macro-hybrid variational formulation of mixed problem（M）is obtained once the following dualization result is applied［5］.

Lemma 3.1 Due to compatibility property（C［δΓe］），the corresponding macro-hybrid compositional dualizationholds true.

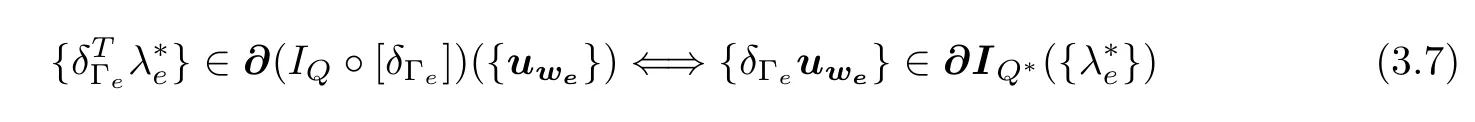
Indeed，we have the macro-hybrid problem

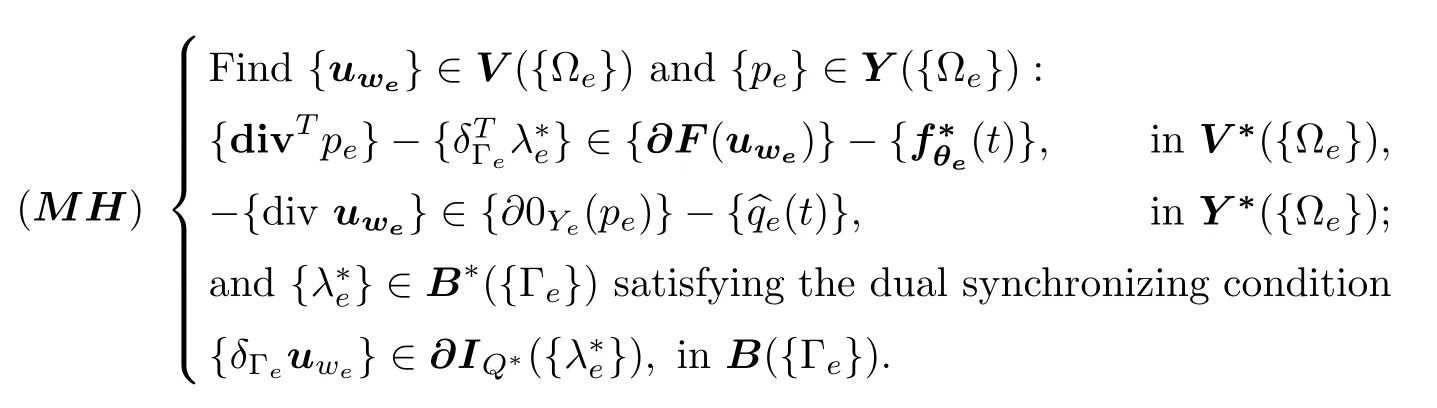
This is the localized instantaneous dual mixed incompressible flow model（M），above and below the sea level，related to the nonoverlapping specific spatial decomposition（3.3）of the open coastal aquifer.Its dependent mixed fields are the local wetting fresh water velocities and the global pressures（with nonwetting pressure，the zero atmospheric pressure；see（2.12）2），synchronized by the internal boundary global pressures.Notice that，under seawater，the seepage constraint term primal subdifferential｛∂F｝must be zero，∂（I｛≥0a｝◦δa）=0（see（2.21））.

3.2 Evolution Dual Macro-Hybrid Mixed Variational Formulations

Next，proceeding similarly as before，the macro-hybridization of the complementary dual evolution mixed model（M）turns out to be

where the evolution mixed functional framework V｛Ωe｝and Y｛Ωe｝，of wetting fresh water velocity and complementary pressure fields，corresponds to the decomposed version of evolution mixed spaces（2.26），relative to decomposed mixed framework（3.4）-（3.5）and on the basis of specific decomposition（3.3）.Furthermore，introducing the Lagrange multiplier｛χ∗e｝∈∂IQ（｛δΓeue｝）⊂B∗｛Γe｝of internal boundary complementary pressures，the macro-hybrid variational formulation of evolution mixed problem（M）is finally obtained by applying macro-hybrid compositional dualization result（3.7）of Lemma 3.1.

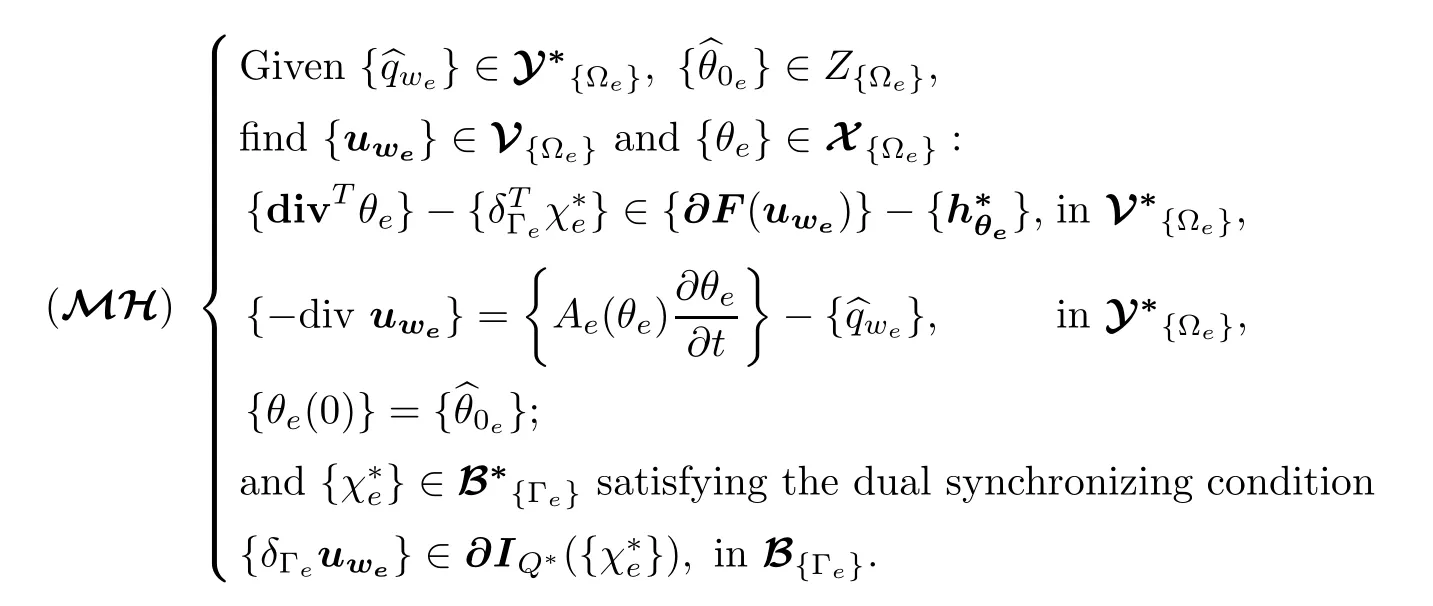
As noted in the previous subsection for the instantaneous component of the fractional two-phase flow model，under seawater the seepage constraint term of the primal subdifferential｛∂F｝must be zero（see（2.21））.

4 Parallel Proximation Algorithms

In this final section，we state proximation algorithms for the fractional two-phase flow macro-hybrid mixed variational models of the theory.These algorithms have proved to be very efficient in the treatment of mixed variational inclusions［3，4］.We should further emphasize that all of these schemes are indeed implementable in terms of local internal variational finite element approximations，as we comment below，which in general may correspond to non-matching spatial discretizations.

For the instantaneous macro-hybrid dual mixed incompressible model（MH），preconditioned augmented variational formulations are constructed in the sense of two-and three-field variational versions［3］.On the other hand，for the complementary coupled dual evolution macro-hybrid mixed compressible-like model（MH），corresponding proximal-point algorithms are semi-implicit time marching schemes of the Douglas-Rachford and Peaceman-Rachford type，with proximation characterizations［4］.

Remark 4.1 For semi-discrete spatial approximations of the instantaneous macro-hybrid dual mixed variational component，（MH），of the coastal filtration flow model，we observe that a natural approach is the introduction of finite dimensional internal variational frameworks［24］，implementable in terms of finite element interpolating basis.That is，the distributed local fresh water velocity and global pressure mixed framework may be approximated in terms of given families of finite dimensional subspacesand，such that

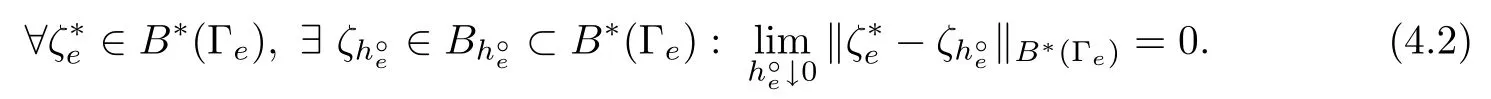
We refer to［4］（Sect.4）for further details，as well as for related semi-discrete solvability composition duality principles.For numerical implementation and experimentation，we refer to the works［25，26］，where proximation iterative algorithms，as the ones to be presented in this section，are applied and discussed.Importantly，we should notice that corresponding macrohybrid mixed finite element implementations，in general，turn out to be globally nonconforming，allowing their generation via non-matching geometrical meshes，a fundamental strategy in parallel computing.Of course，similar comments on finite element approximations for the dual evolution component of the coastal filtration flow model，（MH），are in order，concerning the macro-hybrid mixed frameworks of the distributed local fresh water velocity and complementary pressure fields，as well as internal boundary complementary pressure fields.

4.1 Parallel Proximal-Point Algorithms

Following the resolvent or proximation methodology treated in［3，4，8］，for the construction of preconditioned augmented two-and three-field parallel proximal-point algorithms of variational inclusions，we shall consider instantaneous macro-hybrid dual mixed model（MH）expressed in the classical mixed subdifferential form

Hence，we shall have the primal and dual field identifications

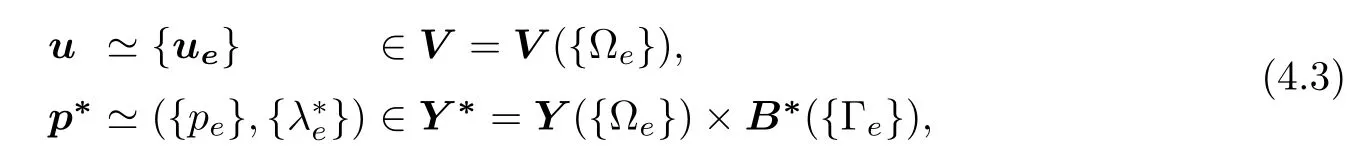
and the operator relations

here A:V → 2V∗is a primal maximal monotone operator with domain D（A）≃｛｛ve｝∈V（｛Ωe｝）:｛δieve｝= ｛0ie｝｝，Λ ∈L（V，Y）is a linear continuous coupling operator with transpose ΛT∈L（Y∗，V∗），and∂G∗:Y∗→2Yis a dual maximal monotone subdifferential operator with effective domain D（G∗）≃｛（｛qe｝，｛µ∗e｝）∈Y（｛Ωe｝）×B∗（｛Γe｝）:｛µ∗e｝∈Q∗｝.

Next，we shall proceed to state parallel proximal-point algorithms for the abstract general mixed variational problem（S），making precise in the sequel the sense in which the algorithmic results apply to the macro-hybrid dual mixed incompressible flow model of the theory，（MH）.

4.1.1 Two-Field Instantaneous Algorithms

Following［3］，problem（S）is first reformulated as a two-field augmented proximation problem，in terms of a real fixed parameter r＞0，and a given linear and symmetric preconditioningoperator M∗:Y∗→Y，m∗-bounded below，with inverse denoted by M-∗:Y→Y∗.

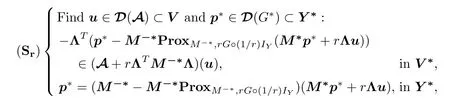
In the construction of proximation augmented version（Sr），we should observe that the dual equation of mixed problem（S）is equivalently expressed in its augmented preconditioned form M∗p∗+rΛu∈（M∗+r∂G∗）（p∗），which upon the introduction of the M∗-resolvent operator of the dual subdifferential∂G∗:Y∗→2Y，defined by（a single valued 1/m∗-firm contraction），takes the final formThen problem（Sr）is completed utilizing the resolvent-proximation relationProxM∗，rG∗=IY∗-M-∗ProxM-∗，rG◦（1/r）IY◦M∗（see［3］）.

Thereby，mixed augmented problem（Sr）that in fact corresponds to an exact r-penalization of original problem（S）（see［25］for a concrete case），turns out to be well conditioned.Then it becomes natural to associate Uzawa type algorithms for its resolution［27-29］，as the following one.

Algorithm IGiven u0∈D（A），p∗0∈D（G∗），known um，p∗m，m≥0，find um+1，and p∗m+1:

In the convergence analysis of Algorithm I，taking into account the above stated resolventproximation relation，a resolvent dual characterization of the algorithm is given by

that corresponds to a characterization of the implicit mixed Euler scheme

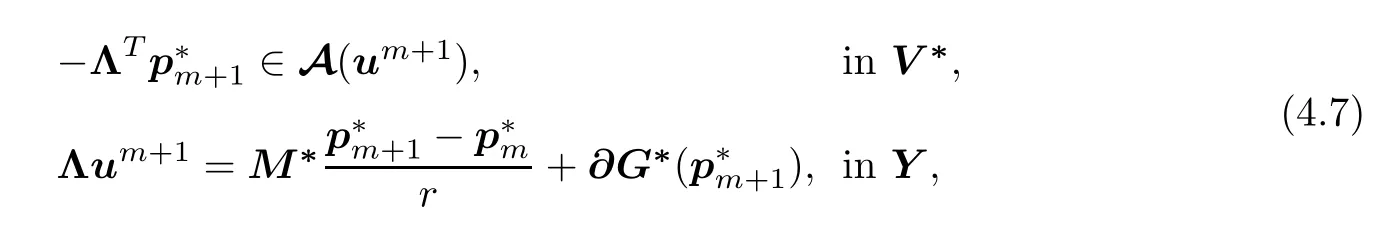
related to the dynamical system associated to augmented problem（Sr）.Here the dual operator A∗Λ:Y∗→ 2Yis defined by A∗Λ=-ΛA-1（-ΛT（·）），with A-1:V∗→2Vthe inverse（graph）of primal operator A:V→2V∗.Then the convergence of the algorithm is concluded［30］.

Theorem 4.2 The convergence of Algorithm I is guaranteed whenever the dual operator conditionis fulfilled.

·Model（MH） In the case of the macro-hybrid dual mixed incompressible flow model of the paper，the parallel implementation of this two-field proximal-point algorithm，with vector and operator relations（4.3）and（4.4）in force，follows by observing that corresponding primal superpotential G of dual subdifferential（4.4）4is given byand that corresponding proximation operator（4.5）turns out to behere Proj［H-∗e］，Qstands for the［H-∗e］-projection on Q，with the inverse preconditioning operator identification

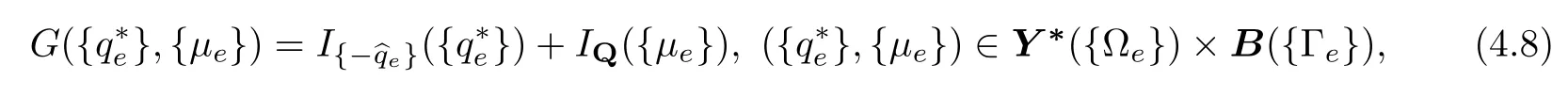
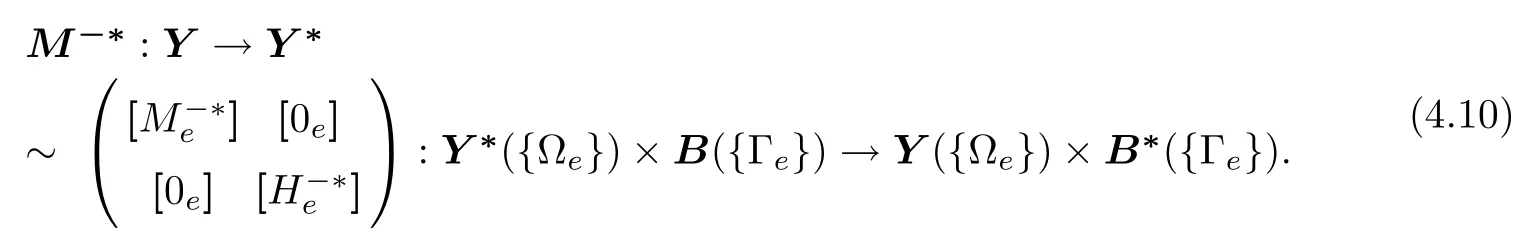
In this manner，for the wetting fresh water velocity-global pressure flow component of the two-phase coastal filtration model，Algorithm I takes the explicit local and parallel form

Algorithm IMHGivenknown

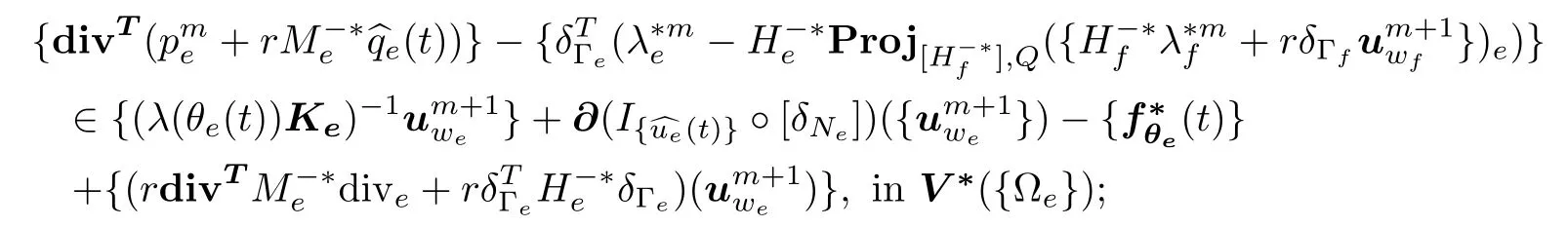
Moreover，in this case，convergence conditionof Theorem 4.2 is satisfied.

4.1.2 Three-Field Instantaneous Algorithms

A second proximal-point algorithm for mixed problem （S）corresponds to a three-field extended formulation，for which the intermediate primal field

is introduced，and the dual equation is inverted or dualized，to obtain the three-field variational abstract problem

Then，proceeding as for the original two-field mixed problem（S），a further augmented formulation turns out to be the following，

Notice that at this instance the proximation operator of the formulation vanishes，in contrast with that of augmented problem（Sr）.

Therefore，for augmented three-field mixed problem（Sr），an alternative Uzawa type proximalpoint algorithm reads as follows.

Algorithm II Given p∗0∈D（G∗），known p∗m，m≥0，find um+1，τm+1and p∗m+1:

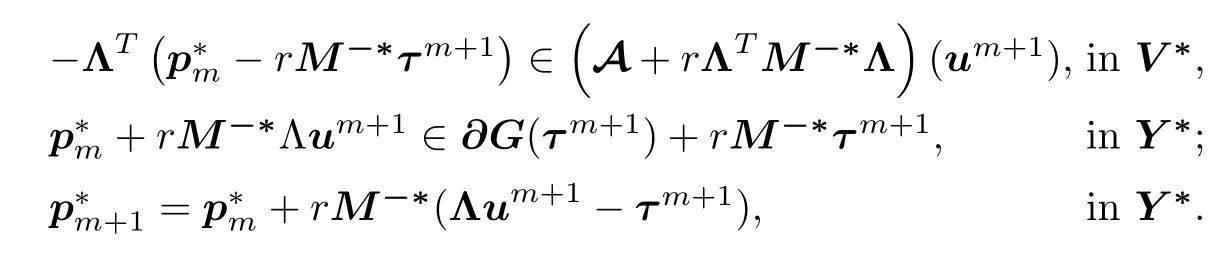
Once again，this algorithm can be interpreted as an implicit Euler scheme，

with a resolvent dual characterization，

Then，due to the 1/m∗-firm contraction property of the resolvent operator，the convergence of the algorithm is given as follows［30］.

Theorem 4.3 Algorithm II converges，if its dual operator is such that

It is important to recognize that Algorithm II constitutes an extension of the classical penalty-duality algorithm ALG1 studied in［29-32］，with further alternating-direction variants ALG2 and ALG3.

·Model（MH） For the macro-hybrid dual mixed incompressible flow model component of the paper，with relations（4.3）and（4.4）in force，intermediate field τ=Λu ∈Y，（4.11），is given by

the negative divergence of local wetting fresh water velocities and the internal boundary normal wetting fresh water velocities；a subgradient of dual subdifferential（4.4）4.Then Algorithm II for instantaneous macro-hybrid dual mixed model（MH），in terms of preconditioning operator（4.10），takes the local and parallel implementable form

Algorithm IIMHGivenknownm≥0，find

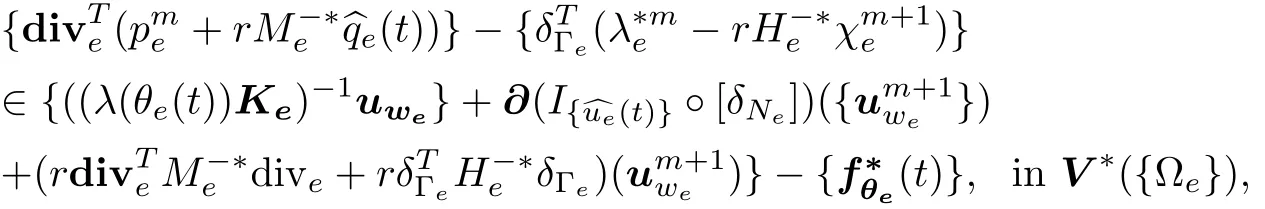
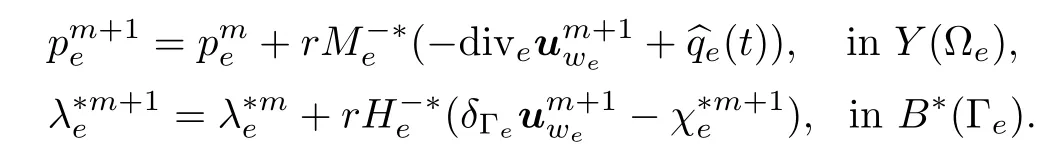
Moreover，condition（CA∗Λ，∂G）of Theorem 4.3 is satisfied and Algorithm IIMHis convergent.

4.2 Proximation Semi-Implicit Time Marching Schemes

Next，we proceed to apply time discretization schemes to the dual evolution macro-hybrid mixed variational component of the coastal fractional flow model，（MH）.We shall consider semi-implicit time marching schemes that are implementable as proximation local parallel algorithms.In particular，we apply the Douglas-Rachford and Peaceman-Rechford time marching procedures.Also，based on our previous work［8］on proximal-point algorithms for variational constrained problems，corresponding stationary convergence results are stated.

4.2.1 The Operator Splitting Douglas-Rachford Scheme

For dual evolution macro-hybrid mixed variational problem（MH），with identifications（4.3）and（4.4）in force，and denoting by r＞0 and m≥0 the time marching step and step number，the Douglas-Rachford time marching procedure is given as follows（see［4，8］）.

For a proximal realization of this scheme，we introduce the intermediate macro-hybrid vector｛κe｝∈B｛Γe｝，such that

Then the Douglas-Rachford procedure has as a parallel proximal realization the following.

Algorithm IMHGiven，knownsatisfying the primal synchronizing condition

4.2.2 The Operator Splitting Peaceman-Rachford Scheme

As an alternative operator splitting scheme for dual evolution macro-hybrid mixed variational problem（MH），we consider the following.

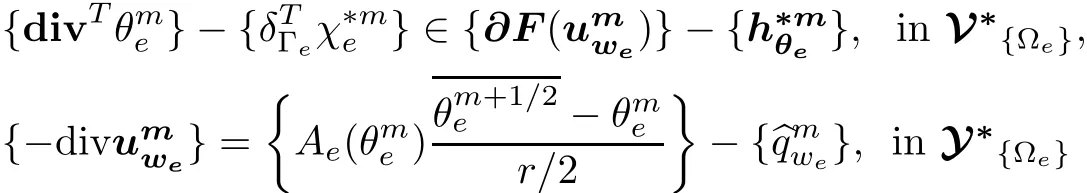
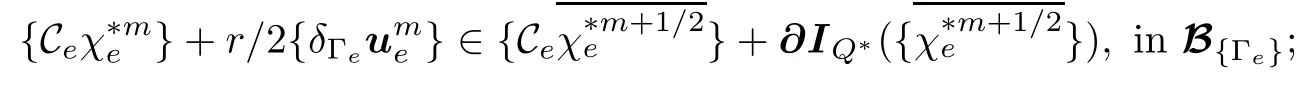
Similarly，as for the previous time marching scheme，we introduce an intermediate macrohybrid vector｛κe｝∈B｛Γe｝，but now such thatand a parallel proximation realization of Peaceman-Rachford scheme is then concluded.

Algorithm IIMHGivenknown，findsatisfying the primal synchronizing condition

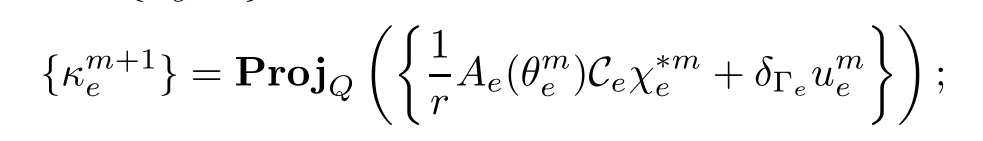
4.3 Convergence of the Operator Splitting Schemes

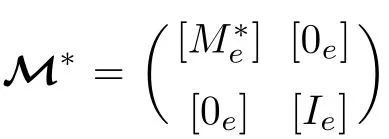
Thereby，defining the auxiliary dual supervectorsuch thatthe macro-hybrid dual problem of the Douglas-Rachford scheme，at the m+1≥1 time step，can be expressed by

On the other hand，for the Peaceman-Rachford scheme，its macro-hybrid dual problem can be similarly expressed as follows，where the dual subdifferential is given by∂G∗=（｛0∗e｝，∂IQ∗）.Therefore，we can conclude the following convergence results［4］.

Theorem 4.4 Let the dual operatorsbe maximal monotone.Then， for time-independent dataoperator splitting algorithms

Algorithm IMHand Algorithm IIMHevolve，as m → ∞，to aand astationary state of the dual evolution macro-hybrid mixed filtration coastal problem（MH），respectively.

［1］Chen Z，Ewing R.Mathematical analysis of reservoir models.SIAM J Math Anal，1999，30:431-453

［2］Chen Z.Degenerate two-phase incompressible flow I，existence，uniqueness and regularity of a weak solution. J Differ Equ，2001，171:203-232

［3］Alduncin G.Composition duality methods for mixed variational inclusions.Appl Math Opt，2005，52: 311-348

［4］Alduncin G.Composition duality methods for evolution mixed variational inclusions.Nonlinear Analysis: Hybrid Syst，2007，1:336-363

［5］Alduncin G.Macro-hybrid variational formulations of constrained boundary value problems.Numerical Funct Anal Opt，2007，28:751-774

［6］Alduncin G.Analysis of evolution macro-hybrid mixed variational problems.Int J Math Anal，2008，2: 663-708

［7］Alduncin G.Primal and dual evolution macro-hybrid mixed variational inclusions.Int J Math Anal，2011，5:1631-1664

［8］Alduncin G.Parallel proximal-point algorithms for constrained problems in mechanics//Yang L T，Paprzycki M.Practical Applications of Parallel Computing.New York:Nova Science，2003:69-88

［9］Alduncin G.Analysis of augmented three-field macro-hybrid mixed finite element schemes.Analysis in Theory and Applications，2009，25:254-282

［10］Alduncin G.Evolution filtration problems with seawater intrusion:Macro-hybrid primal mixed variational analysis.Front Eng Mech Research，2013，2:22-27

［11］Esquivel-Avila J，Alduncin G.Qualitativeanalysisofevolution filtration freeboundary problems//Proceedings of the Second World Congress on Computational Mechanics.Stuttgart:University of Stuttgart，1990:658-661

［12］Baiocchi C，Comincioli V，Magenes E，et al.Free boundary problems in the theory of fluid flow through porous media:existence and uniqueness theorems.Ann Mat Pura Appl，1973，4:1-82

［13］Torelli A.Su un proplema a frontiera libera di evoluzione.Bolletino U M I，1975，11（4）:559-570

［14］Torelli A.On a free boundary value problem connected with a non steady phenomenon.Ann Sc Norm Super Pisa Cl Sci，1977，IV:33-58

［15］Friedman A，Torelli A.A free boundary problem connected with non-steady filtration in porous media. Num Anal，TMA，1977，1:503-545

［16］Gilardi G.A new approach to evolution free boundary problem.Commun Partial Differ Equ，1979，4: 1099-1122

［17］DiBenedetto E，Friedman A.Periodic behaviour for the evolutionary dam and related free boundary problems.Commun Partial Differ Equ，1986，11:1297-1377

［18］Arbogast T.The existence of weak solutions to single porosity and simple dual-porosity models of two-phase incompressible flow.Nonlinear Analysis，1992，19:1009-1031

［19］Alduncin G.Variational formulations of nonlinear constrained boundary value problems.Nonlinear Analysis，2010，72:2639-2644

［20］Girault V，Raviart P A.Finite Element Methods for Navier-Stokes Equations.Berlin:Springer-Verlag，1986

［21］Alduncin G.Composition duality principles for mixed variational inequalities.Math Comput Model，2005，41:639-654

［22］Alduncin G.Mixed variational modeling of multiphase flow and transport in the subsurface.Far East J Appl Math，2012，71:1-42

［23］Alduncin G.Numerical resolvent methods for macro-hybrid mixed variational inequalities.Num Funct Anal Opt，1998，19:667-696

［24］Temam R.Analyse Num´erique.Paris:Presses Universitaires de France，1970

［25］Alduncin G，Vera-Guzm´an N.Parallel proximal-point algorithms for mixed finite element models of flow in the subsurface.Commun Numer Methods Eng，2004，20:83-104

［26］Alduncin G，Esquivel-´Avila J，Vera-Guzm´an N.Steady filtration problems with seawater intrusion:macro-Hybrid penalized finite element approximations.Int J Num Methods in Fluids，2005，49:935-957

［27］Brezzi F，Fortin M.Mixed and Hybrid Finite Element Methods.New York:Springer-Verlag，1991

［28］Roberts J E，Thomas J-M.Mixed and hybrid methods//Ciarlet P G，Lions J L.Handbook of Numerical Analysis，Vol II.Amsterdam:North-Holland，1991:523-639

［29］Fortin M，Glowinski R（eds）.M´ethodes de Lagrangien Augment´e:Applications`a la R´esolution Num´erique de Probl`emes aux Limites.Paris:Dunod-Bordas，1982

［30］Gabay D.Application de la m´ethode des multiplicateurs aux in´equations variationnelles//Fortin M，Glowinski R.M´ethodes de Lagrangien Augment´e.Paris:Dunod-Bordas，1982:279-307

［31］Glowinski R.Numerical Methods for Nonlinear Variational Problems.New York:Springer-Verlag，1984

［32］Glowinski R，Le Tallec P.Augmented Lagrangian and Operator-Splitting Methods in Nonlinear Mechanics. Philadelphia:SIAM，1989

［33］Mosco U.Dual variational inequalities.J Math Anal Appl，1972，40:202-206

E-mail：alduncin@geofisica.unam.mx