思维介入操作活动 体验数据的随机性

浙江湖师附小教育集团（313000） 朱国平

思维介入操作活动 体验数据的随机性

浙江湖师附小教育集团（313000） 朱国平

在小学阶段，学生对于抽象的、理论的可能性概念理解起来有一定的困难，只能借助试验的数据来加以体会。因此，通过对教学的分析，把“统计与概率”作为一个整体来教学，最理想的方式是在数据统计的过程中渗透概率的思想，在概率的学习过程中应用统计的方法。

概率统计 不确定事件 可能性 随机性

概率统计是研究随机性（不确定事件）的数量关系。所谓不确定事件，是指在相同的条件下，重复同样的试验或观测，所得的结果不确定，以至于在试验之前无法预料试验的结果。《数学课程标准》（2011版）对概率教学的调整是比较大的，既删减了教学内容，又降低了教学要求，主要教学目标指向随机现象中的可能性。而现行人教版小学数学教材在五年级上册安排了如下内容：例1，体验事件发生的确定性和不确定性；例2，列出所有可能发生的结果，感受可能性是有大小的；例3，根据数据推测事件发生的可能性的大小。

那么，如何在操作活动中使学生体验事件发生的可能性是有大小的，同时试验操作的过程和结果又是随机的呢？我们以例2教学为例，进行了以下的尝试。

教学过程：

1.对事件发生前结果的预测——操作前的思维介入

操作材料：布袋中放入3颗黑色围棋子，2颗白色围棋子。

操作要求：从布袋中任意摸出一颗围棋子，记录它的颜色后，放回去摇匀继续摸；两人轮流摸，一共摸10次。

操作记录表：

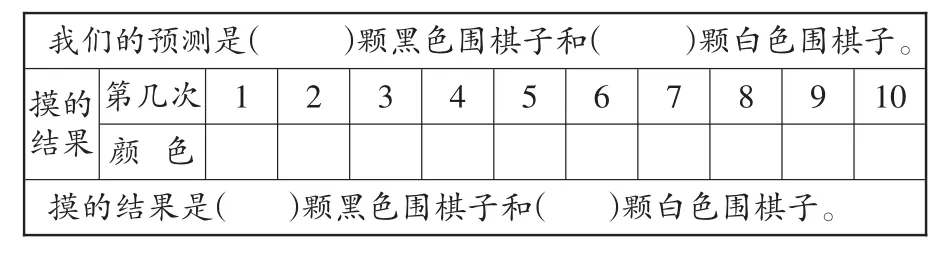
我们的预测是（ ）颗黑色围棋子和（ ）颗白色围棋子。摸的结果第几次1 2 3 4 5 6 7 8 9 10颜色摸的结果是（ ）颗黑色围棋子和（ ）颗白色围棋子。

操作前设问：

（1）如果在口袋里摸围棋子，你们觉得摸到什么颜色的围棋子可能性大一些？（师板书：数量多，可能性大；数量少，可能性小）

（2）如果摸10次，请你们先预测，摸到几次白色围棋子和几次黑色围棋子？

（3）你们的预测有根据吗？

2.对事件发生过程时的预测——操作中的思维介入

（1）演示操作。（形式：两个学生摸围棋子，师记录）

操作时设问：

①请你们预测一下，首先会摸到什么颜色的围棋子？

②（一生连续摸到2颗白色围棋子）请你预测一下，下一次摸到什么颜色的围棋子？（生：白色）

③你们的预测有根据吗？你们不是认为黑色的围棋子多吗？为什么反而选白色的围棋子呢？（学生认为前两次摸到的都是白色的围棋子）

④前面两次摸的结果会影响第三次吗？（不会，也可能摸到黑色的围棋子）

⑤（学生继续操作，连续摸到3颗黑色的围棋子后）请你们预测一下，下一次摸到什么颜色的围棋子？（摸到黑白颜色的围棋子都有可能）

学生完成后，记录、统计成表。

（2）实践操作（形式：同桌操作，相互记录）。（略）

3.对事件发生后的评价——操作后的思维介入

（1）明确事件发生的可能性大小，体验数据的随机性。

师随机将10组学生模的结果反馈在黑板上，如下表。

黑色围棋子 7 5 8 6 9 5 6 7 4 8白色围棋子 3 5 2 4 1 5 4 3 6 2

整理后设问：

①摸围棋子之前，我们大部分同学都预测摸到“黑色围棋子多，白色围棋子少”，我们观察黑板上的结果，哪些是符合的？

②这里有7组结果与“黑色围棋子多，白色围棋子少”这个预测是一样的，还有哪些组的结果也是这样？看到这样的结果，你有什么想说的？

生1：我觉得摸的结果可能和我们的预测会不一样。

生2：什么情况都有可能发生。

师：看来，袋子里黑色围棋子多，所以摸到的结果大部分是黑色围棋子，符合我们之前的预测——数量多，可能性大。

③那怎么解释“5，5”“4，6”这样的结果呢？

生3：摸到的结果可能和预想的不一样。

生4：我认为摸到的球是随便的，摸到10个白色围棋子也说不定。

师：老师更正你一个词语，你说的“随便”可以改为“随机”。

④有学生提出，把10次结果合起来。（结果为摸到黑色围棋子65次，摸到白色围棋子35次）

师：对合起来的结果，你有什么想说的？（黑色围棋子多，白色围棋子少，符合预测的结果）

（2）深入体验数据的随机性。

师（投影出示下表）：我们来看看这两组（5，5）的结果。

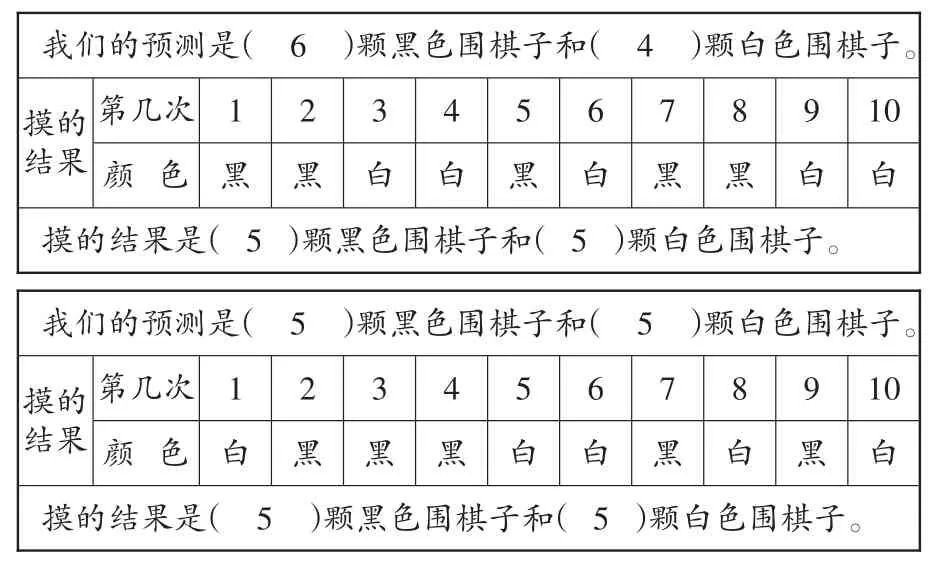
我们的预测是（ 6 ）颗黑色围棋子和（ 4 ）颗白色围棋子。摸的结果第几次1 2 3 4 5 6 7 8 9 10颜色黑黑白白黑白黑黑白白摸的结果是（5）颗黑色围棋子和（5）颗白色围棋子。我们的预测是（ 5 ）颗黑色围棋子和（ 5 ）颗白色围棋子。摸的结果第几次1 2 3 4 5 6 7 8 9 10颜色白黑黑黑白白黑白黑白摸的结果是（ 5 ）颗黑色围棋子和（5）颗白色围棋子。

整理后设问：

①这两组都是5黑5白，请仔细观察他们的记录，你有什么想说的？

生5：一组预测对了，一组预测错了。

生6：我发现虽然都是5黑5白，但摸到黑色围棋子和白色围棋子的顺序是不一样的。

②还有没有小组摸到的结果也是5黑5白的？（有3组）你们摸到黑色围棋子和白色围棋子的顺序与他们一样吗？（都不一样）

③同样是5黑5白，但摸到的顺序是不一样的，看到这样的结果，你又有什么想说的？（摸的结果是一样的，摸的顺序是随机的）

④哪些小组的预测和摸的结果是一样的？如果让你们再摸一次，还会是这个结果吗？

生7：可能还是这个结果。

生8：可能结果会不一样。

生9：可能摸的结果还是一样的，但摸到的顺序不一样。

⑤通过刚才摸围棋子的活动，你有什么想说的？

生10：摸围棋子的结果是随机的，摸之前只是预测，不能确定。

师：刚才这位同学的总结给了我们启发，我们可以做这样一件事，即把全班同学摸围棋子的结果加起来，看看摸到的围棋子中什么颜色多。小组长先计算，再交给课代表汇总。

……

教学思考：

1.操作的目的不是为了解释、证明理论概率

许多随机现象可以从理论上进行分析，对相应的事件指定一个合理的概率，即理论概率。但在小学阶段，学生对于抽象的、理论的可能性概念理解起来有一定的困难，只能借助试验的数据来加以体会。本课教学中，袋里有“3黑2白”围棋子，摸到黑色围棋子的可能性是60%，摸到白色围棋子的可能性是40%，我们会给学生概括出“数量多，可能性大；数量少，可能性小”的结论，这个结论无疑是准确的。但值得注意的是，试验操作的目标不是证明这个事实是正确的，而是在操作中使学生体会可能性的大小，其实这就是用数据统计的方法去直观感受理论概率。把“统计与概率”作为一个整体来教学，最理想的方式是在数据统计的过程中渗透概率的思想，在概率的学习过程中应用统计的方法。

2.操作的目的是应用数据体验事件发生的随机性

五年级教材有关可能性的教学内容是对事件发生的定性思考，只要求学生体会随机现象，并能对随机现象发生的可能性大小做定性描述，这部分内容是具有可操作性的。通过操作前和操作时的预测及操作后的评价，引领学生的思维介入操作活动，体会事件的发生是随机的，可预测但无法确定；通过对试验数据的结构分析（分类整理），印证可能性既是有大小的，又是随机的；通过对试验过程的再现（5黑5白的顺序），再次印证事件发生的随机性；最后通过增加试验的次数，即把小组、全班所有数据都整合起来，再次体会事件发生的可能性是有大小的，因为随着试验次数的增加，事件发生的可能性逐渐逼近事件发生的概率。

（责编 蓝 天）

G623.5

A

1007-9068（2015）05-035