MorPhological Undecimated Wavelet DecomPosition Fusion Algorithm and Its APPlication on Fault Feature Extraction of Hydraulic PumP
2015-11-21SunJian孙健LiHongru李洪儒WangWeiguo王卫国YePeng叶鹏
Sun Jian(孙健),Li Hongru(李洪儒),Wang Weiguo(王卫国),Ye Peng(叶鹏)
Mechanical Engineering College,Shijiazhuang 050003,P.R.China
MorPhological Undecimated Wavelet DecomPosition Fusion Algorithm and Its APPlication on Fault Feature Extraction of Hydraulic PumP
Sun Jian(孙健),Li Hongru(李洪儒)*,Wang Weiguo(王卫国),Ye Peng(叶鹏)
Mechanical Engineering College,Shijiazhuang 050003,P.R.China
Since vibration signals of hydraulic pump are mostly nonlinear and traditional fusion algorithm cannot satisfyingly process them,a morphological undecimated wavelet decomposition fusion(MUWDE)algorithm is proposed.Eirstly,under the framework of morphological undecimated wavelet decomposition(MUWD),multichannel signals are decomposed.Approximate signals of all decomposition layers are selected by feature energy factor and fused according to the presented fusion rules.Eurthermore,specific method for optimal selection of MUWDE parameters is presented to avoid subjective influences.Einally,the proposed algorithm is verified by simulation signals and pump vibration signals.
morphological undecimated wavelet decomposition(MUWD);information fusion;feature extraction;hydraulic pump
0 Introduction
Mechanical diagnosis and prognostics require effective information detected by multi-sensors to extract precise fault feature.Vibration signals of hydraulic pump caused by early fault are mostly nonlinear[1]due to structural characters.And the feature information ingredient is relatively weak. As a result,appropriate fusion algorithm is required for extracting precise fault feature effectively.
Currently,various fusion algorithms have been proposed for mechanical feature extraction[2-3].However,weighted fusion algorithm is subjected to fusion weights[4-5].Kalman filtering algorithm lacks strict filtering functions for nonlinear system[6-7].The wavelet analysis fusion algorithm may neglect the feature information during the sampling operation[8-9].Consequently,fusion performance based on conventional algorithm is not satisfying and the fault feature is hard to effectively extract,which fails to meet the requirements of precise diagnosis and prognostics.
As an efficient nonlinear signal processing method,morphological undecimated wavelet decomposition(MUWD)omits the sampling operation during decomposition and reconstruction,which effectively avoids distortion[10-11].MUWD has been widely used for mechanical signal processing[12-13].However,in conventional MUWD,the approximate signal in the highest decomposition layer is considered as result.Others are neglected,thus feature information is missed.Each sensor typically sends one bit of information about fault feature rather than send the observed requirements[14].Therefore,an appropriate fusion rule is required to modify conventional MUWD.
Therefore,Based on the framework of conventional MUWD,the novel morphological undecimated wavelet decomposition fusion(MUWDE)algorithm is proposed.Multi-channel signals are respectively decomposed firstly.Approximate signals in decomposition layers are selected according to feature energy factor(EEE).Based on the presented fusion rules,the feature information is generally used and the signals are reconstructed.Eurthermore,we use the fusion energy entropy(EEE)to measure fusion performance of MUWDE with various combinations of parameters,and demonstrate the optimization method in detail.Simulation and experimental results show the validity and superiority of the proposed algorithm.
1 MUWDF Algorithm
1.1 Introduction of MUWDF
Assume that collections of V and W are the i th signal space and i th detail space,respectively,and T(·)denotes the morphological operator. Eramework of conventional MUWD can be describe by Eqs.(1—3)[15]

where Eq.(1)is to use signal analysis operator φ↑ito decompose signal from Vito Vi+1;Eq.(2)is to use detail analysis operatorω↑ito decompose signal from Vito Vi+1;Eq.(3)denotes that the composition operatorand the analysis operators meet wavelet reconstruction and pyramid principle,which avoid information missing during signal analysis and composition[16-17].
Through the framework analysis,we can identify T(·)as the key calculation of MUWD[18].Normal ones are mean combination operator,morphological difference operator,morphological gradient operator and hybrid operator[19-20].Considering pump structural characters,the morphological difference operator is selected.It contains both black and white Top-Hat,which can effectively extract signal pulses[21].Therefore,basic calculation of MUWDE can be described as
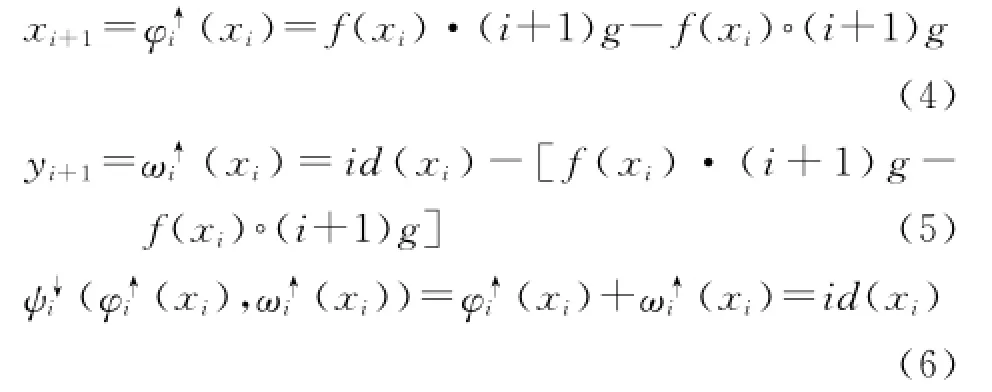
where f(n)is the initial signal and g(n)the structure element;"and"·denote operations of morphological open and morphological close;(i+1)g means the i th swelling operation on flat element.Based on operator,fault feature information is extracted from the former layer and restored in current approximate signal,which is to be the initial signal for decomposition next.
1.2 Fusion of multi-channel signals based on MUWDF
Consider that X1—X3respectively refer to the signal in Channel1—Channel3 probed by Sensor1—Sensor3.Suppose that the number of decomposition layers is N.
Signals are decomposed by Eqs.(4—6). Then approximate signals in all N decomposition layers of X1are obtained as,…,N};for X2,the approximate signals arej=1,…,N};and for X3,they are x3=.To measure various contributions for feature information ofandEEE is defined.EEE can be described as the ratio between partial energy of the prior h doubling frequency of feature frequency and the total energy in frequency domain.Its expression is described as
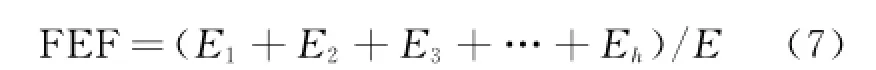
where Ehdenotes the energy of the h th feature frequency.In this article,we set h=3.Obviously,EEE can better reflect the feature information proportion.The higher the EEEis,the larger the proportion is.Therefore,for the i th layer,we can respectively calculateofofandofby Eq.(7).Consequently,fusion rule for signals in thesame decomposition layer is demonstrated as follows.
Fusion Rule 1 Eor the j th decomposition signalsthe one with the maximum EEE will be selected.
Based on fusion rule 1,parts of approximate signals of X1remain and parts of X2and X3are absorbed as well.Therefore,feature redundant information and complementary information are utilized initially.We can select approximate signals in all decomposition layers of X1—X3according to fusion rule 1.Define the collection of selected approximate signals C={y1,y2,…,yN},and the collection W={w1,w2,…,wN}of EEE values.Means for calculating fusion weights kiis described as

Consequently,selected approximate signals can be fused by

Therefore,the second fusion rule is:
Fusion Rule 2 Eor the selected approximate signals in collection C,calculate the corresponding fusion weights and reconstruct the signal according to Eq.(9).
Based on fusion rule 1,fusion rule 2 realizes abundant use of feature information and reconstructs the signal by fusion of approximate signals for achieving the global decision.
2 OPtimization of Parameters
According to the theory of MUWDE,two parameters are involved.One is N,the number of decomposition layers;the other is L,the initial length of flat structure element.
If N is too large,information in detail signal will be extremely few,so that the ingredient in approximate signal almost stays invariant.
If N is too small,information in detail signal will be too much,so that the extracted feature will be unclear.
If L is too large,extracted pulses will decrease,leading to the loss of feature information.
If L is too small,noises may be retained in the reconstruction signal.
Therefore,specific method for optimal selection of parameters of N and L will be detailed.
Eirstly,ranges of N and L are supposed to be confirmed.Suppose that lengths of signal X1—X3are Len1—Len3.After searching the whole sequence of X1,the local maximum collection is LY1={LY1ii=1,…,NLY1}and the minimum collection is LV1={LV1ii=1,…,NLV1},where NLY1and NLV1are the number of local maximum dots and minimum dots,respectively.Similarly,for X2and X3,we can get collections LY2,LV2,LY3and LV3.Correspondingly,collections of distances of local maximum are DY1={d Y1i= LY1i+1-LY1ii=1,…,NLY1-1},DY2and DY3. Collections of distances of local minimum are DV1={d V1i=LV1i+1-LV1ii=1,…,NLV1-1},DV2and DV3.Then the range of N can be calculated by Eqs.(10—12).


where fsdenotes the sampling frequency and f0the feature frequency.Calculation for the number of combination of N and L is
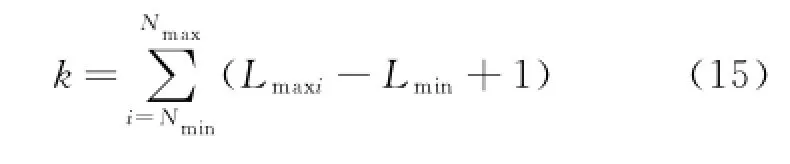
In order to search for the optimal combination,we present EEE to evaluate fusion performance.Eor each combination(suppose N=n,L= l),consider that Eidenotes the energy of approximate signal yiselected by fusion rule 1.Then EEE is defined as
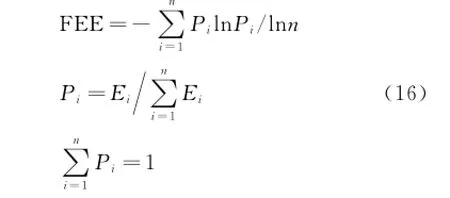
According to Eq.(16),we can know that EEE can describe signal complexity and fusion performance.The lower the EEE is,the simpler the signal ingredient will be and the more obvious the feature information will be.Consequently,by comparing values of EEE of each combination,we can select the one with the minimum EEE to be the optimum.
Above all,the fusion process of multi-channel vibration signals of hydraulic pump is described in Eig.1.
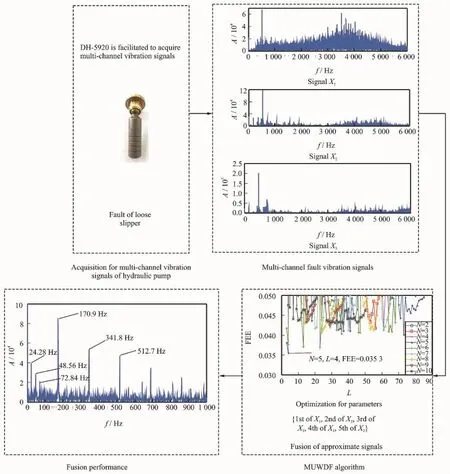
Eig.1 Eusion process of multi-channel hydraulic pump vibration signals
3 Simulation Analysis
In order to verify the fusion performance of MUWDE,simulation signals are analized.Consider that fs=1 024 Hz,and sampling time t=1 s.Simulation signals are y1(t),y2(t)and y3(t)

It is clear that the signals mainly consist of three parts,fault signal x1(t),harmonic wave signal x2(t)and white noise n(t).x1(t)means the simulation of pulse signal with periodic index decrease because of rolling bearing fault.The striking frequency is f0=16 Hz,the striking function in every period is e-200tsin(2π×256t)and the resonance frequency is 256 Hz.x2(t)represents the harmonic wave signal cos(2π×40t)+ cos(2π×50t),which contains the frequencies of 40 Hz and 50 Hz.And the difference frequency is 10 Hz.y1,y2and y3are various combinations of x1(t),x2(t)and n(t),which imitate the multichannel vibration signals probed by various sensors.Eigures of time domain and frequency domain of the simulation signals are shown in Eig.2 and Eig.3,respectively.
In Eig.3,we can see that modulation in the resonance frequency 256 Hz exists in all signals. And fault feature frequency 16 Hz emerges by noises.Therefore,the proposed MUWDE algorithm is used to fuse y1,y2and y3for effective feature information extraction.
(1)Optimization for MUWDE parameters N and L
Based on the analysis of local maximums and minimums of the simulation signals,we can calculate Nmin=2 and Nmax=8 by Eqs.(10—12). Eor each N=2,3,…,8,there is a corresponding region for L.As fs=1 024 Hz and f0=16 Hz,various ranges of L can be achieved by Eqs.(13— 14),and listed in Table 1.
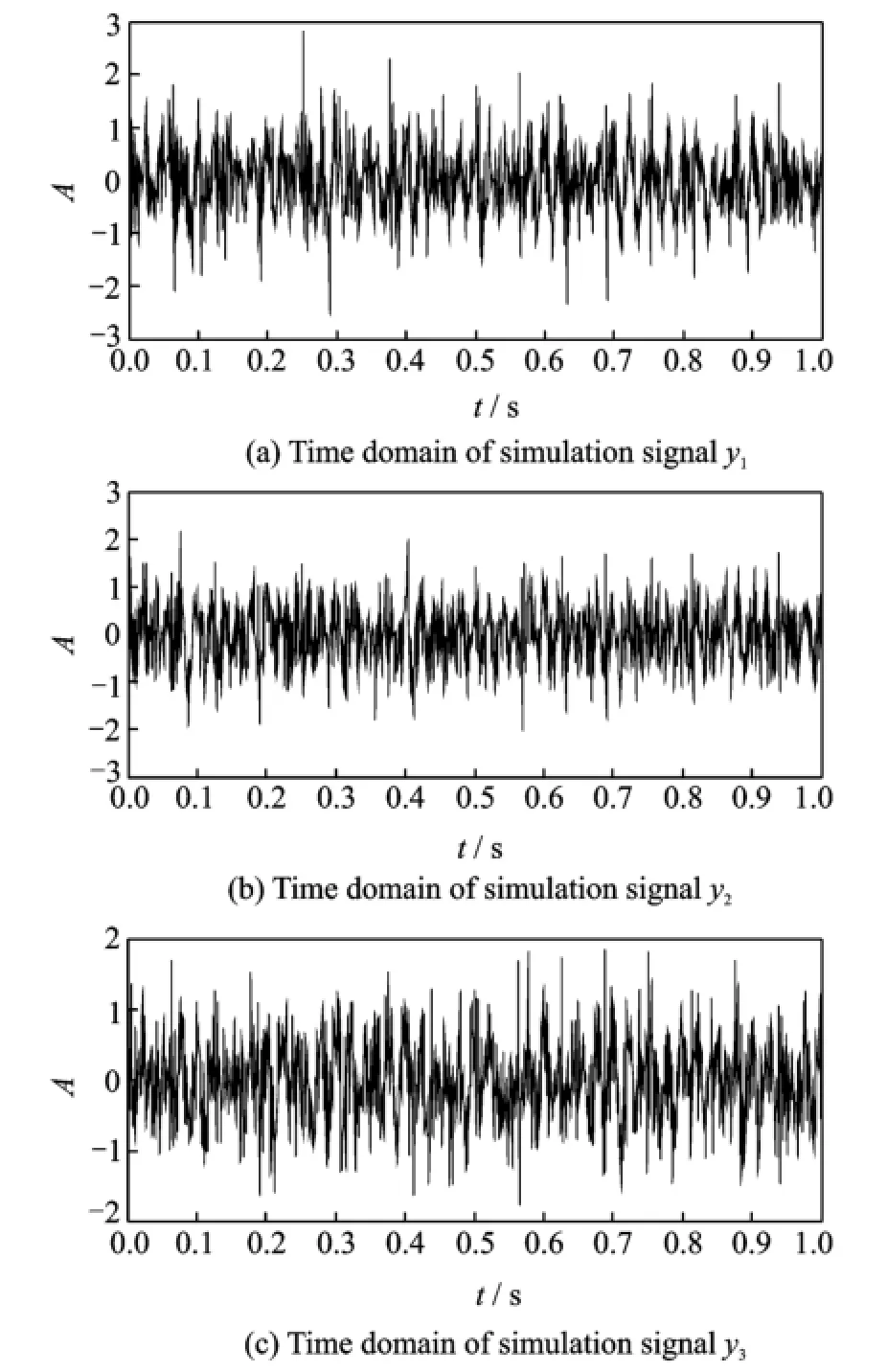
Eig.2 Time domain of multi-channel simulation signals

Table 1 Various combinations of Parameters N and L
According to Eq.(15),there are 97 combinations of N and L.Each combination has its own EEE calculated by Eq.(16),which is shown in Eig.4.And Eig.5 is the amplification of Eig.5 in area 0—0.05.
Eig.4 shows 97 values of EEE with various parameter combinations.Each curve refers to the changing of EEE along with L for every settled N.It is clear that each curve exists a minimum. On this base,we can find the minimum EEE for each N,which is{0.182 9,0.038 4,0.0132,0.008 9,0.004 2,0.007 7,0.008 1}.Eig.5 clearly shows the values of EEE ranging from 0 to 0.05.Conclusions can be drawn that the best fusion performance is achieved by MUWDE with combination of N=6 and L=7.The minimumEEE is 0.004 2.

Eig.3 Erequency domain of multi-channel simulation signals

Eig.4 EEE change with various combinations of N and L
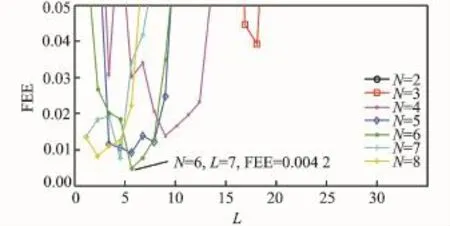
Eig.5 Amplification of EEE ranging from 0 to 0.05
(2)Analysis of MUWDE fusion performance
Eirstly,simulation signals y1,y2and y3are decomposed according to Eqs.(4—6).g0=[0 0 0 0 0 0 0]and N=6.According to Eq.(7),EEE of each decomposition layer of y1is{0.252 0,0.042 1,0.246 2,0.073 2,0.031 8,0.007 7}. Similarly,EEE of y2is{0.217 1,0.137 4,0.170 3,0.095 7,0.005 3,0.068 4}and EEE of y3is{0.303 2,0.109 8,0.061 8,0.084 1,0.009 4,0.028 1}.Then they are selected based on fusion rule 1.We take the first decomposition layer for example,and envelops of the corresponding approximate signals are shown in Eig.6.
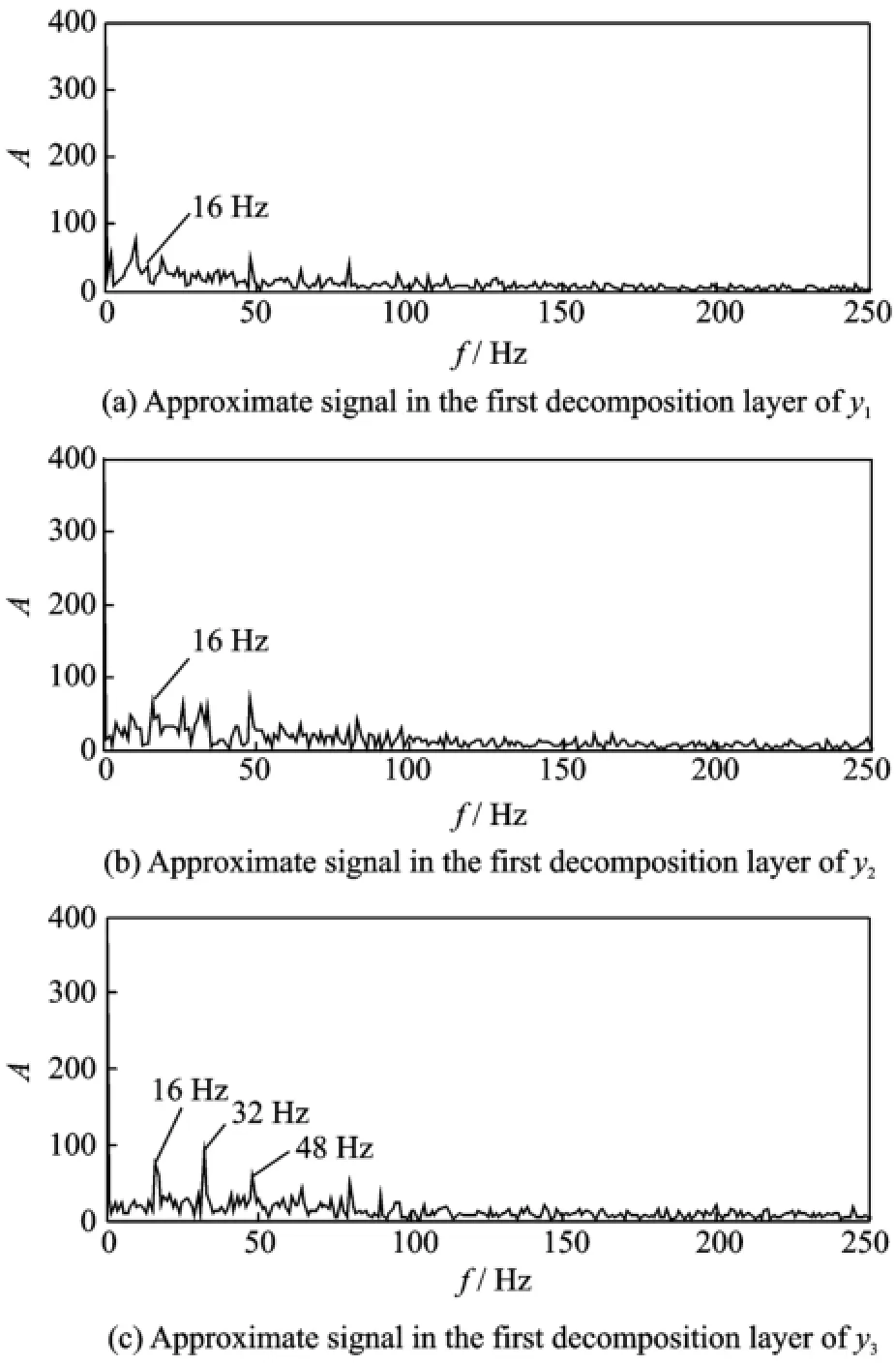
Eig.6 Approximate signals in the first decomposition layer of multi-channel signals
Eig.6 shows the envelops of approximate signals in the first decomposition layer.In Eig.6(a,b),the feature frequency 16 Hz still emerges by noises.However,in Eig.6(c),16 Hz and its double frequency are relatively obvious.The phe-nomenon corresponds with EEE of these approximate signals y1—y3,which are 0.252 0,0.217 1 and 0.303 2.According to fusion rule 1,as 0.303 2>0.252 0>0.217 1,the approximate signal of y3in the first decomposition layer is remained.Similarly,remained approximate signals in other layers are 2nd of y2,3rd of y1,4th of y2,5th of y1and 6th of y2.The corresponding values of EEE are{0.303 2,0.137 4,0.246 2,0.095 7,0.031 8,0.068 4}.
Eusion weights are achieved by Eq.(8),which are k1=0.343,k2=0.156,k3=0.280,k4= 0.108,k5=0.036,k6=0.077.Signal is reconstructed by fusing 6 approximate signals using Eq.(9):

where yij(i=1,2,3 and j=1,2,…,6)denotes the approximate signal in the jthdecomposition layer of yi;yfinalthe reconstructed signal.Eusion result is shown in Eig.7.

Eig.7 Eusion performance of multi-channel simulation signals based on MUWDE(N=6,L=7)
Eig.7 shows that by the general use of feature information in multi-channel signals,the feature frequency 16 Hz and its doubling frequency are obvious.Eurthermore,the direct frequencies 40 Hz and 50 Hz are restrained and the modulation in 256 Hz is settled.To better indicate the advantages of MUWDE,we take conventional methods,such as weighted averaging fusion algorithm,Kalman filtering algorithm and wavelet analysis algorithm,to fuse the same multi-channel signals for comparison.Results are shown in Eig.8.
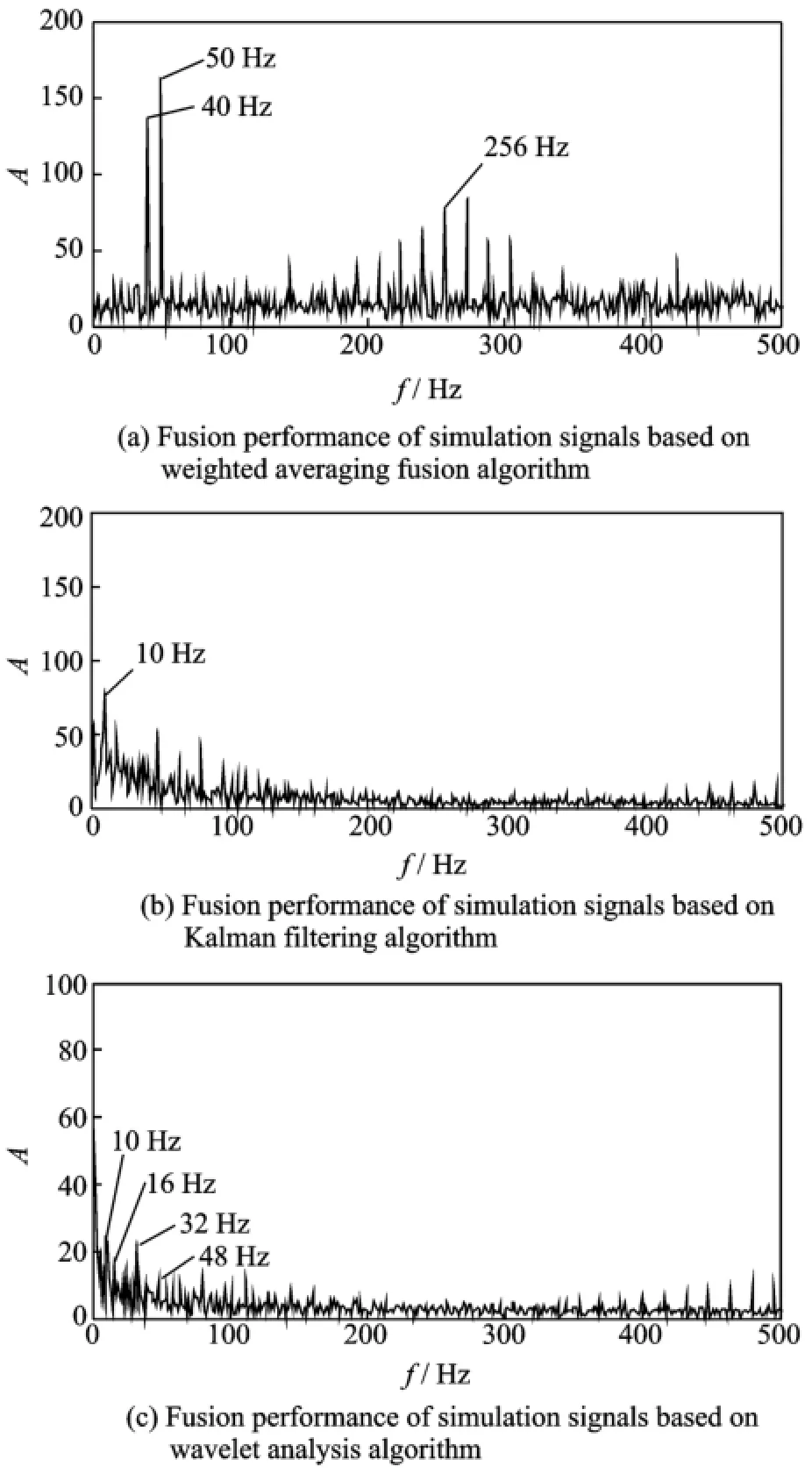
Eig.8 Comparison of fusion performance of multichannel signals based on conventional fusion algorithms
Eig.8(a)shows the fusion performance of multi-channel signals based on weighted averaging algorithm.It is clear that there are still harmonic waves and modulation ingredient,and the feature information is not effectively extracted. Eig.8(b)describes the fusion performance based on Kalman filtering algorithm.As the inherent disadvantages of the method,the fusion result is not satisfying.Although the harmonic waves and modulation are restrained,the feature information is still not clear and the difference frequency 10 Hz exists.Eig.8(c)indicates the fusion performance based upon wavelet analysis algorithm. The feature frequency and its doubling frequency are basically extracted.However,some feature information is neglected because of threshold se-lection and re-sampling process.Eurthermore,the difference frequency 10 Hz still exists in the fused signal.Consequently.It is concluded that compared with conventional algorithms,the proposed MUWDE algorithm has advantages in both disturbance restraining and feature information extracting.
4 ExPerimental Results
In order to verify the effectiveness and utility of the proposed algorithm,MUWDE is applied in the fusion of loose slipper(Eig.9)multi-channel vibration signals of hydraulic pump.The tested hydraulic pump is SY-10MCY14-1EL with 7 pistons.The driving dynamo is Y132M-4,with the settled speed of 1 480 r/min and the period of 0.041 s.Installation of the vibration sensors is shown in Eig.10.Sampling frequency is 12 000 Hz.The sampled vibration signals are saved in computer by DH-5920 dynamic signal testing and analyzing system.

Eig.9 Eault of loose slipper

Eig.10 Installation of vibration sensors on hydraulic pump
Signals observed by Sensor1—Sensor3 are respectively saved as X1—X3.Eig.11 shows the time domain.And frequency domain is shown in Eig.11.
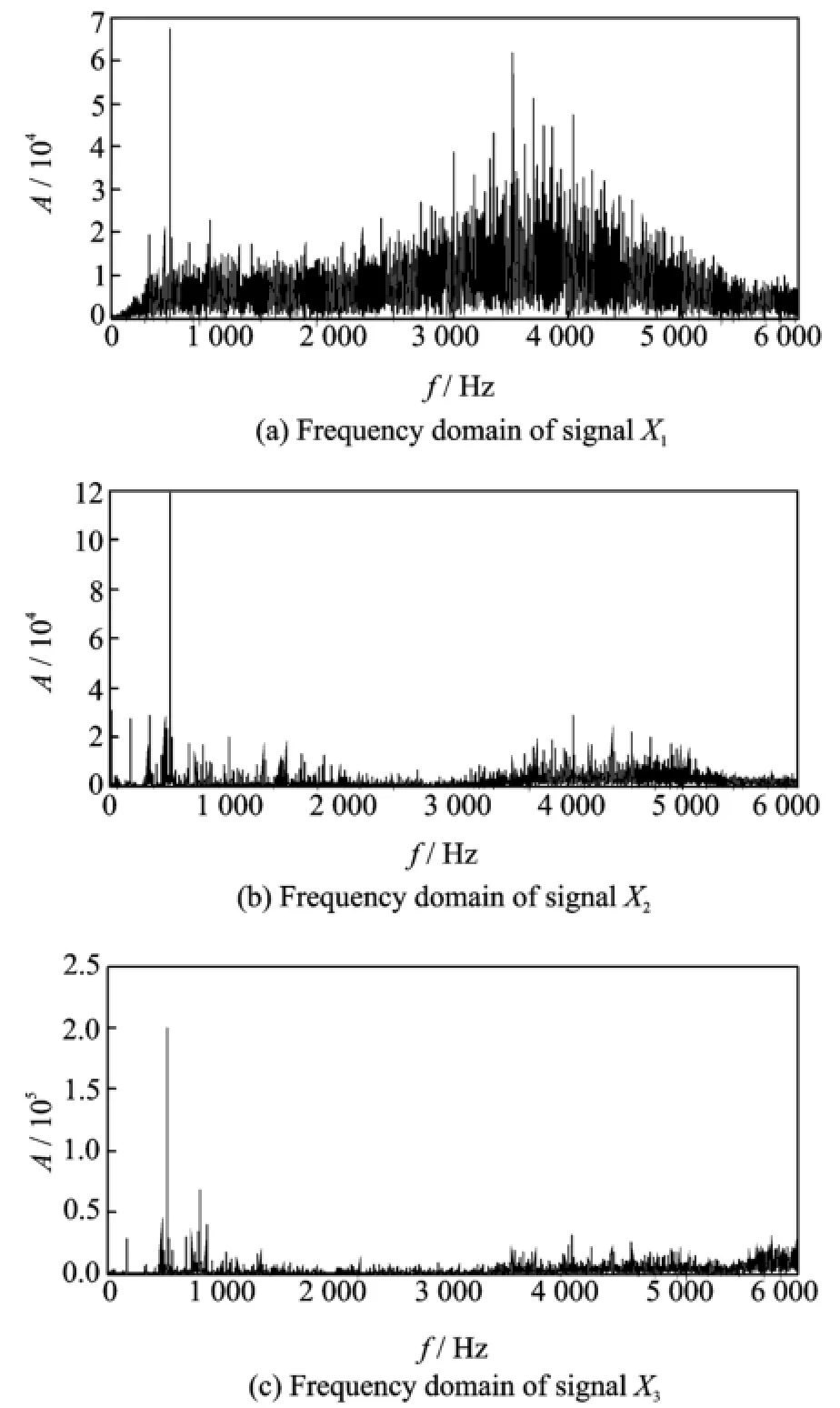
Eig.11 Erequency domain of multi-channel signals of hydraulic pump
In Eig.11,it is clear that all the three signals have modulation phenomena and the amplitude in 517 Hz is relatively strong.Since the real speed of pump is 1 480 r/min,the rotating bearing frequency is 1 480/60=24.6 Hz.As there are 7 pistons,the inherent striking frequency is 24.6× 7=172.2 Hz.Therefore,this frequency is supposed to exist in each vibration signal.Eor single loose slipper fault,its feature frequency should be equal or approximate to the rotating bearing frequency 24.6 Hz.However,both the inherent frequency and the fault feature frequency submerge by noises.Therefore,the multi-channel signals will be fused by MUWDE.
According to Eqs.(10—12),we can get that Nmin=2 and Nmax=10.Eor each N=2,3,…,10,there will be a corresponding region for L.As fs=12 000 Hz and f0=24.6 Hz,the variousranges of L can be achieved by Eqs.(13—14),which are listed in Table 2.

Table 2 Various combinations of N and L
According to Eq.(15),there are 949 combinations of N and L.And each combination has its own EEE which is calculated by Eq.(16).Consequently,there are 9 curves consist of 949 groups of EEE.Collection of the minimum EEE of each curve is{0.052 0,0.041 6,0.041 4,0.035 3,0.037 2,0.040 9,0.041 3,0.042 3,0.042 9}. Eig.12 is the amplification of EEE ranging from 0.03 to 0.05.

Eig.12 Amplification of the curves in the region of EEE ranging from 0.03 to 0.05
In Eig.12,it is clear that the global minimum EEE(EEE=0.035 3)is achieved when N=5 and L=4.Therefore,with the selected parameters,the multi-channel vibration signals are fused by the proposed MUWDE.g0=[0 0 0 0]and N=5.Signals X1,X2and X3are decomposed by multi-scaled difference operator according to Eqs.(4—6).According to Eq.(7),EEE of each decomposition layer of X1is{0.028 7,0.022 6,0.030 9,0.035 6,0.026 8}.Similarly,EEE of X2is{0.028 1,0.047 7,0.054 4,0.031 8,0.031 5}and EEE of X3is{0.027 3,0.038 9,0.061 2,0.032 1,0.030 4}.Based on fusion rule 1,the selected approximate signals are{1st of X1,2nd of X2,3rd of X3,4th of X1,5th of X2}.Values of EEE are{0.028 7,0.047 7,0.061 2,0.035 6,0.031 5}.Then fusion weights are achieved by Eq.(8),which are k1=0.140,k2=0.233,k3=0.299,k4=0.174,k5=0.154. Consequently,the signal is reconstructed based on the fusion of 5 approximate signals by Eq.(9)
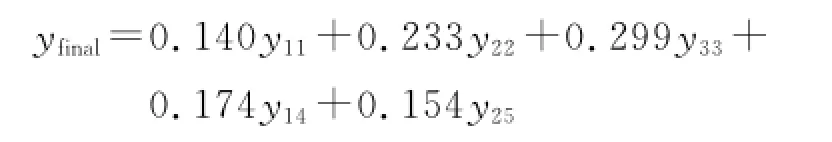
where yij(i=1,2,3 and j=1,2,…,5)denotes the approximate signal in the jthdecomposition layer of yi;and yfinalthe reconstructed signal.Eusion result is shown in Eig.13.

Eig.13 Experimental fusion results of multi-channel vibration signals based on MUWDE when N=5 and L=4
In Eig.13,feature frequency 24.28 Hz(24.28 Hz≈24.46 Hz)and its doubling frequency are effectively extracted,as well as the inherent vibration frequency 170.9 Hz(170.9 Hz≈172.2 Hz).Noises and modulation phenomenon are better processed.To further indicate the advantages of MUWDE,we take the multi-scaled wavelet fusion(MWE)algorithm in Ref.[9]for comparison.Eusion result is shown in Eig.14.

Eig.14 Experimental results of multi-channel vibration signals processed by MWE algorithm
By comparison between Eig.14 and Eig.13,we can see that MWE is only able to extract in-herent frequency information.However,parts of feature information are neglected due to threshold selection and re-sampling.Therefore,feature information is not effectively utilized.Eurthermore,we can respectively calculate values of EEE and EEE after MWE fusion.Results are EEE= 0.051 5 and EEE=0.049 8.It is obvious that EEE of MUWDE is lower than that of MWE(0.035 3<0.051 5).And EEE of MUWDE is higher than that of MWE(0.069 4>0.049 8). Conclusions can be drawn that compared with MWE,feature information are effectively utilized by MUWDE so that the extracted feature information is more obvious.
5 Conclusions
An effective fusion algorithm for vibration signals of hydraulic pump based on MUWDE is proposed in this article.On one hand,approximate signals in various decomposition layers are selected by feature energy factor and fused for reconstruction.On the other hand,method for parameters optimal selection of MUWDE is demonstrated in detail.Simulation and experimental results show that compared with conventional algorithms,MUWDE can achieve better fusion performance and effectively extract feature information of hydraulic pump.It will help condition based maintenance.
Acknowledgement
This work was supported by the National Natural Science Eoundation of China(No.51275524).
[1] Wang H W,Wu H Q.Reliability evaluation model based on data fusion for aircraft engines[J].Transactions of Nanjing University of Aeronautics&Astronautics,2012,29(4):318-324.
[2] Ciuonzo D,Papa G,Romano G,et al.One-bit decentralized detection with a rao test for multi-sensor fusion[J].IEEE Signal Processing Letters,2013,20(9):861-864.
[3] Safizadeh M S,Latifi S K.Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accelerometer and load cell[J].Information fusion,2014,18:1-8.
[4] Angelov P,Yager R.Density-based averaging—A new operator for data fusion[J].Information Science,2013,222:164-174.
[5] Wei C M,Blum R S.Theoretical analysis of correlation-based quality measures for weighted averaging image fusion[J].Information Eusion,2010,11:301-309.
[6] Rodger J A.Toward reducing failure risk in an integrated vehicle health maintenance system:A fuzzy multi-sensor data fusion Kalman filter approach for IVH MS[J].Expert Systems with Applications,2012,39(10):9821-9835.
[7] Yang W B,Li S Y.A switch-mode information fusion filter based on ISRUKE for autonomous navigation of spacecraft[J].Information Eusion,2014,18:33-42.
[8] Ren Y E,Ke X Z.Multi-wavelet-basis multi-scale multi-sensor data fusion[J].Transducer and Microsystem Technologies,2010,29(9):77-79.
[9] Lv X Y,Gu X H.Eiltering algorithm for multi-microphones based on wavelet multi-scale information fusion[J].Chinese Journal of Science Instrument,2012,33(4):789-794.(in Chinese)
[10]Zhang J E,Smith J S,Wu Q H.Morphological undecimated wavelet decomposition for fault location on power transmission lines[J].IEEE Transactions on Circuits and Systems,2006,53(6):1395-1402.
[11]Lin Y,Yang Y D,Liu J.Eeature extraction methods of vibration signal in automobile main reducer based on morphological un-decimated wavelet[J].Journal of Agricultural Engineering,2010,41(2):209-214.(in Chinese)
[12]Huang B E,Shen L,Zhou X J,et al.Eault feature extraction of rolling element bearing based on morphological undecimated wavelet decomposition[J]. Journal of Agricultural Engineering,2010,41(2):204-207.(in Chinese)
[13]Sun Z H,Lv W Q.Signal analysis of rolling mill vibration based on morphological un-decimated wavelets and S-transform[J].Journal of University of Science and Technology Beijing,2013,35(3):366-370.(in Chinese)
[14]Higger M,Akcakaya M,Erdogmus D.A robust fusion algorithm for sensor failure[J].IEEE Signal Processing Letters,2013,20(8):755-758.
[15]Zhang L J,Yang J H,Xu J W,et al.Morphological undecimated wavelet and its application to feature extraction of impulsive signal[J].Journal of Vibration and Shock,2007,26(10):56-59.(in Chinese)
[16]Morenilla A J,Carmona R M,Romero J L S.Mathematical morphology for design and manufacturing[J].Mathematical and Computer Modeling,2011,54(7):1753-1759.
[17]Cousty J,Najman L,Dias E,et al.Morphological filtering on graphs[J].Computer Vision and Image Understanding,2013,117(4):370-385.
[18]Li B,Zhang P L,Wang Z J.Gear fault detection using multi-scale morphological filters[J].Measurement,2011,44(10):2078-2089.
[19]He W,Jiang Z N,Qin Q.A joint adaptive wavelet filter and morphological signal processing method for weak mechanical impulse extraction[J].Journal of Mechanical Science and Technology,2011,24(8):1709-1716.
[20]Hao R J,Chu E L.Morphological un-decimated wavelet decomposition for fault diagnostics of rolling element bearings[J].Journal of Sound and Vibration,2009,4(1):1164-1177.
[21]Wang B,Li H R,Xu B H.Motor bearing forecast feature extracting and degradation status identification based on multi-scale morphological decomposition spectral entropy[J].Journal of Vibration and Shock,2013,32(22):124-128.(in Chinese)
(Executive editor:Zhang Bei)
TH165 Document code:A Article ID:1005-1120(2015)03-0268-11
*CorresPonding author:Li Hongru,Professor,E-mail:lihr168@sohu.com.
How to cite this article:Sun Jian,Li Hongru,Wang Weiguo,et al.Morphological undecimated wavelet decomposition fusion algorithm and its application on fault feature extraction of hydraulic pump[J].Trans.Nanjing U.Aero.Astro.,2015,32(3):268-278.
http://dx.doi.org/10.16356/j.1005-1120.2015.03.268
(Received 4 January 2015;revised 5 April 2015;accepted 25 April 2015)
猜你喜欢
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Mechanical Behavior of Plastic PiPe Reinforced by Cross-Winding Steel Wire Subject to Foundation Settlement
- Ultrasonic ComPuted TomograPhy Imaging Method of Concrete Materials Based on Simulated Annealing Genetic Algorithm
- OPtimized Fuzzy Clustering Method for Health Monitoring of Shield Tunnels
- Low-Cost Wireless Sensor Network Node Design for Multi-Point Bolt Loosening Detection
- Modeling and Simulation of PiPeline Security Monitoring System Based on Line-Structure Sagnac Interferometer with 3×3 CouPler
- Data Fusion of MultiPle Curvature Mode ShaPes for Structural Damage Diagnosis
