Gyroscope Fault Diagnosis Using Fuzzy SVM to Unbalanced Samples

Luo Qiufeng（罗秋凤），Zhang Rui（张锐），Li Yong（李勇），Yang Zhongqing（杨忠清）

1.UAV Research Institute，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；

2.Department of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

whereφ（xi）is the mapping function from sample

Gyroscope Fault Diagnosis Using Fuzzy SVM to Unbalanced Samples

Luo Qiufeng（罗秋凤）1*，Zhang Rui（张锐）1，Li Yong（李勇）2，Yang Zhongqing（杨忠清）1

1.UAV Research Institute，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China；

2.Department of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

A novel fuzzy support vector machine based on unbalanced samples（ESVM-US）is proposed to solve the high false positive rate problem since the gyroscope output is susceptible to unmanned aerial vehicle（UAV）airborne electromagnetic environment and the gyroscope abnormal signal sample is rather rare.Eirstly，the standard deviation of samples projection to normal vector for SVM classifier hyper plane is analyzed.The imbalance feature expression reflecting the hyper plane shift for the number imbalance between samples and the dispersion imbalance within samples is derived.At the same time，the denoising factor is designed as the exponential decay function based on the Euclidean distance between each sample and the class center.Secondly，the imbalance feature expression and denoising factor are configured into the membership function.Each sample has its own weight denoted the importance to the classifier.Einally，the classification simulation experiments on the gyroscope fault diagnosis system are conducted and ESVM-US is compared with the standard SVM，ESVM，and the four typical class imbalance learning（CIL）methods.The results show that ESVM-US classifier accuracy is 12%higher than that of the standard SVM.Generally，ESVM-US is superior to the four CIL methods in total performance.Moreover，the ESVM-US noise tolerance is also 17%higher than that of the standard SVM.

fault diagnosis；gyroscope；fuzzy support vector machine（ESVM）；unbalanced samples；membership function

0 Introduction

Gyroscope is a key airborne sensor for unmanned aerial vehicle（UAV）［1］.It is reported that about 60%flight faults are associated with the gyroscope in an inertial navigation system. The gyroscope fault brings great risks into the flight safety of UAV.The main methods for sensor fault diagnosis are based on hardware redundancy，analytical redundancy，signal processing or artificial intelligence algorithmic techniques［2-6］.Support vector machines（SVM）is one of the artificial intelligence learning algorithms［7-8］，and it has been successfully applied to many real-world classification problems from various domains.The gyroscope fault datasets are far less than the normal datasets.In addition，the airborne gyroscope output signals are blended with noise signals or outlier from the UAV airborne complex electromagnetic environment where radio signals，engine working radiation，radar signals and radio interference signals often exist synchronously.Although SVM often deals effectively with balanced datasets，it could produce suboptimal results when faced imbalanced datasets. The SVM classification hyper-plane would shift to the minority（positive）dataset when it is applied to noises and unbalanced datasets［9］.Its classifi-cation accuracy greatly drops，and the majority（negative）dataset is over fitting.

Two main methods are addressed to solve the unbalanced dataset problem.One is based on the data preprocessing techniques such as over sampling，under sampling，and synthetic minority over sampling technique（SMOTE）［10-12］.The other is about the algorithmic modifications such as the kernel function improvement and different error costs（DEC）［13-15］.The SVM classification performance is enhanced to some degree when the number of the positive dataset and negative dataset is changed by resampling techniques，but the dataset structure and its integrity are damaged. Resampling techniques are adopted to tackle the imbalance problem between datasets，while it takes into few consideration the imbalance and noise problem within datasets.The fuzzy support vector machine（ESVM）algorithm is proposed in this paper to solve the number imbalance between datasets，dispersion imbalance within datasets，and noises from the UAV airborne electromagnetic environment when the imbalanced feature weights and denoising parameters are applied to the membership function.The gyroscope fault diagnosis system on fuzzy SVM for unbalanced samples is constructed.

1 SVM Algorithms

1.1 Standard SVM

SVM is a kind of classifier developed from statistical learning theory［7］.Eor a given dataset｛（x1，y1），（x2，y2），…，（xi，yi），…｝，where xi∈Rnrepresents an n-dimensional data point，yi∈｛-1，+1｝is a sample label.The goal of the SVM learning algorithm is to find a separating hyper plane that separates these datasets into two classes.According to the Mercer theorem，if the dataset is linearly separable，the optimal hyper plane can be transformed into a minimum target optimization problem asattribute to high-dimensional feature space，ξthe slack variable，parameter C the trade-off between training accuracy and generalization，ωthe weight vector that defines a direction perpendicular to the hyper plane of the decision function，b the bias that moves the hyper plane parallel to itself.

whereφ（xi）is the mapping function from sample

When an SVM classifier is trained using an imbalanced dataset，it can obtain a classification hyper plane bias toward the minority class.If the number between two class samples is roughly equivalent，the classification hyper plane will shift to the more scattered class.The classification hyper plane bias situation for imbalance dataset is shown in Eigs.1，2，where H is the classifier hyper plane，and H1，H2are the support vector planes.

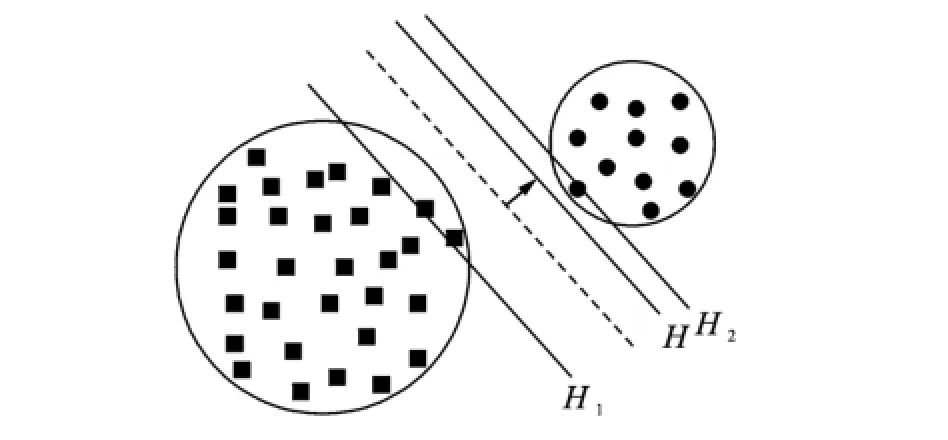
Eig.1 Bias situation for the number imbalance

Eig.2 Bias situation for the dispersion imbalance

1.2 Fuzzy SVM algorithm

Euzzy technology is applied to SVM to reduce the effect of noise samples（or outliers）on SVM classification［16］.According to the effect of each sample during the SVM training，each sample is given a different membership value.Assuming that each sample（xi，yi）is assigned a membership value si，the parameter S=｛（x1，y1，s1），（x2，y2，s2），…，（xi，yi，si）｝forms a fuzzy training set.After a nonlinear transformationφ: Rn→H is defined，input space can be transformed into high dimensional Hilbert space H，x→φ（x）. The problem of the optimal hyper plane for ES-VM model is deformed into the following optimization problems

where the membership si（i=1，2，…，l）represents the degree of training points（xi，yi，si）belonging to a certain class.The larger the value of siis，the less likely the corresponding samples are misclassified；and vice versa.

2 Fuzzy Membership Function Construction

The key of ESVM-US design is the construction of membership function.According to the working environment of the gyroscope，the design of membership function should solve two problems.One is to suppress the disturbance of noise and outlier in the class，and the other is to inhibit the imbalance of samples size and dispersion which affects the classification hyper plane shift.A membership function is represented by

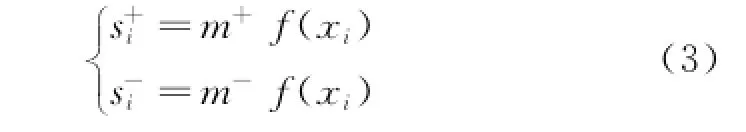
2.1 Imbalanced feature weight

Dispersion can be represented by the standard deviation of projection toωvector direction of classification hyper plane，the standard deviation of the positive class and the negative class samples point are

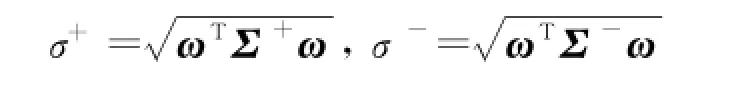
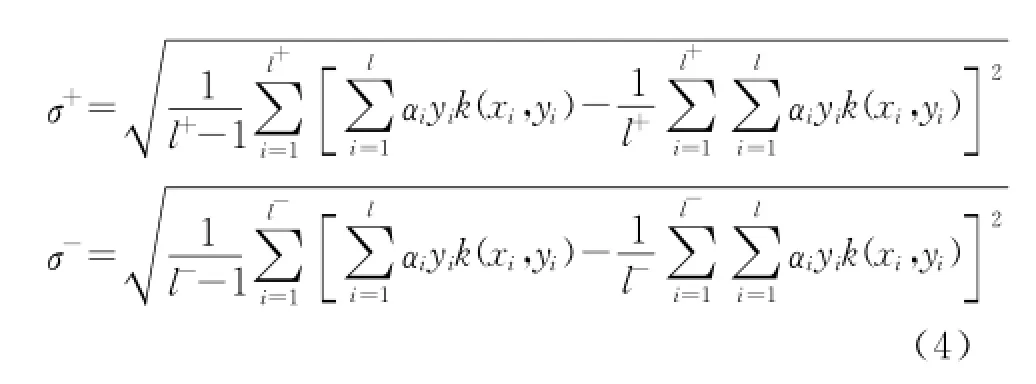
where∑+，∑-are the covariance matrixs of the positive and negative classes in high-dimensional Hilbert space，respectively；andφ（x）is a kernel function to substitute the dot product of mapping function.After initial training，SVM can obtain the vectorωof the classifier hyper plane.l+，lare the numbers of the positive class samples and negative class samples，respectively.To correct the offset caused by the different number of samples，the positive samples should be assigned higher weights than the negative ones.The weight is set inversely proportional to the number of samples.

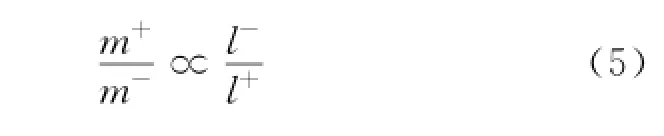
Besides，due to the classification bias toward the larger dispersion class，the larger dispersion class should have a higher weight.The weights of the dispersion imbalance within class can be set as

Einally the imbalanced feature weight is designed as

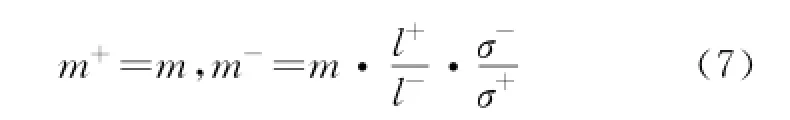
2.2 Denoising factor design

Denoising factor reflects the importance of sample within class.Assuming o1and o2are the centers of two class samples shown in Eig.3，respectively，obviously the sample x1and x2are away from their respective class center for noise properties.To reduce this noise interference，ESVM algorithm assigns a less weight for samples away from their center.

The Euclidean distance between samples and the class center is written as

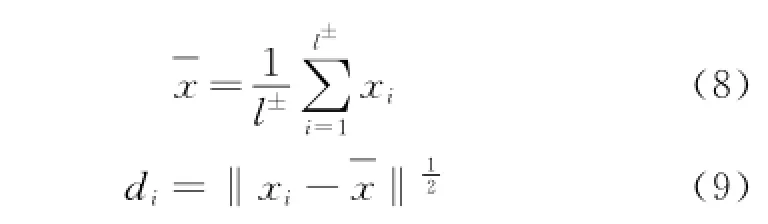
Then denoising factor can be calculated by the exponential decay function

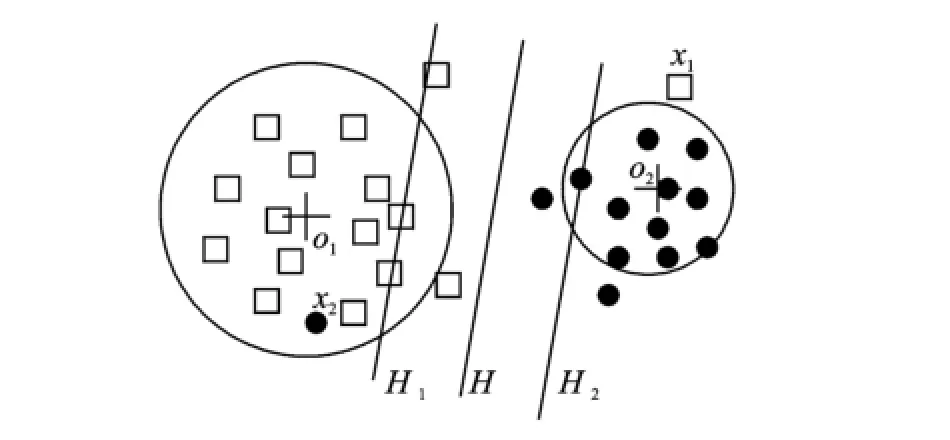
Eig.3 SVM classifier of noise pollution dataset

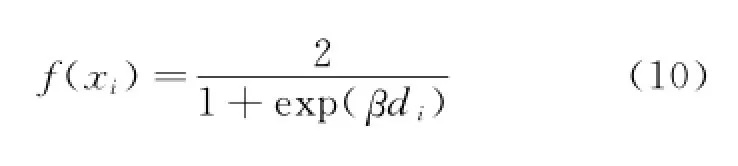
3 Gyroscope Fault Diagnosis System

3.1 Gyroscope signal feature extraction

Pitch angle output sample data are from the gyroscope in a certain UAV real flight with the signal sampling period of 20 ms.The main fault types of gyroscope include complete fault，constant bias fault，drift fault and periodic interference fault.The three-layer db4 wavelet method is used to decompose signal samples，and the corresponding frequency band energy as a feature vector is obtained.

3.2 Imbalance classification algorithm evaluation criteria

Generally，the accuracy rate of minority class samples as fault event attracts more attention in practice.The classifier generalization performance evaluation criteria for imbalanced dataset mainly take geometric means（g-means）metric and E-measure.A slightly improved g-means criteria is adopted in this paper since g-means criteria is used for the binary classification events. The gyroscope fault detection classification belongs to multi-classifier events.To reflect the imbalanced data classification，the four fault abnormal samples are regarded as a positive class.The confusion matrix of the dataset is shown in Table 1.

Table 1 Confusion matrix of dataset

In Table 1，TP，EP denote the correctly classified and misclassified numbers for positive samples，respectively.Likewise，TN，EN are defined for negative samples.The classification accuracy rate for positive samples is

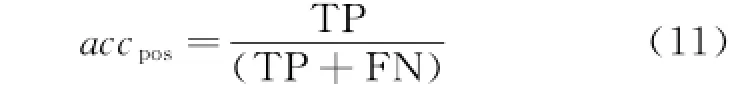
The classification accuracy rate for negative samples is defined as

Moreover，the geometric average is

3.3 Simulation

Classification program of SVM is compiled on Libsvm-weights-3.17 toolbox developed by Dr. Lin.The dataset imbalanced ratio is 5 with 400 sets of normal samples to 80 sets of each kind gyroscope fault sample.The kernel function in the experiment is Gaussian radial basis function k（xi，xj）=exp（-γ‖xi-xj‖2），and grid searching method and cross-validation method are synthesized to select the optimal kernel parameterγand penalty parameter C.The two-parameter optimization process is shown in Eig.4.

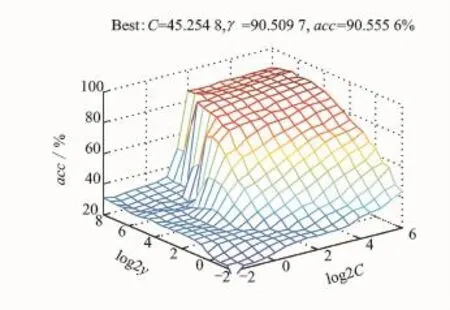
Eig.4 Parameter optimization process of grid searching method and cross-validation method

3.3.1 Standard SVM，ESVM and ESVM-US experiments

The classifier experiment of ESVM-US is conducted.Compared with standard SVM（SVC）and ESVM，the results are shown in Eig.5.

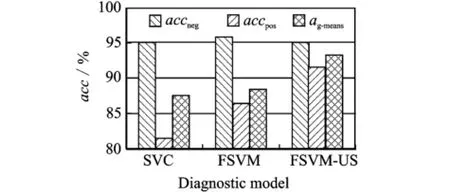
Eig.5 Experimental results of three diagnostic machines on unbalanced samples

Erom Eig.5，the performance of ESVM-US classifier is generally better than those of traditional ESVM and SVM，whose fault diagnostic accuracy rates are 81.4%and 86.4%，respectively.Highly unbalanced samples result in classifier hyper plane bias toward the minority class，and the minority class has a high misclassification loss.The fault diagnostic accuracy rate of ESVMUS reaches 91.5%，5%higher than that of the standard ESVM，and 10%higher than that of SVM approximately.The geometric average on ESVM-US is up to 93.2%，increases by appoximately 5.6%and 4.7%relative to the standard SVM and ESVM，respectively.The experiment results indicate that the ESVM-US can increase the diagnosis accuracy and weaken the classifier shift influence resulted from unbalanced dataset effectively.

3.3.2 Experiment on five-class imbalanced learning algorithms

The above experimental results show that the ESVM-US is superior to the standard SVM and traditional ESVM.With respect to the algorithms specially dealing with the unbalanced problem in Introduction，the advantage of ESVMUS is still not sure.Hence，several typical unbalanced learning algorithms，such as under sampling，over sampling，SMOTE and DEC，are compared with the algorithm proposed in this paper.The comparison results are shown in Eig.6.

In Eig.6，the five-class imbalanced learning algorithms obviously increase the classifier accuracy rate for fault samples compared with the standard SVM.The geometric average on ESVMUS algorithms is still 2%higher than the best one，SMOTE methods，and much higher than other class imbalanced learning algorithms.

3.3.3 ESVM-US noise tolerance capability experiment

Eig.6 Experimental results of five-class imbalanced learning

To verify noise tolerance capability of ESVM-US，one adds Gaussian white noise whose amplitude mean is 0，variance is 0.5 to signal samples of gyroscope.Different attenuation coefficientβin denoising fuzzy function is given as｛0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1｝.The results are shown in Eig.7.

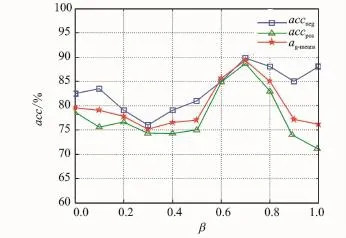
Eig.7 ESVM-US diagnosis results with differentβ

Eig.7 demonstrates that different attenuation coefficient has great influences on the diagnostic accuracy of the algorithm.Whenβis equivalent to 0.7，the ESVM-US performance is optimum. The gyroscope fault diagnosis experiment is performed on SVM，ESVM and ESVM-US under the condition ofβ=0.7.

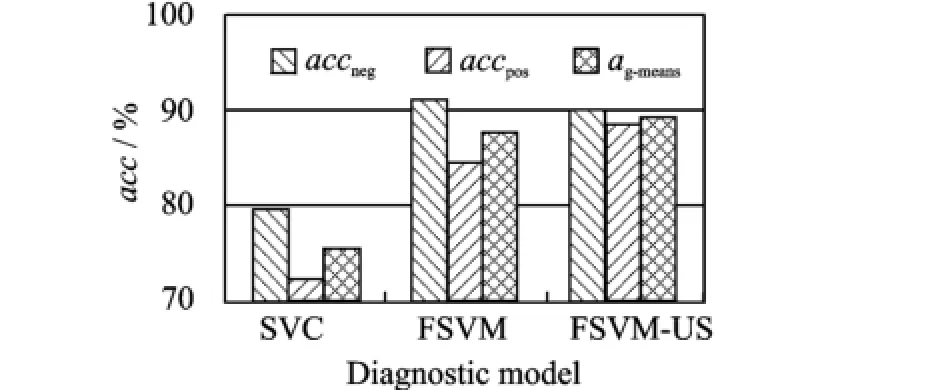
Eig.8 Results of three diagnosis models under noise condition

Erom Eig.8，the diagnostic accuracy of standard SVM is the worst，i.e.72.3%when noises are add-ed to the imbalanced samples，it is reduced by 10%relative to the one without noise.Luckily，the accuracies of the traditional ESVM and ESVM-US are 87.5%and 89.2%，only reduced by 1%—4%，compared with those in the situation without noise.

4 Conclusions

The classification accuracy of the traditional SVM is decreased because it is susceptible to the influence of noise pollution and unbalanced samples.ESVM-US algorithm is similar to most existing algorithms in considering of the sensitivity of classifier hyper plane to the quantity imbalance between negative and positive class samples.Moreover，it also considers the sensitivity to the dispersion imbalance with the same class samples，as well as the one to the noise pollution in trained samples.The experiment results show that the ESVM-US classification accuracy is improved obviously，and the proposed algorithm has strong robustness.Its fault accuracy performance has many advantages in general.

Theoretically，the gyroscope fault diagnosis system based on ESVM-US can sharply reduce the risk of UAV flight safety.The work on ESVM-US algorithm will be transplanted to hardware platform for the further investigation on its engineering practice.

Acknowledgement

This work was supported by the Eundamental Research Eund for the Central Universities（No. 56XZA12017）.

［1］ Guo Xiuzhong.Theory of gyro inertial navigation system［M］.Beijing:National Defence Industry Press，1996.（in Chinese）

［2］ Wang Xiaomeng，Zhang Ren.A sensor fault diagnosis method research based on wavelet transform and Hilbert-Huang transform［C］∥Eifth Conference on Measuring Technology and Mechatronics Automation.［S.l.］:IEEE，2013:81-84.

［3］ Mirzaee A，Salahshoor K.Eault diagnosis and accommodation of nonlinear systems based on multiplemodel adaptive unscented Kalman filter and switched MPC and H-infinity loop-shaping controller［J］. Journal of Process Control，2012（22）:626-634.

［4］ Zhu Daqi，Liu Yongan.Information fusion method for fault diagnosis［J］.Control and Decision，2007，22（12）:1321-1328.

［5］ Xiao Lizhi，Sun Dexiang，Liu Yuwei，et al.A combined method based on expert system and BP neural network for UAV systems fault diagnosis［C］∥2010 International Conference on Artificial Intelligence and Computational Intelligence.［S.l.］:IEEE，2010:3-6.

［6］ Zhang Yalin，Wei Min，Chen Pengzhang，et al. Overview on sensor fault diagnosis technology［J］. Transducer and Microsystem Technologies，2009，28（1）:4-12.（in Chinese）

［7］ Vapnik V.The nature of statistical learning theory［M］.New York:Springer Verlag，2000.

［8］ Yu Jun，Lou Peihuang，Wu Xing，et al.Automated guided vehicle cross path recognition based on rough set and hierarchical support vector machine［J］.Journal of Nangjing University of Aeronautics&Astronautics，2013，45（1）:62-69.（in Chinese）

［9］ Akbani R，Kwek S，Japkowicz N.Applying support vector machines to imbalanced datasets［C］∥15th European Conference on Machines Learning.Berlin: Springer Verlag，2004:39-50.

［10］He Haibo，Garcia E A.Learning from imbalanced data［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21（9）:1262-1284.

［11］Chawla N，Bowyer K，Kegelmeyer P.SMOTE: Synthetic minority oversampling technique［J］.Journal of Artificial Intelligence Research，2002（16）:321-357.

［12］Tao Xinmin，Liu Eurong，Tong Zhijing，et al.Novel fault detection method based on SVM with unbalanced datasets［J］.Journal of Vibration and Shock，2010，29（10）:8-12.（in Chinese）

［13］Veropoulos K，Campbell C，Cristianini N.Controlling the sensitivity of support vector machines［C］∥Proc Int Joint Conf Artif Intell.Stockholm，Sweden:［s.n.］，1999:55-60.

［14］Li Zhongguo，Hou Jie，Wang Kai，et al.Application of fuzzy support vector machine on road type recognition［J］.Journal of Data Acquisition and Processing，2014，29（1）:146-151.（in Chinese）

［15］Li P，Chan K，Eang W.Hybrid kernel machine ensemble for imbalanced datasets［C］∥Proceedings of the 18th International Conference on Pattern Recognition.［S.l.］:IEEE Computer Society，2006:1108-1111.

［16］Lin C E，Wang S D.Euzzy support vector machines［J］.IEEE Transactions on Neural Network，2002，13（3）:466-471.

（Executive editor:Zhang Tong）

V240；O321 Document code:A Article ID:1005-1120（2015）01-0016-07

*Corresponding author:Luo Qiufeng，Researcher，E-mail:yqwl2002@126.com.

How to cite this article:Luo Qiufeng，Zhang Rui，Li Yong，et al.Gyroscope fault diagnosis using fuzzy SVM to unbalanced samples［J］.Trans.Nanjing U.Aero.Astro.，2015，32（1）:16-21.

http://dx.doi.org/10.16356/j.1005-1120.2015.01.016

（Received 13 November 2014；revised 11 January 2015；accepted 12 January 2015）