基于遗传算法的中职排课系统设计与实现
2015-11-20王涛
王涛
摘 要:文章从排课系统研究现状出发,分析了影响排课问题的要素、条件与求解目标,采用基于遗传算法解决排课问题的框架,并设计了基于遗传算法的排课系统。
关键词:遗传算法;中等职业学校;排课系统
中图分类号:G640 文献标识码:A 文章编号:1002-4107(2015)11-0066-02
一、排课系统研究背景
在学校日常教学管理中十分重要,而又相当复杂的工作就是排课,其本质就是为学校的每一门课程及与其对应的教师安排时间和地点,从而使学校的日常教学工作能够有秩序地进行。
编排课程表是混合诸多因素的规划题目,要确保教师、学生、教室三者之间没有冲突,而且要考虑教师的实际需求及资源的局限等条件。
排课问题已经被证明是NP完全问题[1],是诸多学者研究的热点,研究者主要运用理论研究、启发式搜索、专家系统求解等方法来解决这个问题。近年来最多的是使用遗传算法来求解这个问题。
教学排课效率低满意度低是学校教务人员最头痛的问题,其最大的困难是硬件条件的局限。教务人员很难在同时兼顾硬件资源与软件资源的情况下快速编排任课教师、学生都满意的课表。
“穷举法”将所有的出路摆出,然后找到最佳的解决方案,但造价高,耗时长。如某一周有n个时间段可安排课时,有m个教师需要排课,这些教师每个星期要上i堂课,如果使用穷举法我们就可以得出一共有nm*i种组合结果,可见穷举法太繁复,不适合实际应用。
遗传算法是一种通过模拟自然进化过程搜索最优解的方法[2]。本文试图以遗传算法来实现排课问题的最佳解。
本课题研究的目的就是实现基于遗传算法的排课系统,满足日常教学需求。
二、遗传算法在排课系统中的应用
(一)排课问题描述
在排课问题中将各种因素有序地安排在一周的时间内且不发生冲突是我们的首要任务,这些因素包括班级、教室、课程、教师、时间。据此,我们给出如下描述。
学校有J间教室,B个班,K门课程,L位教师,S个时间段。
1.教室表述为J(J1,J2,…,Jn)集合,不同教室容纳的人数为(X1,X2…Xr)。
2.班级表述为B(B1,B2,…,Bn)集合,不同班级的人数为(K1,K2,…Kc)。
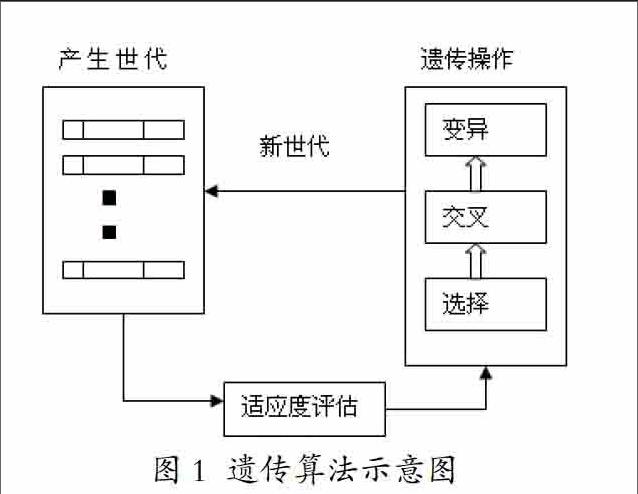
3.课程表述为K(K1,K2,…,Kn)集合,每门课对应Bi个班,1位教师,(1≤Bi 4.教师表述为L(L1,L2,…,Ln)集合,每位教师对应Km门课,Cn个班(1≤Km 5.时间表述为S(S1,S2,…,Sn)集合,一般情况下一周有五天上课,根据职业高中的实际情况每天为6节课,即上午4节,下午2节,则时间集合包含30个时间段。例如11代表周一第一节课,12代表周一的第二节课,21代表周二的第一节课,按此推导,这些课节构成一个时间集合P(11,12,13,…,56)。 (二)约束条件 1.一张正确的课表应至少满足以下硬约束条件。 (1)某一个教师、班级、教室在同一个时间节点内不能安排两门课程。 (2)教室必须容下上课的学生数,即Kc≤Xr。 2.硬性约束是必须满足的,否则教学无法正常进行 下去,但在实际教学当中为了使教学效果更好还应当有些软约束。这些条件在特殊情况下也可以不满足,这些软约束条件可能是: (1)把重要理论课程安排在上午进行,把动手课程安排在下午进行,这样符合学生的注意力规律。 (2)在满足学生上课时间要求的情况下尽可能满足教师对课程时间的要求。 (3)一门课要在一周的几个分散的时间段进行,就是说每周三课时的课不能安排在一天上完,也不能安排在相邻的三天上完,要使学生有时间预习消化,教师有时间备课批改。 (4)教师每天的课不能太多,否则影响教学效果。 (5)同第(4)条,学生上课时间不能一天是满课,一天又没有课的情况。 这些软性条件对于不同学校是不同的,笔者在这里列出的这些软性约束条件主要是针对中等职业学校的实际教学需要,在笔者的排课系统中,只是给我们定义的约束条件给出一个解决方案,如果有其他的要求就需要另外考虑[3]。 三、遗传算法分析 (一)遗传算法的循环过程 遗传算法的演算过程是模拟染色体交叉变异,生物进化淘汰的过程。 (1)随机产生一定数目的初始种群。 (2)评价个体适应度情况,如果个体符合适应度条 件,则个体代表的解可以使用,输出结果结束计算,否则转向下一步。 (3)依据适应度选择再生个体。 (4)按照一定的交叉概率和交叉方法生成新的个体。 (5)按照一定的变异概率和变异方法生成新的个体。 (6)由(4)和(5)产生新的种群,在判断适应度。如图1所示。 图1 遗传算法示意图 以下是遗传算法的伪代码。 BEGIN: I = 0; Initialize P(I); Fitness P(I); While(not Terminate-Condition) {I + +:GA-Operation P(I);Fitness P(I);}END. (二)染色体编码 在排课系统的实现过程中首先要解决的是将实际的课表变成虚拟的编码,就是如何将课表转化为染色体,使它可以进行遗传操作。在前人的方法中,常将染色体设计成浮点数或二进制编码,在实践中,将每个教师的课表设计成一个单独的染色体,结构如下面表述。
教师ID班级ID课程ID教室上课时间安排。
在本设计中染色体用十进制数来编码,例如:某一位教师编号为1234,要上“职业生涯规划”这门课,这门课的编号为7025,周学时为3,班级为01201、01202,上课时间是随机产生的,教室要选择大于两班总人数的,以此编码生成的染色体为:“12340120101202702502204
213451”其中02204代表上课教室,213451代表上课时间是周二第一节、周三第四节、周五第一节。
使用上面的编码方式,对染色体的后11位进行交叉操作,这样教师课程受影响,教师课表内含其他教师课程的情况都不会发生,也使得演化后的染色体编码更加合理。不过产生排课课表的优劣还需要适应度函数进行判断。
工作中适应度值就是课程编排人员对课表的期望。因此,把这些期望转化为具体数值就显得很重要,它是实现智能化的关键。
按照排课系统的要求,个体适应度评价函数的设计是一种奖惩并存的机制[4]。详细来说就是我们设计了奖励机制,比如教师在某个时间段上课比较方便,如果恰好有这么一个解,那么我们就奖励这个个体,该个体适应度值即加大了。相反惩罚(减去一个权值)的情况有,如果个体中有存在不满足硬约束的条件,那么就对该个体进行惩罚。有些解是我们不需要的,为了能够优先进化更好的解,因此它的适应度值需要降低。比如说在同一时间某个教师被安排了两门不一样的课在一个个体中,这就违反了硬约束条件;综合上述对排课多目标的分析,则采用以下适应度的函数:
fitness_value+reward_value-conflict_penalty_value=fitness
其中,reward_value表示奖励值,偏好设置根据教师偏好时间设置来指定分别为很满意(奖励+20)、还可以(奖励+10)、没有意见(奖励+0)、不满意(奖励-10)、非常不满意(奖励-20);fitness_value表示适应度的基础值,它是一个适应度函数的初始值,引入此值是为避免整体适应度值为负在基于奖惩模式情况下:Conflict_penalty_value代表冲突惩罚值,包含了任课教师与时间的冲突,教室和时间的冲突还有班级和时间的冲突,在相关类中该值的设定已经被指定。在自动排好的课表中如其中的安排符合教师的喜好,并是教师事先设定好那么就直接对相应的结果进行奖励相应的值,就是说结果适应度值的高低,取决于教师是否满意。以此类推不符合教师期望的教师不满意,它的适应度值自然就低。如果在程序中出现班级在同一时间上多门课的情况、教师同一时间上多门课的情况、教室同一时间多班级使用的情况、教室类型与课程需要不符合的情况,这些都需要设定相应的惩罚值,在适应度上减去相应的值。确保这样的结果不会出现在生成的课表上。
排课系统的设计使用了前台界面操作与后台数据库处理相结合的方式。使得日常的管理操作和数据库中数据的存储相区分开来,使得两者不会发生错误的干扰,增加了各个用户的独立性。这样的结构给软件的开发和维护带来了方便。
由于本系统尚在完善阶段,存有瑕疵,如在安全性能方面,在线共享方面等。这也激励笔者在今后的学习工作中要逐步地完善提升。排课系统为保证以优质的课表供师生使用,仍需严格的测试。
参考文献:
[1]吴金荣.解课程表问题的分支定界算法[D].北京:中国
科学院数学与系统科学研究院,2002.
[2]胡顺仁,邓毅,王铮.基于高校排课系统中的图论问题研
究[J].计算机工程与应用,2002,(4).
[3]刘继清,陈传波.模拟退火算法在排课中的应用[J].武
汉船舶职业技术学院学报,2003,(6).
[4]李增智,王云岚,陈靖.课程表问题的一种混合型模拟退
火算法[J].西安交通大学学报,2003,(4).
