例析分层次教学在高中数学课堂中的应用
2015-11-20潘丽钦
潘丽钦
(福建省清流县第一中学)
例析分层次教学在高中数学课堂中的应用
潘丽钦
(福建省清流县第一中学)
新课程改革要求在教学中必须确立面向全体的教育思想。面向全体与注重个别差异进行分层教学符合新课程标准理念,通过几个例子分析分层次教学在高中数学课堂中的应用。
分层次教学;正确分层;应用
一、简述分层次教学
分层次教学是根据班级的具体学情,以班级学生能接受的程度为基础,确定一节课知识的教学起点、教学量、教学进度,精心设计教学方案,因人施教。区别对待、分层施教、全员参与、共同进步,这样既能保证每个学生都能达到基本要求,又能因人而异使每个学生的个性得到发展,使不同层次的学生都参与到教学过程中来,实现学生学习的个体化、最优化,使学生真正成为学习的主人。
二、分层次教学的理论依据
人的认识,总是由浅入深,由表及里,由具体到抽象,由简单到复杂的。教学活动是学生在教师的引导下对新知识的认识活动,数学教学中不同学生的认识水平存在着差异,因而必须遵循人的认识规律进行教学设计。分层次教学中的层次设计,就是为了适应学生认识水平的差异,根据人的认识规律,把学生的认识活动划分为不同的阶段,在不同的阶段完成适应认识水平的教学任务,通过逐步递进,使学生在较高的层次上把握所学的知识。
三、例析分层教学在高中数学课堂中的应用
(一)分层教学在集合中的应用
例1.问题1:已知集合A={1,2,3},B={1,a+2},若B⊆A,求a的值。
解:∵B⊆A,∴a+2=2或a+2=3,解得a=0或a=1.经检验a=0或a=1均满足题意。
问题2:已知集合A={1,a2,3},B={1,a+2},若A∪B=A,求a的值。
解:∵A∪B=A∴B⊆A
若a+2=a2解得a=2或a=-1,经检验a=-1不符合题意,故a=2.
若a+2=3解得a=1,经检验a=1不符合题意。
综上所得a=2。
注:问题1是对集合的简单应用;问题2是问题1的升华,综合性更强。本题涉及分类讨论的思想。从问题1到问题2,分层明显,使每个层次的学生都能获得成功的体验。
(二)分层教学在函数中的应用

(1)若t=1,求(fx)的单调增区间;
(2)若(fx)在区间[-1,1]上是增函数,求t的取值范围.
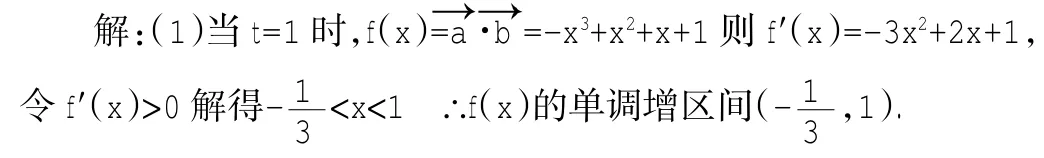
(2)由题知(fx)=x(21-x)+(x+1)t=-x3+x2+tx+t
∴f′(x)=-3x2+2x+t.若(fx)在区间[-1,1]上是增函数,
则有f′(x)≥0⇔t≥3x2-2x在[-1,1]上恒成立.
在区间[-1,1]上,g(x)max=g(-1)=5,故在区间[-1,1]上使t≥g(x)恒成立,
只需t≥g(-1)即可,即t≥5.故t的取值范围是[5,+∞).
注:对于(1),已知函数求单调性,大部分学生都会做。而(2)是已知函数的单调性求参数的取值范围,难度有所提高,从(1)到(2)分层明显,使各层次的同学都有所得。
(三)分层教学在不等式中的应用
例3.问题1:解不等式x2-2x-3<0
解:因为Δ=(-2)2-4×1×(-3)=16>0,方程x2-2x-3=0的解是x1=3,x2=-1所以不等式x2-2x+3<0的解集是{x|-1<x<3},
问题2:解不等式x2-5ax+6a2>0,(a≠0)
解:原不等式可化为:(x-2a)(x-3a)>0,对应方程(x-2a)(x-3a)=0的两根为x1=2a,x2=3a。
当a>0时,即2a<3a,解集为{x|x>3a或x<2a};
当a<0时,即2a>3a,解集为{x|x>2a或x<3a}。

注:对于问题1,2大部分学生还是会理解,但是问题3中两个大小就不容易比较出来。本例题体现了分类讨论的思想。从问题1 到3层次明显,达到了分层次教学的目的。
(四)分层教学在解析几何中的应用
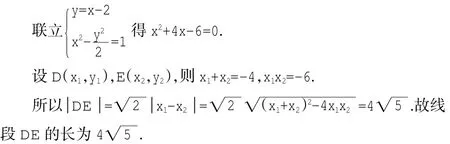
问题2:已知抛物线y2=2px(p>0).过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A,B.若AB ≤2p,求a的取值范围.
解:直线l的方程为y=x-a,将y=x-a代入y2=2px,
得x2-2(a+p)x+a2=0.
设直线l与抛物线的两个不同交点的坐标为A(x1,y1)、B(x2,y2),

注:利用弦长公式问题1就迎刃而解,问题2的直线不仅含参数而且与不等式结合,难度明显提高,从问题1到问题2体现了分层次教学。
(五)分层教学在三角函数中的应用
例5.问题1:在△ABC中,若a2=b2+c2-bc,则A=().
解:∵a2=b2+c2-bc
问题2:在△ABC中,若(a+b+c)(c+b-a)=3bc,
(1)求角A.
解:(1)∵(a+b+c)(c+b-a)=3bc,∴a2=b2+c2-bc
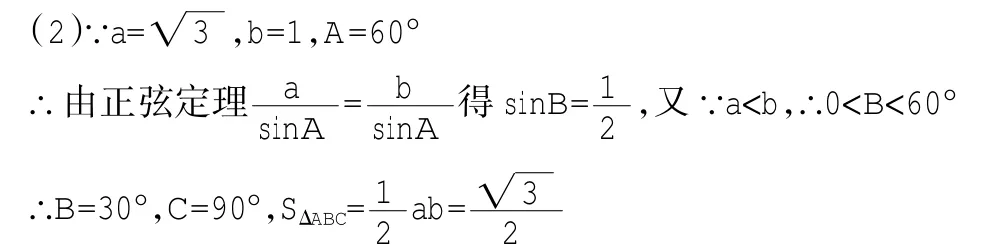
注:问题1只要适当引导学生就容易想到应用余弦定理来解决,但是问题2学生看到式子(a+b+c)(c+b-a)=3bc就怕了,不知道怎么化简,更不用讲会利用正余弦定理来解决。从问题1到问题2,层次明显,会使不同层次的学生各有所得。
(六)分层教学在立体几何中的应用
例6.问题1:在长方体ABCD—A1B1C1D1中,若AA1=2,AB= AD=1,则该长方体外接球的表面积为__。答案:6π
问题2:三棱锥P-ABC的四个顶点点在同一球面上,若PA⊥底面ABC,底面ABC是直角三角形,PA=2,AC=BC=1,则此球的表面积为__。答案:6π
注:对于问题(1)大家比较容易求出长方体外接球的半径,对于问题(2)只要把三棱锥P-ABC放进长方体里就跟问题(1)一样了,从而将问题简化.从问题1到2层次明显,达到了分层教学的目的。
四、分层次教学的反思
采用分层教学后,出现了“你追我赶,奋勇向前”的可喜局面。对于层次较低的学生,因为学习目标定得较低,学习过程中又能得到老师更多的帮助,从而增强了学习的信心和战胜困难的勇气。对于层次较高的学生也因难度的加大而有所得。
总之在普通高中数学教学中正确地运用“分层次教学”,可使学生的学习目的性更明确,自觉性更强,学习兴趣更浓厚,达到缩小两极分化,大面积提高数学教学质量的目的。
[1]孙金义.新课标下对分层教学的尝试.科学教育,2009 (15):13-14.
[2]韩德宗.新课改背景下的“分层递进教学”初探.中国教师, 2012(04).
·编辑 郑淼
