钢骨－钢管高强混凝土偏心受压柱非线性分析

关萍，陈兰响，刘晴晴

（1.大连大学 建筑工程学院，辽宁 大连116622；2.沈阳建筑大学 土木工程学院，辽宁 沈阳110168）

钢骨－钢管高强混凝土组合柱（STSRHC）充分利用了钢管混凝土和钢骨混凝土各自的力学性能，具有承载力高、刚度大、抗震性能和动力性能好、构件截面尺寸小等优点，有望在高层房屋、高耸结构、桥梁结构、地下结构等中得到应用.2003年，赵大洲等［1－3］相继对这种组合柱进行了理论和试验研究，并取得了一定的成果.目前，对钢骨－钢管混凝土柱的力学性能理论研究和实际应用研究还处于研究阶段.实际工程中的组合柱大多处于压弯受力状态，为满足工程设计的需要，本文拟利用有限元软件ABAQUS对钢骨－钢管高强混凝土偏心受压柱的力学性能进行研究.

1 有限元模型

1.1 应力－应变关系模型

核心混凝土本构模型在ABAQUS软件中采用塑形损伤模型［4－5］，拟采用王连广［6］的受压应力－应变关系式，并考虑偏心距对核心混凝土本构的影响［7］，最终提出的受压应力－应变关系模型，即

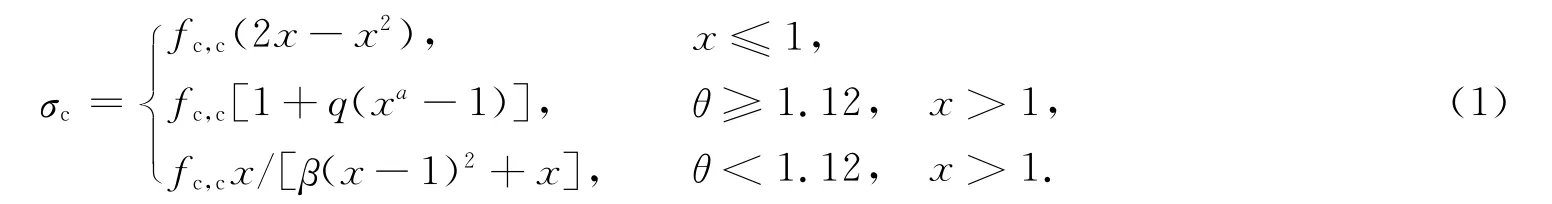
式（1）中：x＝ε／ε0；σc为混凝土压应力；fc，c为核心混凝土抗压强度；β，q和a为待定参数.

各参数的取值为

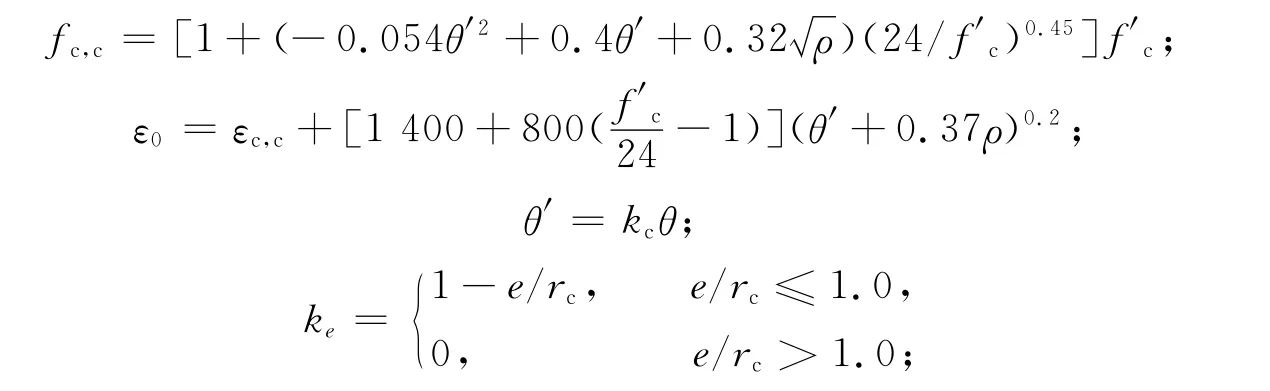
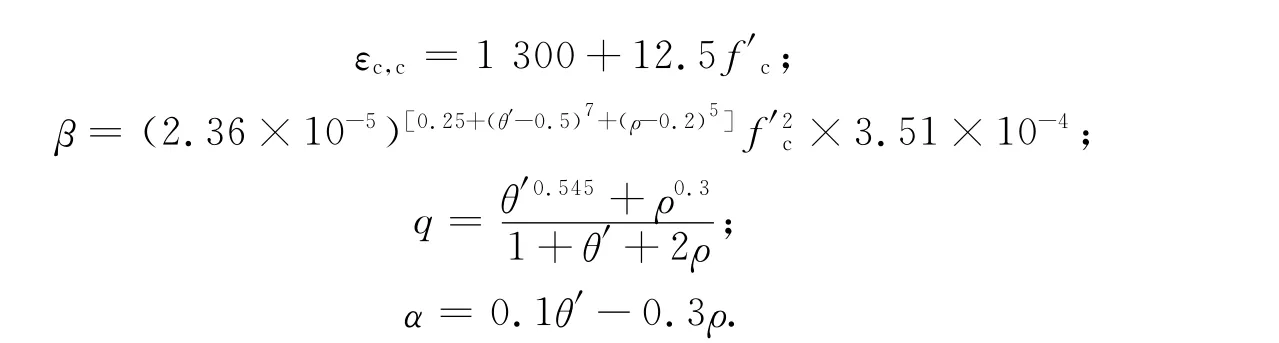
上式中：θ＝Atft，y／Atft为套箍率；θ′为修正套箍率；e为偏心距；ke为径向应力梯度函数；ρ＝Asfs，y／Acfc为配骨指标；At，As和Ac分别为钢管、钢骨和混凝土的面积；ft，y，fs，y，fc和f′c分别为钢管屈服强度、型钢屈服强度、混凝土轴心抗压强度和混凝土圆柱体抗压强度；εc，c为fc，c所对应的混凝土压应变.

混凝土受拉的应力－应变关系模型及钢材的材料模型采用文献［8］提供的模型.

1.2 单元选取和网格划分

考虑到收敛性和准确性，加载板、钢管、钢骨和混凝土均采用8节点减缩积分格式的三维实体单元（C3D8R）.拟采用细化网格的方式对网格的收敛性进行分析，当计算停止时，重新调整网格密度以提高收敛性.各部件的单元划分示意图，如图1所示.

图1 钢骨－钢管混凝土有限元模型和加载方式Fig.1 Finite element model and loading form of STSRHC

1.3 接触面处理和边界条件

钢管与混凝土之间的法向接触采用“硬”接触，界面切向力模型采用库伦摩擦模型［9］，摩擦系数为0.6；其他部件的接触采用“Tied”接触，并采用位移加载方式，利用增量迭代法求解方程；构件的边界条件如图1（d）所示.

2 计算值与试验值

选用文献［1］中的试件HL、文献［10］中的SE1，SE2和SE5和文献［11］中的LE1为参考构件，构件的参数、试验结果值和有限元计算结果，如图2所示.图2中：D为钢管直径；t为钢管壁厚度；L0为构件计算长度；λ为长细比，λ＝4L0／D.

由图2可知：计算值与试验值整体吻合良好.出现误差的主要原因是试验中构件的实际边界条件和材料很难与有限元模型完全符合.

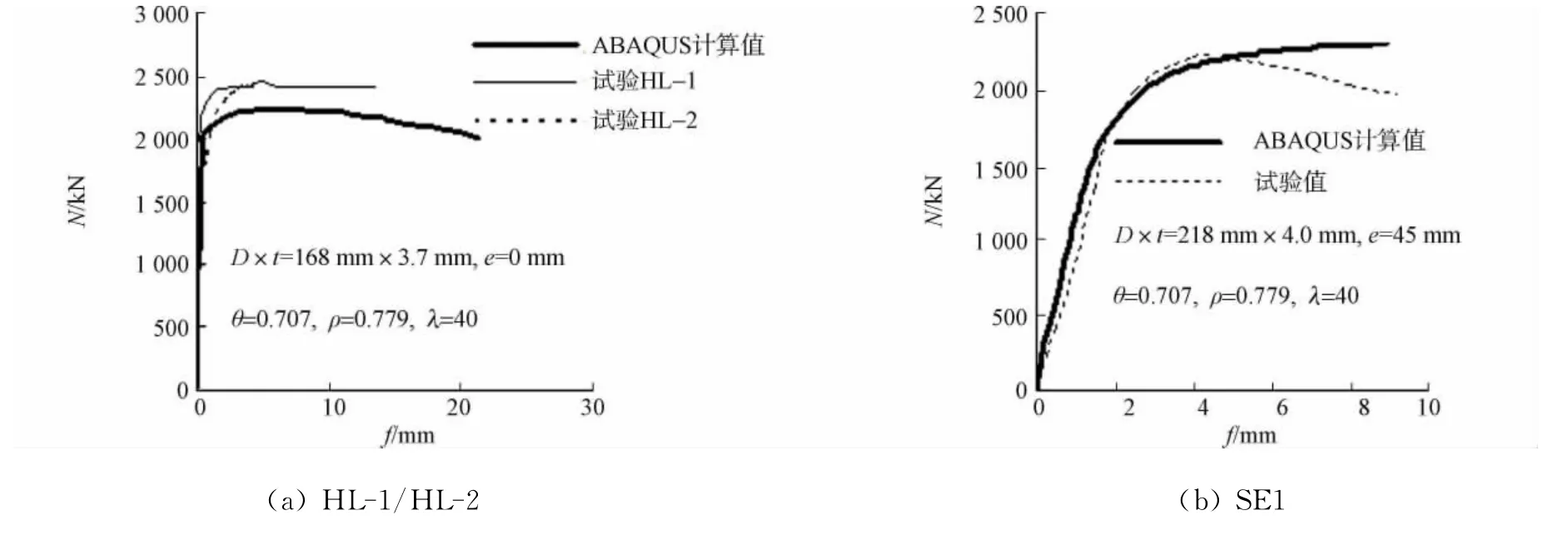
图2 承载力数值计算值与试验值比较Fig.2 Comparisons between calculation results and experimental results

3 参数分析

选用试件HL为参考构件，分别改变偏心距（e）、长细比（λ）、套箍指标（θ）、配骨（ρ）和混凝土强度（fc，u），分析各参数对其压弯力学性能和承载力的影响，结果如图3所示.当分析钢骨截面指标（Is／Ic）对其压弯力学性能和承载力的影响时，选取的构件参数为D×t×L0＝308mm×4mm×3 850mm，θ＝0.381，ρ＝0.722，结果如图3（f）所示.图3中：Is为钢骨截面惯性矩；Ic为混凝土截面惯性矩.由图3可以得到以下5点主要结果.

1）偏心距对偏压柱的力学性能和承载力影响最为明显.随着偏心距增大，承载力下降幅度较大，侧向挠度在承载力一定情况下明显增大.这主要是由于随偏心距的增加，全截面由全部受压逐渐变为部分受拉，而核混凝土的抗拉作用较小，受拉部分混凝土提前破坏，承载力逐渐降低.因此，钢骨－钢管混凝土并不适合作为大偏心受拉构件使用.

2）长细比对偏压柱的力学性能和承载力的影响也相对较为显著.随长细比增加，偏压柱的挠度增长较快，承载力下降也较为明显，这主要是由于组合柱的失稳导致的.

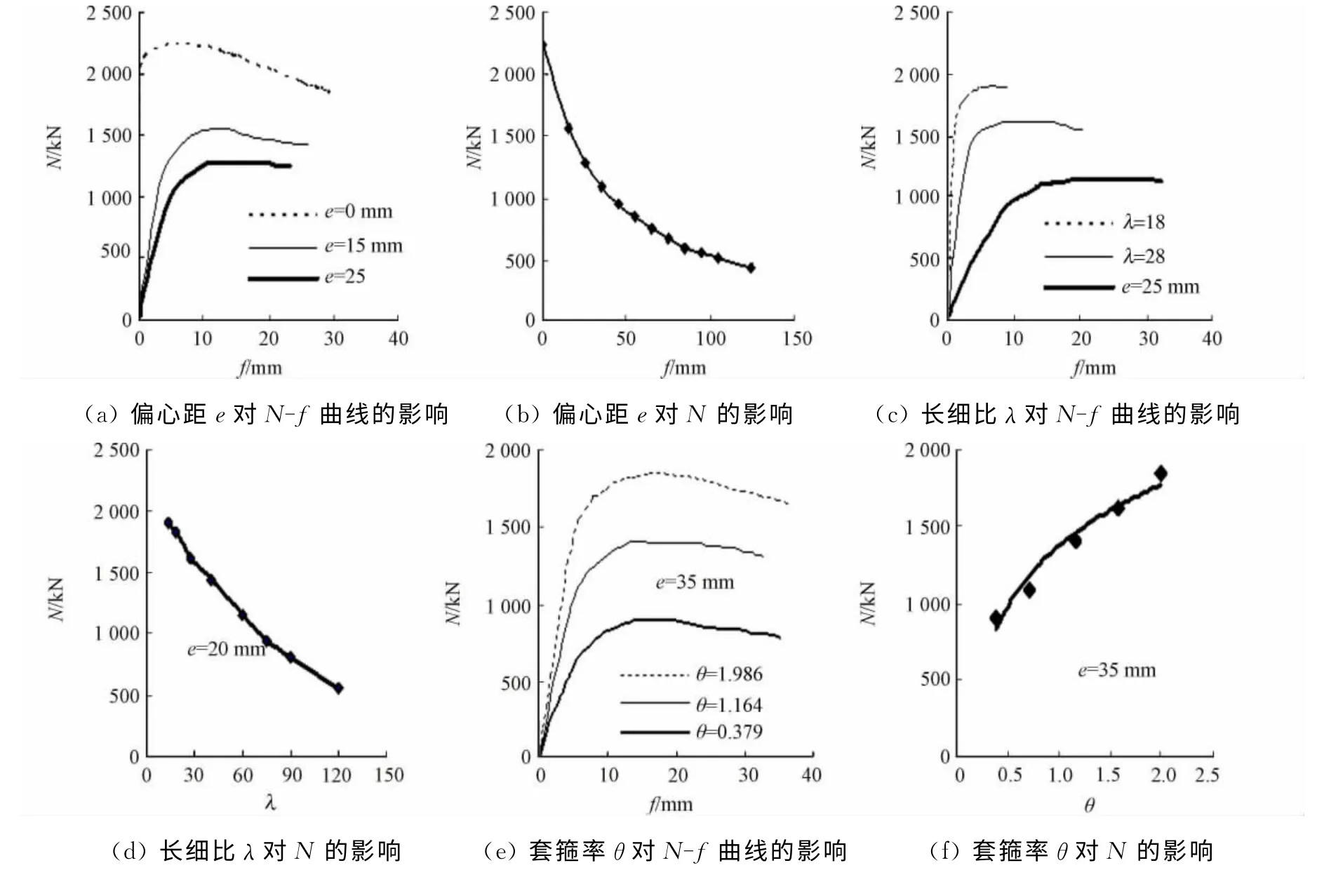
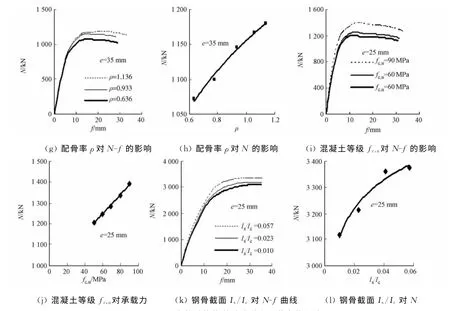
图3 不同参数对荷载－挠度曲线和承载力的影响Fig.3 Influence of different parameters on load－deflection and bearing capacity

3）套箍率和配骨率对偏压组合柱的力学性能和承载力有一定程度影响.承载力随着这两个指标的增大而增大，且套箍率的影响幅度相对配骨率较为明显.这主要是由于钢管对混凝土有一定程度的约束，混凝土受约束后，其承载力得到提高，且钢管的截面惯性矩较大，钢管的抗弯承载力相对钢骨较高.

4）混凝土强度在偏心距相对较小时，对组合构件的力学性能和抗弯承载力有一定影响，极限承载力和抗弯刚度随混凝土等级的提高而逐渐变大.

5）钢骨的截面形式对偏压柱的影响幅度相对较小，但随着其截面惯性矩的增加，组合构件的承载力也相应提高.这主要是由于惯性矩增加可以提高抗弯承载力，延缓混凝土受拉破坏，构件整体受压承载力得到提高.

4 承载力计算方法

《钢管混凝土结构设计与施工规程》采用经验系数法给出钢管混凝土柱偏心受压承载力公式，《钢－混凝土组合结构设计规程》采用了轴力－弯矩相关关系法给出钢管混凝土的偏压承载力公式.文中采用钢管混凝土承载力计算方法，推导钢骨－钢管混凝凝土组合柱偏压承载力公式.

4.1 经验系数法

采用经验系数法［8］得出组合柱的压弯承载力式Nu，有

式（2）中：N0为钢骨－钢管混凝土轴压短柱承载力计算值；φl 为长细比影响系数；φe 为偏心率影响系数；K为偏心率对紧箍力的影响系数.

短柱轴压承载力公式和各系数的取值分别为

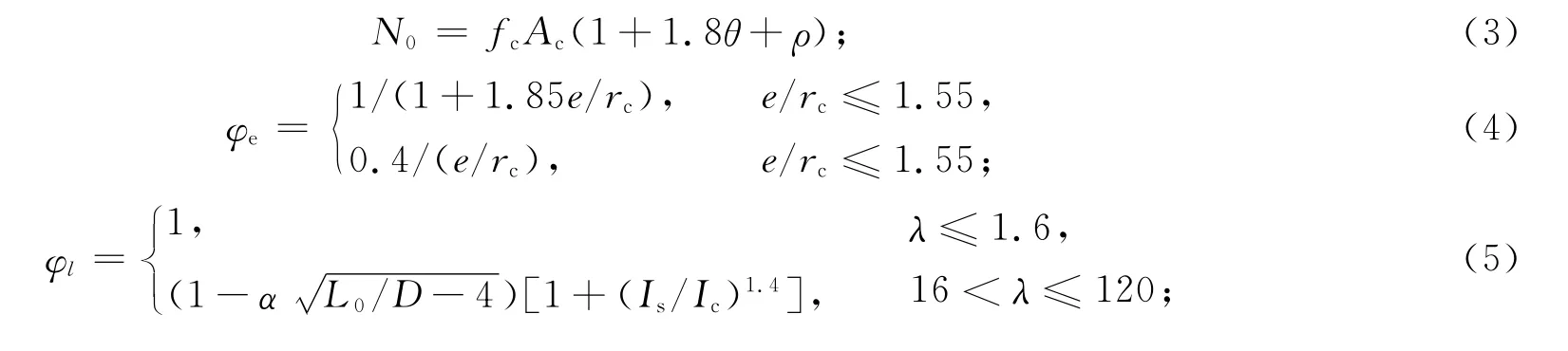
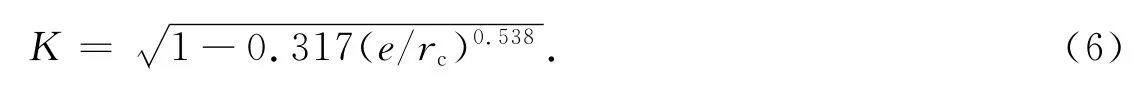
式（3）～（6）中：rc为钢管的内径；长细比限制在120以内，满足工程中柱的长细比范围（一般为20～80）；α为与长细比大小有关的参数.各参数取值，如表1所示.

表1 α，λ取值Tab.1 Values ofαandλ

为验证公式的正确性，选取文献［10－11］的试验值与经验公式法计算值进行对比，结果如图4所示.

比较结果可知，简化公式计算值与试验值吻合良好（计算值与试验值比值的平均值为0.958，均方差为0.058），且偏于安全.

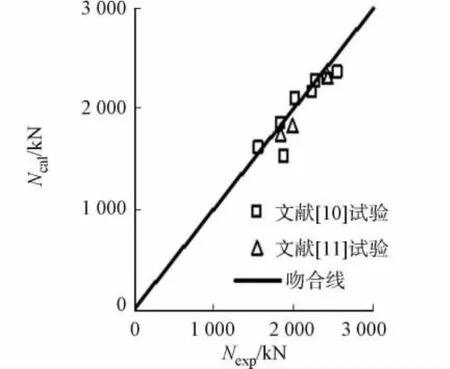
图4 承载力计算值与试验值的比较Fig.4 Comparison of experimental and calculated results on ultimate bearing capacity

4.2 轴力－弯矩相关关系法

从安全和实用的角度出发，可将N／N0（η）－Mu／M0（ξ）曲线关系简化为二折线模型［11］，模型如图5所示.图5中：N为实测压弯承载力，Mu为构件在偏心荷载下的抗弯承载力；η和ξ分别为N／N0和Mu／M0的简化值.模型方程为

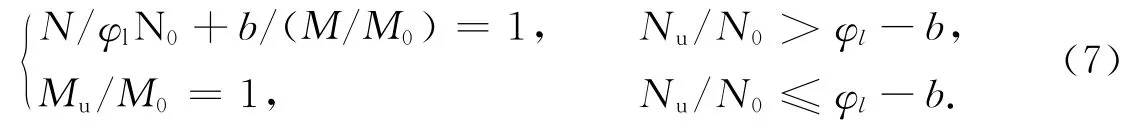
式（7）中：b＝0.315＋0.58exp；Mu为弯矩；M0为构件纯弯承载力［12］，M0＝rmWs，c，sfs，c，s，rm为塑形发展系数，rm＝（－0.404 7θ＋1.70）［－0.40＋1.110ρ－0.847ρ2）（Is／Ic）0.056］，Ws，c，s为 构件的 截面抵抗矩，Ws，c，s＝πD3／32，fs，c，s为构件的屈服强度，fs，c，s＝（1.392＋Bθ＋Cθ2＋Eρ）fc，D为钢管的直径；B，C，E为与材料强度的有关参数，B＝0.175 9ft，y／235＋0.974，C＝0.030 9－0.103 8fc／20，E＝0.156fs，y／235＋0.479.

为了验证公式的正确性，选取文献［10］中试件SE1，SE2和SE3，以及文献［11］中试件LE1和LE2为参考构件，验证结果如图6所示.由图6可知：试验结果、有限元结果和基于相关关系法建立的简化公式计算结果整体吻合良好.

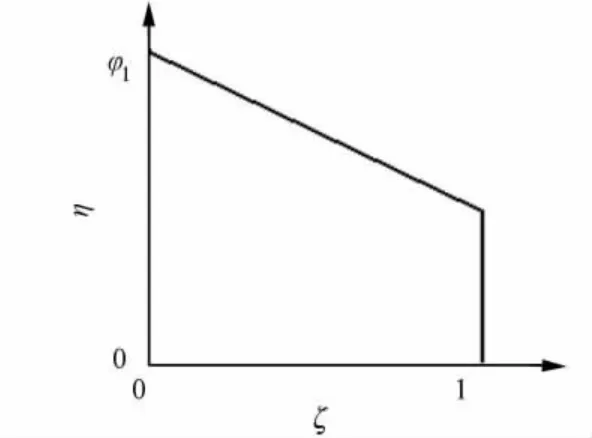
图5 N／N0（η）－M／M0（ξ）曲线Fig.5 Curve of N／N0（η）－M／M0（ξ）

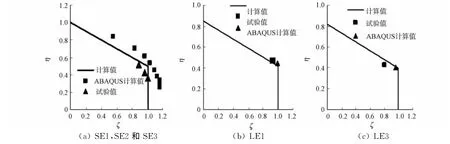
图6 简化公式的验证Fig.6 Validation of the simplified formula

5 结论

综上研究，可得出3点结论.

1）通过选择合理的力学模型，利用ABAQUS有限元软件对钢骨－钢管高强混凝土偏压柱的力学性能和承载力进行分析，所得计算结果与试验结果整体吻合良好.

2）对影响偏压柱的力学性能和承载力的因素进行分析，偏心距和长细比是影响其力学性能和承载力的关键因素.

3）通过有限软件进行的数值分析和参考以往的研究成果，基于经验系数法和轴力－弯矩相关系数法，分别建立钢骨－钢管混凝土偏压柱极限承载力简化公式，其计算结果与试验结果吻合较好.

［1］赵大洲.钢骨－钢管高强度混凝土组合柱力学性能研究［D］.大连：大连理工大学，2003：1－46.

［2］关萍，王清湘，赵德深.钢骨－钢管混凝土组合柱压弯性能试验研究［J］.辽宁工程技术大学学报：自然科学版，2003，22（3）：329－332.

［3］王连广，刘晓，常江.钢管钢骨高强混凝土偏心受压承载力试验研究［J］.工程力学，2010，27（2）：124－129.

［4］LEE J，FENVES G L.Plastic damage model for cyclic loading of concrete structures［J］.Journal of Engineering Mechanics，1998，124（8）：892－900.

［5］LUBLINER J，OLIVER J，OLLER S，et al.A plastic－damage model for concrete［J］.International Journal of Solids and Structures，1989，25（3）：299－329.

［6］王兵，王连广，刘晓.钢管钢骨轴压短柱受力全过程分析［J］.沈阳建筑大学学报：自然科学版，2009，25（1）：128－132.

［7］SUSANTHA K，GE H，USAMI T.Uniaxial stress－strain relationship of concrete by various shaped steel tubes［J］.Engineering Structures，2001，23（10）：1331－1347.

［8］韩林海.钢管混凝土结构：理论与实践［M］.北京：科学出版社，2007：1－300.

［9］张岩，张安哥，陈梦成，等.圆钢管混凝土轴压长柱有限元分析［J］.哈尔滨工业大学学报：自然科学版，2007，39（增刊1）：94－98.

［10］杨山波.钢骨－钢管混凝土偏压短柱承载力试验研究［D］.长沙：湖南大学，2009：1－52.

［11］澎丽纯.钢骨－钢管混凝土偏压长柱承载力试验研究［D］.长沙：湖南大学，2009：1－60.

［12］陈兰响，关萍.基于分层组合法推导钢骨－钢管高强混凝土纯弯承载力［J］.水利与建筑工程学报，2015，13（1）：51－55.