户外噪声相干预测模型及其工程应用

阮学云，魏浩征，李志远（1.安徽理工大学机械学院，安徽 淮南 3001；.合肥工业大学噪声与振动工程研究所，安徽 合肥 30009）

户外噪声相干预测模型及其工程应用

阮学云1，2*，魏浩征2，李志远2（1.安徽理工大学机械学院，安徽 淮南 232001；2.合肥工业大学噪声与振动工程研究所，安徽 合肥 230009）

基于几何衍射理论、相干虚源法等理论方法，提出一种适合于工程算法的户外噪声相干预测模型.该相干预测模型不仅能计算声源在经过有限长声屏障或多重声屏障时，由于多条路径衍射声形成的相干声场，还可计算声源在屏障等界面之间经多次反射后，多个反射声形成的相干声场.应用该相干预测模型对某变电站电力变压器周围的相干声场进行预测，通过与ISO9613-2标准算法、边界元法与实测值进行对比，结果表明，该户外噪声相干预测模型能反映出声波在不同位置处的波动性，比原有的ISO9613模型更接近测试结果，证明了所提理论模型的有效性，可应用于大范围的户外噪声预测计算.

相干声场；噪声预测模型；衍射声；反射声；相干虚源法；工程算法

工业企业中如电厂、水泥厂等大型工程建设项目，在进行声环境影响评价工作时需要进行大规模的辅助计算，目前国内企业多进口国外的通用噪声预测软件，如SoundPlan、Cadna/A等.而这些通用的户外噪声预测软件均基于ISO9613-2标准［1］，该标准前提条件就是基于互不相干声源的能量叠加.然而在对某些工业企业如高压直流换流站进行现场测试时发现，换流站内各主要噪声源相同设备（如电容器、换流变压器等）数量众多，且邻近布置，工作时噪声辐射特性相同，因此存在大量相干声源.由于目前ISO9613-2标准不考虑激励声源的相位信息，不仅对于不同声源之间可能存在的干涉影响无法计算，而且对于同一声源在传播过程中，由于有限长屏障作用引起的多路径衍射声或由各反射面组成半开空间内的多次反射声组成的相干声场也不予考虑，因此针对声源经过多重反射和多个衍射路径到达的声场区域，其预测结果往往误差较大.

点声源的户外辐射传播特性研究是研究户外声传播的核心基础，依据其理论基础可分为基于声场波动性的预测方法、几何声学预测模型，以及试验和半经验方法.户外噪声传播中，由于声线遇到障碍物和反射体会产生大量的衍射声和反射声，因此基于声场波动性的预测主要是针对屏障的衍射和反射问题进行研究.波动理论作为经典方法最早主要用于计算室内声场［2］.该理论是严格准确的解析方法，目前仅在具有规则形状的空间中才较容易实施.声场波动方程包含两个部分：一个对空间体积的积分，用于计入空间所有声源的直达声贡献；和一个对空间所有边界的面积分，用于计入边界对声场的散射贡献.而对后者使用数值方法加以离散计算，即为边界元法的基本原理［3-4］.基于几何声学的计算方法，是声场预测模型中最为简便的方法，最早用于计算室内声场，计算复杂度相对不高，且适用场合最为广泛［5-6］.在研究衍射声场时，最早由Keller提出了几何衍射理论（简称GTD）来描述声衍射［7］.在研究反射声场时，1972年Gibbs和Jones首次提出使用虚声源法模拟室内声场.之后，Kuttruff等在此基础上研究类似空间声能量分布，但这些模型都没有考虑考虑闭空间中各面反射声波间的干涉现象，适用于空间中宽频带的声场能量估计［8-10］.但实际空间中，声场的空间和频率分布通常是起伏不定的，各面反射的声波存在能察觉的干涉现象［11］.1979年，Gensane最早进行了尝试，提出了一种能考虑不同反射波之间声压干涉叠加的虚源法［12］；Dance等［11］与Wang等［13］在1994年和2002年基于该理论分别研究了用于厂房空间和开放式办公室内声压场的相干虚源法预测模型.1989年，Lemire等［14］对点声源在闭空间内的声传播进行了研究，认为点声源的每次界面声反射为球面波，在此基础上，提出了一种目前广泛使用的相干虚源模型.2010年，陈妍等［15］在相干虚源模型基础上对不同声学边界长空间内部声场的相干模型进行了研究.对声源经有限长屏障多路衍射或半开空间内多重反射组成的户外相干声场，至今还未见对其研究.目前用于实际计算户外噪声的主要是基于试验和半经验方法的工程算法，这主要是考虑其他理论算法相对复杂和费时，对一些复杂的因素如地貌环境、气象环境等理论计算繁琐且一般受约束于具体条件，而工程算法基于统计学的一些经验公式，计算效率高，因此基于试验和半经验方法的工程算法目前得到了广泛应用.其研究成果主要是给出了目前广泛采用的ISO 9613-2标准算法，该算法对点声源的户外传播给出了具体可操作的计算公式，因此较早就进行了软件产业应用.ISO9613-2标准中对预测点倍频带声压级计算如下［1，16］

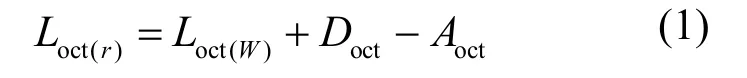
式中：Loct（r）为预测点等效倍频带声压级；Loct（W）为声源（包含虚声源）产生的倍频带声功率级；Doct为声源在倍频带上的指向性校正；Aoct为包含几何发散、屏障与大气吸收等引起的衰减之和.在目前的工程预测算法中点声源的相位信息没有得到反映，因此只能对声场的能量叠加，不能进行声场的相干叠加.

针对以上情况，本文基于几何衍射理论、相干虚源法等理论方法，结合工程算法的特点，建立一种考虑相位的户外噪声相干预测模型，该模型主要对衍射和反射两个主要户外声传播方式进行研究，要求在保证一定预测精度的情况下，能最大的提高计算速度，满足工程计算效率高的需求.

1 户外噪声相干预测模型

针对目前户外噪声预测算法中无法进行相干声源的辐射声场计算，且户外声传播中屏障和反射面又普遍存在的实际情形，本文从考虑工程算法特点角度出发，分别对户外噪声传播中的衍射声和反射声进行研究，提出一种考虑相位的户外噪声相干预测模型.

1.1 考虑相干的屏障衍射声工程算法研究

目前屏障的衍射声场理论严格解中，Hadden与Pierce基于几何衍射理论（GTD）得到的楔形屏障附近的严格解和试验结果吻合度很高，理论上无误差，而且可以解决声源或受声点距离屏障任何位置处的衍射计算，但因其理论公式复杂，一直未能用于工程噪声预测中.考虑户外噪声预测中，声屏障多按薄屏障进行处理，本节就其刚性楔形屏障中的薄屏障进行研究，基于Hadden-Pierce严格理论解推导出一种考虑相干的屏障衍射声简化算法，该方法可避免原始方法中复杂的数值计算和奇异积分的处理过程，能极大提高计算效率.

1.1.1 Hadden-Pierce严格理论解 图1为本理论中所用的刚性楔形体的声衍射传播几何图，采用圆柱体坐标体系（r，θ，z），其中刚性楔形边沿着z方向，其中两个楔形侧边所在的平面分别为θ=0 和θ=β，整个楔形变化角度为θ=0到θ=β（β＞π）.由图1可看出，因本文讨论的为薄屏障，对应的β=2π.

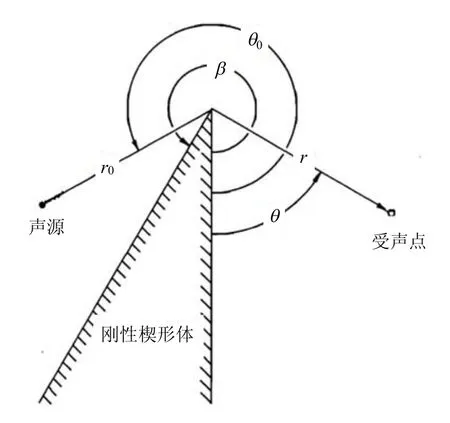
根据点声源经过楔形体时不同衍射路径，得到楔形体声影区中受声点的衍射声场方程，见下式［17］：

其中：

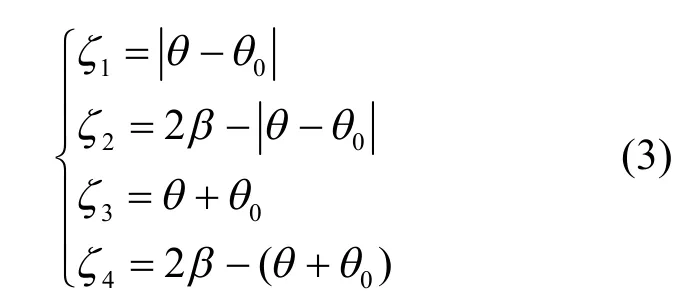
式（2）中：V（ζi）为经楔形体两个边界产生的衍射声，每项可表达为具体表达式：

其中A（ζi）为角函数，U（ζ）为单位阶跃函数，表示为

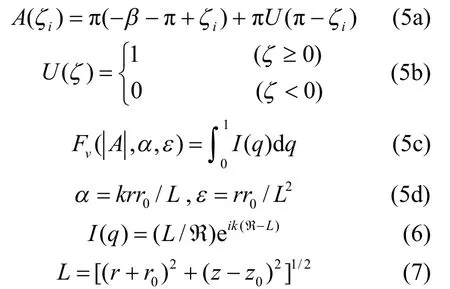
式中：α与ε为表达声源和受声点相对屏障位置的几何参数；r与r0分别表示受声点和声源到达屏障的距离；z和z0分别表示受声点和声源在z方向的坐标值；I（q）为积分函数；L定义为声源S经定边E1的衍射然后到达接受点R的总传播最短衍射距离；k为声源的波数；且i=，参数ℜ定义为边E1上衍射角为ζi的两点之间距离，如图2，可表示为

式中：Y为积分中间过渡变量：

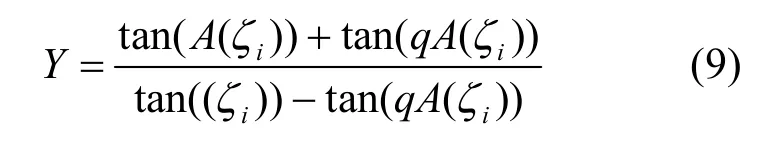
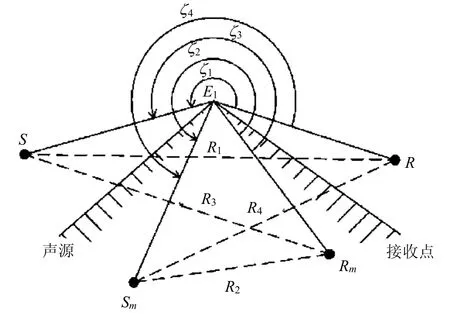
图2 参数R与ζi的几何描述Fig.2 Geometric description of parametersℜiand ζi

1.1.2 衍射声场通用工程简化算法 上节中给出了点声源在经刚性楔形体衍射后，屏障附近任意受声点的声场表达式，尤其是给出了衍射项V（ζ）理论解，但由于理论解中含有积分项，不适合工程计算用.本文针对声源和受声点最常见的几何位置，对位置几何参数α进行假设，最后通过积分变量的转化与分部积分对Hadden-Pierce严格理论解进行适合工程算法的简化，并根据有限差分法给出了涉及的Fresnel函数近似统一表达式，从而给出了本文计算薄屏障衍射声场的通用工程简化算法.

式（5c）中积分上下限为有限值，q值变化范围在0和1之间，但在求解时仅在kL≥1时为有限值，因此积分时存在数值波动大的情况，给计算带来困难.为改变积分上下限，使其不受限制，将式（5c）积分变量简单化，有利于数值求解.这里引入参数y代入变量ℜ，具体表达式为：

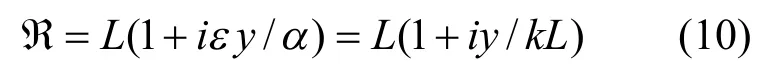
根据式（7）和式（8），可得：

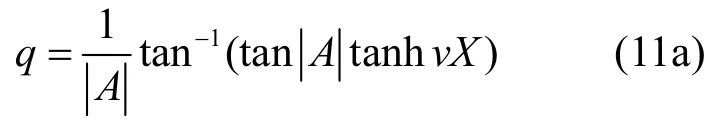
这里X为：

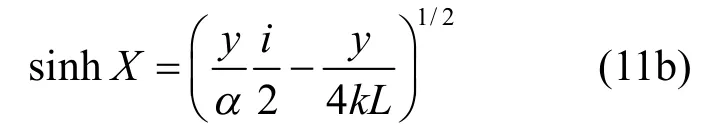
将式（10）中ℜ代入式（6），可以很容易实现变量从q转化为y，因此可转化成一个简便的表达式Fv，

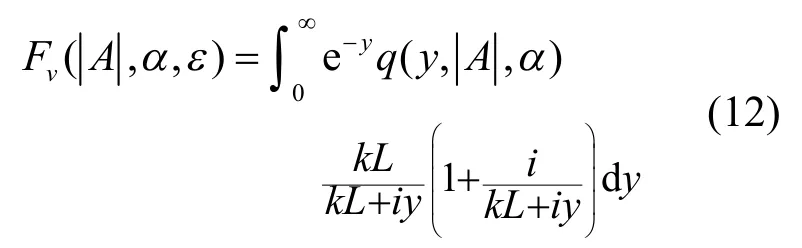
式（12）中由于几何参数都得以体现，积分变量明确，无需过多中间环节，易于数值求解.

式（5d）中参数α因包含了声源频率，声源和受声点与屏障之间距离，可作为重要几何位置参数变量.为得到通用的简化公式，这里假设α较大，即声源和受声点离屏障不是足够近时；而角函数|A|可取任意值，即受声点可取声影区边界附近或其他位置，事实上这种情况也为较为普遍.基于以上假设，很容易对式（12）进行简化，根据kL=α/ε，进行分部积分，从而消除积分项，其中因子dq/dy可由式（11）得到.为避免|A|=π/2时存在求值困难，假设y=u2，可得到积分值为某个固定倍数关系的表达项为：

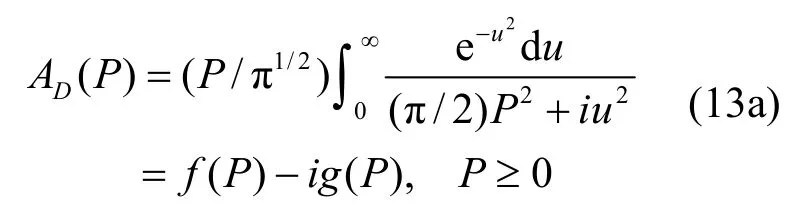
其中

这里f（ P）与g（ P）为辅助Fresnel函数，本文根据有限差分法给出了Fresnel函数近似的统一表达式为：

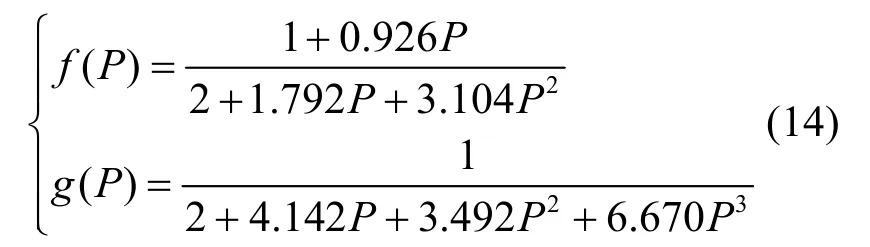
经以上计算，可得到Fv表达式为

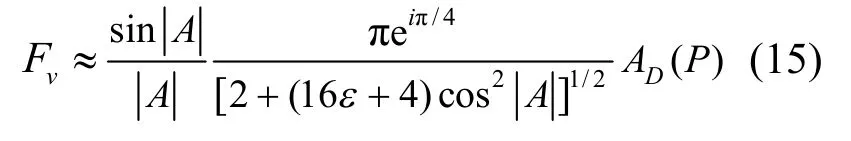
考虑相位的屏障衍射工程算法经整理如下：

1.2 多重反射声相干虚源法研究

除了屏障衍射声外，在工业企业中多重反射主要主要发生在由地面、两个有限长垂直屏障组成的半开空间内，其中各边界为声反射面或声吸声面.在前述研究反射声场的方法中，由于Lemire提出的相干虚源模型的适应性广，对研究声场的封闭并无严格要求，本文在其研究基础上，结合前节给出的衍射工程算法，提出一种半开空间声场相干虚源预测模型.该模型能考虑每次反射时界面阻抗对反射波相位的影响和总场中不同声波间的干涉影响，且通过得到反射面的每次实际正入射角而计算出来的反射系数更符合实际声传播，特别适合预测半开空间外较远距离的声传播.

如图3所示，侧面1和侧面2代表两侧屏障.W为两个侧面之间距离，H为侧面1和侧面2的高度.R和E1R、E2R分别表示受声点和左右两个侧面上方绕射点.侧面1、侧面2、地面的归一化导纳为βi（i=1，2，3）.

图3 虚源构造示意Fig.3 Schematic of image source construction

根据虚声源产生原理，当受声点在半开空间外部右侧时，左侧虚声源（m≤0）起作用，此时声线在两个屏障之间多次反射后，经过E2R衍射到达受声点R.反之，当受声点在半开空间外部左侧时，声线最后经过E1R衍射到达受声点R.另外，本文半开空间地面为具有一定反射系数的平面，因此在EiR（i=1，2）点的绕射声经地面反射后到达受声点R，这里给出了虚受声点R′.

半开空间的整个声场是由声源和所有虚源共同决定的，虚源是由声源在各反射面的不停反射生成的，无穷多次的反射产生了无穷多个虚源，于是，总声场可看成是由所有虚源的影响综合决定的，可得受声点的总声压为：

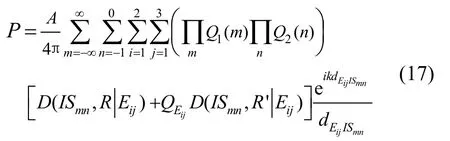
式中：A为点声源的源强系数；k为声源的波数；m、n（ m∈（-∞，∞），n ∈［-1，0］分别为x、z方向虚声源的位置参数；ISmn表示激励声源或虚源（后面统一简称虚源）；IS00特指声源本身；i（ i∈［1，2］）表示侧面1或侧面2；j（ j∈［1，3］）表示各侧面（有限长屏障）3条衍射边；dEij IS mn是虚声源ISmn到衍射边Eij的距离；QISmn为复数形式；是用于计算声波从ISmn到达受声点之间经过的所有反射界面的总声反射系数；QEij为声线经Eij边绕射后到达地面的反射系数；dEij IS mn为虚源ISmn到侧面衍射边上EijR点的距离；D（ ISmn）为虚声源经衍射边Eij到受声点R的单衍射系数；D（ ISmn，R）为虚声源经衍射边Ei到虚受声点R'的单衍射系数，单衍射系数计算公式为［18］：

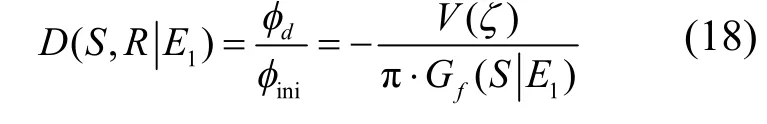
式中：E1表示衍射边；φini与φd表示传输到该边位置的初始声场和接受点处的衍射声场；Gf（S E1）表示三维空间中两位置S和E1的间的自由场格林函数，即为E1处的直达声；V（ζ）可采用前节计算屏障衍射声场计算公式，见式（16）.

Q1（ m）表示所经过的侧面的复数声波系数，Q2（ n）表示所经过的地面的复数声波反射系数.对于反射面的单次反射系数Qi，Lemire认为可以使用一个无限大界面上球面波反射场的近似解来求取，即［19］：

式中：Rpi为第i个反射面上的平面波反射系数.

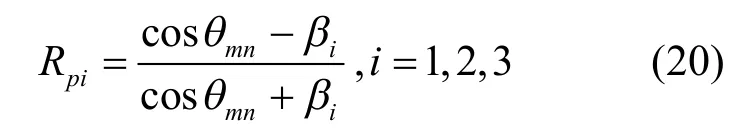
式中：θmn表示从虚源ISmn到受声点的声波传输路径在该反射面上的正入射角；iβ表示第i个界面的法向比声纳.式（19）中F（ w）为界面损耗系数，可表示为［20-21］：

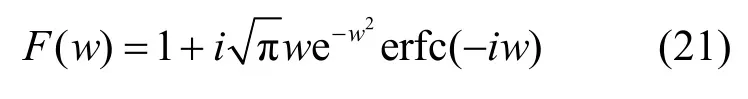
式中：erfc为余补误差函数；w是数值距离参数，与虚源的阶数m、n，入射角θmn以及相应的边界有关，定义为：

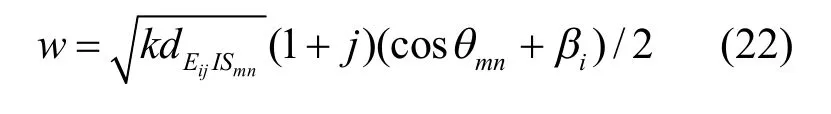
2 应用实例与分析

为验证本文提出的户外噪声相干预测模型的计算效率和准确性，以处于半开空间内某一电力变压器组为例，计算其周围的相干声场.

前文给出了点声源在半开空间内激发的声场预测公式，实际计算电力变压器组户外辐射噪声前，须将单个变压器表面划分成若干个单元，每个单元相当于一个点声源.电力变压器组布局图见图4.

图4 电力变压器组布局Fig.4 Layout of power transformer group

对于如图4所示的电力变压器组，现场多为不同相的变压器集中布置，一般为A相、B相、C相间隔分布，对于其中的单个变压器，根据现场测试和缩尺比例模型试验得到其表面单元点声源相位随机分布的特点，各划分点声源按不相干声源进行计算；而对于不同相的变压器，各相邻变压器之间电压由于存在一定的相位差120°，噪声又由于电压信号（激励信号）经过该线性系统的固定传递函数产生，因此对于某个确定的分析频率，则可认为在各个相邻变压器相同位置处的噪声（响应信号）相位差亦为120°，即等效点声源相位相差120°，需按相干声源进行计算.

2.1 变压器组户外噪声计算模型

根据本文提出的相干虚源模型建立变压器组户外噪声计算模型.该模型由3个变压器组成，按照A相、B相、C相间隔分布，反射面由4个平行的防火墙与刚性地面组成.各个变压器尺寸相同，其本体高度为4.6m，宽为4.0m，长为8.9m，防火墙高度为6.8m，长为15m，防火墙之间距离为7.5m.电力变压器中的防火墙与地面均为刚性反射面.考虑变压器模型区域对称性，计算场点网格区域大小设置为100m×100m，网格间距为2m×2m，高度设为1.5m，覆盖模型区域的1/4.为与各方法的模型计算结果对比，在计算场点网格的45°对角方向距电力变压器组中心由近至远设置了25个测点，每个测点高度为1.5m，各测点横坐标间距为2m.电力变压器组尺寸与现场测点分布图如图5所示.

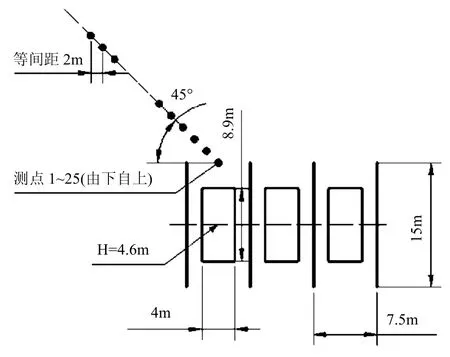
图5 电力变压器组尺寸与测点分布Fig.5 The size of power transformer group and distribution of measurment points

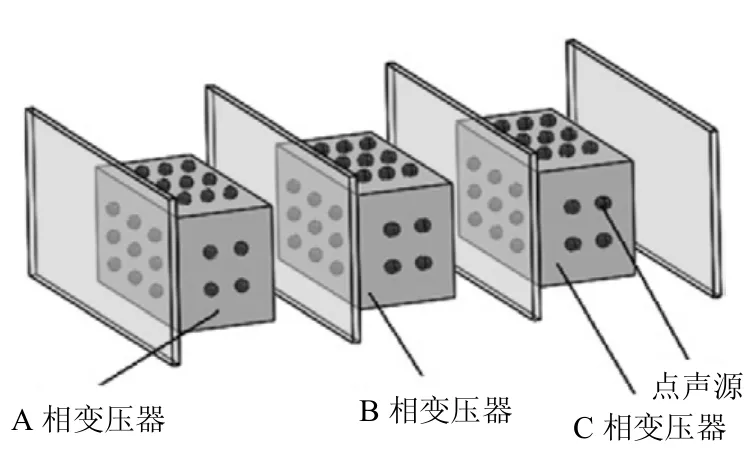
图6 电力变压器组点声源分布Fig.6 Point source distribution around power transformer group

根据声源的相位分布特点，将各个变压器分别离散成35个均匀分布的点声源，各个变压器声源的总声功率设为95dBA，根据电力变压器现场噪声频谱中优势频率为100Hz，选择点声源的计算频率亦为100Hz，实际上，本文的声学模型同样适用于类似变压器组中存在其他不同优势频率时的噪声计算.电力变压器各表面单元划分的点声源分布与几何尺寸见图6.现场噪声测试图片如图7所示，测试区域选择为电力变压器组相对集中的区域，附近无其他明显噪声源影响.

图7 电力变压器组组区域现场噪声测试图片Fig.7 The scene when measuring noise in the area of power transformer group

2.2 结果与讨论

分别利用边界元算法、基于ISO9613的Cadna/A预测软件和本文提出的户外噪声相干预测模型进行噪声网格地图的绘制，结果如图8～图10所示.

图8 基于边界元计算的噪声网格分布Fig.8 Noise distribution grid based on the boundary element method

由图8～图10可知，边界元法与本算法因为考虑了相位，反应了相干声场的波动性，可以看出有明显的干涉条纹，而利用ISO9613标准的Cadna/A预测软件则无明显的干涉条纹，是因为其算法中没有考虑相干影响，只是能量的叠加.同时对比边界元法和本算法绘制的噪声地图，声压级对应的颜色分布趋势相同，吻合度较高.而在计算时间上，应用本文提出的户外噪声相干预测模型耗时36.8min，而边界元法耗时160h，可见本算法的计算时间大大缩短.

利用本文噪声相干预测模型、边界元法、基于ISO9613标准的Cadna/A预测软件对场点网格的对角方向的25个测点进行计算，并将其计算结果与实测值进行对比，结果如图11所示.这里值得注意的是实测的声压级为所有频率段的噪声值累加，因本文考察的是100Hz，因此要根据其1/3倍频程频谱提取出100Hz对应的声压级.

图9 基于ISO9613的噪声网格分布（Cadna/A）Fig.9 Noise distribution grid based on the ISO9613（Cadna/A）

图10 本计算模型的噪声网格分布Fig.10 Noise distribution grid based on the proposed model

由图11可知，相比边界元法及实测的噪声值，本相干预测模型计算测点的噪声值误差均较小，除了个别点达到3dB，其他各点误差均在2dB以内，尤其当测点处于远场时，其声压级误差更小.ISO9613标准计算的声压级值能反映随着测点不断远离声源，其声压级不断降低的趋势.当测点距离声源较近时，ISO9613标准计算结果平均值要低于其他方法计算的声压值，考虑为相干虚源的叠加效果明显所致；而当测点距离声源较远时，ISO9613标准计算相比其它两种计算方法结果又偏大，造成这种原因是该算法中的镜像虚源法未考虑多次反射时，声线与边界面入射角度的变化引起反射损失逐渐增大的实际情形，造成ISO9613计算值偏高，而本文提出的计算模型误差较小，更适合较远距离户外声场的计算.

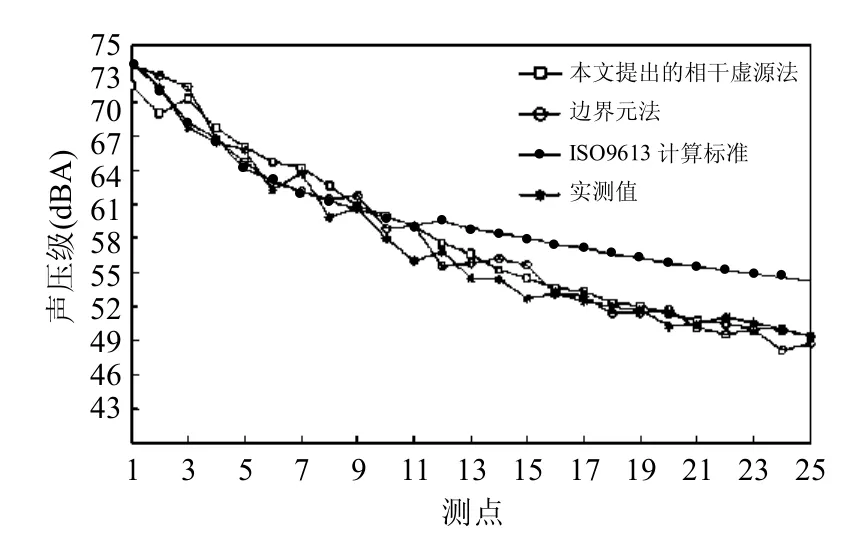
图11 三种方法计算测点的声压值与实测值的对比Fig.11 Comparisons between the directly measured sound pressure values and that calculated by the proposed model，by the boundary element method，and by the ISO 9613.

4 结语

基于几何衍射理论、相干虚源法等理论方法，提出一种适合于工程算法的户外噪声相干预测模型.该相干预测模型中提出的薄屏障衍射简化工程算法基于Hadden-Pierce严格理论解，为声场波动理论下的解析解，具有较高的计算精度；而提出的多重反射下的户外相干虚源模型不仅能考虑到刚性或吸声反射边界，而且能考虑多次反射后由于入射角的改变导致平面波反射系数的变化影响，更符合实际声传播.因此该相干预测模型不仅理论上能准确计算声源在经过有限长声屏障或多重声屏障时，由于多条路径衍射声形成的相干声场，还可理论计算声源在屏障等界面之间经多次反射后再衍射，或多个反射声形成的相干声场.

应用本文提出的户外噪声相干预测模型对某变电站电力变压器周围的相干声场进行预测，结果表明，该户外噪声相干预测模型能反映出声波在不同位置处的波动性，比原有的ISO9613模型更接近测试结果，证明了所提理论模型的有效性，可应用于大范围的户外相干噪声预测计算.

［1］ISO 9613-2： 1996，Acoustics- Attenuation of sound during propagation outdoors- Part 2： General method of calculation［S］.International Standards Organization，Genève，Switzerland，1996.

［2］Kuttruff H.Room acoustics［M］.Applied Science Publishers Limited，London，3rd edn，1991.

［3］Lacerda D L A，Wrobel L C，Mansur W J.A dual boundary element formulation for sound propagation around barriers over an impedance plane［J］.Journal of Sound and Vibration，1997，202（4）：235-247.

［4］Duhamel D.Efficient calculation of the three-dimensional sound pressure field around a noise barrier［J］.Journal of Sound and Vibration，1996，197（2）：547-571.

［5］LMS.Sysnoise user’s manual［R］.version 5.6LMS Numerical Technologies，2003.

［6］吴硕贤，赵越喆.建筑声学与环境声学［M］.北京：科学出版社，2003.

［7］Keller J B.Geometrical theory of diffraction［J］.Journal of the Optical Society of America，1962，52（2）：116-130.

［8］Bies D A，Hansen C H.Engineering noise control theory and practice［C］//E & FN SPON，London & New York，2nd ed，1996.

［9］Lindqvist E A.Sound attenuation in larger factory spaces［J］.Acustica，1982，50（2）：313-328.

［10］Dance S M，Shield B M.The complete image-source method for the prediction of sound distribution in non-diffuse enclosed spaces［J］.Journal of Sound and Vibration，1997，201（3）：473-489.

［11］Dance S M，Roberts J P，Shield B M.Computer prediction inserton loss due to a single barrier in a non-diffuse empty enclosed spaces［J］.J.Building Acoustics，1994（1）：125-136.

［12］Gensane M，Santon F.Prediction of sound fields inrooms of arbitrary shape： validity of the image sources method［J］.Journal of sound and Vibration，1979，63（5）：97-108.

［13］Wang C，Bradley J S.A mathematical model for a single screen barrier in open-plan offices［J］.Applied Applied Acoustics，2002，63（6）：849-866.

［14］Lemire G，Nicolas J.Aerial propagation of spherical sound waves in bounded spaces［J］.Journal of the Acounstical Society of America，1989，86（5）：1845-1853.

［15］陈 妍，刘嘉俊，邱小军.不同声学边界长空间内声场传播的相干模型［J］.南京大学学报（自然科学），2010，46（1）：26-33.

［16］李 楠，冯 涛，李贤徽，等.交通噪声地图的声源反演及修正计算［J］.中国环境科学，2013，33（6）：1081-1090.

［17］Pierce，A D.Diffraction of sound around corners and over wide barriers［J］.JASA，1974，55（5）：941-955.

［18］闵鹤群.开放式办公室内的声场预测方法研究［D］.南京：南京大学，2010.

［19］Attenborough K，Hayek S I，Lawther J M.Propagation of sound above a porous half space［J］.Journal of the Acoustical Society of America，1980，68（5）：1493-1501.

［20］Briquet M，Filippi P.Diffraction of a spherical wave by an absorbing plane［J］.J.Acoust.Soc.Am.，1977，61（2）：640-646.

［21］Embleton T F W.Tutorial on sound propagation outdoors［J］.J.Acoust.Soc.Am.，1996，100（4）：31-48.

Model for predicting outdoor coherent noise and its engineering application.

RUAN Xue-yun1，2*，WEI Hao-zheng2，LI Zhi-yuan2（1.School of Mechanical Engineering，Anhui University of Science and Technology，Huainan 232001，China；2.Institute of Sound and Vibration Research，HeFei University of Technology，Hefei 230009，China）.China Environmental Science，2015，35（6）：1877～1884

A model for predicting outdoor coherent noise based on the geometric diffraction theory and coherent image source method was presented.The proposed model was suitable to be used in the engineering algorithm.By using the proposed model，not only the coherent sound field formed by multiple paths diffraction when sound waves gone through a finite length barrier or multiple barrier，but also that formed by multiple reflections between interfaces of barriers，could be calculated.The proposed model was experimentally used to predict the coherent sound field around a power transformer in a substation，and the results of the proposed model were respectively compared with that predicted by using the ISO9613-2，that calculated by using the boundary element method，and the directly measured values.The comparisons showed that the proposed model was valid and could be used for predicting outdoor noise in a wide range.Furthermore，the comparisons showed that the proposed model could reflect the fluctuations of sound waves at different locations，and could give predictions closer to the measured values than the ISO9613-2model.

coherent sound field；noise prediction model；acoustic diffraction；reflected sound；coherent image source method；engineering algorithm

X827

A

1000-6923（2015）06-1877-08

阮学云（1978-），男，安徽枞阳人，副教授，博士，主要从事机械系统动力学及低噪声设计研究.发表论文20余篇.

2014-11-20

国家“十一五”科技支撑计划（2006BAA02A21）

* 责任作者，副教授，ruanxueyun@163.com