大型风能发电机组叶片反求再设计

陶庆，孙文磊

(新疆大学机械工程学院，新疆乌鲁木齐 830047)

叶片是风力发电机中的关键部件之一，风力机叶片的成本占整机成本的20%～30%，叶片的外形设计和翼型选择等方面都是影响风机性能和产能效率最为核心的技术［1］。大型风能发电机组叶片反求再设计的流程是由叶片的反求测量、叶片的逆向重构、叶片反求再设计、叶片的反求设计分析等四部分组成［2］。由于风力发电机叶片要求精度较高，表面复杂，因此要对叶片进行多角度的测量，不同角度得到的数据要通过测量系统进行拼接整合［3］。根据测量的数据对叶片进行逆向重构和复杂叶片曲面的重新建模是反求设计的基础操作，这个步骤进行之后才可以进行误差分析［4］。CAD 模型重建是以获取的叶片点云数据为输入，以叶片的数字模型为输出，它决定叶片CAD 模型的优劣［5］。文中提出一种大型风能发电机组叶片反求再设计的原理和方法，通过对大型风能发电机组叶片反求测量、大型风能发电机组叶片逆向CAD 建模、大型风能发电机组叶片精度分析与尺寸还原等，对反求扫描叶片模型进行剖析，寻找几何特征，探索制约叶片形状的基本因素，确定叶片截面参数计算公式，利用所开发的叶片翼型自动生成系统，完成叶片的再设计。叶片反求再设计，特别是设计原理的反求，是对产品的再分析、再建模的过程，通过误差分析与对比，形成新的设计方法和产品，是已有设计的设计。

1 大型风能发电机组叶片反求设计

1.1 叶片反求测量

根据大型叶片的特点，采用非接触光学测量与照相测量混合系统和测量方法，对大型风能发电机组叶片进行反求测量。相较于其他的测量方法，对于大型叶片的三维测量，作者研究的方法集合了高清摄影技术和光栅扫描仪两种测量方法的优点，具有较高的精度，较高的效率［6］。风能发电机的叶片是大尺寸复杂零件，含有大量的曲面结构，利用一张曲面来测量并获得需要的数据点是不现实的［7］。文中将叶片进行分区分片然后分别拟合不同的曲面片，最后再将片段进行拼合。叶片测量区域的具体划分如图1 所示。

图1 分段测量法

因为叶片属于大型零件，在进行扫描的时候，要多次扫描采集数据。在实际测量的时候，要将扫描仪沿风力发电机叶片的最长尺寸方向渐渐移动扫描，如图2 所示。

图2 大尺寸叶片测量

1.2 叶片逆向CAD 建模

在对两幅照片所采集的数据点进行拼合的时候，坐标的对齐是指每幅图片中包含所有点云的重新定位。而视图拼合指要将点云和坐标系对齐。对测量数据进行模型建立和对坐标系进行建模后，需要将其坐标统一，然后进行不同图像间的拼接［8］，拼接后的叶片点云图见图3。

图3 叶片点云数据

对于获得的叶片截面点云数据，进行截面点云的光滑和排序，再用合适的参数进行插值，拟合出对应的截面曲线。能用来进行叶片曲面建模的是上述得到的精度和光顺度都较高的曲线，得到的叶片特征曲线如图4 所示。

图4 获取截面特征曲线

在确定了截面特征曲线后，在截面上每条特征曲线的端点采用3DB 样条插值法获得边界曲线［9］。但是需要拟合的边界光顺度满足要求，这样就需要对曲面进行一些优化处理以满足精度要求。文中采用的方法对于曲率法矢量变化极小的特征边界也可以高效地实现提取。通过获取的截面特征曲线，在满足精度的要求下进行扫掠，即可形成叶片的实体CAD 模型，如图5 所示。

图5 叶片CAD 模型

1.3 叶片精度分析与尺寸还原

叶片尺寸还原是叶片原始设计参数的还原，设计参数的还原就是确定叶片的翼型也就是确定每个截面的叶片的三维坐标值及外形数据。应用文中开发的系统的创建截面功能按设计要求确定翼型之间距离，按距离提取叶片截面三维坐标值和外形数据。图6 给出了还原叶片的坐标及外形几何尺寸数据。

图6 叶片数据还原

2 大型风能发电机组叶片翼型分析

叶片再设计是对叶片再分析、再建模的过程，是已有设计的设计。通过分析叶片翼型可以发现，叶片沿垂直叶展方向上的截面的形状(或称翼型) 是相似的，不同半径下其翼型的主要区别就在于各截面上的翼型大小不同、翼型在不同截面沿着某一点旋转了不同的角度以及厚弦比不同，需要确定r (叶片长度)、弦长cr(翼型大小)、β (旋转角度)、t (厚弦比) 这些值，便可以设计出任何形状的叶片。

叶片再设计的难点在于如何将不同r 下对应的翼型精确地绘制出来，所要解决的问题是要确定翼型数据在r 下所对应的坐标值发生怎样的变化。从对叶片几何参数所研究的结果看，影响翼型数据点的因素主要是弦长cr、扭角β 以及厚弦比t，如图7 所示。

图7 叶片结构外形影响因素

下面通过计算和推导探讨cr(弦长)、β (扭角)以及t (厚弦比) 和翼型的关系。

假设所要设计翼型上的一个点为i，i 距离旋转中心的距离为r。i 在X、Y、Z 轴上的坐标分别为Xi、Yi、Zi。在点i 处，弦长、扭角、厚弦比分别为cr、β、t。X0、Y0、0 分别是此点在单位翼型数据库中对应的数据。那么：

(1) 弦长cr与翼型数据值的关系

Xi、Yi、Zi在X、Y、Z 轴上的坐标与翼型数据库中对应点之间的关系为：

由对应关系可以得到翼型的变化，情况如图8 所示。

图8 弦长对翼型数据的影响

(2) 扭角β 与翼型数据值的关系

翼型的旋转变化并不像图9 (a) 那样绕着坐标零点旋转，其旋转的方式是如同图9 (b) 所示，旋转中心到叶片顶端的距离与整个叶片长度成一定比例，此比例根据不同的翼型有所区别，一般在弦长的1/4 处，这样可以有效地降低叶片受到空气作用所产生的扭矩。

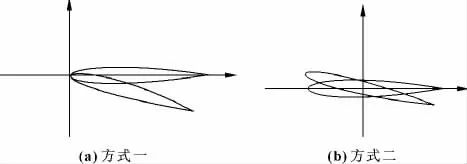
图9 翼型旋转的方式

综上所述，有两种方法可以处理在计算过程中旋转翼型的情况：按图9 (a) 计算和按图9 (b) 计算。后一种方法虽然直接，但由于单位翼型数据并不是以旋转点为旋转中心，另外，此方法牵涉到4 个象限的计算，程序计算较为复杂，所以，旋转计算通常都是采用先将数据点沿零件旋转然后再平移的方法。具体的计算方法为：

其中：τ 为旋转中心到顶端的距离/弦长cr，由此得到的翼型变化情况如图10 所示。

图10 扭角对翼型数据的影响

(3) 厚弦比增长率t 与翼型数据值的关系

厚弦比的改变主要是使翼型在垂直弦长方向的变化，也就是翼型数据点的Y 坐标要相应地乘上一个比例，即厚弦比增长率t。但是一定要在旋转变化之前先将厚弦比的变化进行计算好，不然变化的过程就会附加坐标的变化在其中，使翼型发生畸变，如图11 所示。

图11 厚弦比对翼型数据的影响

3 大型风能发电机组再设计叶片性能分析及验证

将反求设计得到的功率为750 kW 的风能发电机叶片的设计模型和实物相比较，利用GHBladed 对叶片的功能参数等进行进一步的分析验证，比较反求设计的叶片的精确度与正确度。

3.1 叶片对比条件

利用GH 来模拟湍流风的风速平均为14 m/s，横向和径向湍流强度分别为13.35%、17.08%。垂直湍流强度为9.45%，生成轮毂处的湍流风如图12 所示。

图12 轮毂处湍流风速

把反求扫描实际叶形、理论叶形和再设计修正叶形这3 种翼型数据输入到GH Bladed 中，可得到3 种相应的叶形，如图13 所示。

图13 GH Bladed 叶片模型

3.2 叶片对应的性能及表现

下面是一组针对750 kW 实际叶片扫描模型、理论计算模型和再设计修正模型的叶片参数对比分析，主要表现叶片弦长和扭角走势及对比分析，如图14、15 所示。

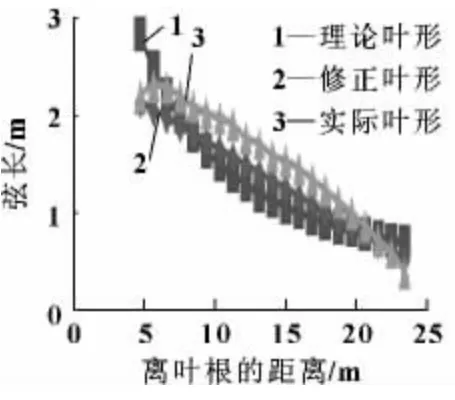
图14 弦长走势

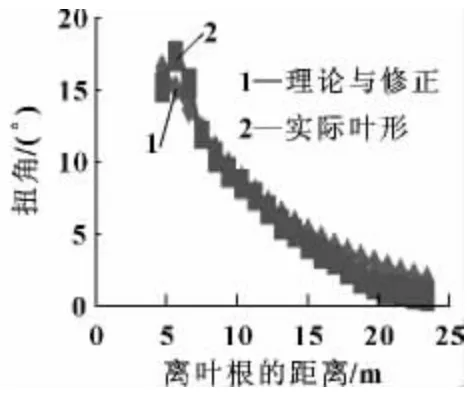
图15 扭角走势

从图中可以看出：理论模型的弦长要比修正和实际模型的弦长都要小，修正后的弦长比实际模型要小。这说明在实际叶片设计中弦长增大较大。实际的750 kW 叶片弦长近似接近直线，与修正后的叶形比较接近，并且在叶根处减少了较多的材料，修正后的叶形质量将比其他两种都要轻。理论模型与修正模型的扭角变化趋势相同，而比实际叶形增长速度缓慢，即前端扭角较小、根部扭角基本相符，说明实际叶片设计中为了较多地利用叶片前端产生力矩，减小了叶片前端的扭角。

3.3 叶片对比结论

(1) 实际叶形能够产生的电能较设计修正叶形大，设计修正叶形较理论叶形产出电能大，理论叶形接近设计功率临界位置，与设计目的相符;

(2) 在达到设计功率要求的前提下，低风速下设计修正叶形与实际叶形的各种载荷表现非常接近，风速升高时，设计修正叶形性能低于实际叶形，而理论叶形与修正叶形表现很接近;

(3) 沿叶展方向上看，设计修正叶片各种性能都围绕实际叶片变化，但有一定波动值，不如实际叶片的变化较为平稳，主要可能是各截面翼型旋转轴线的选择上需要进一步优化。

通过上面的分析，叶片再设计结果基本达到设计要求，与实际扫描叶片在气动载荷综合性能上相差较小。

4 结束语

通过对大型风能发电机组叶片反求再设计研究，对叶片反求测量扫描、叶片逆向CAD 建模、尺寸还原与精度分析，针对反求叶片模型进行剖析，寻找几何特征，在确定叶片截面参数计算公式及现有扫描点云数据重构的三维叶片模型特点后，提出一种大型风能发电机组叶片反求再设计的原理和方法，开发了一种可以通过输入和控制参数自动生成叶片翼型的系统，完成了叶片再设计。设计结果表明达到了设计要求。

［1］HERBERT G M J，INIYAN S，SREEVALSAN E，et al.A Review of Wind Energy Technologies［J］.Renewable ＆Sustainable Energy Reviews，2007，11(6) ：1117 -1145.

［2］WOODS Teresa J，VIGNOLA Joseph F，JUDGE John A.Surface-normal Vector Velocity Measurement Using a Fiveaxis Contour Scanning Laser Vibrometry System［J］.The International Society for Optical Engineering，2007，4(7) ：12 -17.

［3］WENLEI S，QING T，KANG J，et al.Establishing Largescale Wind Turbine Blade CAD Model Based on Reverse Engineering［C］//Proceedings of the 19th International Conference on Automation and Computing：Future Energy and Automation，2013：208 -211.

［4］汪俊，周来水，安鲁陵.具有复杂轮廓特征的实体模型重建方法［J］.中国机械工程，2006，17(11) ：1157 -1161.

［5］程晓亮.基于双目立体视觉的三维重构研究［D］.哈尔滨：哈尔滨工业大学，2006.

［6］张卡，张道俊，盛业华，等.三维坐标转换的两种方法及其比较研究［J］.数学的实践与认识，2008，38(23) ：121-128.

［7］吴晓峰，张国雄.现代大尺寸空间测量方法［J］.新视点，2006(10) ：68 -70.

［8］曾怀恩，黄声享.三维坐标转换参数求解的一种直接搜索法［J］.武汉大学学报：信息科学版，2008，33(11) ：1118 -1121.

［9］柯映林，陈曦.基于局部特征匹配的对称面提取算法［J］.计算机辅助设计与图形学学报，2005，17(6) ：1191-1195.