感应电动机堵转时内角接单相投入冲击电流的解析计算和分析

吴 玲

（西安高压电器研究院有限责任公司，西安 710077）

三相感应电动机在工业中得到广泛的应用。从感应电动机的原理可知，电动机在工频、额定电压下直接起动瞬间，电动机的起动电流为额定工作电流的4～7倍，起动电流过大时，将使电动机受到过大的电磁力冲击；同时由于起动应力较大，使得负载设备的寿命降低[1]。随着电力电子器件的发展，一种以微处理器控制大功率晶闸管的软起动器得到应用[2]。

软起动的常规控制方法有两种，即 alpha控制和gamma控制，晶闸管内角接的控制方法结合这两种控制方法[3]。在本文中，基于晶闸管-感应电动机控制系统内角接软起动，采用坐标旋转的方式所建立起来的数学模型，推出单相导通定子电流的解析表达式。为研究最佳初始触发角，我们假设不考虑转速（即堵转情况下），可以精确的推导出电流的解析表达式，根据电流波形选择合适的初始触发角来控制首半波冲击电流的幅值，这种通过控制初始触发角的方法对软起动的控制方法有十分重要的指导意义[4]。

本文从感应电动机堵转内角接单相投入的运动方程出发，导出了定子电流的解析解，最后用Matlab程序仿真了一台2.2kW三相感应电动机，得到了不同时刻投入时定子电流的波形的数值解（定步长欧拉法），并和解析解得出的波形进行了比较，并且得到肯定的结果，在解析解的研究方向有大的突破，通过比较波形，误差在允许范围内。

1 晶闸管与感应电动机绕组内角接单相导通的数学模型

图1是将晶闸管直接与电动机绕组在角型连接内部串联起来的一种调压电路，称为内角接方式。

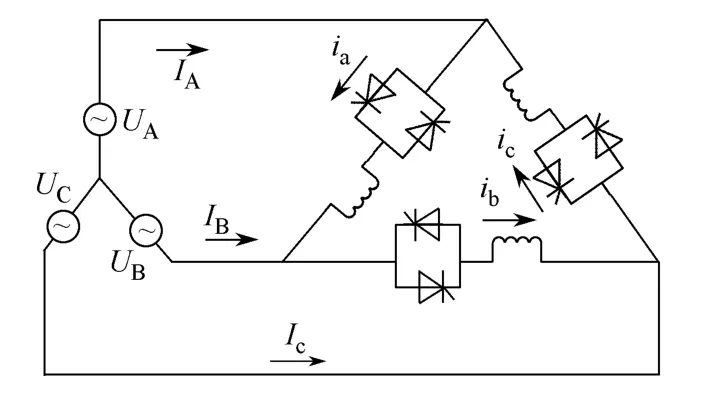
图1 晶闸管和电动机绕组内角接

电动机绕组的6个抽头接线全部引出，接线较为复杂，此电路由于控制器件在三角形连接内部，每一相晶闸管可以控制本身一相绕组，在研究时可以将其等效为单向调压电路研究，在控制和研究上比较简化，经过分析可以发现，其与晶闸管外接电路相比有调压角度范围大、线电流受到冲击小、谐波含量少、晶闸管承受电流小等优点[2]。

图1所示的内角接的连接方式，有4种导通方式：三相全部导通、两相导通（ab两相导通、bc两相导通、ca两相导通）、单相导通（a、b、c相分别导通）、三相全不导通。下面我们就单相导通来分析其数学模型。

为得到αβ0坐标系下的电动机模型，需要对三相电源进行如式（1）变换（式（1）中的x变量可以是电源电压变量、电流变量或磁链变量），将三相电压 (ua,ub,uc)变换为α、β坐标系下的两相变量(uα,uβ)[8]。

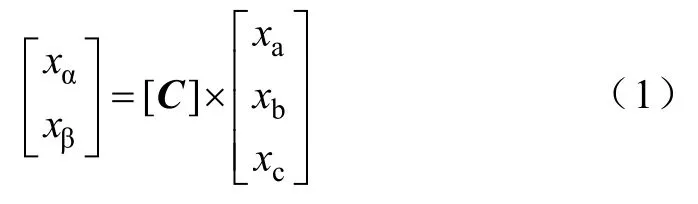
式中，当α轴与A相绕组轴线重合时，变换矩阵为

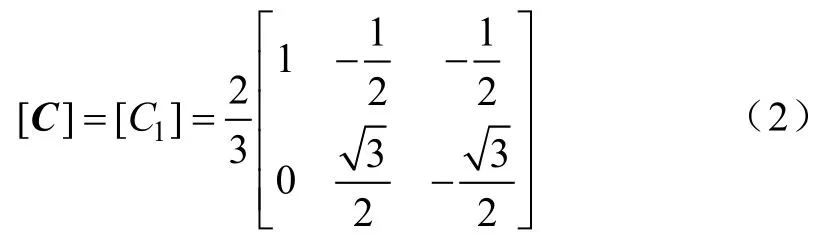
A相导通，BC相断开时，此时选α轴与A相绕组轴线重合。

当仅有一相晶闸管导通时，假设B相和C相晶闸管都不导通，B相绕组和C相绕组中均没有电流，即ib=ic= 0 ，取两相坐标的α轴与三相坐标的A相绕组轴线的电流ia重合，则有

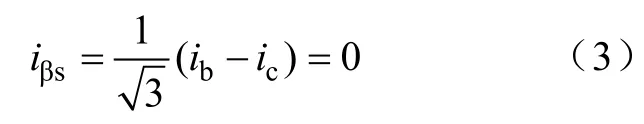
由式（3）和内角接矩阵方程（见附录）有

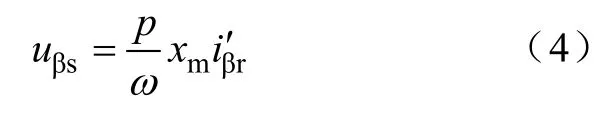
由于

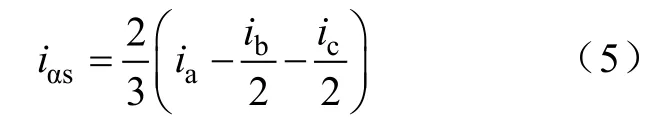
且有

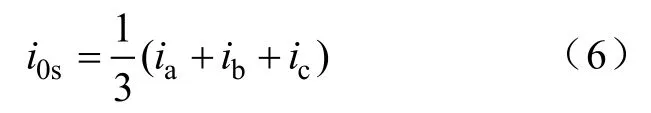
由于ib=ic= 0 ，代入式（3）和式（4）得

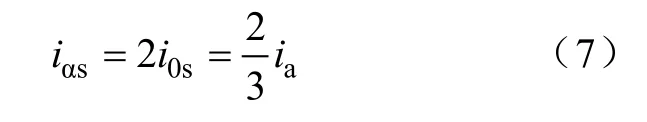
所以

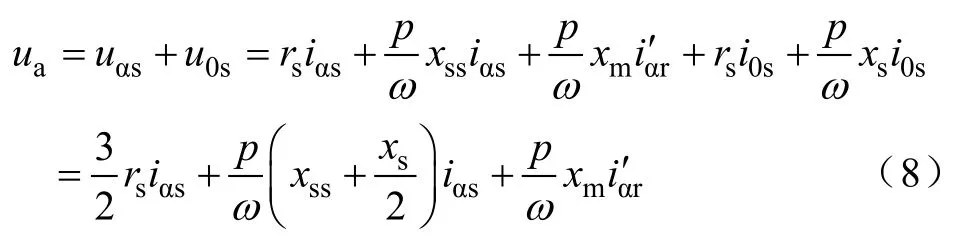
因此，对于仅有A相绕组导通的状态，系统电压方程为[2]

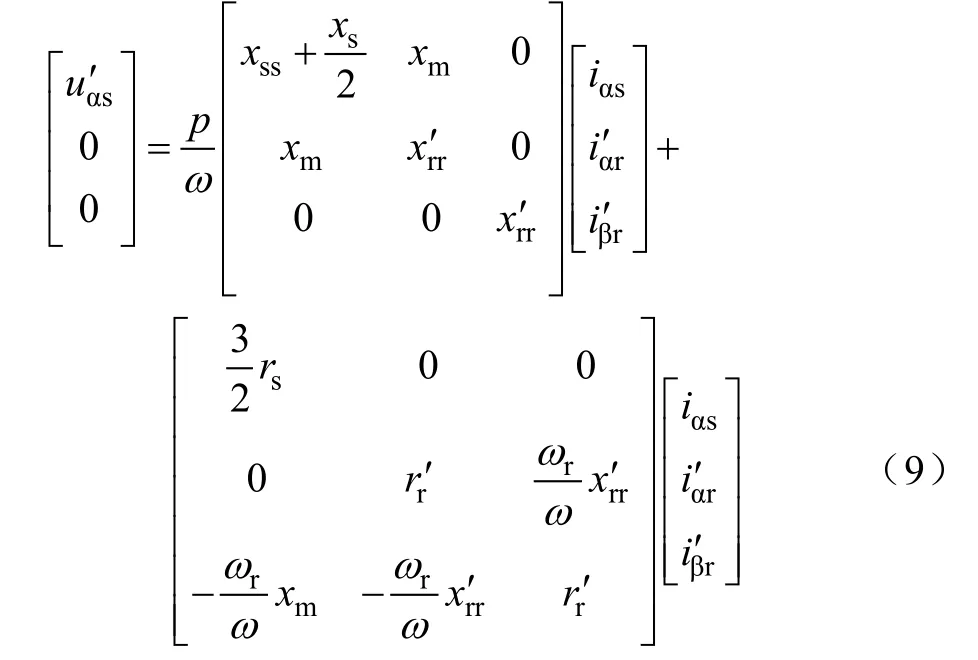
2 内角接单相导通的的解析解

对式（9）进行拉普拉斯变换[5]得

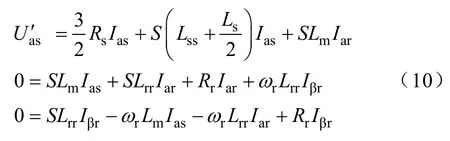
其中

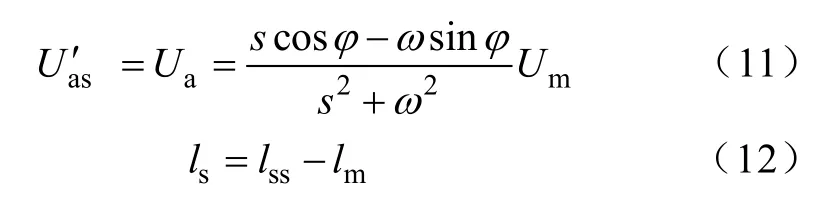
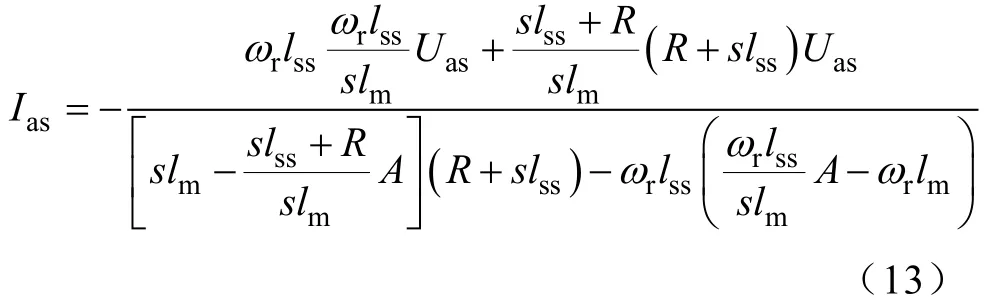
式（13）是A相单独导通定子电流的复频域的表达式，为分析方便，对其进行拉普拉斯反变换[3]。令

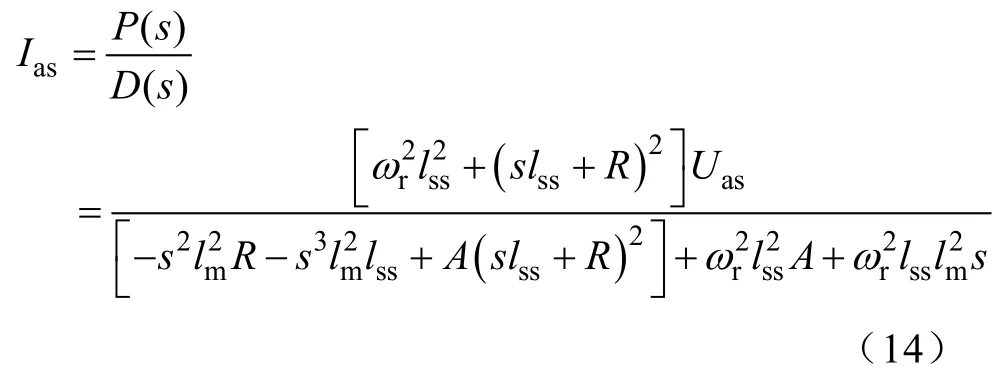
不考虑转速，即处于堵转状态时，ωr=0时，表达式（14）变成

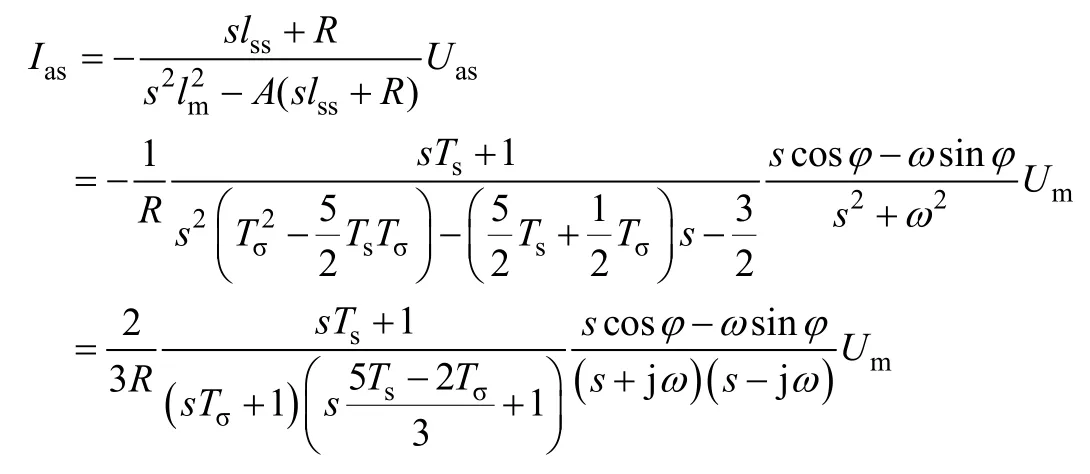
对其拉氏反变换所以有

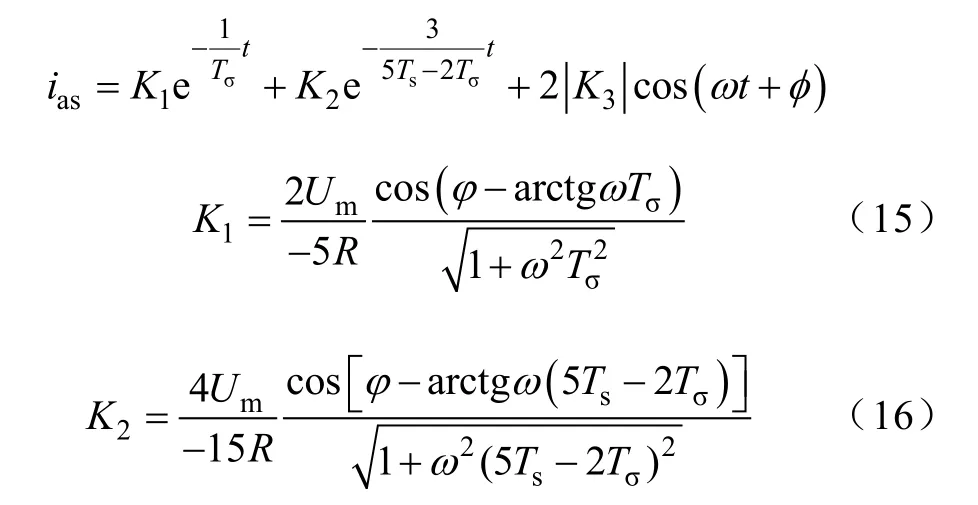
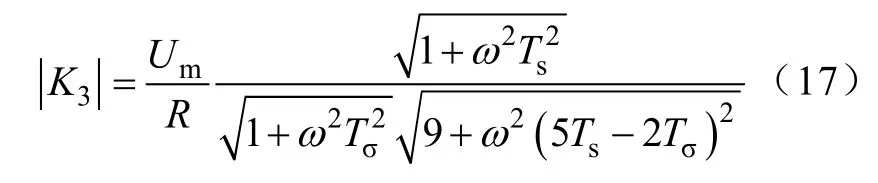
令t=0时，-K1-K2+ 2cosφ= 0，则有

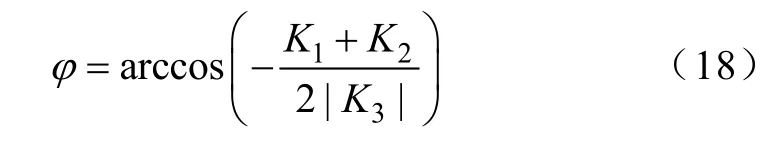
因此

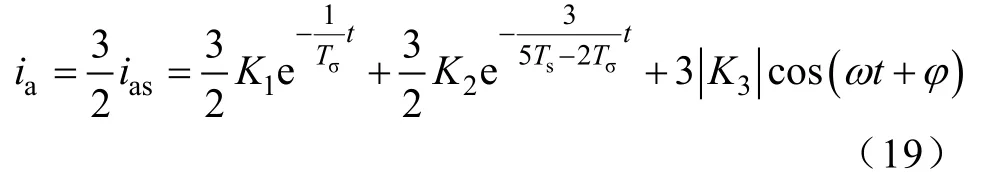
从式（19）可看出电流与参数的关系：由两个指数衰减分量和一个余弦分量组成，和参数Ts，Tσ，φ和K1、K2、K3有关，而K1、K2、K3都与电源最大幅值Um、电源的角频率ω、Ts，Tσ、R有关。

3 实例仿真

用一台2.2kW、50Hz、4极、380V的三相笼型感应电动机进行实例仿真，已知该电动机在工作状态下的参数为Rs=Rr= 6 .928Ω ；Lsσ=Lrσ= 0 .045H；Lm= 1 .55H；转动惯量J＝0.0235 k g·m2，摩擦阻力系数为0.00375(n·m ·s) /r ad 。代入式（15）～式（19）得

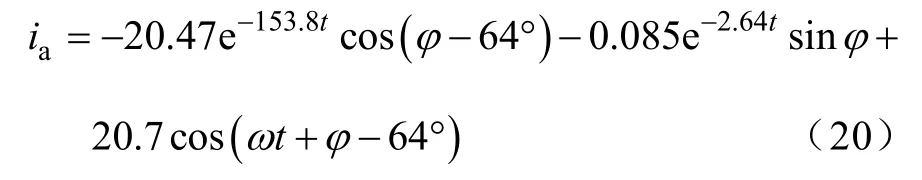
其中

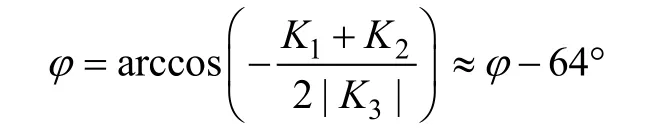
式（20）说明电流由两个直流衰减分量（一个是为保证漏磁通不突变对应的漏磁通的衰减分量，另一个是为保证主磁通不突变对应的衰减主分量）和一个正弦稳态分量。其中，第一个直流衰减分量对电流的影响起主要作用，直流衰减分量的初值与电源相位φ相关，可通过设置投入时φ角来减小冲击电流。

下面分别对φ=154°，φ=64°，φ=10°这三种情况分析电流aI的波形，仿真波形如图2至图4所示。

从图2至图4可看出，解析解和M语言解出的数值解相位完全一致，幅值有一点偏差，由于数值解用的是定步长的欧拉法，本身的算法会有所差异，但是这种误差是在允许范围内的，因此可以证明我们的这种解析解是正确的。

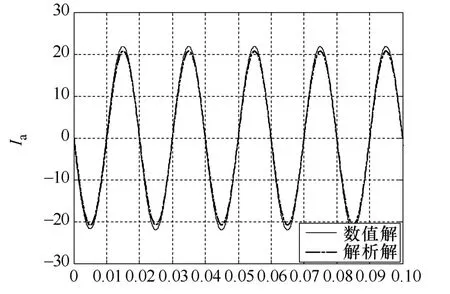
图2 φ=154°时Ia的数值解、解析解

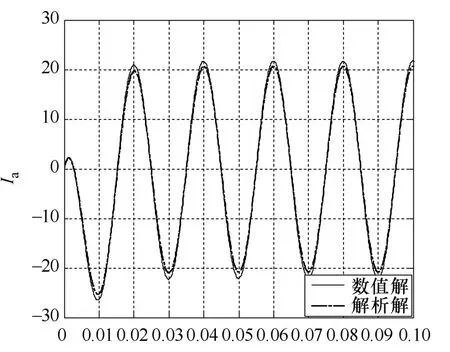
图3 φ=64°时Ia的数值解、解析解

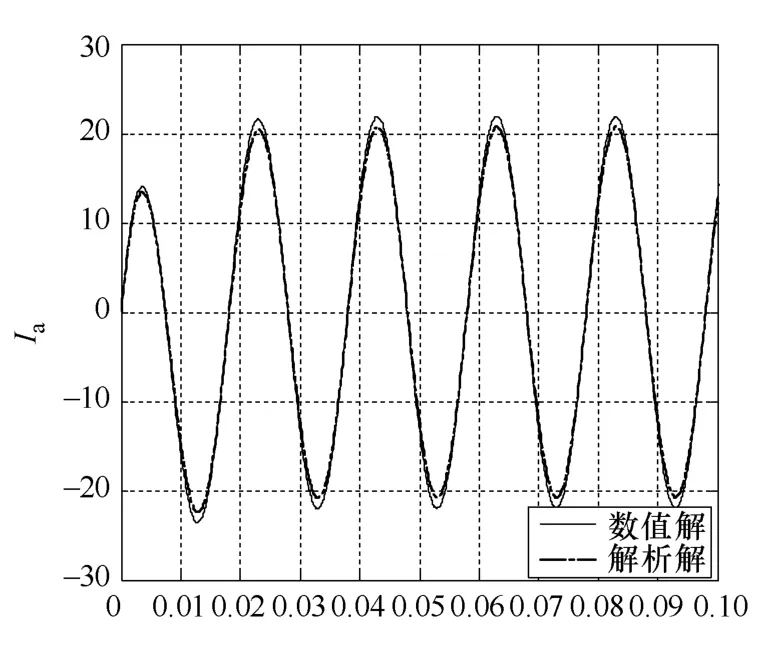
图4 φ=10°时Ia的数值解、解析解

当154φ=°时，第一个分量为零，电流最小，波形基本上是正弦波；当64φ=°时，首半波的电流比较小，但是又不能太小，在电动机还没启动就过零了就没起到软起动的作用；当10φ=°时，首半波的电流比稳态电流小，达到很好的控制首半波冲击电流的效果。因此我们通过控制每半个周期的导通角的就能达到限制电流冲击的目的。

4 内角接单相导通的的稳态解析解

t→∞时，当电流达到稳定，即

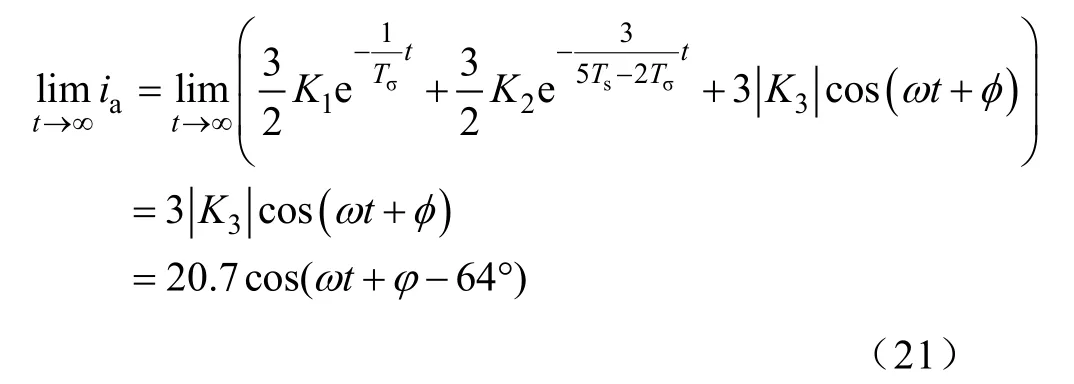
这时绕组单相导通状态与单相感应电动机的等效电路是相同的（加上零序）[2-11]，所以可以用单相等效电路来验证稳态解析解的正确性。内角接单相导通的稳态等效电路如图5所示。

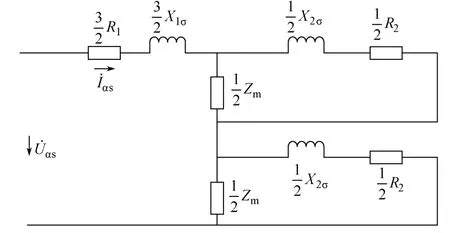
图5 内角接单相导通的稳态等效电路

通过分析得到单相等效电路稳态定子电流为

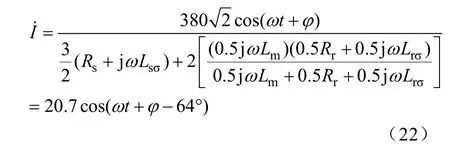
从上面两个表达式可以看出，当电流达到稳态时，电流的解析表达式是幅值为20.7，角频率为ω，初相角为64φ-°的余弦周期函数，与衰减时间常数没有关系。

5 结论

1）本文推导出内角接单相导通电流的表达式，两个直流衰减时间常数，漏磁通衰减时间常数对电流的衰减比较小，因此可以选择适当的初始触发角，衰减分量对电流的影响也会不同的。

2）通过对φ的选择，找到了合适的触发角，对软起动初始触发角的控制有指导意义。

[1] 高景德, 王祥珩, 李发海. 交流电机及其系统的分析[M]. 北京: 清华大学出版社, 1993.

[2] 徐广源. 感应电机在变负荷条件下软启动及跟踪控制研究[D]. 北京: 华北电力大学, 2007.

[3] Gritter D, Wang D, Habetler T G. Soft starter inside delta motor modeling and its control[C]//Industry Applications Conference, 2000. Conference Record of the 2000 IEEE, 2, 2000: 1137-1141 vol.2.

[4] Zenginobuz G, Cadirci I, Ermis M, et al. Soft starting of large induction motors at constant current with minimized starting torque pulsations[J]. Industry Applications, IEEE Transactions on, 2001, 37(5):1334-1347.

[5] 金忆丹. 拉普拉斯变换[M]. 杭州: 浙江大学出版社,2004.

[6] 邱关源. 电路[M]. 4版. 北京: 高等教育出版社,2006.

[7] 罗庆来, 宋柏生. 高等数学(下册) [M]. 北京: 高等教育出版社, 2003.

[8] 张锦豪, 邱维元. 复变函数[M]. 2版. 北京: 高等教育出版社, 2003.

[9] 汤蕴璆, 史乃. 电机学[M]. 北京: 机械工业出版社,1999.

[10] 张志涌. 精通 Matlab 6.5版[M]. 北京: 北京航空航天大学出版社, 2003.

[11] 李发海, 朱东起. 电机学[M]. 3版. 北京: 科学出版社, 2000.