包含外强迫因子的大气气溶胶数浓度的预测

陈潇潇，王革丽，金莲姬（1.中国科学院大气物理研究所，中层大气与全球环境探测开放实验室，北京10009；.南京信息工程大学，中国气象局气溶胶与云降水重点开放实验室，江苏 南京 10044；3.福建省平潭县气象局，福建 平潭 350400）

包含外强迫因子的大气气溶胶数浓度的预测

陈潇潇1，2，3，王革丽1*，金莲姬2（1.中国科学院大气物理研究所，中层大气与全球环境探测开放实验室，北京100029；2.南京信息工程大学，中国气象局气溶胶与云降水重点开放实验室，江苏 南京 210044；3.福建省平潭县气象局，福建 平潭 350400）

利用慢特征分析（Slow Feature Analysis， SFA）方法提取大气气溶胶时间序列的外强迫因子信息，并将此外强迫因子信息嵌入到预测模式中，建立一个包含提取外强迫因子信息的预测模式.利用该方法对2011年6月1日至2011年9月14日黄山山底的每小时大气气溶胶数浓度时间序列进行预测试验分析.结果表明，当提前预报一步时，平稳性模式的预测结果与实际观测数据的相关系数为0.6982，而单一外强迫模式的相关系数为0.7390，强迫模式的相关系数是0.7475，外强迫的加入可以有效的提高预测技巧.

慢特征分析方法；外强迫因子；大气气溶胶预测

就真实的天气系统来说，控制它的外部条件不是一成不变的，这种外部条件的随时间的变化，会使得大气系统平稳性质的改变，因此大气系统的动力学性质本质上是非平稳的［1-2］.在一些天气和气候过程中，人们发现了大气过程的平稳性被改变的事实.考虑到系统非平稳行为的根本原因在于外部强迫随时间的变化［3］.Wang等［4］发展了一个建立在外强迫基础上的预测模型，尝试在预测模式中引入人为设定的“理想”外强迫因子信息，试验结果表明该方法可以有效地提高预测精度.然而该方法的一个缺憾在于加入了人为设定的可能的外强迫因子.因此，本文考虑从时间序列中提取外强迫因子并建立包含外强迫因子时间序列的预测模型.这样一来，外强迫的提取就成了主要矛盾.目前外强迫因子的重构或者提取方法主要有两种，一是Verdes提出的“交叉预测方法”［5］，这个方法是根据局部线性映射来追踪外强迫的演变.另一个是Wiskott提出的“慢特征分析法”［6］，此方法可以从快速变化的信号中提取缓变特征，可以从时间序列中评估一个单一潜在的外强迫因子.这两种方法都被应用于一些非平稳时间序列的分析中并得到了较好的结果［7-8］.

在这些工作的基础上，本文尝试利用慢特征分析方法从时间序列提取外强迫因子，并将此外强迫因子信息嵌入到预测模式的建立中，建立一个包含提取的外强迫信息的预测模型.

旨在研究外强迫因子在预测中的作用，希望通过外强迫因子的加入有效的提高预测技巧.

1 与慢特征分析方法结合的非平稳时间序列预测建模技术

与慢特征分析方法结合的非平稳时间序列预测建模技术可以简单分为2个步骤，一是外强迫信息的提取，二是预测模型的建立.

1.1 外强迫信息的提取—慢特征分析方法

慢特性分析方法（Slow Feature Analysis，简称SFA），它的总体目标是从快速变化特征信号中提取慢变特征信号.基本思想是借助于重构的函数空间，在约束条件下，将时间序列信号展开投影到变化最慢的方向，这个投影方向的时间序列信号分量就是外强迫因子.

对于一个给定的I维时间序列的输入信号xt=［x1（t），…xI（t ）］T进行标准化，得到n阶方阵

其中〈〉t表示变量对时间求平均.以上的这种标准化也称为白化，矩阵S就是n×I维的白化矩阵.白化矩阵S可由主成分分析（PCA）方法得到，它的作用是让n阶方阵z（t）的协方差矩阵是一个单位矩阵，即并且白化过程减去了矩阵的平均值，所以可知

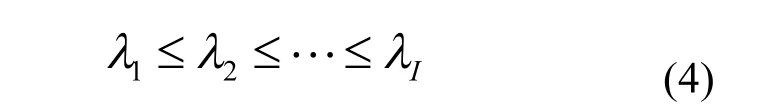
这时输入-输出函数变为

输出信号为

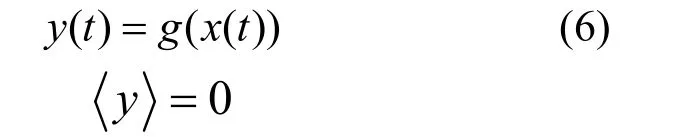
其中

输出信号满足零均值，并且单位方差是不相关即相互正交的.最慢的特征输出信号分量y1就是系统的外强迫因子.

本次实例数据来源于某河道的控制测量，每隔5 km左右布设一对D级GPS控制点，一共布设16点，每个控制点均联测四等水准高程。四等水准测量采用S05级电子水准仪和配套的铟瓦水准尺进行，并严格执行GB/T12898—2009《国家三、四等水准测量规范》。

1.2 预测模型的建立—状态空间动力学预报模型

重构状态空间理论有两个重要参数嵌入维数m和时滞参数τ.嵌入维数m是指重构空间的空间维数，选取嵌入维数m所遵循的规律是提供一个足够大的重构空间来展开嵌入的点集.时滞参数τ可以简单理解为“一个时间段”.当时滞参数t取值过小时，重构后的各个分量的相关性较高，将被嵌入到空间的主对角线上.而当时滞参数t取值过大时，重构后的各个分量几乎都不相关，使得重构的的空间显得很复杂，甚至扭曲了原始的动力系统.

状态空间动力学预报模型本质是寻求动力学相似，即利用历史上相似状态的演变来预报当前状态的演变.因此，可以在当前状态附近找出一个点域，这个点域中的相点按照轨线所指示的动力学演变到新的相点，综合结合这些邻近相点的信息，根据猜测或者已有的物理学上得知识，构造一个映射，并用它来预测当前点未来的演变［9-13］.

发展建立的与SFA方法结合的非平稳时间序列预测建模思路如下：

考虑包含2个时间序列｛xi ｝i=1，2，...，n和 ｛αi｝i=1，2，...，n的一个非线性非平稳过程，前者是系统的状态随时间的变化，而后者表示其外强迫随时间的演变.借助于一个适当的时滞参为数τ，我们可以将它们嵌入到m1+ m2维的状态空间中，并得到如下的状态轨线：

或者简写为：

其中m1和m2分别为｛xi｝及｛αi｝的嵌入维数，N=n－（max（m1， m2）－1）τ为轨线上的相点数目.｛xi｝表示动力系统的时间序列，在随后的预测试验中， ｛xi｝即为黄山山底的每小时大气气溶胶数浓度的时间序列.｛αi｝表示利用SFA方法从｛xi｝中提取的外强迫因子的时间序列.可建立如下的预测模型：

2 黄山大气气溶胶数浓度时间序列的预测分析

2.1 气溶胶观测资料

预测试验所用数据是利用美国MSP 公司生产的宽范围粒径谱仪（WPS）观测的黄山山底大气气溶胶数浓度数据［14］.观测地点为黄山山底（30°3' 31' ' N； 118°09' 56' 'E；海拔高度：485m），位于寨西自动气象站旁60m.

所用的大气气溶胶数浓度的粒径范围是0.1～10μm.大气气溶胶数浓度资料的观测时间是2011年6月1日至2011年9月14日每小时的气溶胶数浓度值，预测试验中总时间序列的资料长度是2234h.

2.2 大气气溶胶数浓度时间序列的外强迫因子的提取

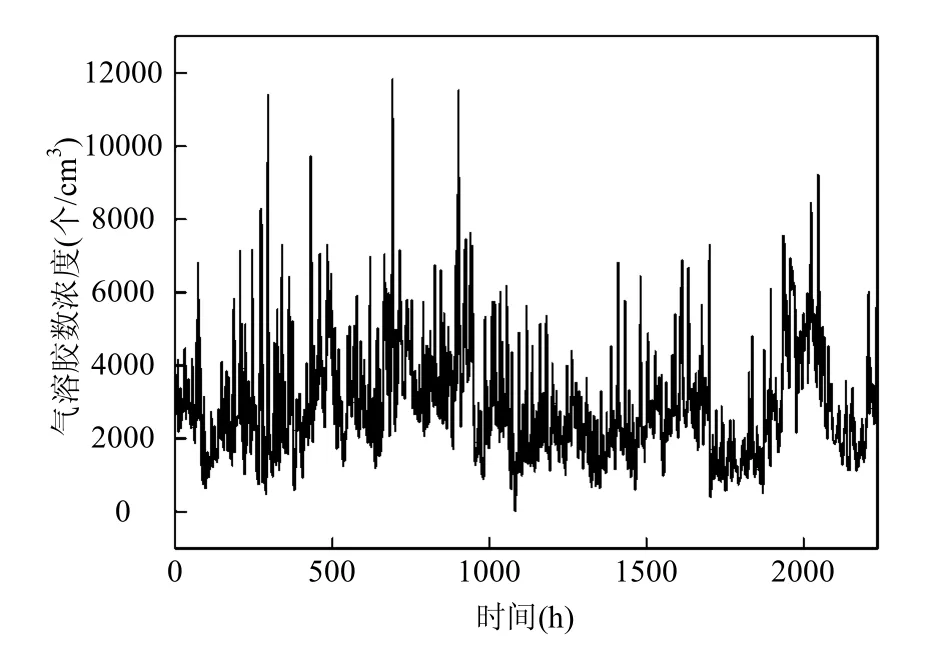
图1 黄山山底大气气溶胶数浓度Fig.1 Atmospheric aerosol number concentration time series at the foot of Huangshan Mountain

图2 不同嵌入维数情况下提取的外强迫因子Fig.2 External forcing factors extracted under different embedding dimension

利用SFA方法提取黄山山底大气气溶胶数浓度时间序列的外强迫因子.图1是2011年6月1日至2011年9月14日黄山山底每小时的大气气溶胶数浓度值时间序列.选取不同的嵌入维数，从黄山山底大气气溶胶数浓度时间序列中提取其外强迫因子.图2为嵌入维数分别为1、2、3、5、7、9得到的外强迫信息.从图2中可以看出，在一定范围内选取不同的嵌入维数对外强迫因子随时间变化差别不大.不同的嵌入维数所产生的外强迫因子随时间变化趋势相同， 表明SFA方法对于嵌入维数的依赖不敏感.

2.3 大气气溶胶数浓度时间序列预测试验

2.3.1 单一外强迫模式试验 拟预测2011年9月1日至9月14日每小时的大气气溶胶数浓度值.在预测试验中，将样本分为2段，前1898个数据用来构造预测模式中的映射，后336个数据用来检验预测效果.大气气溶胶数浓度时间序列的嵌入维数m1取为3，时滞参数τ取为1.由SFA方法从大气气溶胶数浓度时间序列中提取的外强迫序列的嵌入维数为m2，当m2=0所表达的含义是建立的预测模式中不包含外强迫因子，这时也被称为平稳性模式.当m2=1所表达的含义是建立的预测模式中包含外强迫因子，这时也被称为外强迫模式.为了检验预测模式的结果，分别做了10组试验，设定了不同的预报步数，在这个试验中预报步数1～10分别表示提前1h到10h预测大气气溶胶数浓度的变化.

图3 气溶胶时间序列预测结果对比Fig.3 Comparison of aerosol time-series forecasting results

图3分别是预报步数为1，4，7，2011年9月1日～9月14日每小时的大气气溶胶数浓度预测结果与观测值的对比.

为了更加明显比较这2种模型的预测能力，它们与观测数值的差值见图4，从图4可以看到外强迫模式的振荡幅度小于平稳性模式，也就是说外强迫模式得到的预测值更接近观测数值.

图4 2种预报结果与观测序列的差值Fig.4 The difference between the two kinds of forecast results with the observational sequence

图5 相关系数的比较Fig.5 Comparison of correlation coefficients

由图5可以看出，2种预报模式与实际观测数据的相关系数都随着预报步数增加而降低.此外，预报步数相同时，外强迫模式的相关系数总是大于由平稳性模式得到的相关系数.当预报步数为提前1h的时候，平稳性模式的预测结果相关系数是0.6982，外强迫模式的相关系数是0.7390.当预报步数当预报步数为4h的时候，平稳性模式的相关系数是0.4393，外强迫模式的相关系数是0.7033.而当预报步数为7h的时候，它们的相关系数分别为0.3197及0.4712.从表1也可以看出，2种预报模式的均方根误差随着预报步数的增加都在增大.但是外强迫模式的预报均方根误差总是小于平稳性模式给出的均方根误差.这也进一步说明，在预报模式中直接引入由SFA方法重构的外强迫因子，能够明显的提高模型的预测能力，这也表明外强迫因子与状态空间变量具有同等重要的作用.

表1 均方根误差的比较Table 1 Comparison of root mean square error

2.3.2 双强迫模式试验 上述试验考虑利用SFA方法得到的最慢的特征分量作为一个外强迫因子.在下面的预测试验中，尝试考虑SFA方法得出的次慢输出信号，将该次慢输出信号也引入预报模式的建立中，形成双外强迫因子预测模式，简称双强迫模式.双强迫因子预报模式的具体预测思路是：利用SFA方法得到最慢和次慢的信息，也就是两个外强迫因子的时间序列｛αi｝和｛βi｝，并且.将大气气溶胶数浓度时间序列和2个外强迫因子序列嵌入到m1+m2+m2维的状态空间中，得到如下的状态轨线：

图6 3种模式的预报结果对比Fig.6 Forecast results for the three models

并且可以建立如下的预测模型：

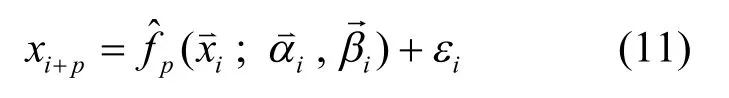
为了叙述方便，将不包含外强迫因子变化的模型称作平稳性模式，将包含单一外强迫因子变化的模型称作外强迫模式，而将包含两个外强迫因子变化的模型称作双强迫模式.

图6是预报步数为1、4、7时3种预报模式的预测结果对比，即在图3的基础上加入了双强迫模式的预测结果.

图7是3种预报模式的预测与观测的相关系数随预报步数的变化对比.结果表明，双强迫模式中第1步预报相关系数从0.6982提高到0.7475.当预报步数为4的时候，双强迫模式预报相关系数从0.4393提高到0.7197.当预报步数为7的时候，双强迫模式预报相关系数从0.3197提高到0.5057. 可以看出双强迫因子的预测能力在单一外强迫预测模式的基础上有了一定的提高.另外，跟前面的试验结果相比，也可以看出最慢的特征分量的贡献占显著作用.

图7 3种预报模式相关系数的对比Fig.7 Comparison of the correlation coefficients of three prediction models

3 结语

本文发展建立了与SFA方法结合的非平稳时间序列预测建模模型.与以往的预测模式人为设定的外强迫因子不同，而是从时间序列本身提取外强迫因子.通过平稳性模式、外强迫模式和双强迫模式3种不同预测模型，对黄山山底大气气溶胶数浓度时间序列进行预测试验研究.结果表明，外强迫因子与状态变量在预测中扮演同等重要的角色，它们的加入可以有效的提高预测技巧.

建立在SFA基础上的动力系统外部强迫的提取技术，是归因问题研究上的一个进展.利用SFA重构外强迫因子，并加入到预测模式中，虽然能有效地提高预测能力.然而，从本质上来说，它所提供的外强迫信息，只是从时间序列中作为数学方法的提出，并不能具体说明是这个外强迫信息所诠释的物理上的含义.这个问题的深入和扩展将是未来工作的方向.另外，针对外强迫信息的增加，可能对观测数据和质量提出新的要求.因此发展合适的预测建模技术也需要进一步的探讨和研究.

［1］杨培才，卞建春，王革丽，等.气候系统的层次结构和非平稳行为：复杂系统预测问题探讨 ［J］. 科学通报， 2003，48（13）：1470-1476.

［2］Yang Peicai， Bian Jianchun， Wang Geli， et al. Hierarchies and nonstationary in climate systems ［J］. Chinese Science Bullet，2003，48（19）：2148-2154.

［3］Manuca R， Savit R. Stationarity and nonsatationarity in timeseries analysis ［J］. Phys.D， 1996，99：134-161.

［4］Wang Geli， Yang Peicai， Bian Jianchun， et al. Forecasting methods with An external forcing factor of non-stationary time series ［J］. Chinese Science Bulletin， 2011，56（10）：1-4.

［5］Verdes P F， Granitto P M， Navone H D， et al. Nonstationary time-series analysis： Accurate reconstruction of driving forces ［J］. Phys. Rev. Lett.， 2001，87（12）：101-124.

［6］Wiskott L. Estimating driving forces of nonstationary time series with dlow feature analysis ［M］. 2003.

［7］Verdes P F. Global warming is driven by anthropogenic emissions： a time series analysis approach. ［J］Phys. Rev. Lett.， 2007，99（4）：1-4.

［8］Gunturkun U. Sequential reconstruction of driving-forces from nonlinear nonstationary dynamics ［J］. Phys. D， 2010，239（13）：1095-1107.

［9］Farmer J D， Sidorowich J. Predicting Chaotic time series ［J］. Phys. Rev. Lett.， 1987，59：845-848.

［10］Casdagli M. Nonlinear prediction of chaotic time series. Phys ［J］. D， 1989，35：335-356.

［11］Yang Peicai， Zhou Xiuji， Bian Jianchun. A nonlinear regional predict ion experiment on a short -range climatic process of the atmospheric ozone ［J］. Geophys. Res.， 2000，105（10）：12253-12258.

［12］陈伯民，纪立人，杨培才，等.改善月动力延伸预报水平的一种新途径 ［J］. 科学通报， 2003，48（5）：513-520.

［13］Wang Geli， Yang Peicai. A compound reconstructed prediction model for nonstationary climate process ［J］. Int. J. Climato，2005，25：1265-1277.

［14］陈潇潇，金莲姬，朱婧民.黄山山底大气气溶胶数浓度日变化 ［J］.中国环境科学， 2013，33（7）：1167-1173.

Prediction of the atmospheric aerosol number concentration using a new predictive technique.

CHEN Xiao-xiao1，2，3， WANG Ge-li1*， JIN Lian-ji2（1.Laboratory of Middle Atmosphere and Global Environmental Observation， Institute of Atmospheric Physics，Chinese Academy of Sciences， Beijing 100029， China；2.Nanjing University of Information Science and Technology， Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration， Nanjing 210044， China；3.Pingtan Meteorological Bureau of Fujian Province， Pingtan 350400， China）. China Environmental Science， 2015，35（3）：694～699

In the present study， a predictive technique incorporating driving forces was used to predict the atmospheric aerosol number concentration at the foot of Huangshan mountain which extractedthe driving force from the observation data by Slow Feature Analysis. To appraise its effectiveness， some prediction experiments were carried out using the hourly atmospheric aerosol number concentration in Huangshan. When the forecast step was 1， the correlation coefficient between the stationary model predictions and observation data was 0.6982； the correlation coefficent between the single external forcing model and observation data was 0.7390； the correlation coefficient between the double external forcing model and observation data was 0.7475. Adding external forcing can effectively improve the forecasting skills

slow Feature Analysis；external forcing driving；the atmospheric aerosol prediction

X513

A

1000-6923（2015）03-0694-06

陈潇潇（1989-），女，新疆吐鲁番人，助理工程师，硕士，主要从事非线性大气动力学研究.发表论文1篇.

2014-05-28

国家自然科学基金项目（41275087，41075061，41030962）；江苏高校优势学科建设工程资助项目（PAPD）

* 责任作者， 研究员， wgl@mail.iap.ac.cn