基于BP神经网络的证券市场异常波动识别模型

韩俊

（郑州大学，河南　郑州　450001）

基于BP神经网络的证券市场异常波动识别模型

韩俊

（郑州大学，河南郑州450001）

证券市场的波动是其本质特征和属性，但如果价格的波动性呈现出振幅剧烈、频率过快，就可能导致市场的价格扭曲，进而导致股票市场剧烈震荡.本文立足于实际的证券交易市场，建立多层神经网络分类器，使用BP神经网络中的四种学习算法对仿真数据进行拟合，结果表明弹性梯度算法对六种基本的波动模式识别精度较高.

证券市场；异常波动，BP神经网络；弹性梯度算法

证券市场的基本功能是引导资源合理配置，这一功能的发挥依赖于不断发生的证券价格波动，因此证券市场的波动是其本质特征和属性.虽然股票价格波动可以优化资源的合理配置，但是只有适度的波动才能奏效，剧烈的股市变化甚至会威胁到金融市场的稳定和经济的健康发展.因而，如何要减少股市交易过程中的异常波动，保障金融产品强壮性，这是对证券市场股价的股价异常模式进行有效地识别的首要目标［1］.

1　证券市场的异常波动模式

国外学者在证券市场的异常波动方面的研究比较多，而且已取得了较为丰富的成果.相比之下，国外成熟的市场经济国家利用政策性因素对证券市场进行干预和影响的频率相对较低，更多依靠市场自身的调节功能；我国的股票市场却呈现出较为明显的异常波动特征，一方面股市的波动严重脱离了企业业绩和宏观经济运行状况，另一方面从我国股市的波动幅度来看波动频繁而剧烈.

图1　证券市场异常波动模式图

图1给出了基于证券市场的异常波动情形.

当证券市场的股价在一定范围内随机波动时，证券市场处于正常运行状态，其变化趋势如上图（a）所示，称为证券市场波动的正常模式.周期异常则是证券市场的股价在一定时间段内呈现有规律的周期变化，如上图中（b）所示.当证券市场的股价呈现出明显地趋势、间接跳跃或周期循环的变化趋势时，表明当前的证券市场出现了异常状况，将会导致经济政策失灵股价约束失控的发生.证券市场的股价异常状况通常分为三类：趋势、阶跃和周期.其中，趋势异常指证券市场的股价会表现出上升或下降的变化趋势，如是图中的（c）和（d）所示.间接性阶跃异常是指证券市场的股价会呈现出向上阶跃或向下阶跃的状态，如上图（e）和（f）所示.因此，动态过程股价异常波动状态可划分为上升趋势、下降趋势、向上阶跃、向下阶跃和周期五种模式.

2　基于BP神经网络的证券市场异常波动识别模型

2.1BP神经网络简介

BP神经网络全称为Back-Propagation Network，即反向传播网络，比较常用传递的函数是logsig、tansig和purelin.

其基本原理是利用输出后的误差来估计输出层的直接前导层的误差，再用这个误差估计前一层的误差，如此一层一层地反传下去，就获得了所有其他各层的误差估计.BP神经网络以梯度下降算法为基础，在学习过程中不断地调整权值和阈值，使得实际输出值与输出期望值的误差达到最小.使用S型激活函数（logsig）时，BP网络输入与输出的关系为：

BP神经网络在使用过程中存在以下问题：1）需要较长的训练时间；2）易陷入局部极小值，对此可以使用改进后的BP神经网络.例如：附加动量法、弹性BP算法、共轭梯度法等［12］.

本文依托于BP神经网络，使用以下四种学习算法对证券市场的波动进行研究.如下表：

表1　常用算法表达式

梯度下降法（traingd）也称为最速下降法，使用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢.

有动量的梯度下降算法（Traindm）是在原有梯度下降算法中加入了“附加动量项”，即令，式中α为动量项，通常是正数.

有自适应学习速率的梯度下降算法（Trainda）是在原有梯度下降算法中加入了“自适应学习速率lr”，学习速率的调整公式如下：

弹性梯度下降算法（Trainrp）通常只取偏导数的符号，而不考虑偏导数的幅值.权值更新的方向由偏导数的符号决定，而权值变化的大小则由一个独立的“更新值”确定.

由于动态过程股价异常波动模式的各种异常样本数据呈现出不同的非线性变化形式，且具有较大的差别，为了选择适用于本文提出的BP神经网络识别框架中各学习算法的选择，下面将采用仿真实验方法，对上述四种学习算法的BP神经网络识别效率进行对比分析.

2.2多层BP神经网络分类器识别

基于BP神经网络的股价异常波动模式识别的具体识别步骤如下：

（1）通过NNW1进行粗略的分类，可直接分离出周期模式、正常模式，上升模式和下降模式分别分为一类.

（2）当NNW1分类器判断当前数据流为上升变化时，再利用NNW2分类器，将呈现上升趋势变化的数据流划分为上升趋势和向上阶跃两种股价异常波动模式.

（3）当NNW1分类器判定当前数据流为阶跃变化时，再利用NNW3分类器，将呈现下降趋势变化的数据流划分为下降趋势和向下阶跃两种股价异常波动模式.

基于上述的识别模型，BP神经网络的相关节点数据可设置如下：

表2　BP神经网络的相关设定

3　仿真实验

3.1实验数据的产生

文章中的数据产生采用蒙特卡洛方法 ［13］，仿真动态过程的数据x（t），仿真公式如下：

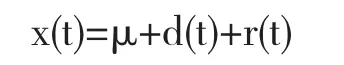
其中μ为动态过程的设计目标值.为了简化仿真数据，可设定μ为零.r（t）表示动态过程的随机因素变化，即r（t）～N（0，1）.d（t）表示动态过程质量异常数据的变化.

为了仿真动态过程只有随机因素干扰的正常模式，可用x（t）=r（t），r（t）～N（0，1）产生动态数据.对于上升趋势、下降趋势、向上阶跃、向下阶跃和周期五种质量异常模式，将分别按照以下公式产生仿真数据：

（1）异常模式1：上升、下降趋势

其中k表示上升或下降趋势的变化斜率，取值范围设定为0.2到0.5

（2）异常模式2：向上、向下阶跃模式

其中b表示证券市场股价发生阶跃的位置，b=（t-t0），发生阶跃前b=0，发生阶跃后b=1.t0表示证券市场股价发生向上或向下阶跃的时刻.s表示阶跃的幅度，取值范围设定为0.8到2之间.

3.2实验结果分析

通过上述的分析可对该数据进行相关的拟合训练，每个神经网络的相应的识别精度见下表.

表3　四种学习算法对应各个神经网络的识别精度

从上表中的结果可以看出不同学习算法下的神经网络系统对于不同的股价异常波动模式的识别效率不同，弹性梯度下降算法对于动态过程股价异常波动模式的整体识别效果较好，平均识别率达到了97.02%.这四种学习算法对于在NNW1粗略识别后，NNW2和NNW3中的第二次识别精度已基本达到98%左右.

然而，不同的学习算法对于六种基本模式的识别精度是不同的，对应于上面建立的模型，各个算法关于六种模式的识别精度如表4.

从表4可以看出，弹性梯度下降算法在不同的模式间识别精度是较高的，达到95.1%.在六种基本模式中，识别精度最高的是正常模式96.3%，最低的是周期模式89.6%.

表4　四种学习算法对应六种基本模式的识别精度

4　结论

通过实证实验，对比不同股价异常波动模式在不同学习算法下的神经网络识别精度，可以看出不同的异常模式在不同学习算法下的神经网络识别精度不同.根据实验结果，选择识别精度高的学习算法用于动态过程股价异常波动模式的BP神经网络识别模型，将对提高神经网络模型的整体识别效果起到作用.

本文的研究为动态过程的实时证券市场监控与诊断提供了方法，但考虑到实际问题的复杂性，本文还存在着以下的不足：

（1）证券市场是一个多方面非线性动力系统，影响股价变化的因素不胜枚举，本文仅仅从当日股市的收盘价入手，这显然是不够的.未来的研究应该考虑到引进股市的技术型指标从多方面进行考量.

（2）本文中仅仅是使用的BP神经网络中的几种不同算法，由于BP神经网络本身存在的缺陷，也许使用这几种算法并不能得到令人满意的结论.未来的研究应该使用神经网络和其他智能算法相结合的方式进行试验，这样试验结果拟合度才会更高.

〔1〕彭凌宇.我国证券市场发展现状与前景研究［J］.现代商业，Modern BusinessF832.51.

〔2〕赛英，张凤廷，张涛.基于支持向量机的中国股指期货回归预测研究［J］.中国管理科学，Chinese Journalof Management ScienceF724.5；F224；F832.51.

〔3〕袁晨，傅强.异质价格预期、无风险利率调整与证券市场波动 ［J］.管理科学学报，Journal of Management Sciences in ChinaF224；F832.51.

〔4〕张新红.证券市场预测的小波神经网络模型［J］.数量经济技术经济研究，Quantitative&Technica Economics，F224.

F830.91

A

1673-260X（2015）11-0077-03

河南省金融市场稳定性研究