耙吸船吸泥管作业过程的CFD仿真分析

丁艳坤宋军平刘　建

（1.中交机电工程局有限公司，北京100088；2.中交广州航道局有限公司，广州510221）

船舶营运

耙吸船吸泥管作业过程的CFD仿真分析

丁艳坤1宋军平1刘建2

（1.中交机电工程局有限公司，北京100088；2.中交广州航道局有限公司，广州510221）

耙吸挖泥船耙头吸口距海床表面高度和抽吸强度在保证开挖工程精度和在吸泥过程中不破坏海床结构中有很大的影响。利用流体-结构动态耦合数值模拟的方法，以“广州号”耙吸挖泥船为母船，仿真计算挖泥船吸泥工作过程耙头离地高度及流量变化对海床结构中土层的应力影响，以此来指导挖泥船的操作。计算结果将为确定耙吸挖泥船吸泥管工作工况提供依据。

吸淤；液固耦合；仿真计算

0　前言

在疏浚整治、航道开挖及维护、海底隧道和管沟挖掘，以及深海取沙等工程中，往往利用耙吸挖泥船施工，而耙吸挖泥船施工主要是由耙头破土，依靠泥浆泵和吸泥管（耙吸管）清除在海床上被挖的泥沙（余泥）。泥浆泵启动后，吸泥管在压差作用下借助水流冲刷，将海床上的泥沙（余泥）清除。清除速度与吸泥管流量、泥沙特性，吸泥管口的形状、位置有关。

为保证施工精度，需要合理控制耙头吸口的高度和抽吸强度，在吸余泥过程中不破坏海床本身结构。本项研究采用CFD数值计算的方法考察挖泥船吸泥管工作过程中海床结构的应力变化，目的是确定吸泥管工作时的适当工作方式。

本文主要以中交广州航道局有限公司的“广州号”耙吸挖泥船为母型船（泥浆泵、吸泥管和耙头）进行仿真分析。

1　吸泥管水流与海床结构应力分析原理

建立耙头、吸泥管、水体与泥层的三维计算模型，构造三维计算网格。按规定流量（或压差）计算吸泥管口的流动。选择合适的泥沙特性参数建立均匀泥介质数值模型模拟海床结构。

1.1土层强度分析［1］

土的抗剪强度是指土体对外荷载产生的剪应力的极限抵抗能力。在外力作用下土中一点的剪应力达到土的抗剪强度、土体的一部分相对于另一部分发生移动时，便认为该点产生了剪切破坏。工程实践和室内试验都验证了土受剪应力产生的破坏。剪切破坏是强度破坏的重要特点。如果吸泥过程中在耙头吸口入口处产生过大压强差，土体产生局部过大的、不均匀的变形就可能造成土层破坏。

一般认为剪应力是引起材料流动破坏的因素。这一类强度理论有最大剪应力理论（第三强度理论）和形状改变比能理论（第四强度理论）。它们以材料出现流动现象或发生显著的塑性变形作为破坏标志。最大剪应力理论认为，当外力过大，材料会沿着最大剪应力所在截面滑移，而发生流动破坏。按最大剪应力理论，材料内部一点处的最大剪应力τm应小于强度极限值。

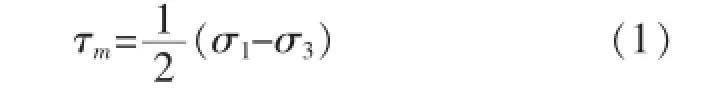
形状改变比能理论（第四强度理论）假设，无论在什么样的应力状态下，只要材料内部一点处的形状改变比能达到材料的极限就会引起材料的流动破坏。按第四强度理论建立的强度条件是von Mises应力应小于强度极限值。von Mises应力的定义为：

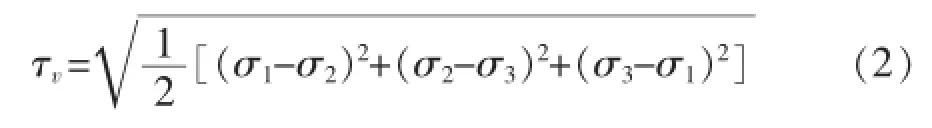
式中：σ1、σ2、σ3为三向应力状态的三个主应力。

土的强度机理主要是研究土体抗剪强度的构成因素与来源。通过土体抗剪强度的库仑定律可以知道，土体的抗剪强度主要来自两个方面：黏聚力和内摩擦力，但是不同性质的土体其强度机理亦有不同。

土的抗剪强度公式为库伦定律（Coulomb公式），即固体间摩擦力与彼此间的正应力的线性关系。

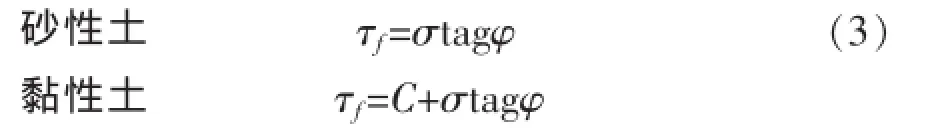
式中：τf——破坏面上的抗剪强度；

σ——作用在剪切面上的法向应力；

φ——土的内摩擦角；

C——内聚力，kPa；

φ和C称为土的总强度指标

抗剪强度指标φ和C反映土的抗剪强度变化的规律性。按照库仑定律，对于某一种土它们是作为常数来使用的。实际上土的抗剪强度不是定值，而是随作用在剪切面上的法向应力的增加而增加的。

对于无黏性砂土，由于土体颗粒较粗，其抗剪强度主要来源于颗粒间的摩擦阻力，即所谓的内摩擦力，常用内摩擦角来表征其大小。内摩擦力包括两个方面：

1）滑动摩擦力，即颗粒产生相互滑移时要克服由于颗粒表面粗糙不平而引起的摩擦力。滑动摩擦力的大小与作用于颗粒间的有效法向力、土颗粒的矿物成分等因素有关。

2）咬合摩擦力，即由于颗粒相互镶嵌、咬合及联锁作用而产生。另外，咬合摩擦力还和土的密实度、原始密度、颗粒级配以及颗粒形状等因素有关。

洁净的干砂黏聚力为零，非干砂土具有很小的黏聚力（一般不超过9.81 kPa）。这或者是由于砂土中有一些黏土颗粒，或者是因为砂土处于潮湿（但不饱和）状态，由于毛细水的作用而形成黏聚力。

砂土的内摩擦角取决于砂粒间的摩擦阻力以及联锁作用。一般可以取中砂、粗砂、砾砂的φ=32°～40°；粉砂、细砂的φ=28°～36°。孔隙比愈小，φ愈大，但是含水饱和的粉砂、细砂很容易失去稳定，有时规定取φ=20°左右。

对于黏性土，其土粒较细，所以其抗剪强度除了有来自颗粒间的内摩擦力外，还有一部分来自土粒间的黏聚力。黏性土的抗剪强度主要取决于黏聚力。黏聚力包括：

1）原始黏聚力，即土粒间水膜与相邻土粒之间的分子引力所形成的黏聚力。当土被压密时，土粒间的距离减小，原始黏聚力随之增大。当土的天然结构破坏时，会丧失原始黏聚力的一部分，但其强度会恢复一部分。

2）固化黏聚力。它是由于土中化合物的胶结作用而形成的黏聚力。当土的天然结构被破坏时会丧失这部分黏聚力，而且不可恢复。

黏性土的抗剪强度指标的变化范围很大，与土的种类有关；并且与土的天然结构是否被破坏、试样在法向压力下的排水固结、试验方法等因素有关，大致可以认为黏性土的黏聚力从小于9.81 kPa到超过200 kPa。

两个世纪以来，尽管土的强度问题的研究已得到很大发展，但这最基本的关系式仍广泛应用于理论研究和工程实践，而且也能满足一般工程的精度要求。

受力结构内同一截面上不同点的应力一般是不同的，而过同一点所取截面的方位不同其应力也是变化的。各向同性材料的三向应力状态中，三对相互垂直的单元面上剪应力为零，主应力为σ1、σ2、σ3（σ1＞σ2＞σ3），最大切应力τmax位于与σ2平行且与另两个主应力的方向成45°角的截面上，

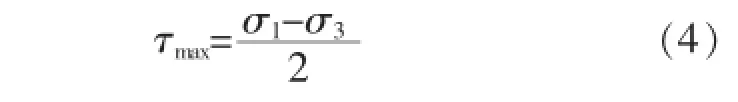
剪应力最大面上的正应力

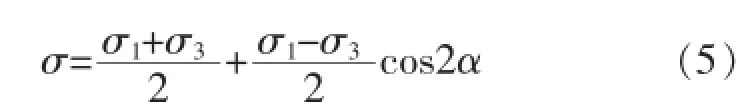
本项研究用CFD数值计算的方法考察吸泥管工作过程中海床土层结构内的应力变化，从应力状态分析得到土层结构邻近破坏点的工作条件。

破坏面与水平面的夹角为

破坏面上的法向应力和剪应力分别为

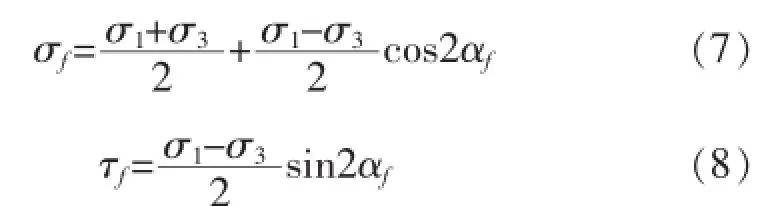
在土的抗剪强度公式τf=C+σtagφ中，当破坏面上的法向应力取有效应力时抗剪强度指标才是常数。有效应力等于法向应力减去孔隙内静水压强值。

1.2吸泥管内流动分析

吸泥过程中管内是泥沙和水组成的液固两相流。鉴于本文仅研究吸泥管内流动对于海床土层内应力变化的影响，为简化分析仅考虑单相水流产生的影响。

实际流体都是有黏性的，黏性应力阻滞流体的运动，消耗一定的运动机械能，所以，在黏性流体的运动过程中，流体的机械能沿着流动逐渐减小。机械能损失也称为水头损失，损失水头一般又包括沿程损失水头和局部损失水头两个部分。损失的能量由动力系统补充，以维持恒定流量的吸入过程。

吸泥管输送一定流量所消耗的机械能主要用于克服流动阻力（损失水头）和增加流体的重力势能。计算管道流动用到连续性方程和黏性流体总流的伯努利方程，就是为了确定损失水头。在层流状态下，沿等直径圆管道截面的速度分布为旋转抛物面，沿程损失水头与平均速度的一次方成正比。在湍流状态下，沿管道截面的速度分布远比层流均匀。根据黏性底层与管壁粗糙度的相对大小，又可以把管道中的湍流分为水力光滑管和水力粗糙管。在水力粗糙管中，沿程损失水头与平均速度的平方成正比。

管道截面的突然扩大或者缩小，管道系统中的半开阀门、分叉管以及弯管等会在局部形成流动分离和二次流，从而引起流体运动机械能的耗损。这种在局部区域内被耗散的运动机械能称为局部损失水头。一般需要通过实验提供的局部损失系数来计算局部损失水头。

海床土层内的应力随吸泥管口压强的变化而变化。根据伯努利方程知，吸泥管口压强与水流速度有关。水流速度分布与吸泥管流量、泥沙特性，吸泥管口的形状、位置有关。在计算中可以给定管口流量条件或压差条件作为边界条件。在一定的流量限制下，吸泥管内流动阻力越大、扬程越高，需要由泥浆泵提供的压差越大；反之，若泥浆泵提供的压差一定，吸泥管内流动阻力越大、扬程越高，管内流量则越小。

吸泥管作业过程的数值模拟和效率分析可以分成两步解决。首先计算出海床土层内的应力如何随吸泥口压强的变化而变化。在耙头吸口与吸泥管接口处给出规定的流量作为出口边界条件，计算出吸泥口压强分布和土层内应力分布。然后在规定的流量下计算吸泥管内的流动阻力和增加的流体重力势能，得到吸泥管系统所需功率。

2　数值模型和计算工况的设置

吸泥过程中流体运动和海床土层结构相互作用是流固耦合问题，采用大型动态耦合应力分析软件MSC.DYTRAN能够较好地实现流固耦合的数值模拟［2］。

本仿真分析将采用CFD计算的前处理软件MSC.PATRAN建立水体-土层三维耦合模型，再用MSC.DYTRAN直接求解流体NAVIER-STOKES方程和固体牛顿运动方程等微分方程，对水体和土层进行耦合分析，得到吸泥管作业时的应力分布。

2.1建立数值模型

根据实际尺寸，在前处理软件MSC.PATRAN中建立合适的水-吸泥管-土层三维物理模型，并在水体和土层间定义耦合计算模型。在物理模型中设置水体边界压强条件和吸泥管出口流量条件，在MSC.DYTRAN中计算土层和水体耦合作用下的应力分布。

2.1.1流体模型

流体模型称为欧拉网格模型，通过欧拉求解器来完成其计算。在欧拉方法中，网格是固定的参照系，流体材料的质量、动量和能量在网格中流动。由于流体和土层耦合运动的界面是变动的，建立模型的欧拉网格域要足够大，以能够容纳土层变形后的全体流动区域。图1是水体模型的三维欧拉网格。

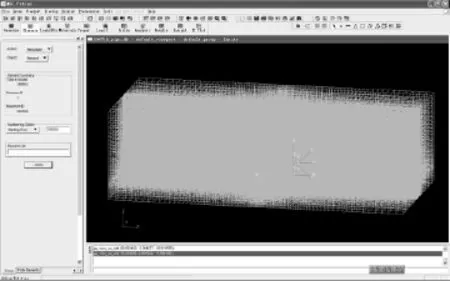
图1　水体模型的三维欧拉网格

在计算中吸泥管和耙头吸口结构部分以“广州号”耙吸船耙头及吸管尺寸为依据建立三维模型，作为约束水流的固体界面设计成壳单元（PSHELL），这些壳单元的空间位置是固定不动的。改变耙头吸口距离地基的高度位置时，重新设计这些壳单元的空间位置。这样处理需要较多的网格生成时间，但是比动态耦合计算节约了大量计算时间。图2为吸泥管的三维计算模型。图3是水体模型和吸泥管的三维计算网格图。

2.1.2结构模型

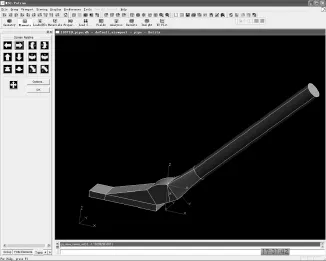
图2　吸泥管三维计算模型

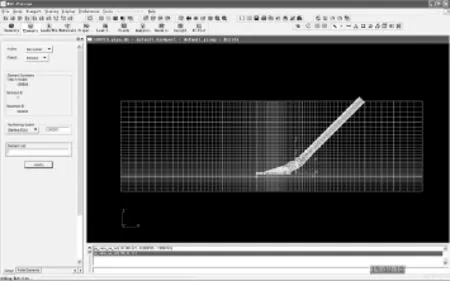
图3　吸泥管与水体的三维计算网格

结构模型称为拉格朗日网格模型。MSC. DYTRAN中的拉格朗日求解器主要用于对结构的分析以及对固体材料的分析，因此土层需要建立拉格朗日模型网格。当采用拉格朗日方法时，网格节点固定在分析对象上，当分析对象发生变形或位移时，节点随着材料的移动而移动，同时单元也随之发生变形。图4是海床土层的三维计算模型，图中还显示了吸泥管的位置。

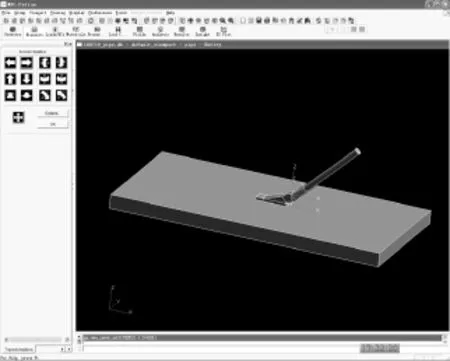
图4　吸泥管与海床土层的三维计算模型

吸泥管壳单元属于拉格朗日网格，设置为刚性材料和固定位置后，不参加应力分析，仅作为流体边界条件，即流体不可穿越的界面。

港珠澳大桥隧道基槽疏浚工程工法及技改方案指出：-29.5 m上下分别为淤泥质粉质黏土和粉质黏土。

3　约束和加载

3.1欧拉单元

对欧拉体施加载荷和约束的时候，欧拉约束作用于网格内的单元面上而不是网格点上。

流体的入口和出口根据水的参数定义相应的材料物理性质，以及流动界面的位置。通过FLOW条目TLOAD1调用，TLOAD1的TYPE栏必须设置为4。FLOW条目调用由CFACE，CFACE1或者CSEG条目指定面元集，材料流经这些面元。然后指定X、Y和Z方向的速度、压强、密度和流动材料的比内能。

欧拉单元的初始条件使用TICEL或TICEUL条目来定义，允许在分析之前初始化模型状态。TICEUL条目为欧拉网格的几何区域定义初始瞬态条件，并和PEULER1性质定义一起使用。根据工程实际给出相应的初始速度和压强等条件。

欧拉网格的计算域范围沿耙头吸口长度方向为20 m，横向10 m。初始水层深5 m，土层厚1 m。为保证土层变形后腾出的空间具有欧拉网格性质，欧拉网格在垂直方向为6 m，包括土层范围在内。由于欧拉网格数量巨大，采用变网格密度分布网格。

欧拉网格计算域上边界和侧面边界设置为流入的流动边界条件，按深度设置水静压值为压强边界条件。吸泥管出口处设置为流出的流动边界条件，按规定流量设置出口速度边界条件。

3.2拉格朗日单元

拉格朗日土层定义为弹塑性材料。拉格朗日单元的载荷定义使用TLOAD项。模型场重力使用GRAV定义重力加速度的大小和方向。

土层的拉格朗日网格为20 m×10 m×1 m。土层底面和侧面设置网格节点位移为零的边界条件。

吸泥管壳单元壁面设置为刚性壁，即流体不可穿越的界面。吸泥管出口面设置为给定流量的流体边界面。

3.3水体-土层耦合条件

根据土层与水体之间的耦合关系定义耦合面和相应的耦合算法。土层网格外边界的单元面设置为耦合面。使用流体与结构相互作用的耦合算法，目的是使采用欧拉网格或拉格朗日网格模型的材料能够互相作用。没有耦合的两个求解器是独立的，放在欧拉网格里面的拉格朗日单元不会影响欧拉材料的流动，欧拉材料也没有反作用力作用到拉格朗日结构。而耦合算法计算这两套单元的相互作用。从而可以分析复杂的流体与结构相互作用问题。

流体对土层的作用力通过耦合面作为土层的边界条件，从而影响每一时间步内土层的位移和应力分布。

借助SURFACE条目，在拉格朗日结构中定义一个多面元的面 （即土层表面），然后通过使用COUPLE条目激活的耦合算法，即可完成土层与水体之间耦合计算的设置。

3.4设置计算工况

港珠澳大桥海中桥隧主体工程总长约35 km（其中香港界内约6 km），采用桥隧组合方案（隧道长6.753 km，桥长25.947 km）。据设计文件介绍，海底隧道位于伶仃主航道和铜鼓航道地段。

勘察表明，沉管隧道开挖及穿越地层主要为淤泥、淤泥质黏土、流塑粉质黏土夹砂和软～可塑粉质黏土。地层以流～软塑黏性土为主，局部为软～可塑黏性土和中密粉砂。盾构隧道穿越地层有淤泥、淤泥质黏土、流塑粉质黏土夹砂、软～可塑粉质黏土及粉～粗砂层。隧道主要自中密～密实砂土层中穿过，详见表1。

根据对场区各岩土层室内物理力学试验和原位测试结果的分析统计，结合野外鉴定、前期勘探成果和地区经验［3］，按文献［4-5］推荐的力学参数换算方法，计算工况的设置。

1）根据隧道开挖及穿越地层的主要土层力学参数进行计算。主要有淤泥，淤泥质黏土，粉质黏土夹砂和粉质黏土等类型。

2）根据初步计算结果，在一定范围选择耙头吸口安装高度。

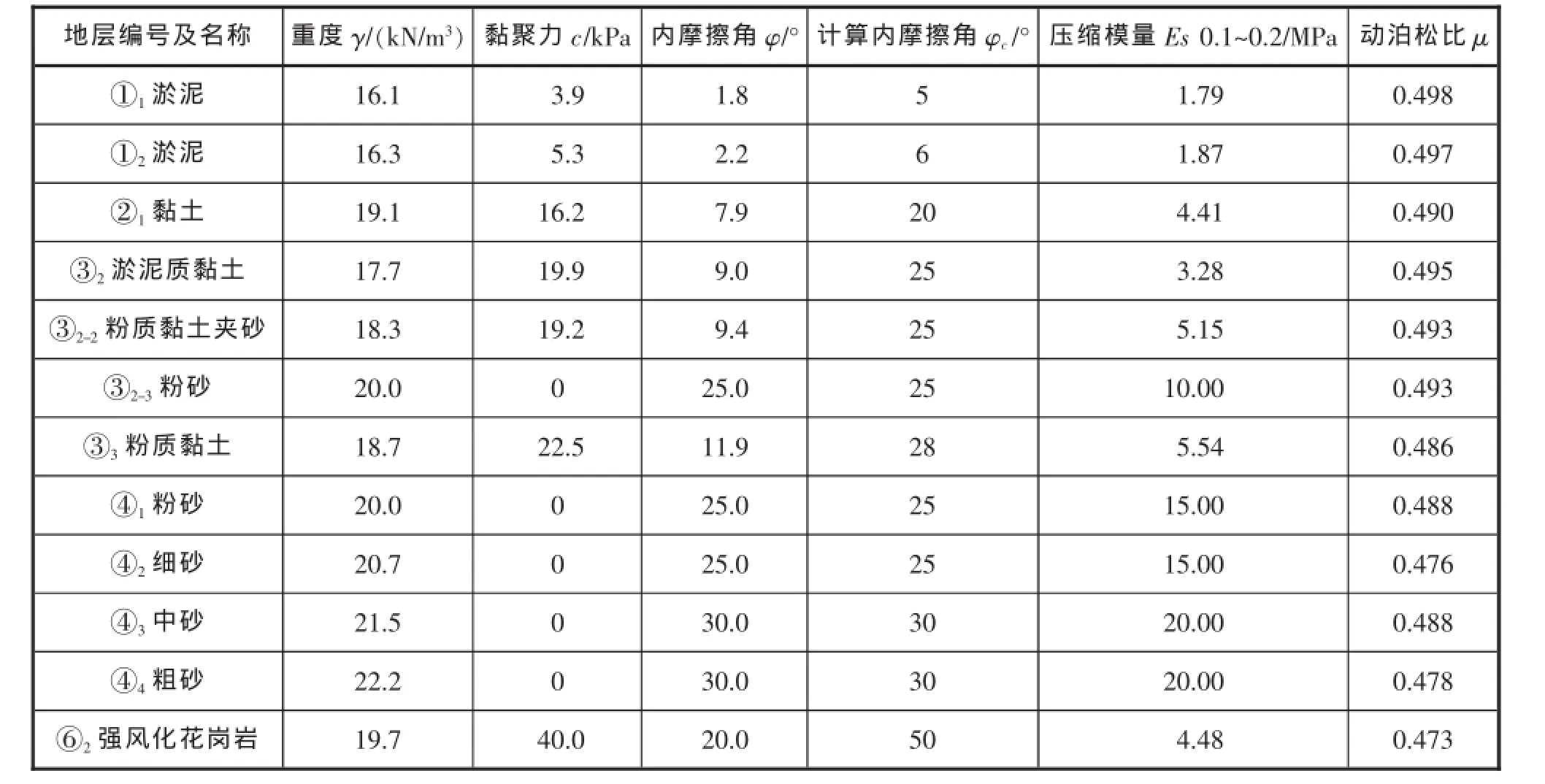
表1　《桥址区软土主要物理力学性质表》（部分摘录）

4　计算结果

4.1吸泥管水流运动特性

初始条件按水深度设置静水压强分布，避免由于压强分布与实际情况差别太大引起强烈冲击波，造成计算失稳。图5为某工况水体初始压强分布。图6为某时刻耙头吸口内流体速度分布和土层内的应力分布图。图7为某工况耙头吸口进口处流体速度分布。图8为某时刻水体纵断面（包括吸水头和吸水管）内流体速度z分量的分布。

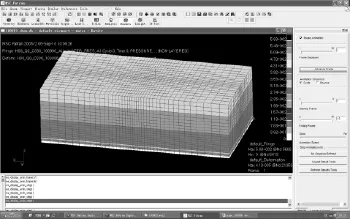
图5　水体初始压强分布　

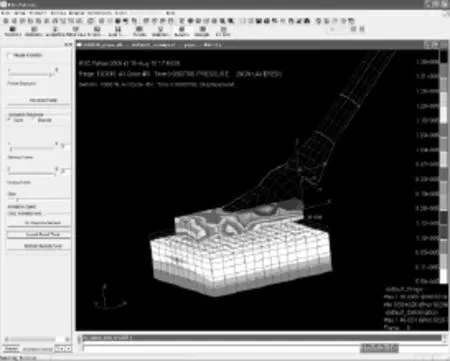
图6　某时刻耙头吸口内流体速度分布和土层内的应力分布

图7　耙头吸口进口处流体速度分布进口面积的1/4。左下为进口面的中心

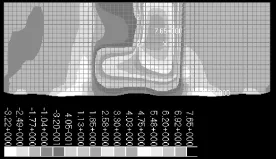
图8　某时刻水体纵断面（包括吸水头和吸水管）内流体速度z分量的分布

4.2土层应力分布特征

以曲线形式给出计算稳定以后得到的应力的时间平均值的分析结果。其中，主应力、von Mises应力、破坏面上的应力和剪切强度指标等都需要经过再计算得到。

土层应力分析给出相关的最大、最小主应力，最大剪应力τm，von Mises应力τv和破坏面上的剪应力τf。以海床底面为水平方向的X、Y坐标，垂直向上为Z坐标方向。土层中的应力在这三个坐标方向主要是法向应力，三个坐标平面内的剪应力较小。图9为耙头吸口进口离海底床面0.8 m，正对耙头吸口进口的床面土层内的法向应力分量Txx（yoz平面内，沿x方向的分量）的时间变化曲线。刚开始计算时波动较大，然后趋于稳定，在对应深度静水压强的量级上小幅振荡。计算取床面深度为45 m。计算到20 s以后取各应力分量的平均值进行计算。

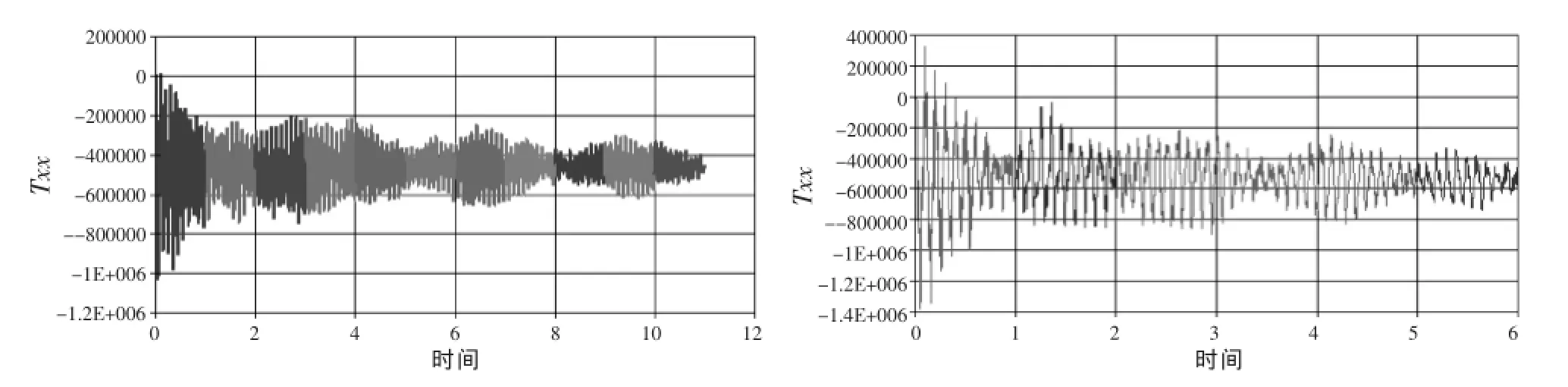
图9　耙头吸口下方土层内的法向应力分量Txx的时间变化曲线耙头吸口进口离海底床面0.8 m，流量为5 m3/s

以发生最大应力单元的数据计算抗剪强度指标并进行比较。根据土体抗剪强度的库仑定律计算抗剪强度指标，计算结果列于图10。图中比较各工况耙头吸口下方土层内最大破坏面剪应力和抗剪强度指标。破坏面剪应力随耙头吸口与海床面距离变化，图中标出的流量单位为m3/s。图中空心符号为破坏面剪应力，实心符号为计算的抗剪强度指标。

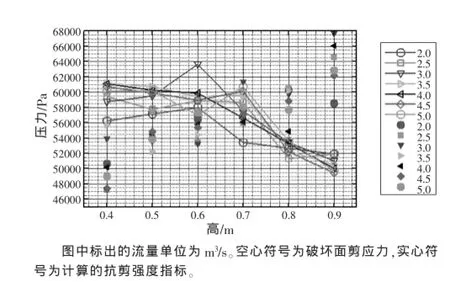
图10　各工况耙头吸口下方土层内最大破坏面剪应力和抗剪强度指标

5　计算结果分析

按照《港珠澳大桥地质勘查报告》中提供的淤泥质黏土（3-2）和粉质黏土夹砂（3-2-2）两种土质的数据范围设置参数进行计算（表1）。考虑到还需要孔隙内静水压强等参数，其中一组工况的土数据为：密度1 907 kg/m3，黏聚力22.5 kPa，计算内摩擦角25°，孔隙内静水压强135.6 kPa，压缩模量831 kPa，泊松比0.486。

本研究分析计算了吸泥管流量（2～5）m3/s，耙头吸口进口面离海底床面（0.4～0.9）m的几种工况，床面深度45 m。按数值模拟得到的土层应力数据计算土层破坏剪切强度指标，判断相应工况的土应力是否达到破坏限度。

图10表明，耙头吸口距离土层的不同高度对于土层是否破坏有显著影响。当耙头吸口离土层高度在0.5 m以下，各流量下（2.0～5.0 m3/s）土层破坏面上的剪应力均超过剪切强度指标；当耙头吸口离土层高度在0.8 m以上，各流量下（2.0～5.0 m3/s）土层破坏面上的剪应力均小于剪切强度指标；当耙头吸口离土层高度在0.6～0.7 m之间，土层破坏面上的剪应力过渡为超过剪切强度指标。

从上述仿真分析可得出初步结果：当耙头吸口离土层高度在（0.6～0.7）m之间进行吸淤施工作业是合适的，这时进行吸淤施工作业，不会破坏原状土，满足施工需要。

不同土质的抗剪强度不同。本研究是根据两种土质的数据范围设置参数［3］进行计算，并得出上述分析结果。在实际施工中，还需根据实际土质，适当调整耙头吸口距离土层的高度，以保证吸淤施工质量。

6　结语

本研究是以“广州号”为母型船（泥浆泵、吸泥管和耙头）进行仿真计算分析，本成果也可推广应用于相似的耙吸船的吸淤施工作业中。对于不同的耙吸船（泥浆泵、吸泥管和耙头），我们也可重新建立数值仿真模型，进行仿真计算，推断其吸淤施工状态，提出施工建议。

［1］赵树德.土力学.高等教育出版社，北京：2001.

［2］MSC Software Corporation.MSC.Dytran Reference Manual［M］.Version 2005，Printed in U.S.A.

［3］港珠澳大桥地质勘查报告.

［4］JTG D70-2004.公路隧道设计规范.

［5］GB 50307-1999.地下铁路、轻轨交通岩土工程勘察规范.

CFD Simulation Analysis for the Suction Pipe Working Process of the Trailing Suction Hopper Dredger

Ding Yan-kun1Song Jun-ping1Liu Jian2

（1.CCCC Mechanical&Electrical Engineering Co.，Ltd.Beijing 100088，China；2.CCCC Guangzhou Dredging Co.，Ltd.Guangzhou 510221，China）

The height of the suction pipe and the setting of suction power of a trailing suction hopper dredger played a significant role to ensure the excavation precision and to protect the seabed structure from damage.A fluidstructure dynamic coupling numerical simulation was performed for the“Guangzhou”trailing suction hopper dredger.The relationship among the dredger dredging harrow head height，the setting of suction power and the stress status in the soil layer of the seabed structure were studied，which served as guidance for dredger operation.

sediment absorption；liquid-solid coupling；simulation calculation

U674.31

A

1001-4624（2015）01-0010-08

2015-04-14；

2015-05-30

丁艳坤（1966—），男，工程师，从事船舶建造和管理工作。宋军平（1969—），男，助理工程师，从事船舶建造和管理工作。刘建（1966—），男，高级工程师，长期从事港口疏浚和运营管理工作。