基于matlab的少齿差行星齿轮减速器的优化设计

王冬梅

基于matlab的少齿差行星齿轮减速器的优化设计

王冬梅

项目来源：上海市重点学科建设：机械设计制造与自动化

王冬梅

上海电机学院

王冬梅（1968-）女，博士，副教授，上海电机学院。研究方向：现代机械设计方法学。

本文采用现代优化设计方法针对少齿差行星齿轮减速器进行了主要参数设计。根据设计要求，确定了减速器的齿数差，建立了目标函数及性能和边界约束条件，利用matlab软件的优化工具箱对减速器进行了模数和齿数的优化设计，最后通过传统设计方法与优化设计方法的结果比较，说明了优化设计方法是一种提高效率，节约成本的有效优化途径。

概述

渐开线少齿差行星齿轮减速器因为结构简单、承载能力高、寿命长、具有较高的机械传动效率、运转平稳、噪声小、成本较低等特点，广泛应用于国民生产的各个部门。以经验类比为基础的传统设计方法，不仅使减速器设计效率低，而且很难得到最优化的设计方案。本文利用优化设计理论及matlab优化函数，对少齿差减速器进行优化设计。

建立优化设计模型

设计要求

某机器需设计一少齿差行星齿轮传动减速器 ，输入转速n=1200转/min，传动比为100，其额定输出转矩T=700Nm，工作平稳

确定齿数差

如齿数差增大，减速器的径向尺寸虽增大一些，但转臂轴承上的载荷可降低很多；并且由于齿轮直径的增大，从而可使轴承的寿命得到显著提高；此外，对减速器的效率、散热条件等也有了一定的改善。因减速器传递的功率不大，决定采用三齿差。齿数差

建立目标函数

（1）建立优化设计的数学模型

依照优化设计的要求，近似地取少齿差行星齿轮的体积之和的最小（即质量最小）作为目标函数，体积计算公式如下：

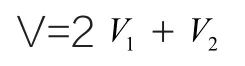
z1，z2分别是行星轮和内齿轮的齿数；b为行星轮的齿宽，m为他们的模数。

从总体积计算公式可知，影响它的独立参数有行星齿轮的齿数z1，内齿轮的齿数z2，齿轮的模数m及齿轮的齿宽b，故该减速箱的优化为3维优化问题，因此取设计变量：

建立约束条件

约束条件包括性能约束和边界约束。性能约束包含接触强度、弯曲强度。边界约束包括齿宽系数、模数、齿轮齿数、传动比限制、结构干涉限制等等。

（1） 齿面接触强度条件

（2）齿根弯曲强度条件

同理：

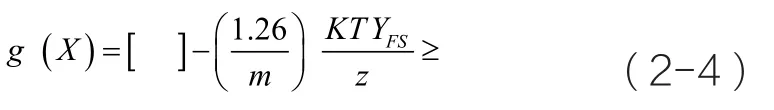
在这里，内齿轮的齿数比行星齿轮大3。

（3）设计变量的边界条件

小齿轮不发生根切的最小齿数条件：

g5（X ）=Z -17 〉 0（由设计下限保证） （2- 5）对模数的限制条件：

g6（X ）=m〉2.0mm（由设计下限保证）（2- 6）对齿轮的限制条件：为了保证齿轮承载能，且避免载荷沿齿轮分布严重不均，要求由此得：

综上所述，该减速器追求体积最小的优化设计数学模型是一个3维非线性约束优化问题。

运用MATLAB优化工具箱求解

（1）编辑目标函数M文件

function ［f，g］ = gear（x）

hd=pi/180；

a1=hd* x（2）.^2* 2*x（3）*x（1）.^2/4；

a2=hd* x（2）.^2* （x（1）.^2+9+6*x（1））*（2* x（3）+10） /4；

f=a1+a2；

（2）编辑目标函数约束条件

c（1）=17-x（1）

c（2）=2-x（2）

c（3）=6-x（3）/x（2）

c（4）=x（3）/x（2）-20

c（5）=180-x（2）^3*（x（1）+3）

c（6）=10.8-x（1）

（3）然后在命令窗口调用优化函数并用原始方案x0 = ［33.0； 4.0； 29.0］作为初始点进行求解；

x0 = ［33.0； 4.0；29.0］；

options = le-6；

x=constr（‘gear‘，x0，options）；

fprintf（1，‘x=％3.4f ‘，x）；

运行结果如图1下。

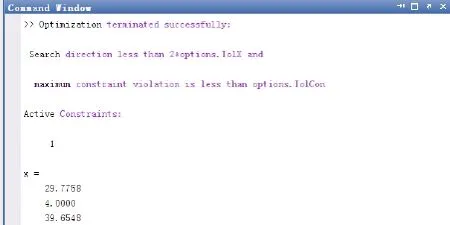
图1 matlab计算结果

经过圆整处理后可得：z=30 m=4 b=30。

优化设计与传动设计分析比较

优化设计计算结果

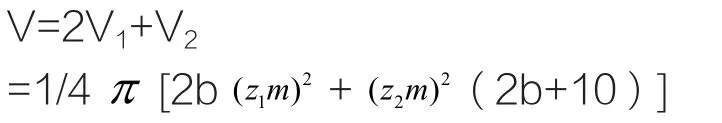
传统设计计算结果

采用传统设计方法可得到Z1=33，m=4，B=29，则

优化设计与传统设计的比较分析

传统设计优化后数据单位Z 33 30 mm m 4 4 mm B 1.636518x106mm329 30 mm V 1.90116 x 106

由上表我们可知，以齿轮体积最小对减速器进行优化设计的参数对比，优化后体积减小了：

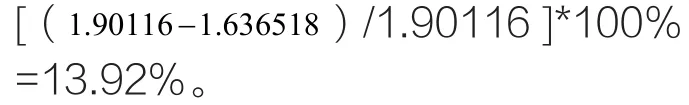
结语

应用MATLAB优化工具箱对少齿差行星齿轮进行优化设计，可大大缩减程序量，提高优化效率和精度，可有效减少行星齿轮的体积，从而使其重量减轻，成本降低为少齿差行星齿轮传动结构提供了一种优化途径。

10.3969/j.issn.1001-8972.2015.01.063