激光散斑法表面粗糙度测量的实验研究

刘国军

激光散斑法表面粗糙度测量的实验研究

刘国军

浙江省教育厅项目（Y201016456）

刘国军

山东理工职业学院 汽车工程学院

刘国军，男，1978年出生，本科学历，工学硕士，讲师，在山东理工职业学院从事教学科研工作，担任教务实训处副处长 ，研究方向：汽车检测技术，机械零件几何特征光学测量，车辆工程。

光学散斑法是一种较新的表面粗糙度测量方法，因其非接触、面采样、装置简单等优点而得到广泛关注。为探讨光学散斑法工程应用的可行性，利用标准研磨样块对光学散斑法中的两种方法：散斑对比度法及空间平均散斑法进行了实验。结果表明，两种散斑法均可用于表面粗糙度测量，而空间平均散斑法给出了特征参数与表面粗糙度的严格定量关系，可得到更可靠的测量结果。

表面粗糙度作为机械零件表面质量的一个重要表征参数，决定了工作面的密封配合性、耐磨耐蚀性及机器的可靠性与寿命。目前表面粗糙度测量技术大致分为两类：一类为轮廓技术，包括触针法、干涉测量法等。另一类为参数技术，给出被测表面的统计特性信息，有光散射法、散斑法等。

实际生产中，希望实现被加工件的100％检测，以减少废品率。轮廓技术需采用扫描法测量，故效率低，难以适应现场测量。而参数技术采用面采样，测量效率高，经适当改进，可用于工程中的在线应用，其中光学散斑法具有最大可能性。该方法属非接触测量，能有效避免工件表面的损伤。同时，对工作条件要求低，装置简单，易于在现场实现。基于上述考虑，本文针对两种散斑技术：散斑对比度法及空间平均散斑法进行实验研究，探索光学散斑法用于工程测量的实用性。

理论基础

散斑对比度法

散斑对比度用于表面粗糙度测量最早始于Sprague的散斑实验，当表面粗糙度与光源相干长度的量级可比拟时，散斑对比度与表面粗糙度是相关的。Fujii与Asakura小组的研究结果证实了Sprague的实验结论，并提出一种粗糙度测量新技术：在一定范围内，用表面粗糙度的标准偏差与光强起伏间的线性关系来检测表面粗糙度。

散斑对比度定义为强度标准差与强度平均值的比值，如下式所示：

式中V代表散斑对比度，I代表接收屏处某点光强，〈〉表示系综平均。

该技术可用于同种材料工件简单加工过程的表面的识别，经进一步研究可以用于在线测量。其缺点是测量范围较小，但可通过增大入射波长及入射角来扩大测量范围。

空间平均散斑法

该方法由Zhao等提出，通过引入Goodman散斑场局部遍历假设，对散斑图像进行分割，经空间平均运算即可提取表面粗糙度特征参数，该特征参数与均方根粗糙度关系为：

式中Vimage为粗糙度特征参数，是可测量；k=2π/ λ为波数；θ为入射角；σz为均方根粗糙度；Cimage可视为常数，与光学系统布置有关；“—”算符代表空间平均。为在实际中应用方便，利用自然对数运算将式（2）换算为线性关系：

上式即建立了特征参数Vimage与粗糙度参数σz2的严格线性对应关系。当光学系统的参数确定，则Vimage与σz一一对应。

实验及分析

实验过程

图1所示为实验装置图。He-Ne激光器波长0.6328μm，入射光束照射待测工件表面后，被表面散射，在反射方向设置接收屏来接收散斑图样并采用CCD相机进行记录。在相机设置中，需经过实际测试来确定具体曝光时间。标准样本采用哈量生产的平面研磨标准块组件。

测量步骤如下

调整激光器出射光束，使其在样块表面上的入射角为45°，微调样本支架高度及俯仰角度，使散斑图样进入相机的预定视场。

每个表面样本取不同区域6个测点，每个测点至少拍摄1幅散斑图像及1幅背景图像。同一样本同一测点拍摄一幅散斑图像后，立即遮住激光器入射光，拍摄一幅背景图像。下一测点重复上述操作。拍摄背景图像是考虑测量过程中难免有环境干扰，如周围光线明暗变化、激光器功率漂移、相机电子噪声等，当散斑图像减去相应的背景图像后，可以一定程度减少环境噪声影响。

所有样本图像采集完毕后，利用自编Matlab程序搜寻散斑区域并截取图像，对图像进行滤波，提取表面粗糙度特征参数。

结果分析

图2所示为CCD相机拍摄的一组散斑图像，每个子图左下角标明了标准样块的粗糙度值。对每个样块6个测点的散斑图像进行散斑对比度及空间平均散斑特征值的计算，所用计算式为：

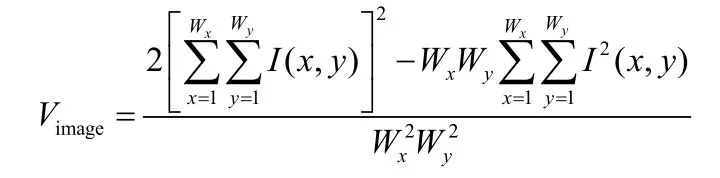
图1 实验装置图

图2 标准样块形成的散斑图像

式中，SC代表散斑对比度，Vimage代表空间平均散斑特征参数，Wx、Wy为图像的像素尺寸，I（x，y）表示像素点（x，y）处的光强（用0～255的灰度值表示）。

图3、图4为实验得到的曲线，图中横轴采用粗糙度Ra值。由图3看出，随着表面的粗糙度值增大，散斑对比度值随之增大，与Ra值呈现近似线性关系。为便于对未知粗糙度进行预测，对散点进行直线拟合，亦绘于图中。由于散斑对比度法无显式表达式，因此，直线拟合或许并非最理想的拟合方式。只有利用更多标准样本进行实验，才能得到更可靠的拟合曲线。图4（a）为空间平均散斑法中的Vimage值与Ra值的关系曲线，图4（b）为Vimage的自然对数值与Ra2的关系曲线。可以看出，实验结果与理论式（4）结论吻合，二者呈现较明显的线性对应关系，因此，仍采用线性拟合。与图3相比，图4（b）中的线性关系更为明显，而且由于具有理论表达式，在工程实用中，空间平均散斑法将比散斑对比度法更为有效。由图4可以看出，空间平均散斑法的结果仍有一定误差，造成误差的原因可能有：（1）可获得的标准样本数目有限，只能得到4个拟合点，这是误差产生的一个最主要的原因；（2）激光光源的功率波动，在散斑图像记录中引入随机噪声；（3）周围光线变化，降低了图像信噪比；（4）相机的电子噪声及热噪声，同样引起散斑图像噪声增大。

图3 散斑对比度值随Ra变化的散点图及直线拟合

图4 空间平均散斑表面粗糙度特征值的实验曲线

结语

散斑对比度法与空间平均散斑法是两种有效的表面粗糙度测量方法，具有非接触、易实现的优点。散斑对比度法的理论基础建立在系综平均的基础上，在工程应用中，为使测量容易实现，可用空间平均值代替系统平均值，但这会引入一定的误差。空间平均散斑法具备空间平均运算的理论依据，可直接用于工程实际，仅用一幅图像即可得到粗糙度特征参数。两种方法经适当改进，均具备应用于在线测量的前景，而空间平均散斑法因具有定量测量的理论前提，有望获得比散斑对比度法更可靠的测量结果。

10.3969/j.issn.1001-8972.2015.01.003