一种可鉴别的稀疏保局投影算法
2015-11-12苟建平詹永照张建明沈项军
苟建平,詹永照,张建明,沈项军
(江苏大学计算机科学与通信工程学院,江苏镇江212013)
一种可鉴别的稀疏保局投影算法
苟建平,詹永照,张建明,沈项军
(江苏大学计算机科学与通信工程学院,江苏镇江212013)
为了增强高维数据在低维子空间中的模式识别能力,假设任意2个类别相同的相似样本其稀疏表示也相似,并基于SPP和LPP思想,提出一种可鉴别稀疏保局投影降维新方法DSLPP.该方法通过稀疏表示学习和保局部投影,使得在投影子空间中不仅能够保持稀疏表示对数据很好的表达能力,而且较好地获取高维数据所蕴含的本质局部流形结构和自然判别信息,从而增强高维数据在子空间中的表示能力和可鉴别能力.在3个典型的人脸数据集Yale,ORL和PIE29上,将所提出方法DSLPP与PCA,LPP,NPE和SPP进行对比试验.结果表明DSLPP是一种有效的降维方法,能够较好地改善高维数据在低维子空间中的分类效果.
可鉴别稀疏保局投影;稀疏保持投影;保局部投影;稀疏表示;降维;模式分类
doi∶10.3969/j.issn.1671-7775.2015.06.013
近年来,稀疏表示已成为模式识别与计算机视觉领域广泛关注的热门话题之一.稀疏表示的基本假设是输入信号在一个过完备系统中求解一个最稀疏或者接近稀疏的表示,在信号压缩与编码[1]、图像恢复[2]方面取得了显著的成果.由于稀疏表示具有较好的数据表达能力和自然判别能力,其在人脸识别[3-4]、图像分类[5]、视频语义分析[6]等模式分类问题中得到了广泛应用,并取得了较好的分类效果.
在模式分类问题中,降维技术是的一个重要的处理过程.目前,降维技术主要包括线性和非线性2类方法.线性方法主要有主成分分析(PrinciPal com-Ponent analysis,PCA)、线性判别分析(linear discriminant analysis,LDA)和保局部投影(locality Preserving Projections,LPP)[7]等,非线性方法主要有基于核的KPCA,KLDA,KLPP等方法和基于流形的等距特征映射(isometric feature maPPing,ISOMAP)、拉普拉斯特征映射(LaPlacian eigenmaP,LE)、局部线性嵌入(locally linear embedding,LLE)等方法.这些典型的降维方法几乎都可以统一在图嵌入框架下,称为基于图的降维方法[S].其中,最为典型的图嵌入方法是LPP和保近邻嵌入(neighborhood Preserving embedding,NPE)[9],2者的主要思想都是基于近邻构图方式,构造一个局部邻接图,通过投影转化,将高维数据的这种局部结构保持在低维子空间中.LPP和NPE本质上是线性的流形学习方法,LPP是LE的线性扩展,NPE是LEE的线性扩展.
鉴于稀疏表示对数据具有很好的表达能力和自然判别能力,它在降维技术中的应用取得了成功.稀疏保持投影(sParsity Preserving Projections,SPP)就是一种典型的基于稀疏表示的无监督降维方法[10].针对在LLE,LPP等一些图嵌入学习算法中,依靠局部的K-近邻构图的局限性,SPP采用稀疏表示构图,自动选择样本的近邻个数,并且定义类似于NPE的目标函数,获得一个低维的子空间投影.该投影在保持数据的旋转、尺度和平移不变的内蕴特征的同时,还具有自然的判别能力.基于SPP的主要思想,一些研究者在SPP的基础上,提出了一些其他的稀疏降维方法[11-12],这些方法主要将样本的类别信息加入到稀疏表示学习中,从而增强了数据降维后模式之间的判别能力.
尽管SPP及其他稀疏降维方法在低维空间中保持了高维数据的一些内在几何特性和自然判别信息,并取得了良好的分类效果,但是由于未充分考察数据的局部几何特性,数据隐含的本质流形结构以及潜在的判别能力没有得到充分的获取,这在一定程度上降低了识别的性能.
文中基于LPP的保持数据局部结构特点,并借鉴SPP和LPP思想,提出一种可鉴别的稀疏保局投影算法(discriminative sParsity locality Preserving Projections,DSLPP).在DSLPP算法中,首先通过稀疏学习,获得每个训练样本优化后的稀疏表达.其中,稀疏表示系数矩阵具有在一定程度上反映了数据的内在几何属性和潜在自然判别能力特点.根据文献[13]可知,稀疏表示学习独立的对每个特征样本进行编码,由于过完备和足够的字典,相似的特征可能得到完全不同的稀疏编码去表达,这将导致数据局部信息的损失.为了保持这种局部信息,以及充分利用稀疏矩阵所具有的特性,DSLPP基于LPP保局部的思想,假定类别相同的2个相似样本在稀疏表达后也相似,且投影在低维的子空间中也应尽可能地保持相似,从而使得高维数据的局部几何结构较好地保持在子空间中,并增强高维数据在子空间中的判别能力.为了验证所提DSLPP算法的有效性,文中在3个典型的人脸数据库上进行对比试验.
1 相关的工作简介
1.1保局部投影算法LPP
保局部投影算法LPP[7]是一种保持数据局部结构的线性降维方法.LPP主要是通过构造高维数据的局部邻接图,并在图嵌入学习过程中保持这种局部的近邻关系,其算法实现过程如下.
1)近邻构图.采用K-近邻方式构建数据的邻接图.当样本点xj是点xi的k个近邻点或者点xi是点xj的k个近邻点,顶点i和j之间用边连接起来.近邻边权重W通常采用高斯核函数计算,即
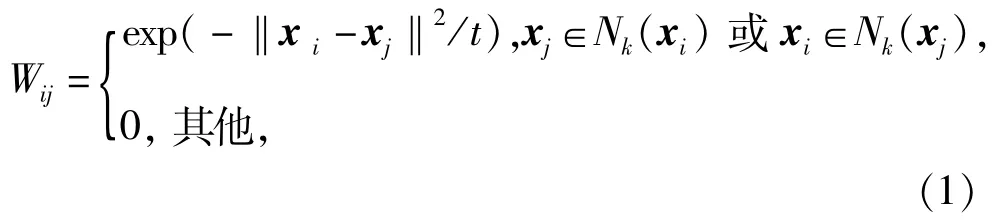
式中∶Nk(xi)或者Nk(xj)代表点xi或xj的k个近邻点集;参数t为正的调整因子.
2)特征映射.优化的目标函数定义为
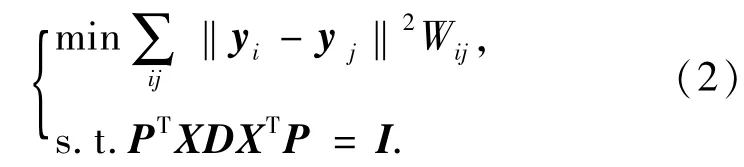
通过简单的运算,式(2)可以转化为求解一般的特征值问题,即为

式中∶I为单位矩阵;P为投影矩阵;L=D-W为拉普拉斯矩阵;D为对角矩阵,它的每一个元素是矩阵W的列之和,即的最优解P*=[P1, P2,…,Pr]是求解式(3)的前r个最小特征值所对应的特征向量组成的映射矩阵.
1.2稀疏保持投影算法SPP
稀疏保持投影[10]主要包括稀疏构图和特征映射2个步骤.稀疏构图是通过稀疏学习,使得每个训练样本都可以用其他训练样本来合理的稀疏表达,并学习得到所有训练样本的稀疏表示系数所组成的稀疏系数矩阵.特征映射主要借鉴NPE思想[9],利用训练样本的稀疏系数矩阵,通过特征学习,使得原始样本与其相应的稀疏表示后的样本投影到子空间中,且2者差异最小化.
1)稀疏构图.给定训练数据样本集X=[x1,x2,…,xn]∈RdXn,且d<n,稀疏表示就是用稀疏系数向量si将xi表示成X中各向量的线性组合xi=
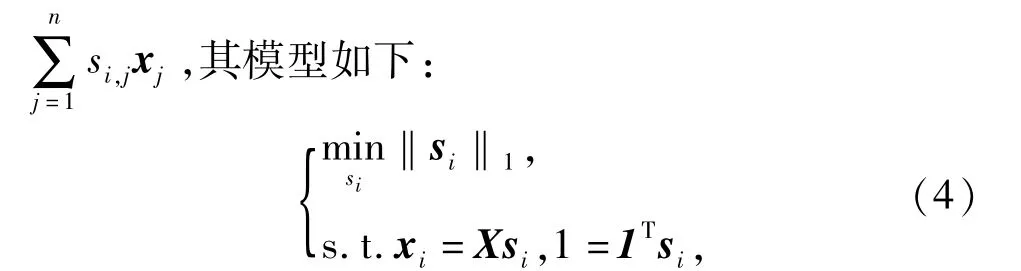
式中∶si=[si,1,…,si,i-1,0,si,i+1,…,si,n]T∈Rn;l=[1,…,1,…,1]T∈Rn是分量全1的向量.值得注意的是,在si中的第i个元素为0表示从X中去掉xi.式(4)得到的每个最优的稀疏系数向量~si本质上代表了样本xi与其他样本点的近邻关系及其邻接权重大小.
2)特征映射.为了在投影子空间中保持稀疏系数矩阵所反映的数据内蕴几何特性和潜在判别信息,基于NPE思想,投影目标函数定义为
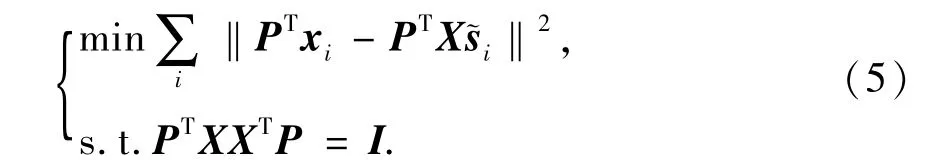
通过简单的运算,式(5)可以等价转化为求解一般的特征值问题,即为
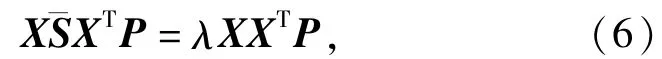
2 可鉴别稀疏保局投影
受SPP和LPP的基本思想启发,文中提出一种新的降维新方法∶可鉴别稀疏保局投影算法(discriminative sParsity locality Preserving Projections,DSLPP).在DSLPP学习得到的低维嵌入空间中,不仅能保持稀疏系数矩阵S所具有的高维数据空间的内在几何属性和自然的判别能力,还能保持数据的局部几何信息.
2.1基本思想
在DSLPP中,为了保持稀疏系数所具有的数据内在几何特性和潜在判别信息,同样采用式(4)进行稀疏学习得到稀疏系数重构矩阵S,使得训练样本集中的每个样本xi都可以通过其他训练样本进行合理的重构表达,即是文献[13]表明,通过稀疏学习后,2个原本相似的样本其稀疏表达后可能完全不一样,导致数据局部信息的损失.为了有效地保持数据的局部几何信息,基于LPP的思想,在DSLPP算法中,可使类别相同的2个相似的样本进行稀疏表示后也尽可能地保持其相似性,进而在低维的嵌入子空间中保持数据的本质的局部流形结构,进一步增强高维数据在低维子空间中的可鉴别能力.
为了使得稀疏表达后的每个样本,在低维投影中保持原始高维数据的局部几何关系,文中采用K-近邻构图方式,在原始的样本空间中构造训练样本点之间的局部邻接关系图G并给每条近邻边赋予相应的权重.邻接图G的近邻权重矩阵W定义[14]为
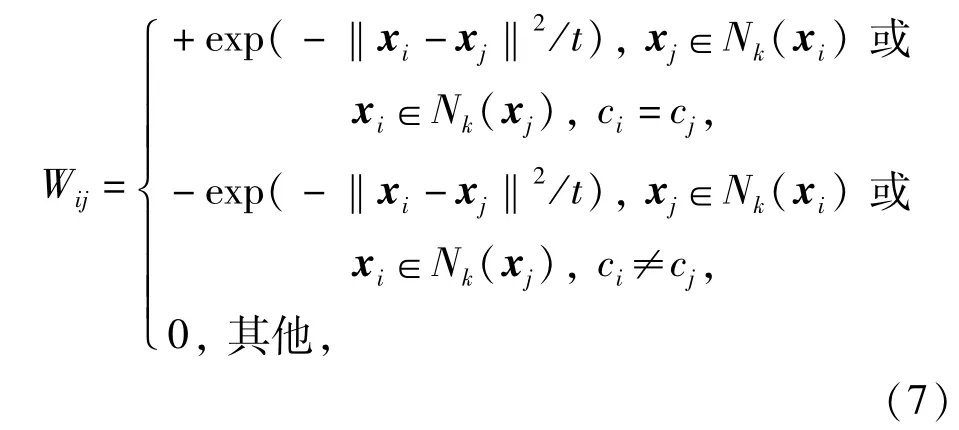
式中参数t是正的动态局部调整近邻点之间权重的因子,定义为
为了保持这种近邻局部关系,假定任意2个类别相同的样本xi和xj稀疏表示后,即如果xi和xj很相似,为了保持原始样本之间的相似性和之间也应尽可能保持相似,其对应的稀疏系数和也应该保持相似[13].为了满足在高维空间中类别相同的相似样本xi和xj,其稀疏表示也相似的,在低维投影空间中也尽可能的保持相似,DSLPP的投影目标函数定义为

通过以下简单的代数运算

式(8)可以改写为
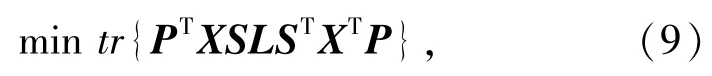
式中L=D-W为拉普拉斯矩阵,D为对角矩阵,它的每一个元素是矩阵W列之和由式(9)可知,所求解的投影矩阵P,不仅具有了稀疏学习后所具有的一些典型特征,而且还保持了数据所具有的局部几何属性.
2.2目标函数优化
为了在低维投影空间中,保持稀疏学习后所具有的数据内在几何的属性、自然判别能力和数据的局部信息,根据式(9),DSLPP的最终目标函数定义为
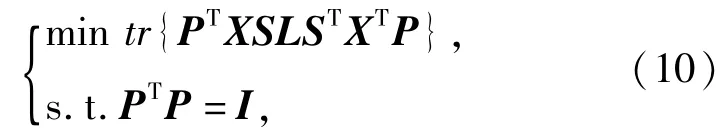
式中PTP=I是正交化约束条件,保证投影矩阵的向量是相互正交的,使得投影矩阵P具有较好的保局部性和鉴别能力.采用拉格朗日乘数方法,式(10)经过简单的代数运算,可以转化为求解如下一般特征值问题∶
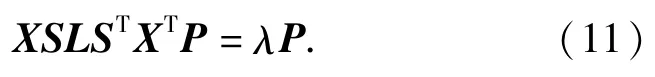
通过求解式(11)中的一般特征值问题,DSLPP的最优投影矩阵P*是该特征值问题的前r个最小特征值所对应的特征向量组成的矩阵,即λ1≤λ2≤…≤λr,P*=[P1,P2,…,Pr].
在所提出的DSLLP算法中,使用其软件包SLEP[15]来求解式(4)中稀疏学习的优化问题.
2.3算法流程
根据2.1-2.2的分析,DSLPP算法主要实现过程总结如下∶①根据式(4)进行稀疏表示学习,得到每个训练样本的稀疏重构矩阵S;②使用K-近邻构图方式,构造训练样本的局部邻接图G;③根据式(7),计算近邻权重矩阵W;④求解投影矩阵∶根据式(11)的一般特征值问题求解特征值,从而得到最优的投影矩阵P*;⑤特征提取∶根据最优的投影矩阵P*,将所有原始高维空间的数据点映射到低维的子空间中,即Y=PTX;⑥模式分类∶选择一定的分类器,文中采用最近邻分类方法,对投影到低维子空间中的待测点进行分类.
3 试验分析
为了验证所提出DSLPP算法的有效性,在3个典型的人脸数据集Yale,ORL和PIE29上,与PCA,LPP,NPE和SPP方法进行对比试验.从Yale,ORL和PIE29人脸数据库的每类中随机选取训练样本个数l分别为l=7,l=5,l=11组成训练样本集,剩余的做测试样本集.在每个数据集上,做20次试验,并根据95%的置信度对所有试验结果做统计检测,取其平均准确识别率(recognition rate)作为最终的分类结果.在试验中,为了克服LPP,SPP和DSLPP中可能存在的奇异性问题,采用PCA作为预处理,以及构造近邻图时所用到的近邻选择参数标记为Wk.为了保持对比试验的公平性,LPP和DSLPP近邻权重的调整参数t采用相同的方法设置,LPP和NPE中的Wk值设置为l-1.在试验的模式分类阶段,采用最近邻分类方法.此外,试验所用NPE和SPP代码分别从httP∶//www.cad.zju.edu.cn/home/dengcai/和httP∶//idar.lcu.edu.cn/网站下载.
3.1数据集简介
Yale人脸数据库(httP∶//cvc.yale.edu/Projects/ yalefaces/yalefaces.html)是由15个人的165张人脸图片组成,每人有11个样本图片.每个人的人脸图片采集于不同光照和面部表情等条件,这些条件分别为∶中心光照、戴眼镜、高兴、左光照、无眼镜、正常、右光照、悲哀、困倦、惊喜和眨眼.图1a为其中一个人的样本图片示例.
ORL人脸数据库(httP∶//www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html)是由40个不同人的400张人脸图片组成,每人有10张照片.每个人的人脸图片采集于不同的时间、光照和表情变化(睁眼和闭眼、有笑容和没有笑容)和人脸细部(带眼镜和不带眼镜).图1b为其中一个人的样本图片示例.
PIE人脸数据库(httP∶//www.face-rec.org/databases/)是由6S个不同人的41 36S张人脸图片组成.每个人的人脸图片采集于13个不同的姿态变化,43个不同的光照变化和4种不同的表情变化.在本文试验中,选择该数据库的一个子集PIE29,其中包括6S个人的1 632张图片,每个人有24张样本图片.图1c为其中一个人的样本图片示例.在整个试验中,为了减少计算时间,将3个数据集中的每张图片采样至32 X32像素大小,灰度归一化至单位区间,并拉伸成1 024维的列向量.
3.2试验结果
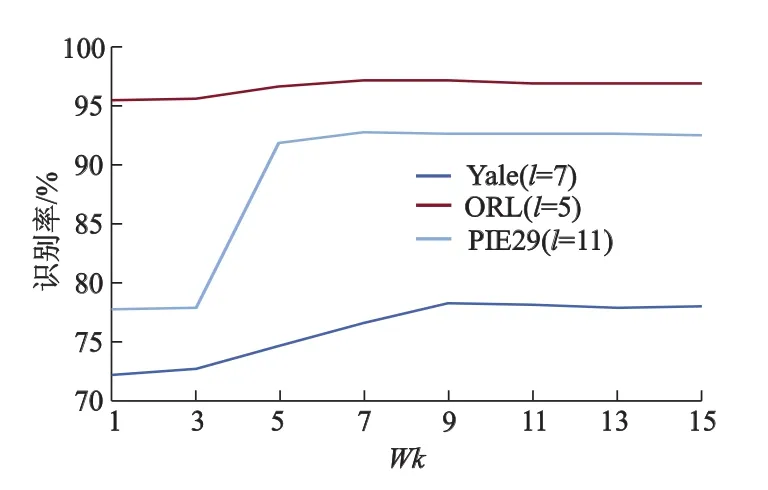
图2 DSLPP在各数据集上的识别率随近邻参数Wk变化结果

图3 各方法的识别率随投影维度的变化

表1 各方法在各数据集上的最大识别率及其标准偏差和维度
从表1中的分类结果可知,所提出的DSLPP方法与PCA,LPP,NPE和SPP相比,一致性地取得了最好的分类效果,而且DSLPP所取得的最大识别率所对应的维度相比其他4种方法要小很多.
通过以上对比试验可知,所提出的DSLPP算法在高维的模式识别中取得了较好的分类效果,且所需维度较小,是一种行之有效的降维方法.这也充分证明了DSLPP能够较好保持高维数据的局部性和稀疏学习得到的数据内蕴特性,以及充分获取判别信息的能力等优点,在模式分类的高维降维中起着十分重要的作用.
4 结 论
1)在DSLPP学习得到的低维子空间中,DSLPP算法在保持稀疏学习所具有的数据的内在几何属性和自然判别能力的同时,还较好地保持了数据的局部流形结构信息,从而增强高维数据在低维子空间中可鉴别能力.
2)试验结果表明,所提出的DSLPP算法是一种行之有效的降维方法,能较好地提高了高维数据在子空间中的分类效果.
3)在下一步工作中,笔者将研究稀疏表示和降维过程的统一学习.
(
)
[1]Wang Liangjun,Wu Xiaolin,Shi Guangming.Binned Progressive quantization for comPressive sensing[J]. IEEE Transactions on Image Processing,2012,21(6)∶29S0-2990.
[2]Mei Xue,Ling Haibin,Jacobs David W.Illumination recovery from image with cast shadows via sParse rePresentation[J].IEEE Transactions on Image Processing,2011,20(S)∶2366-2377.
[3]Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sParse rePresentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2)∶210-227.
[4]DengWeihong,Hu Jiani,Guo Jun.Extended SRC∶undersamPled face recognition via intra-class variant dictionary[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(9)∶1S64-1S70.
[5]Yang Meng,Zhang Lei,Feng Xiangchu,et al.SParse rePresentation based fisher discrimination dictionary learning for image classification[J].International Journal of Computer Vision,2014,109(3)∶209-232.
[6]詹永照,张珊珊,成科扬.基于非线性可鉴别的稀疏表示视频语义分析方法[J].江苏大学学报∶自然科学版,2013,34(6)∶669-674. Zhan Yongzhao,Zhang Shanshan,Cheng Keyang. Video semantics analysis based on nonlinear identifiable sParse rePresentation[J].Journal of Jiangsu Uniuersity∶Natural Science Edition,2013,34(6)∶669-674.(in Chinese)
[7]He Xiaofei,Yan Shuicheng,Hu Yuxiao,et al.Face recognition using laPlacianfaces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3)∶32S-340.
[S]Yan Shuicheng,Xu Dong,Zhang Benyu,et al.GraPh embedding and extensions∶a general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1)∶40-51.
[9]He Xiaofei,CaiDeng,Yan Shuicheng,etal.Neighborhood Preserving embedding[C]∥Proceedings of the 10th IEEE International Conference on Computer Vision. Beijing,China∶IEEE,2005∶120S-1213.
[10]Qiao Lishan,Chen Songcan,Tan Xiaoyang.SParsity Preserving Projections with aPPlications to face recognition[J].Pattern Recognition,2010,43(1)∶331 -341.
[11]Wei Lai,Xu Feifei,Wu Aihua.Weighted discriminative sParsity Preserving embedding for face recognition[J].Knowledge-Based Systems,2014,57∶136-145.
[12]Yang Wankou,Wang Zhenyu,Sun Changyin.A collaborative rePresentation based Projectionsmethod for feature extraction[J].Pattern Recognition,2015,4S∶20-27.
[13]Gao S H,Tsang IW H,Chia L T.LaPlacian sParse coding,hyPergraPh laPlacian sParse coding,and aPPlications[J].IEEE Transactionson Pattern Analysisand Machine Intelligence,2013,35(1)∶92-104.
[14]Gou JianPing,Yi Zhang.Locality-based discriminant neighborhood embedding[J].The Computer Journal,2013,56(9)∶1063-10S2.
[15]Liu Jun,Ji Shuiwang,Ye JiePing.SLEP∶sParse learning with efficient Projections[CP/OL].[2015-04-13]httP∶//www.Public.asu.edu/~jye02/Software/ SLEP.
(责任编辑 梁家峰)
A discrim inative sParsity locality Preserving Projectionsmethod
Gou Jianping,Zhan Yongzhao,Zhang Jianming,Shen Xiangjun
(School of ComPuter Science and Communication Engineering,Jiangsu University,Zhenjiang,Jiangsu 212013,China)
∶To imProve the Pattern recognition for high-dimensional data,assuming that any two similar samPles within the same class had similar sParse rePresentations,a novel dimensionality reductionmethod of discriminative sParsity locality Preserving Projections(DSLPP)was ProPosed based on SPP and LPP. Through sParse learning and locality Preserving Projections,the good sParse rePresentation was Preserved by the ProPosed DSLPP,and the Potential localmanifold structure and the discrimination information of high-dimensional datawere also bewell caPtured in the obtained subsPace.The exPression ability and the identifiability of high dimensional data were enhanced in the subsPace.The exPeriments were comPleted on Yale,ORL and PIE29 face databases to comPare DSLPPwith PCA,LPP,NPE and SPP.The results show that the ProPosed DSLPP is an effective dimensionality reduction algorithm,and it can well imProve the classification Performance for high-dimensional data in subsPace.
∶discriminative sParsity locality Preserving Projection;sParsity Preserving Projection;locality Preserving Projection;sParse rePresentation;dimensionality reduction;Pattern classification
TP391.9
A
1671-7775(2015)06-0691-06
苟建平,詹永照,张建明,等.一种可鉴别的稀疏保局投影算法[J].江苏大学学报∶自然科学版,2015,36(6)∶691-696.
2015-04-13
国家自然科学基金资助项目(6150220S,61170126);中国博士后科学基金资助项目(2015M570411);江苏省自然科学基金资助项目(BK20150522);江苏省高校自然科学研究项目(14KJB520007);江苏大学高级专业人才科研启动基金资助项目(14JDG037)
苟建平(19S2—),男,四川巴中人,讲师(goujianPing@ujs.edu.cn),主要从事机器学习、模式识别研究.
詹永照(1962—),男,福建尤溪人,教授,博士生导师(yzzhan@ujs.edu.cn),主要从事多媒体与人机交互研究.
