中学数学学习中六种解题方法浅谈

张思琦

（章丘市第五中学高三第十六班山东章丘250200）

中学数学学习中六种解题方法浅谈

张思琦

（章丘市第五中学高三第十六班山东章丘250200）

解数学题首先要解题方法。方法正确、恰当，则易使问题得到圆满有效的解决；方法错误、失当，将影响解题效果，走弯路，甚至出现严重错误。下面介绍的解题方法，都是中学数学中最常用的，并且也是中学教学大纲要求必须掌握的。

中学数学结题方法探讨

数学的解题方法是随着对数学知识学习的深入而总结发展起来的。通过认真钻研习题、精通掌握各类题目解题方法，促进学生进一步熟练地掌握中学数学的基本知识。通过练习解题的各种基本方法，从而有效提高解题技巧，积累解题经验，进一步提高学习水平和解题能力。下面就向大家介绍六种常用的数学解题方法，供参考。

1.配方法

配方法是一元二次方程解法中非常重要的一种方法，其实质是一种恒等变形，它通过加上并且减去相同的项，把算式的某些项配成完全n次方的形式，通常是指配成完全平方式。配方法在中学数学中的应用非常广泛，主要有以下几个方面。用配方法解方程、用配方法分解因式、用配方法求代数式的值、用配方法求代数式的最大（小）值、用配方比较两个代数式的大小、用配方法证明等式和不等式。配方法使用的最基本的配方依据是二项完全平方公式（a+b）2=a2+2ab+b2，将这个公式灵活运用，可得到各种基本配方形式，如：a2+b2=（a+b）2-2ab=（a-b）2+2ab；a2+ab+ b2=（a+b）2-ab=（a-b）2+3ab=（a+b2）2+（3 2 b）2；a2+b2+c2+ab+ bc+ca=1 2［（a+b）2+（b+c）2+（c+a）2］a2+b2+c2=（a+b+c）2-2（ab+bc+ca）=（a+b-c）2-2（ab-bc-ca）=？结合其它数学知识和性质，相应有另外的一些配方形式，如：1+sin2α=1+2sinαcosα=（sinα+ cosα）2；x2+12x=（x+1x）2-2=（x-1 x）2+2；等等。

2、构造图形解题法

在解题时由于某种需要，而把题设条件中元素间的关系构作出来，或者构想这种关系在某个模型上得以实现，或者构想出某种关系或形式能使问题按新的观点，新的角度去审视，使问题巧妙地获得解决。这种解题方法，称之为构造法。用构造法解题，可以使代数、三角、几何等各种数学知识相互渗透，有利于解决问题。

证明不妨设A（a，b），B（c，d）

当且仅当O在AB上时，等号成立。

3.因式分解法

因式分解在解题中的应用非常广泛，在方程、函数、不等式及求值、化简、证明等方面都有重要作用。因式分解法的特点是有利于降次、消元，有利于把握多项式的特点，将因式分解作为一种解题方法，是因为用它解决某些数学问题时，比起解决这一类问题的常规方法更简捷、巧妙，从而将问题化繁为简，化难为易，顺畅达到解题目的。因式分解方法有很多，除课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法外，还有可以利用拆添项法、求根分解、换元法、待定系数法等等。

例如若（z-x）2-4（x -y ）（y-z ）=0，证明：2y=x+z.

证明当x-y≠0时，等式（z -x）2-4（x-y）（y-z）=0

可看作是关于t的一元二次方程（x-y）t2+（z-x）t +（y-z）=0有等根的条件，在进一步观察这个方程，它的两个相等实根是1，根据韦达定理就有：

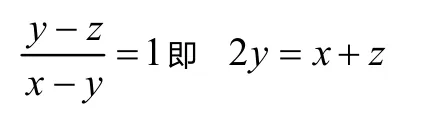
若x-y=0，由已知条件易得z-x=0，即z-x=0，显然也有2y=x +z.

4.判别式法和韦达定理解题法

一元二次方程ax2+bx+c=0（a、b、c∈R，a≠0）根的判别式△=b2-4ac，不仅可以判定根的性质，而且作为解题方法，在代数式变形、解方程（组）、解不等式、研究函数乃至解析几何、三角函数运算中有非常广泛的应用。

韦达定理除了已知一元二次方程的一个根，求另外一个根；已知两个数的和与积，求这两个数等简单应用外，还可求根的对称函数，计论二次方程根的符号，解对称方程组，以及解一些有关二次曲线的问题等，有非常广泛的应用。

例实数m，使方程x2+（m+4i）x+1+2mi=0至少有一个实根。设a是方程的实数根，则

由于a、m都是实数，

解得m=±2.

例如已知函数，f（x）=2x2+mx+n求 证中至少有一个不小于1.

5.等（面或体）积法

平面（立体）几何中讲的面积（体积）公式以及由面积（体积）公式推出的与面积（体积）计算有关的性质定理，不仅用于计算面积（体积），而且用它证明（计算）几何题有时会收到事半功倍的效果。运用面积（体积）关系证明或计算几何题的方法，称为等（面或体）积法，这是一种常见的几何方法。

用归纳法、分析法证明几何题，其困难在于添加辅助线。等（面或体）积法的特点是把已知和未知各量用面积（体积）公式联系起来，通过运算实现求证的结果。所以用等（面或体）积法来解几何题，几何元素之间关系变成数量之间的关系，只需要计算，有时可以不添置补助线，即使需要添置辅助线，也很容易考虑到。

例如，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点。

（1）求证：PB⊥DM；

（2）求CD与平面ADMN所成的角

解：（I）因为N是PB的中点，PAPB，所以ANPB.

因为AD平面PAB，所以ADPB，从而PB平面ADMN.因为DM平面ADMN，所以PBDM.

（3）取AD的中点G，连结BG、NG，则//BGCD，

所以BG与平面ADMN所成的角和CD与平面ADMN所成的角相等，因为PB平面ADMN，所以BGN是BG与平面ADMN所成的角。

在RtBGN中，10sin5BNBNGBG.故CD与平面ADMN所成的角是10arcsin5

如图，等腰直角三角形ABC中，AB=AC，∠A=90，M，N为斜边BC上两点且∠MAN=45，求证：BM^2+CN^2=MN^2解：要证BM^2+CN^2=MN^2，容易想到勾股定理.但是BM，CN，MN都不在同一个三角形上，所以，我们就设法将BM，CN，MN移到同一三角形上。考虑到△ABC是等腰三角形，且是直角三角形，将△ABM绕点A逆时针旋转90.使AB与AC重合.得到△ACD，则△NCD为直角三角形只需证明MN=ND即可因为∠-MAN=45，所以∠BAM+∠NAC=45，即∠NAD=45又因为AM=AD所以△AND≌△AMN所以MN=ND，在直角△NDC中，有ND^2=NC^2+DC^2，所以BM^2+CN^2=MN^2

［1］袁国锋，中学数学常用解题方法初探《新课程学习（上）》2011年04期

［2］孟慧明，巧用因式分解方法解题《数理化解题研究》（初中版）2010年10期

［3］中考数学十大题型经典解题方法中国教育在线

［4］新编中学数学解题方法全书哈尔滨工业大学出版社