一种火箭助飞鱼雷命中概率实时评估模型

丁光强（海军装备部驻上海地区军事代表局，上海200129）



一种火箭助飞鱼雷命中概率实时评估模型

丁光强
（海军装备部驻上海地区军事代表局，上海200129）

摘要：火箭助飞鱼雷命中概率实时评估结果是指挥决策的重要依据。首先，根据每个节点相对目标距离舷角的不同，构建火箭助飞鱼雷的静态命中概率表；其次，对火箭助飞鱼雷的射击误差区域进行分区，计算每个射击误差子区域对应的入水点落入概率；再次，根据每个射击误差子区域端点相对目标的距离和舷角，调用静态命中概率表计算每个子区域对应的平均命中概率；最后，将每个射击误差子区域的落入概率与该子区域对应的平均命中概率的乘积进行求和，得到火箭助飞鱼雷的实时命中概率。

关键词：火箭助飞鱼雷；命中概率；实时评估；射击误差；静态命中概率表

火箭助飞鱼雷命中概率是作战指挥决策的重要依据。及时准确地评估火箭助飞鱼雷的命中概率，将为指挥决策提供重要参考。理论上，在射击条件一定的情况下，通过蒙特卡洛法仿真可以获得火箭助飞鱼雷的命中概率[1-2]，但此方法难以满足作战指挥决策实时性的要求。因此，建立火箭助飞鱼雷命中概率的实时评估模型是十分必要的。本文探讨一种基于静态命中概率表的火箭助飞鱼雷命中概率实时评估模型。

1　火箭助飞鱼雷静态命中概率表的构建

1.1静态命中概率表的构建

在其他条件相同的情况下，火箭助飞鱼雷的命中概率只和入水点相对目标的距离和舷角有关[3]。对于某一次射击而言，假设火箭助飞鱼雷在某一点入水，只要已知该入水点相对目标的距离和舷角，即可由蒙特卡洛法仿真得到对应的命中概率[4-7]。因此，可以对火箭助飞鱼雷可能的入水区域进行分区，根据蒙特卡洛法仿真计算每个区域端点（入水点）对应的命中概率。这些端点对应的命中概率构成火箭助飞鱼雷的静态命中概率表[8]。

图1以火箭助飞鱼雷入水时刻的目标位置点为坐标原点、以目标航向为正方向建立极坐标。

将坐标系按方位M等分，按距离N等分（每一环间距为Δd）得M×N个子区域，M=32，N=10。Pti_j为第i方位、第j环所对应的点，Di_j为第i方位、第j环所对应的入水区域。A点记为Pt6_8（i=6, j=8），阴影区记为D6_8。

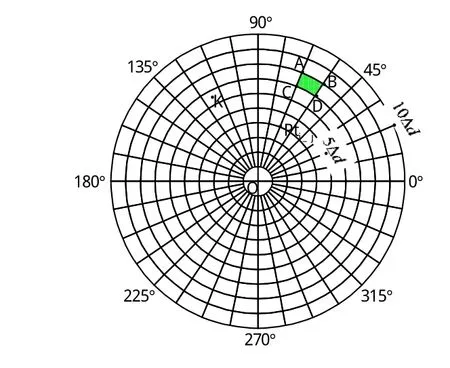
图1　目标周围分区Fig.1 Area partitioned off around the target

A点相对目标的距离DA、舷角Qm_A分别为：

由A点相对目标的距离舷角（DA、Qm_A）可仿真得到火箭助飞鱼雷在A点入水时的命中概率P6_8。同理，对任意一入水点Pti_j，均可求得其对应的命中概率Pi_j。获得任意一点Pti_j对应的命中概率Pi_j后，即可得到火箭助飞鱼雷的静态命中概率表见表1。

表1　火箭助飞鱼雷静态命中概率表Tab.1 Static hit probabilitsheet of RAT

表1　火箭助飞鱼雷静态命中概率表Tab.1 Static hit probabilitsheet of RAT

j　12⋮M i 1 P1_1 P2_1⋮PM_12 P1_2 P2_2⋮PM_2………⋮…N P1_N P2_N⋮PM_N

1.2任意入水点命中概率的求解

假设火箭助飞鱼雷入水点落在任意区域Di_j内时对应的平均命中概率为PDi_j。为简化计算，令PDi_j等于区域Di_j端点对应的命中概率的算术平均值，即：式中，Pi_j、Pi-1_j、Pi_j-1、Pi-1_j-1分别为区域Di_j的4个端点对应的命中概率，由静态命中概率表直接查到。

例如，火箭助飞鱼雷入水点落在区域D6_8内对应的平均命中概率PD6_8为

对于任意一入水点K，若K∈Di_j，则令该入水点对应的命中概率等于区域平均命中概率PDi_j，即

因此，根据静态命中概率表可以求得任意一个入水点对应的命中概率。

2　火箭助飞鱼雷命中概率实时评估模型

2.1射击误差子区域的坠入概率

根据射击误差理论，火箭助飞鱼雷射击误差服从以射击瞄准点为中心的二维正态分布[9]。令σ、σ分别为火箭助飞鱼雷射击误差的纵向分量和侧向分量。根据误差理论可知，火箭助飞鱼雷入水点落在-4σ≤≤4σ、-4σ≤≤4σ范围内的概率为99.99%[10]，即火箭助飞鱼雷入水点几乎全部落在4倍的射击误差范围内。

以射击误差点O(-4σ,-4σ)为坐标原点，以火箭助飞鱼雷射击方向为轴正方向，根据右手法则建立直角坐标系，如图2所示。将入水点射击误差区域进行2m等分，共可得4m2个矩形子区域。图2中，m=4，每个矩形区域的长度、宽度分别为σ、σ，Z(4σ,4σ)点为射击散布中心。火箭助飞鱼雷射击误差的分布密度可写为

图2　射击误差区域划分Fig.2 Partition zone of the fire error distribution

以Si_j表示轴第i个刻度、轴第j个刻度所对应的射击误差子区域（i、j分别对应该区域右上角顶点的刻度）。例如，图2中阴影区记为S7_6。对于任意一个子区域Si_j，坐标取值范围为(i-1)σ≤≤iσ，(j-1)σ≤≤jσ。因此，火箭助飞鱼雷入水点落在区域Si_j内的概率PSi_j为

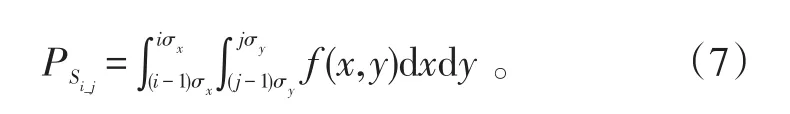
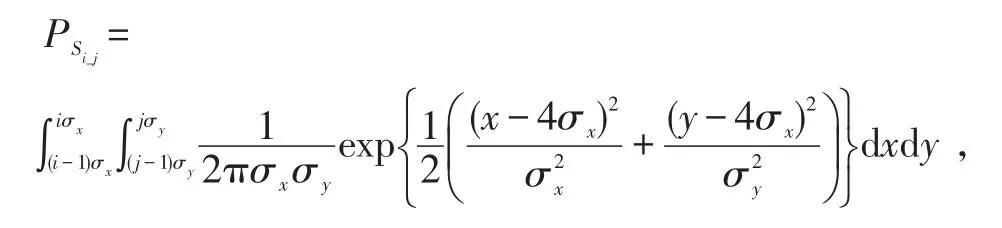
式（6）代入式（7）可得称PSi_j为子区域Si_j对应的坠入概率。只要给定i、j的值，即可求得PSi_j的值。

2.2射击误差子区域的平均命中概率

如图3所示，以火箭助飞鱼雷入水点散布中心为O原点，以射击方向为轴，与射击方向相垂直的方向为轴建立坐标系。火箭助飞鱼雷入水时刻目标预计达到O′点，目标航向为Cm。

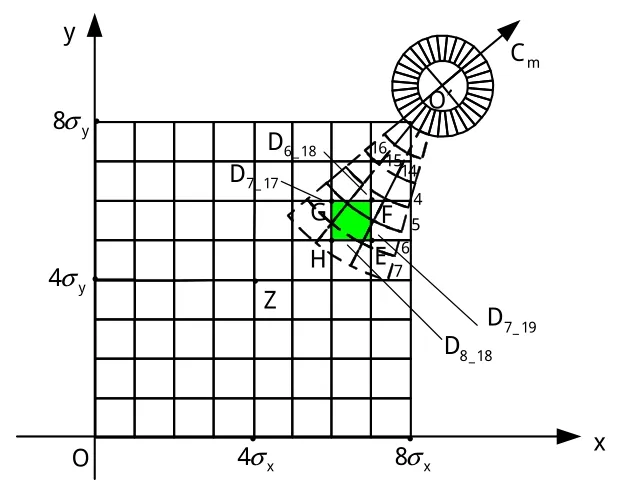
图3　子区域平均命中概率解算Fig.3 Sub-zone average hit probabilitcalculation

以区域S7_6为例，E、F、G、H分别为射击误差区域S7_6的4个顶点。则有：E∈D7_19，F∈D6_18，G∈D7_17，H∈D8_18。因此，入水点E、F、G、H对应的命中概率分别为：PE=PD7_19

，PF=PD6_18

，PG=PD7_17

，

PH=PD6_18

。其中，PD7_19

、PD6_18

、PD7_17

和PD6_18可由静态命中概率表求得。因此，火箭助飞鱼雷入水点落在散布区域S7_6内时对应的平均命中概率为称PˉS为射击误差子区域S7_6的平均命中概率。对于

7_6任意子区域Si_j，均可采用以上方法求得对应的平均命中概率PˉS。

i_j

根据全概率公式，火箭助飞鱼雷命中概率P等于每个射击误差子区域Si_j对应的坠入概率PSi_j与平均命中概率PˉSi_j的乘积之和[10]，即：式中，m表示4σ误差区域的等分数。

3　实例计算

某时刻，本舰位于W点，本舰航向CW=90°，航速VW=15 kn，测得目标航向Cm=120°，航速VW=6 kn，距离Dm=16.7km，M′为火箭助飞鱼雷射击瞄准点。

以火箭助飞鱼雷射击瞄准点M′为坐标原点，以目标航向Cm为轴正方向，根据右手规则建立坐标系如图4所示。

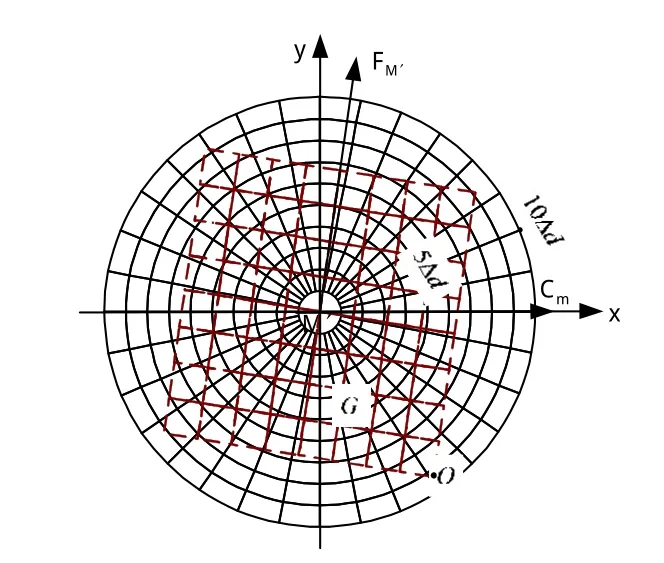
图4　命中概率实例评估Fig.4 An eample to evaluate RAT’s hit probabilit

图4中，FM′方向为火箭助飞鱼雷射击正方向，虚线所示矩形区域为目标射击散布区域。根据射击误差模型和区域划分方法，每个矩形子区域端点相对M′的距离和舷角均可计算得到。

假设火箭助飞鱼雷射击误差纵向分量σ=500 m，侧向分量σ=600 m。按照图2方法划分射击误差区域，可求得火箭助飞鱼雷入水点落在每个区域内的概率如表2所示。

参照美军阿斯洛克火箭助飞鱼雷的性能，可仿真得到火箭助飞鱼雷的静态命中概率表。根据静态命中概率表，可计算得到火箭助飞鱼雷射击散布区域端点对应的命中概率如表3所示。

由表3计算得到射击误差子区域Si_j对应的平均命中概率PˉSi_j如表4所示。

表2　射击误差子区域的坠入概率Tab.2 Dropping probabilitfor each sub-zone　×10-4

表2　射击误差子区域的坠入概率Tab.2 Dropping probabilitfor each sub-zone　×10-4

j　12345678 i 10 0.3 1.7 55 1.7 0.3 0 20 4.5 29.1 73 73 29.1 4.5 0 322 9 185 464 464 185 29 2 447 3 464 1 165 1 165 464 73 4 547 3 464 1 165 1 165 464 73 4 622 9 185 464 464 185 29 2 70 4.5 29.1 73 73 29.1 4.5 0 80 0.3 1.7 55 1.7 0.3 0

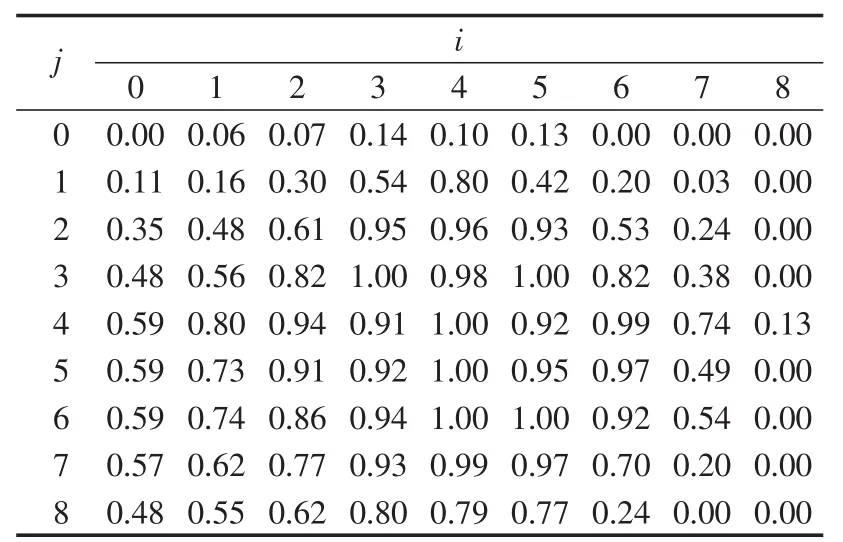
表3　射击误差子区域端点对应的命中概率Tab.3 Hit probabilities for each sub-zone’s nodes

表4　射击误差子区域的平均命中概率Tab.4 Average hit probabilitfor each sub-zone

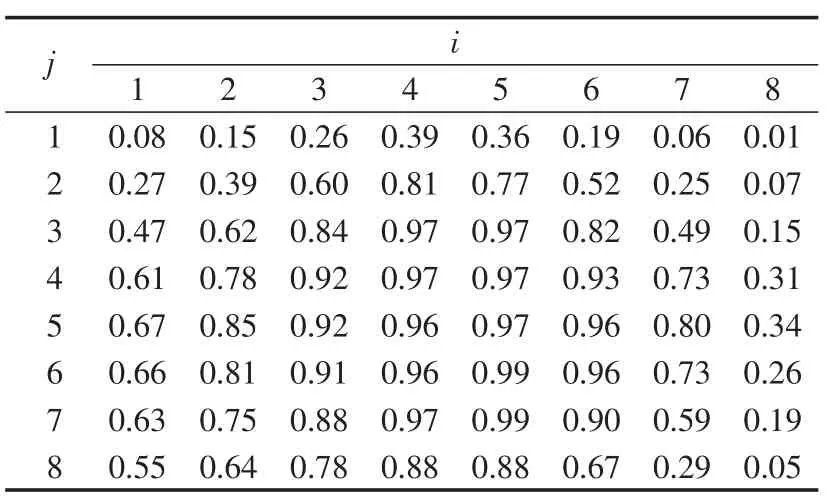
表4　射击误差子区域的平均命中概率Tab.4 Average hit probabilitfor each sub-zone

j　12345678 i 1 0.08 0.27 0.47 0.61 0.67 0.66 0.63 0.55 2 0.15 0.39 0.62 0.78 0.85 0.81 0.75 0.64 3 0.26 0.60 0.84 0.92 0.92 0.91 0.88 0.78 4 0.39 0.81 0.97 0.97 0.96 0.96 0.97 0.88 5 0.36 0.77 0.97 0.97 0.97 0.99 0.99 0.88 6 0.19 0.52 0.82 0.93 0.96 0.96 0.90 0.67 7 0.06 0.25 0.49 0.73 0.80 0.73 0.59 0.29 8 0.01 0.07 0.15 0.31 0.34 0.26 0.19 0.05

根据表2及表4计算结果，火箭助飞鱼雷命中概率P为即火箭助飞鱼雷在当前战场态势下的射击命中概率实时评估值为0.938。

4　结束语

火箭助飞鱼雷的命中概率直接影响指挥员的作战指挥决策。本文基于静态命中概率表建立了基于火箭助飞鱼雷命中概率实时评估模型。该评估模型是以火箭助飞鱼雷在任意入水点的命中概率已知为前提的。火箭助飞鱼雷在任意入水点的命中概率需要结合鱼雷性能、水声环境以及目标规避机动假设等进行进一步的深入研究。

参考文献：

[1]邵伟.蒙特卡洛方法及在一些统计模型中的应用[D].济南：山东大学，2012：1-8. SHAO WEI. Monte carlo methods and their applications in some statistical model[D]. Jinan：Shandong Universit，2012：1-8.（in Chinese）

[2]孟庆玉，张静远，宋保维.鱼雷作战效能分析[M].北京：国防工业出版社，2003：127-161. MENG QINGU，ZHANG JINGUAN，SONG BAOWEI. Analsis of operational Effectiveness for torpedo [M]. Beijing：National Defense IndustrPress，2003：127-161.（in Chinese）

[3]周明，徐德民，刘影，等.溅落点散布误差对火箭助飞鱼雷射击效率影响研究[J].系统工程理论与实践，2007 （9）：153-158. ZHOU MING，U DEMIN，LIUING，et al. Infection of impact dispersion to the rocket assisted torpedo fire efficienc[J]. Sstems Engineering-Theor& Practice，2007 （9）：153-158.（in Chinese）

[4]王晓娟，唐世轩，刘正平.火箭助飞鱼雷系统建模与空中弹道仿真研究[J].弹箭与制导学报，2003，23（2）：51-55. WANGIAOJUAN，TANG SHIUAN，LIU ZHENGPING. The rocket-assisted torpedo sstem to set up the mold and air the trajectorto imitate the true research[J]. Journal of Projectiles. Rockets. Missiles and Guidance，2003，23（2）：51-55.（in Chinese）

[5]薛晓中，邵大燮，金友兵.火箭助飞鱼雷的弹道分析[J].兵工学报，2001，22（4）：452-455.UEIAOZHONG，SHAO DAIE，JINOUBING. Ballistic characteristics of rocket assisted torpedo[J]. Acta Armamentarii，2001，22（4）：452-455.（in Chinese）

[6]寇祝，周明.基于超视距通道的火箭助飞鱼雷射击效率研究[J].鱼雷技术，2009，17（2）：57-60. KOU ZHU，ZHOU MING. Studon fire efficiencof rocket- assisted torpedo based on over- the- horizon fire Channel[J]. Torpedo Technolog，2009，17（2）：57- 60. （in Chinese）

[7]赵学涛，贾跃，林贤杰.舰载直升机引导火箭助飞鱼雷攻潜效能模型与仿真[J].鱼雷技术，2009，17（1）：60-63. ZHAOUETAO，JIAUE，LINIANJIE. Anti-submarine operational effectiveness model and simulation of rocket- assisted torpedo guided bshipboard helicopter [J]. Torpedo Technolog，2009，17（1）：60-63.（in Chinese）

[8]STEPHEN M VALERIO. Probabilitof kill for vla asroc torpedo launch[D]. Montere：Naval Postgraduate School，2009.

[9]王炳魁，门金柱，周明.火箭助飞鱼雷入水点散布误差综合分析[J].舰船科学技术，2009，31（11）：59-62. WANG BINGKUI，MEN JINZHU，ZHOU MING. General studon falling dispersion error of rocket-assisted torpedo[J]. Ship Science & Technolog，2009，31（11）：59-62.（in Chinese）

[10]殷凤，王鹏飞.全概率公式的推广[J].数学的实践与认识，2014，44（11）：313-316.IN FENG，WANG PENGFEI. Research of complete probabilitformula[J]. Mathematics in Practice and Theor，2014，44（11）：313-316.（in Chinese）

A Real-Time Evaluating Model of RAT ’s Hit Probabiliitt

DING Guang-qiang
（MilitarRepresentatives Bureau of NED in Shanghai, Shanghai 200129, China）

Abstrraacctt:: The real-time evaluating result of hit probabilitfor rocket assisted torpedo（RAT）is an important basis to com⁃mand and decision-making. Firstl, the RAT’s static hit probabilitsheet was obtained according to the distance and rela⁃tive bearing off the target. Secondl, the fire error distribution area was partitioned into some sub-zones, and the dropping probabilitinto each sub-zone the RAT’s water-entrpoint madrop was calculated. Thirdl, the average hit probabilitfor each sub-zone was accounted, which was based on its nodes’distance and relative bearing off the target, as well as the static hit probabilitsheet. Finall, the RAT’s real-time hit probabilitwas the sum of the multiplication of each subzone’s dropping probabilitand its average hit probabilit.

作者简介：丁光强（1964-），男，高工，硕士。

收稿日期：2014-11-02；

DOI:10.7682/j.issn.1673-1522.2015.02.011

文章编号：1673-1522（2015）02-0147-04

文献标志码：A

中图分类号：TJ565；O213.2

修回日期：2015-01-07