基于移动锚节点的WSN加权质心定位方法研究

严雨霞　冯友兵　孙小想

摘 要：针对传统加权质心定位算法锚节点数量多、定位精度低的问题，提出了一种利用单个移动锚节点实现加权质心定位的方法。该方法使锚节点沿着既定轨迹移动，并在移动过程中等间距广播信标信息，未知节点选择收到信标信息最近的4个虚拟锚节点构成未知节点所在的多边形，并利用接收信号强度确定权值，进而计算未知节点自身的位置。仿真结果表明，文中提出的算法比传统加权质心定位算法具有更好的定位精度，并可以通过调节信标间距改善定位精度。

关键词：无线传感器网络；节点定位；加权质心；移动锚节点

中图分类号：TP393 文献标识码：A 文章编号：2095-1302（2015）10-00-03

0 引 言

节点定位是无线传感器网络应用的关键技术之一，而质心算法是一种典型的无需测距的节点定位方法，仅仅依靠网络连通性实现定位，定位方法简单有效，但定位精度较低。加权质心算法充分利用接收信号强度（RSSI）信息，并采用了多种方法进行改进[1-4]，提高定位精度。但对于应用静态锚节点进行定位的WSN中往往都需要大量锚节点，而锚节点通常自带定位装置（如GPS），但成本较高。移动锚节点的使用可以有效减少锚节点数量，降低成本，已经在WSN定位方法中得到应用[5-8]。

本文在WSN中引入移动锚节点，且网络中只使用一个锚节点，利用锚节点的移动实现多个锚节点的作用，在降低网络投入成本的情况下实现节点定位，同时通过改变锚节点发送信标间距，使定位精度满足应用需求。

1 问题描述

1.1 网络模型

假设在某监测区域中部署了大量无线传感器节点构成WSN，为便于定位描述，构建二维直角坐标系，形成如图1所示的网络模型，并保证网络全部处于直角坐标系的第一象限。网络中所有传感器节点位置未知，有且只有一个可移动的带定位装置（如GPS）的锚节点，且锚节点移动方向和距离精确可控。网络部署起始阶段将移动锚节点安置在坐标原点处。本文的工作就是利用该移动锚节点实现对整个网络中所有未知节点的定位。

1.2 定位原理

定义：移动锚节点发出信标的位置称为虚拟信标位置，并认为该位置具有一个虚拟锚节点。

图1 网络模型

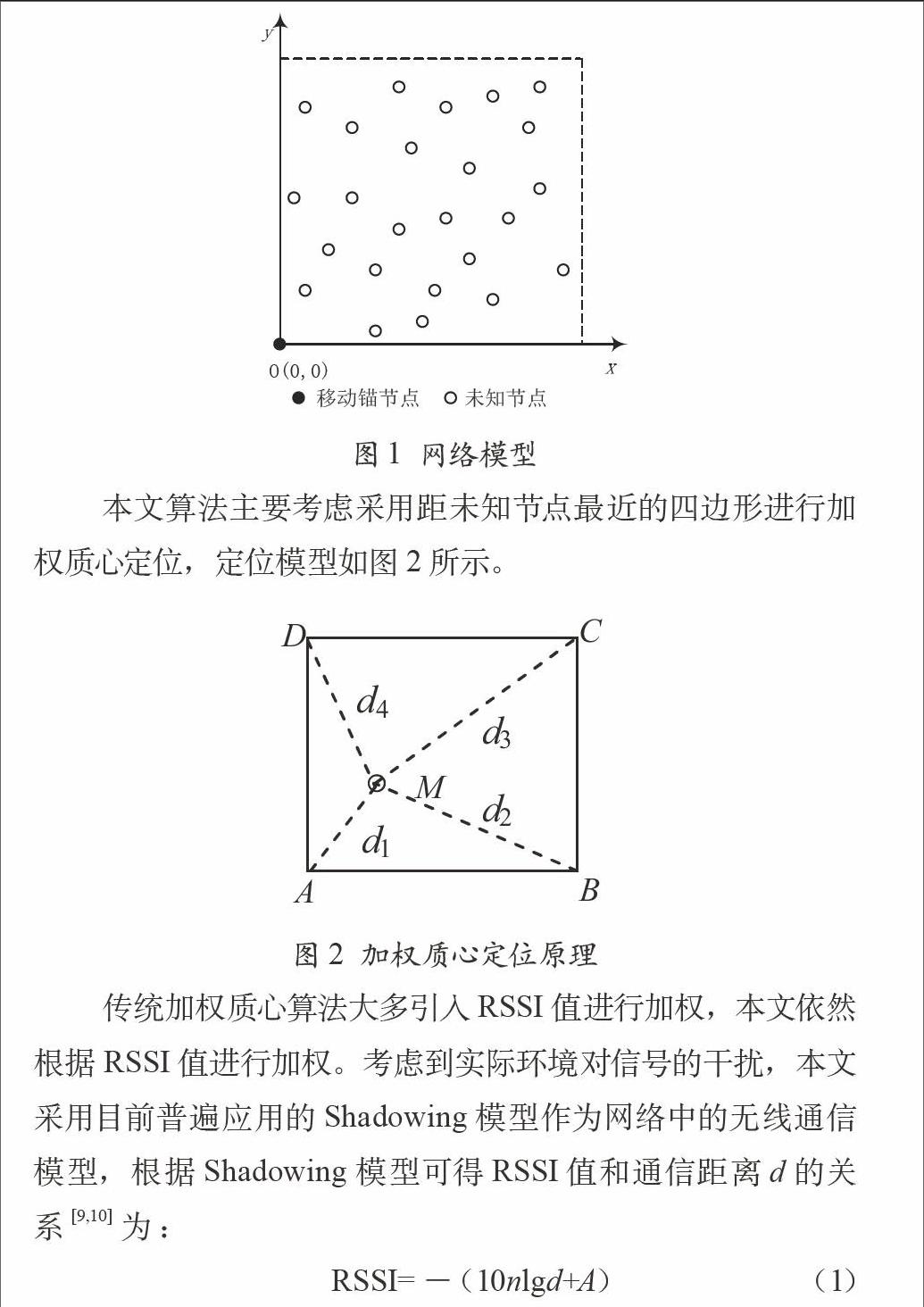
本文算法主要考虑采用距未知节点最近的四边形进行加权质心定位，定位模型如图2所示。

图2 加权质心定位原理

传统加权质心算法大多引入RSSI值进行加权，本文依然根据RSSI值进行加权。考虑到实际环境对信号的干扰，本文采用目前普遍应用的Shadowing模型作为网络中的无线通信模型，根据Shadowing模型可得RSSI值和通信距离d的关系[9，10]为：

RSSI=-（10nlgd+A） （1）

其中，RSSI为接收信号强度，n为与传输环境有关的信号传输常数，A为距离发射节点1米处的平均接收信号强度；d为发射节点与接收节点之间的距离。

在图2所示的四边形中，未知节点M处于A、B、C、D四个锚节点构成的四边形内部， 假设已经根据公式（1）获取未知节点M到锚节点A、B、C、D的估计距离分别为d1、d2、d3、d4，考虑到距未知节点越近的锚节点对未知节点位置的影响越大，则利用距离倒数计算权值，即有：

（2）

其中n=4，且。

则未知节点M的坐标为：

（3）

2 算法描述

为实现移动锚节点对整个网络的遍历，并形成多个虚拟锚节点，保证所有未知节点均处于某个多边形中，本文主要考虑容易实现的四边形结构。锚节点采用扫描方式实现移动，具体的移动方式如图3所示（以沿水平方向移动为例加以说明），锚节点沿着坐标轴（以x轴为例）和与坐标轴平行的分层线移动，实现扫描，直至遍历整个网络。其中分层线用于把网络在垂直方向上进行划分，网络分层时采用等间隔划分的方法，假设层高为h，h的大小可依据移动锚节点射程l、网络规模等来确定，且h

图 3 锚节点移动方式及定位示意图

网络分层完成后，未知节点的定位过程如下：

假设移动锚节点起始部署在坐标原点位置，当网络开始工作后，锚节点首先沿x轴方向移动，当锚节点到达网络右边界时，如图3中O1点，锚节点则转向沿O1O2方向向上移动，到达O2点后再沿O2O3方向向左移动直至到达O3点，实现第一层未知节点的遍历和定位。然后锚节点再沿O3O4向上移动，直至到达O4点后再沿O4O5向右移动，直到O5，依次类推直到锚节点通过整个网络。

在移动过程中，当锚节点处于x轴或分层线上时，以信标间隔广播一轮自身位置信息，未知节点接收并保存锚节点位置信息和接收信号强度。未知节点根据接收信号强度选择距离最近的四个虚拟锚节点，并将这四个虚拟锚节点构成的四边形作为未知节点所在的多边形，根据定位原理，即可计算出未知节点的位置坐标。

3 仿真与分析

为验证本文算法性能，应用Matlab仿真分析，并与传统加权质心算法比较，仿真参数如表1所列。

表1 仿真参数

参数 取值

网络规模 100×100

未知节点数 100个

移动间距 10

锚节点射程 30

仿真中，传统加权质心定位算法采用25个锚节点（占节点总数的20%），并均匀分布。而本文算法只采用1个移动锚节点。为更具可比性，两种算法均在同一种随机分布下进行定位比较。

3.1 定位结果

图4和图5分别为两种方法在同一种随机分布下的定位结果，对比可知，利用本文算法实现的节点位置与实际位置相差更小，图6是两种算法进行每个节点的定位误差比较，由图可知，绝大多数未知节点在利用本文算法进行定位时，定位误差明显小于传统加权质心定位算法，因此，本文算法具有更高的定位精度。

图4 传统加权质心算法定位结果

图5 本文算法定位结果

图6 定位误差比较

3.2 误差影响因素分析

通常情况下，很多因素都会对WSN定位误差产生一定的影响，本文主要选择信标间距、网络分层层高和节点分布密度进行分析：

（1）信标间距和网络分层层高

在确定的网络分布中，且网络分层固定的情况下，信标间距的改变直接表示虚拟锚节点的数量，信标间距越小，虚拟锚节点越多，即意味着虚拟锚节点占的比例越大，定位精度越高。图7即为在表1仿真参数下，改变信标间距，节点的平均定位误差，由图可知，随着信标间距的减小，平均定位误差减小，但当信标间距减小到5以后，定位误差基本不再发生变化，因此信标间距无需太小，满足实际应用的需求即可。

同理，网络分层层高实际上是另一个方向上的信标间距（在图3 所示网络中为垂直方向上的信标间距），因此，网络分层层高也无需过小。

图7 信标间距对定位误差的影响

（2）节点密度

在无需测距的定位方法中，尤其在依赖网络连通性的网络中，节点密度对定位误差具有很大的影响。本文算法改变网络节点数量，即在100×100的网络中，分别部署50，60，70，80，90，100，110，120个节点，其他参数依然采用表1所列的仿真参数，平均定位误差如图8所示，由图8可知，平均定位误差基本在1.6上下波动，且变化很小，因此，节点密度对本文算法没有影响。

图8 未知节点密度对定位误差的影响

4 结 语

本文提出的利用单个移动锚节点实现WSN加权质心定位的方法，具有以下优点：

（1）定位成本低。利用锚节点的移动实现多个锚节点的作用，减少了锚节点数量，降低了锚节点成本，且传感器节点不用配备额外的硬件。

（2）定位算法简单。本文算法是在传统加权质心定位方法的基础上改进，在定位过程中，传感器节点仅需接收锚节点信息即可实现定位，其原理依然是加权质心定位方法，算法复杂度低。

（3）定位精度高。信标间距对本文算法定位结果具有很大的影响，可通过减小信标间距增加虚拟锚节点密度提高定位精度，可根据网络应用的需要选择恰当的信标间距。

本文应用Shadowing模型分析RSSI和距离之间的关系，但实际应用场合往往很复杂，还需要具体问题具体分析。同时，本文算法也没有考虑实际应用中移动锚节点的移动速度对算法定位精度的影响，因此有必要作进一步研究。

参考文献

[1]杨新宇，孔庆茹，戴湘军.一种改进的加权质心定位算法[J].西安交通大学学报，2010，44（8）：1-4.

[2]李文辰，张雷.无线传感器网络加权质心定位算法研究[J].计算机仿真，2013，30（2）：191-194.

[3]刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权质心定位算法[J].传感技术学报，2010，23（5）：717-721.

[4] Lixiong Tan，Fei Luo， Kai Liu. Weighted centroid location algorithm in Wireless Sensor Network [C]. Wireless Mobile and Computing （CCWMC 2011），2011： 414-418.

[5]鲍金凤，游晓鹏.WSN 中移动信标辅助的加权质心定位算法[J].计算机技术与发展，2013，23（10）：27-30，35.

[6]钟森，周小佳，闫斌.基于移动锚节点的无线传感器网络三边质心定位[J].计算机测量与控制， 2009，17（7）：1438-1440.

[7] Jiang Jin-fang， Han Guang-Jie， Xu Hui-hui， et al.LMAT： Localization with a Mobile Anchor Node Based on Trilateration in Wireless Sensor Networks[C]. Global Telecommunications Conference， 5-9 DEC， 2011：1-6.

[8] Ou Chia-Ho. A Localization Scheme for Wireless Sensor Networks Using Mobile Anchors with Directional Antennas [J]. Sensors Journal， IEEE， 2011，11（7）： 1607- 1616.

[9] Awad A，Frunzke T，Dressler F.Adaptive distance estimation and localization in WSNs using RSSI measures[C].IEEE 10th Euromicro Conference on Digital System Design Architectures Methods and Tools，2007： 471 - 478.

[10]倪巍，王宗欣.基于接收信号强度测量的室内定位算法[J].复旦学报（自然科学版），2004，43（1） ： 72 -76.