岳阳洞庭湖大桥桥位设计风速推算

曾向红，杜东升，吴贤云

（湖南省气候中心，湖南 长沙 430100）

岳阳洞庭湖大桥桥位设计风速推算

曾向红，杜东升，吴贤云

（湖南省气候中心，湖南 长沙 430100）

利用岳阳气象站1953-2010年年最大风速观测资料，通过时距换算、高度换算及地形订正等处理，构建相当于开阔平地10m高度处10min平均年最大风速58年序列。根据极值Ⅰ型分布曲线，采用耿贝尔法计算出10m高处不同重现期（200年、100年、50年、20年、10年）基本风速，根据洞庭湖区测风塔与岳阳气象站相应时段10min平均月最大风速比值，外推得到岳阳洞庭湖大桥桥位设计风速。根据设计风速，取α=0.131，利用风速随高度变化的指数公式推算到300m以内各个高度层（70m内10m一层，70m以上间隔30m）最大风速。

洞庭湖大桥；风速；推算

引言

岳阳洞庭湖大桥是杭州至瑞丽国家高速湖南省临湘（湘鄂界）至岳阳公路的控制性工程，位于洞庭湖入长江交汇口处，洞庭湖大桥以北下游3km湘江入长江的咽喉地段，东起岳阳，西接君山，河道两岸均为湘江Ⅰ级阶地。东岸为岳阳市区，湘江河道边筑有防洪大堤，堤顶高程38.96m；西岸位于湘江河漫滩上，为君山芦苇农场芦苇地，地势平坦，地面高程26.5～29.5m。根据大桥设计方案，大桥为1480m+ 453.6m双塔双跨钢桁梁悬索桥。岳阳洞庭湖大桥是湖南省连接鄂、赣及长三角的重要通道，其建设对于杭瑞高速全线拉通具有重要意义。

由于现代大桥跨度越来越大，主塔和主梁越来越高，建筑材质越来越轻，风压与风灾成为了现代大桥设计中最重要的限制因子，从而对抗风设计提出了更高的要求。因此，本文利用岳阳气象站及洞庭湖测风铁塔观测资料开展杭瑞高速洞庭湖大桥设计风速推算的研究。

表1 岳阳地面气象观测场地、测风仪器变更情况一览表

1 资料

岳阳市气象站位于洞庭湖边，距离桥位约5km左右，岳阳气象站年最大风速资料及台站沿革资料来源于湖南省气象档案馆。由于观测场地、仪器种类及其离地高度、风速取值的时间间隔等对风的大小有着一定程度甚至很大的影响，因此有必要对岳阳气象站观测场地、仪器变更情况作详细的说明，见表1。

湖南省气象局在洞庭湖三江口区域建有三个70m测风铁塔，分别距桥位3至7km不等，具体详情见表2。

表2 洞庭湖三江平原测风铁塔情况

2 桥位区设计风速的推算

2.1 岳阳气象站年最大风速资料的换算和多年序

列的建立

依据中国气象局发布执行的 《地面气象观测规范》对最大风速作如下规定：某个时段内出现的最大10min平均风速值。为构成具有可比性的最大风速的样本序列，需对不同观测仪器和方法获取的实测记录数据进行换算。岳阳站实际采用资料为从1953 年1月1日-2010年12月31日，序列长度为58a。

湖南各气象站在上世纪七十年代及之前采用维尔德压板式风速表，是从定时观测两分钟读数的记录挑取最大风速，称为“定时两分钟最大风速”，必须进行“时距换算”，依据相关文献，关系式如下：

为了消除风仪离地面高度不同对风速大小的影响，需要利用对数公式或指数公式，将气象站风速观测仪器各离地面高风速统一换算到离地面l0m高处的年最大风速。在贴地层内，风速随高度变化的规律可用下列对数公式表示：

图1 岳阳气象站年最大分风速历年变化（M.s-1）

式中，Vn为高度为处的风速，Zn为已知高度Zh为处的已知风速，Z0为地面粗糙度高度，本文取值为0.05m。令为Zn10m，则Zh为地面气象站风速仪离地高度，可换算离地面l0m高处的年最大风速。

经过以上两种换算后，可得出岳阳气象站的年最大风速资料。

2.2 年最大风速序列的审查和订正

图2为岳阳气象站经时距换算和高度订正后的年最大风速变化趋势，由图1可知，岳阳站年最大风速均呈减小趋势。由表1可知，岳阳气象站随着城市化进程及迁站影响，周边地理环境有了显著变化。1976年后岳阳站地理环境由集镇变为市区，尤其在1981年迁到原站址西北向80m处后，观测场周边建筑物增多，观测到得风速明显减小。

通过采用滑动T检验法检查岳阳站年最大风速是否存在突变。滑动T检验方法（MTT法）如下：

其中为需要求解的判定值，分别以某时刻前、后两个时段要素的平均值，则分别为对应的时距，分别为对应的标准差。当时，可判定该序列前、后两时段的平均值存在显著差异或突变。

取，则：

取m为10a，m1+m2-2=18按自由度查表得T0.01= 2.878。由图2可知，岳阳气象站在1985年前后年最大风速发生负突变，年最大风速减少。

图2 岳阳气象站年最大风速10年滑动平均t检验

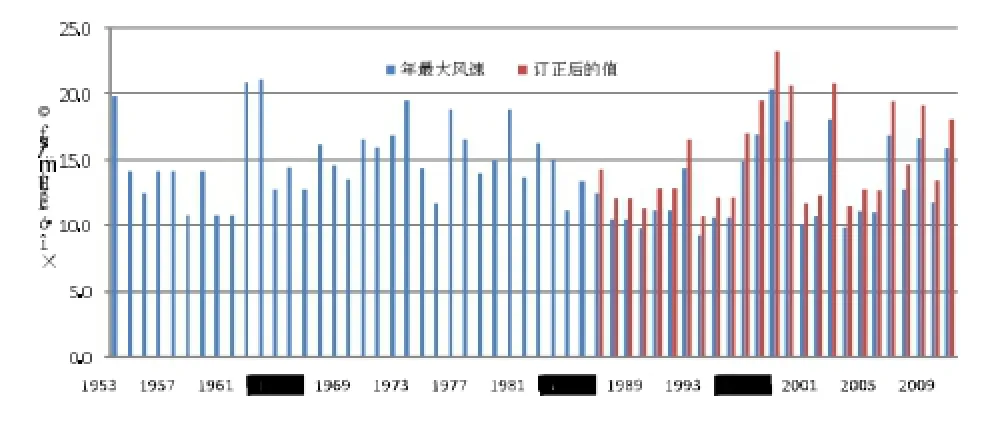
图3 岳阳气象站年最大风速变化（m.s-1）

通过计算可知，1953-1985年的岳阳站平均年最大风速为 15.3m.s-1，1986-2010年平均只有13.1m.s-1，两者相差2.2m.s-1，两者均值的比值为1.17，造成风速减小的显然与周边建筑物的增多与增高有关。利用比值法，将1986-2010年的年最大风速乘上1.17以消除风速不均匀现象。

2.3 气象站年最大风速的概率计算

《公路桥梁抗风设计指南》中对基本风速的确定方法有明确的要求：“桥梁所在地区的气象台具有足够的风速观测数据时，假设年最大风速服从极值Ⅰ型分布，由10min平均年最大风速100a重现期的数学期望值作为基本风速”。关于资料年限，国标《建筑结构荷载规范》（GB50009-2012）中有明确的要求：“选取的年最大风速数据，一般应有25年以上的资料”，通常大桥设计则要求30a以上的年最大风速数据资料。本文使用的资料为岳阳气象站经过订正的1953-2010年58a长序列资料，符合指南和规范对资料的要求。按指南的规定，利用极值Ⅰ型计算出不同重现期的基本风速，由于耿贝尔的参数估算法的估算误差较小，采用耿贝尔法计算出的基本风速。

极值Ⅰ型的分布函数是：

其超过保证率函数是：

令y=α（x-u），求得y的保证率函数为：

由此得到：

表3 岳阳气象站不同重现期的基本风速推算值（m.s-1）

以岳阳气象站年最大风速序列的均值E（XM）及σXM标准差作为及的近似估计值。而E（y）和σy的近似估计值及Sy只与N有关，有表可查。将上述四个估计值代入（12）、（13）式求出、，再将其代入（8）式可得：表3是利用极值Ⅰ型计算出岳阳气象站不同重现期的基本风速（m.s-1）。

同时利用矩法参数估算法对上述结果进行检验，两者结果完全一致。

2.4 桥位区设计风速的估算

为了求出桥位区设计风速，需将岳阳气象站的基本风速移植到桥位区。采用表2中距桥位较近的70m测风塔岳阳气象站风速进行相关分析。由于铁塔观测时间有限，测风塔10min平均月最大风速有效样本仅10个，但与同期岳阳气象站10min平均月最大风速相关系数为0.76，通过信度为0.01显著性水平。测风塔和岳阳气象站同期10min平均月最大风速的均值分别为11.33m.s-1和8.83m.s-1，其比值为1.28。因此可以将岳阳气象气象站不同重现期基本风速乘上风速增大系数1.28，但由于随着岳阳城市的迅速发展，岳阳市气象站在年最大风速和月最大风速呈减小的趋势，而统计的岳阳气象站不同重现期设计风速采用的是1953-1985年58a年最大风速资料，且岳阳气象站距桥位较近，靠近湖边，故风速增大系数不宜达到1.28，也不宜仅按公认的统计误差10%的一半进行修正，初步假设基本风速从气象站移植到桥位区的增大系数为1.2。从而可得到大桥桥位区的不同重现期10min平均年最大风速，重现期为100a的设计风速为32.9m.s-1，见表4。

表4 桥位区不同重现期的设计风速推算值（m.s-1）

2.5 风速随高度的变化

在500～1500m以下的大气摩擦层中，风速随高度的变化，最常用的模拟规律为指数律，即对摩擦层中任一高度z上的平均风速和标准高度zs上的风速有上式中，α为指数，地面粗糙度越大，α越大，且标准高度通常取为10m。

由于桥位区没有梯度风观测资料，但湖南省气象局为开展风能资源评估工作时在洞庭湖区先后建立了4座70m高测风铁塔，因此，这里采用其中2座距桥位较近的铁塔梯度风观测资料来推算风速随高度变化。

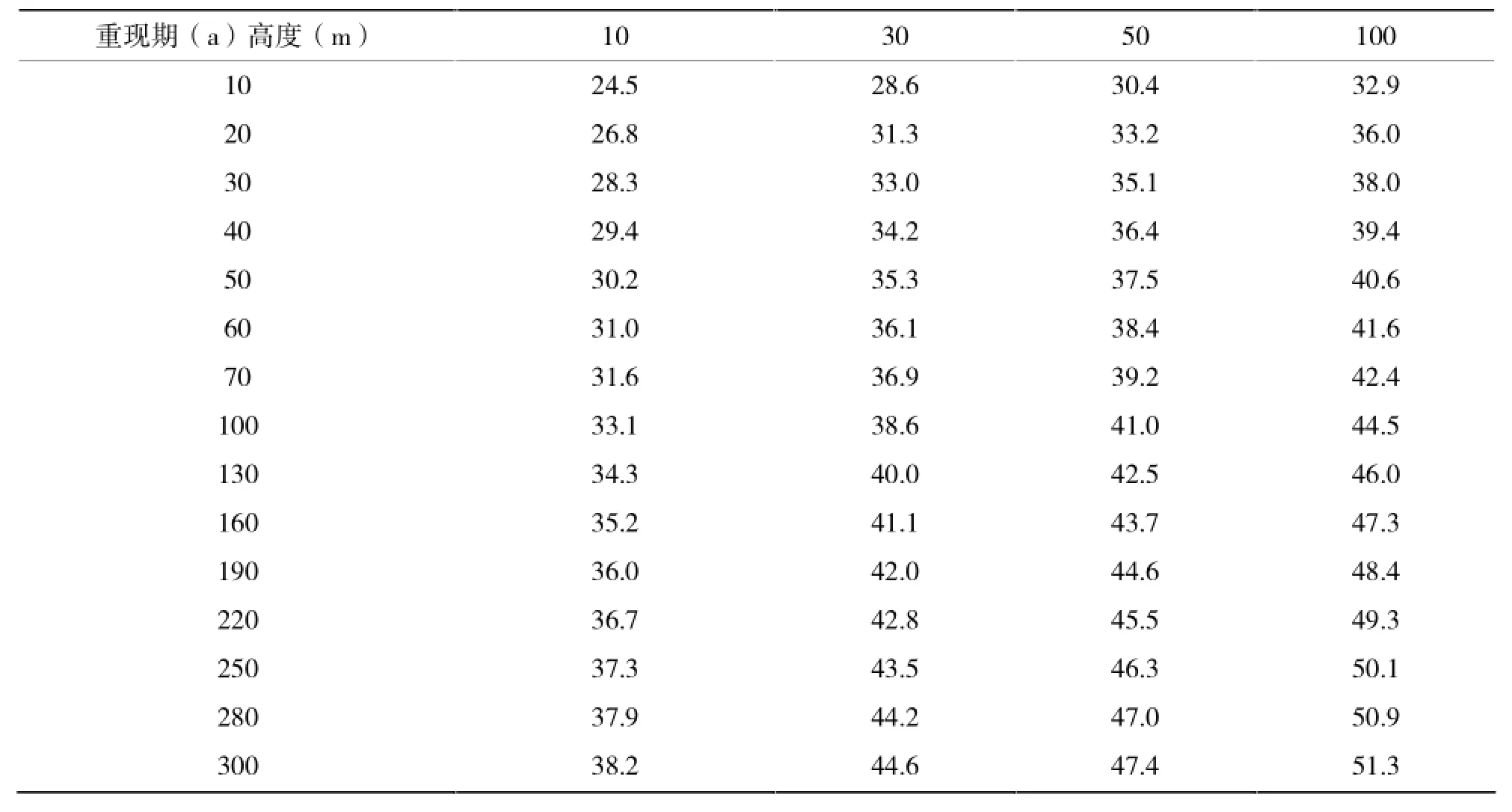
表5 各高度不同重现期的最大风速（m.s-1）

根据距桥位较近的70m测风塔1a实测资料，采用测风塔各层逐日的日最大风速为样本，运用风速随高度变化的幂指数公式以及最小二乘法计算，得到的2座测风塔的风切变指数基本接近，约为0.141；若选取日最大风速中≥5m.s-1的风速作为计算样本，得到的风切变指数约为0.131。

通过计算70m高度实际日最大风速序列与用10m高度风速按指数规律推求的70m高度拟合风速之间的相关关系来看，如果采用指数0.141，其相关系数为0.9440，绝对误差为0.787m.s-1，如果采用指数0.131，其相关系数为0.9442，绝对误差为0.786 m.s-1。这说明实际风速序列与拟合风速序列相关性很好，拟合的绝对误差小于1 m.s-1。表明采用指数规律来计算该区域风随高度的变化是合适的，且利用最大风速中≥5 m.s-1的样本来计算略优。因此，在后面的风速推算中，切变指数取0.131。

2.6 各高度层不同重现期最大风速的推算

根据大气边界层理论，摩擦层中风随高度变化符合指数律，指数值取决于湍流强弱变化，但就大桥设计所考虑的边界层状态，风速随高度变化的一级微商随高度是减小的，所以70m到300m高度间的指数值应略小于70m高度以下的值。但从安全性考虑，这里把该值用到70m高度以上，不再对此指数值作修正，而采用工程计算中指数值在摩擦层中均取同一值的方法，即对湖面指数值采用邻近岸边梯度塔的计算值。根据设计基本风速，取α=0.131，利用风速随高度变化的指数公式将10m高度上的最大风速推算到300m以内各个高度层 （70m内10m一层，70m以上间隔30m）（表5）。

3 结论

（1）采用岳阳气象站1953-2010年最大风速序列，利用极值Ⅰ型曲线，计算得到岳阳气象站不同重现期 （100、50、30、10年）10m高处10min平均年最大风速 （基本风速）分别为27.5m.s-1、25.3m.s-1、23.8m.s-1、20.4m.s-1。

（2）从气象站到桥位区的风速放大系数为1.2，计算得到桥位区不同重现期（100、50、30、10年）10m高处10min平均年最大风速 （设计风速）分别为32.9m.s-1、30.4m.s-1、28.6m.s-1、24.5m.s-1。

（3）基于桥位区附近测风铁塔≥5m.s-1的日最大风速随高度变化，推算得到风切变指数为0.131，由此计算得到200m以下每10m高度的设计基准风速。

［1］ 《公路桥梁抗风设计指南》编写组.公路桥梁抗风设计指南 ［M］.北京：人民交通出版社，1966.

［2］中国建筑科学研究院.中华人民共和国国家标准：建筑结构荷载规范 （GBJ50009-2002） ［M］.北京：中国建筑工业出版社，2002.

［3］中国气象局.地面气象观测规范 ［M］.北京：气象出版社，2003.

［4］陈正洪，向玉春，杨宏青.深圳湾公路大桥设计风速的推算 ［J］.应用气象学报，15（2）：226-233.

［5］张忠义，刘聪，居为民.南京长江第二大桥桥位风速观测及设计风速的计算 ［J］.气象科学，2000，20（2）：200-205.

［6］刘峰，许德德，陈正洪.北盘江大桥设计风速及脉动风频率的确定［J］.中国港湾建设，2002，（1）：23-27.

［7］秦鹏，黄浩辉，李春梅.珠江口海域热带气旋气候特征及最大风速计算 ［J］.气象研究与应用.2013，34 （2）：26-30.

［8］文元桥，陈正洪.荆岳长江大桥附近大风特征及设计风速推算研究 ［J］.武汉理工大学学报：交通科学与工程版，2010，34（2）：306-309.

［9］刘聪，黄世成，朱安祥，等.苏通长江公路大桥设计风速的计算与分析 ［J］.应用气象学报，2006，17 （1）：44-51.

［10］刘德辅，王莉萍，庞亮.多维复合极值分布理论在极端海况概率预测中的应用 ［J］.科学通报.2006，51 （9）：1112-1116.

［11］李增志，黄峰，朱福萌，等.超声风速温度仪的误差分析与检定方法研究 ［J］.气象研究与应用，2009，30（1）：58-59.

［12］王永林.对地面自动气象观测系统风速滑动平均计算方法的探究 ［J］.气象研究与应用，2009，30（2）：75-77.

［13］唐延婧，宋丹，柳艳香，等.贵州高速公路低能见度分类预报方法研究 ［J］.气象研究与应用，2015，36（1）：96-99.

［14］农成万，何如，邝良俊，等.广西沿海超高层建筑进行气象灾害风险评估必要性 ［J］.气象研究与应用，2014，35（1）：71-73.

［15］林中庆，曹亚平，赵小伟.风廓线雷达资料在一次强对流天气过程中的应用 ［J］.气象研究与应用，2011，32（3）：19-22.

Wind speed calculation for the location design of Dongting Lake Bridge in Yueyang

Zeng Xiang-hong，Du Dong-sheng，Wu Xian-yun

Based on annual maximum wind speed observation data of Yueyang weather stations during 1953-2010，average annual maximum 10 min wind speed，which is equivalent to the weed speed in 10 m height opening ground，sequence of 58 years was built by the distance conversion，height conversion and topographic correction processing.Based on extremumⅠ distribution curve line，the different return period of（200，100，50 years，20 years，10 years）basic wind speed in 10 m high was calculated by the Gumbel method.According to 10 min average monthly maximum wind speed ratio during the corresponding time between anemometer tower and weather station in Yueyang，wind speed design for the location of Dongting Lake Bridge was extrapolated.According to the wind-speed design，alpha （0.131）was taken by using the maximum wind speed in each levels wind within 300 m （$70 m in 10 m，70 m more than 30 m intervals）calculated by index formula of speed changing with height.

Dongting Lake Bridge；wind speed；calculation

P468.0+26

A

1673-8411（2015）04-0089-05

2015-05-13

交通运输部建设科技项目（编号：2013318798320）；湖南省交通科技项目（编号：201219）

曾向红（1962-），女，湖南长沙人，本科，高级工程师，主要从事应用气象工作，邮箱：zzxxhh@163.com。