Prediction of flow stress of 7017 alum inium alloy under high strain rate compression at elevated temperatures

Ravindranadh BOBBILI*，B.RAMAKRISHNA，V.MADHU，A.K.GOGIA

Defence Metallurgical Research Laboratory，Hyderabad 500058，India

Received 27 June 2014；revised 28 August2014；accepted 28 August2014 Available online 29October 2014

Prediction of flow stress of 7017 alum inium alloy under high strain rate compression at elevated temperatures

Ravindranadh BOBBILI*，B.RAMAKRISHNA，V.MADHU，A.K.GOGIA

Defence Metallurgical Research Laboratory，Hyderabad 500058，India

Received 27 June 2014；revised 28 August2014；accepted 28 August2014 Available online 29October 2014

An artificialneuralnetwork（ANN）constitutivemodeland Johnson-Cook（J-C）modelwere developed for 7017 alum inium alloy based on high strain rate data generated from split Hopkinson pressure bar（SHPB）experiments at various temperatures.A neural network configuration consistsof both training and validation，which iseffectively employed to predict flow stress.Temperature，strain rateand strain are considered as inputs，whereas flow stress is taken as output of the neural network.A comparative study on Johnson-Cook（J-C）model and neural network modelwas performed.Itwas observed that the developed neural network model could predict flow stress under various strain rates and temperatures.The experimental stress-strain data obtained from high strain rate compression tests using SHPB over a range of temperatures（25°-300°C），strains（0.05-0.3）and strain rates（1500-4500 s-1）wereemployed to formulate J-Cmodel to predict the flow stress behaviour of 7017 aluminium alloy under high strain rate loading.The J-Cmodel and the back-propagation ANNmodelwere developed to predict the flow stress of 7017 aluminium alloy under high strain rates，and their predictability was evaluated in terms of correlation coefficient（R）and average absolute relative error（AARE）.R and AARE for the J-Cmodelare found to be 0.8461 and 10.624%，respectively，w hile R and AARE for the ANN model are 0.9995 and 2.58%，respectively.The predictions of ANN model are observed to be in consistentw ith the experimental data for all strain rates and temperatures.

Aluminium alloy；Artificial neural network；Johnson-Cook model

1.In troduction

Themechanical properties aswellas deformation and fracturemechanisms at high strain rates are quite different from those exhibited under quasi-static loading.Hence the accurate predictionsmay notbedrawn from thequasi-static stress-strain data（10-3-10-1s-1）athighstrain rates（102-107s-1），and the useofsuchdatain theanalysisand designofdynam ically loaded structuresmay lead to erroneous conclusionsand designs.It is therefore essential to study the material deformation characteristicsathighstrain rates forapplicationsinvolvinghighstrain rate deformations.The data obtained ishelpful for the purpose of design of productsaswellas for developing the constitutive strengthmodelsof thematerials.In order to developm ore robust strength models and failure criteria under dynam ic loading，more andmore experimental data obtained overw ide range of strain rates is required.An iterative procedure involving dynamicmaterial testing and computermodellingmay reduce the time and expense required for the development of advanced materials for applications such asarmour.Characterization of deformation，fracture and load carrying capability ofmaterials subjected to high strain rate isparamount foroptimum material selection fordesign ofarmourmaterialswhich experiencehigh strain rate dynam ic deform ation during impact of projectiles，blast loading，explosive form ing and other impactevents.

Various high strain rate testmethods，such as drop weight，split Hopkinson pressure bar（SHPB），gasgun，Taylor impact and expanding ring，were reported in Refs.［1-5］.SplitHopkinson pressure bar testmethod has been extensively used fortesting in thestrain rate regimeof102-104s-1in tensionand compression modes［2，3］.The three important considerations intrinsic to high strain rate testing arewavepropagation，influenceofstrain rateondeformationofmaterials，andeffectofhigh strain rate and temperature on propertiesofmaterials［2］.

The effect of strain rate on material properties，viz.，flow stress，strain rate sensitivity，etc.，varies for eachmaterial.An increase in ductility of Al 7075 alloy was also reported by M agd et al.［2］.Metallographic investigations of thematerial showed ductile shear failure.Existence of two regionsof strain rate sensitivity in A l 7075 over a range of strain rates was exp lained by Lee et al.［6］.Itwas reported that the strain rate hasonly slighteffecton flow stress in the strain rate regime of 102-103s-1，which is higher than 103s-1at strain rates，and the flow stress increasesmore rapidly w ith strain rate having an approximate linear relationship.Hou et al.［7］carried out the high strain rate experiments on Mg-Gd-Y alloy using SHPB over a range of temperatures.A modified J-Cmodel was proposed to predict the dynamic response of thismaterial over aw ide range of strain rates and temperatures.

Ji et al.［8］carried out the hot com pression tests on Aerm et100 steel using Gleeble-3800 thermo-mechanical simulator to generate stress-strain data in a temperature range from 1073 to 1473 K and a strain rate range from 0.01 to 50 s-1. The Arrhenius constitutivemodel and feed forward artificial neural network（ANN）model were developed to predict the high temperaturedeformation behaviourof theabovematerial. ANN was found to be superior formodelling the high temperature deformation behaviours ofmaterials.Han et al.［9］performed a comparative study on constitutive relationship of 904L Austenitic steel during hot deformation based on A rrheniusand ANN models.Experim ental datawere gathered from hot compression tests on Gleeble-1500D thermo-mechanical simulator to generate stress-strain data，in a temperature range from 1000 to 1150°C and a strain rate from 0.01 to 10 s-1.The back-propagation neural network model was proved to bemore accurate and efficient in investigating the compressive deformation behaviour of material at higher temperatures.Sun etal.［10］employed ANNmodel to develop a constitutivemodel for the hot compression of Ti600 alloy. These tests were performed on Gleeble-1500 thermo-mechanical simulator in a temperature range from 800 to 1100°C and a strain rate range from 0.001 to 10 s-1to generate stressstrain data.ANNmodel provided a simple and efficientway to develop constitutive relationship for Ti600 alloy.Lin etal.［11］studied the compressive behaviour of 2124-T851 alum inium alloy under the strain rate from 0.01 to 10 s-1and the temperature from 653 to 743 K using Gleeble-1500 thermo-mechanical simulation machine.A modified constitutivemodel accommodating the effects of material behaviour was proposed.Gupta［12］developed various sem i-empiricalmodels（Johnson-Cook model，modified Zerilli-Armstrong model and A rrheniusmodel）to study the effects of strain，strain rate and temperature.The tensiles of Austenitic stainless steel 316 were test using UTM machine at various strain rates（0.1-0.0001 s-1）and temperatures（323-623 K）.A comparative study was undertaken among various constitutive models and ANN model.

The available literature has so far dealtw ith dynamicmaterial characterization of variousmaterials and their testing methodologies under different loading conditions，and microstructural analysis of various steels.So far no attempt has been made to study the effect of temperatures of 7017 alum inium alloy on dynamic properties using J-C and ANN models.The objective of the present study is to develop ANN model for predicting the dynam ic flow stress of 7017 alum inium alloy under high strain rate loading conditions.

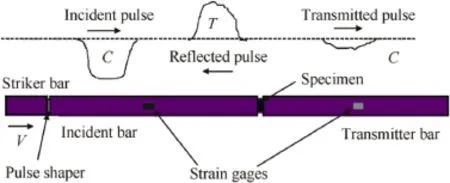
Fig.1.Schematic diagram of Split Hopkinson pressure bar（SHPB）.

2.Experim en talm ethods

2.1.Materials and test setup

The present alloy under study is Al-4.5 Zn-2.5 Mg-0.3Si-0.40 Fe（by weight%），commercially named as 7017 alum inium alloy.The quasi-static yield and ultimate tensile strengthsof the alloy are 458MPa and 508MPa，respectively. Ductilitymeasured as percentage elongation is13%in 25mm gage length.High strain rate compression testing of 7017 alum inium alloy sam ples w ith 3，4，5 mm in length and 6，8，10 mm in diameter was carried out using SHPB apparatus（Fig.1）.The specimenswere prepared w ith L/D ratio of 0.5，so as tom inimize the errors due to inertia and friction.Fig.2 shows the dimensions and surface finish of compressed specimen used for 20mm pressure bars.Length and diameter of the sampleswere changed to vary the strain rate.

The experimental stress-strain data were obtained from high strain rate compression tests using split Hopkinson pressure bar（SHPB），over aw ide range of strains（0.05-0.3），strain rates（1500-4500 s-1）and temperatures（25°-300°C）. The whole SHPB setup consists of pressure bars，gas gun which propels a striker bar for producing the compressive wave，strain gage for measuring the waves，associated mounting and alignment hardware，and associated instrumentation and data acquisition system.SHPB apparatus has two-pressure bars，one is called input or incident bar and another is called outputor transmitted bar［7］.These pressure bars aremade ofmaterials having yield strength higher than that of thematerial to be tested.The specimen to be tested is sandw iched between the 2 bars.The yield strength of the pressure bar determ ines themaxim um stress attainable w ithin the deform ed specimen，because the cross section of the specimen approaches to that of the pressure bar duringdeformation（Fig.3）.A rectangular compression wave w ith well-defined amplitude and length isgenerated in the incident barwhen the striker bar strikes it.

The pressure wave was generated by having a striker bar（projectile）to impact the input（incident）pressure bar.The striker bar was propelled by a gas gun system attached at one end.The strain gages in conjunction w ith the amplifiers and associated instrumentation were used to record these wave pulses.Since the specimen deforms uniform ly，the strain rate w ithin the specimen is directly proportional to the amplitude of the reflected wave（εr）.

Strain rate in the specimen is

Hence strain in the specimen is

Stress in the specimen can be calculated as

where A and Asare the areas of the bar and specimen，respectively；l is the length of specimen；c iswave speed；εtis the strain in the transm itted bar；and E is the elasticmodulus of the pressure bar.

2.2.Johnson-Cookmodel

High strain rate plastic deform ation of materials can be described by various constitutive equations that basically attempt to address the dependence of stress on strain，strain rate and temperature.In this regard，thestress can bepresented as

Thereare anumberof equations thathavebeen proposed to describe the plastic behaviour of materials as a function of strain rate and temperature.At low strain rates，themetals are known to work hardening along thewell-known relationship，which is known as parabolic hardening and expressed as σ=σo+kεn，whereσois the yield stress，n is the work hardening exponent，and k is the pre-exponential factor.

The effect of strain rate on strength is generally expressed as：σ∝ln.ε.But the above relationship breaks down at strain rate above 102s-1.

The effects of temperature on the flow stress can be represented by

where Tmis the m elting temperature；Tris the reference tem perature atwhichσris the reference stress.

The dynam ic flow stress depicting the effects of various parameters is expressed by Johnson-Cook model as

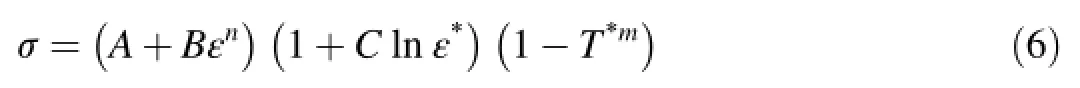
where A is the yield stress；B and n represent the effect of strain hardening；C is the strain rate constant；εis the equivalent plastic strain；.εis the strain rate；.ε*is the dimensionless p lastic strain rate represented as.ε/.εofor.εo=1 s-1；T*is the homologous temperature referred as（T-Troom）/（Tmelt-Troom）；and m is the thermal softening factor.Thus，the terms presented in first，second and third brackets in Eq.（6）represent strain，strain rate and temperature effect，respectively.The J-Cmodel is independent of pressure.

e strain rate and reference temperature，the functions of strain rate hardening and thermal softening are equal to unity，J-Cmodel is simplified as follows

where A is the yield stresswhich can be directly obtained from the strain-stress curve.

Plotting a line between lnεand ln（σ-A）at the reference strain rate and reference tem perature gives B and n in Eq.（7）. Strain rate sensitivity C is determ ined as the slope of linear fit of log（strain rate）vs the dynam ic flow stress/static stress using high strain rate data corresponding to a strain of 10%. The above constantsare provided in the Table 1.

Fig.2.Typical dimensions of high strain rate test samples.

Fig.3.Schematic of the deformed specimen tested at a strain rate of 4500/s.

2.3.Artificial neural network approach

Neural networks are commonly employed in data prediction，categorization and data filtering app lications.A rtificial neural networks（ANN）im itate human brains to know the interaction between inputs and outputs through training.Multi-layer ANN possesses input layers，hidden layers and output layers.The hidden layers located between input and output layers.The input layer first receives data and conveys it to the hidden layer for processing.The processed data is delivered as response to the output layer.Each layer can geta number of neurons connected by linksw ith adaptableweights. These weights are adjusted during training.The inputs into a neuron aremultiplied by their respective connection weights，and summed together，and abias isadded to thesum.Thissum is converted through a transfer function to produce a single output.The nonlinear logarithm ic sigmoid activation function wasadopted in thehidden and output layers.Theactualoutput obtained is compared to the required output to compute an error.The error for hidden layers is calculated by propagating back the error found out for the output layer；this technique is called back-propagation algorithm.

The experimental data were sp lit into three sets，70%for the training set，15%for the verification set and 15%for the test set in ANN model.The input data（strain rate，strain and temperature）and outputdata（flow stress）were standardized in the range.Thenetworkmodel consistsof ten hidden layers.To demonstrate the influence of network variables，the number of hidden layer neurons were varied from 10 to 40.It has been noticed that the predicted results are reasonable and accurate，w ith 15 neurons in each hidden layer.

Table 1 Johnson-Cook M odel constants for A l 7017 alloy.

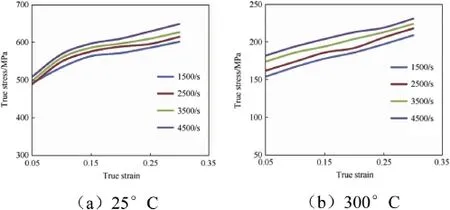
Fig.4.True stress-strain curves of aluminium 7017 alloy at temperatures 25°C and 300°C.

3.Resu lts and discussion

The experimental data obtained from the high strain rate compression tests（Fig.4）on splitHopkinson pressure bar in a w ide range of temperatures（25°-300°C）and strain rates（1500-4500 s-1）were employed to develop J-Cmodel and ANN model for 7017 alum inium alloy.Fig.5 depicts the comparison of the experimental results w ith the predicted values at various strain rates and temperatures based on J-C strength model.It is observed that the predicted flow stress values obtained on J-C model are not consistent w ith the experimental values，particularly at high temperatures；the predicted valuesare smaller than the experimental results.So，J-C model is not so adequate in predicting the flow stress value in high temperature region.The predicting performance of the J-C model was evaluated by comparing the experimental and predicted data，as shown in Fig.5.Itwas noticed that the J-Cmodel could predict the experimental data only in the interm ediate temperature range.This variation may be attributed to the error introduced by the fitting of them aterial constants at som e conditions and the adiabatic temperature increment due to plastic deformation.Since J-C model is a phenomenologicalmodel，which does not consider the physical aspects of materials like theory of thermodynam ics，thermally activated dislocation movement，and kinetics of slipswhile predicting the flow stress.

The J-C model and the back-propagation ANN model were developed to predict the flow stress of 7017 aluminium alloy under high strain rates and their predictability was evaluated in terms of correlation coefficient R and average absolute relative error（AARE）.The predicted flow stresses of J-Cmodelare given in Fig.5.Fig 6 illustrates the flow stress predicted by ANN model versusmeasured value for testing set.R and AARE for the J-Cmodelare found to be0.8461 and 10.624%，respectively（Fig.7），while R and AARE for the ANNmodel are 0.9995 and 2.58%，respectively（Fig.8）.It is found that the relative error obtained from the ANN model was observed to vary from 1.2%to 4.5%，while itwas in the range of 4.2%-10.6%for J-C model.The performance of the network also relies on learning parameters，such as the number of training epochs and the momentum，etc.To understand the significance of these parameters，the number of epochs is varied from 1000 to 10，000，the learning rate is varied from 0.1 to 0.9，and themomentum rate is varied from 0.1 to 0.8.Itshows that themomentum rate doesnotexhibita substantial influence on the performance of the network.It is established that the optimum number of epochs is about 12，000，the number of neurons in each hidden layer is15，thenumber of hidden layers is 10，and the learning rate is 0.8，w ith a momentum of 0.7 in all layers.Mean square errors（MSEs）of desired and predicted data have been determ ined when MSE attained am inimum value of 0.001.

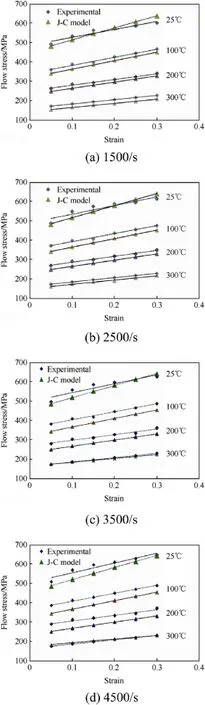
Fig.5.Comparison between J-C M odel and experimental flow stress of alum inium 7017 alloy by J-C model at strain rates.

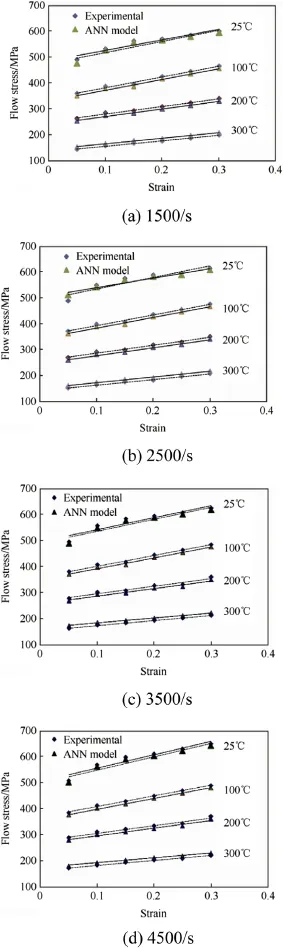
Fig.6.Comparison between ANN Model and experimental flow stress of alum inium 7017 alloy at strain rates.

Hence，the data obtained in the ANN m odel were better compared to the J-Cm odel.Itshow s that the developed ANN model can offer an efficient prediction of flow stress in the temperatures from 25°C to 300°C and strain rates from 1500 to 4500 s-1.

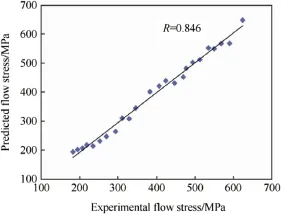
Fig.7.Plotof predicted vs.experimental formodified J-Cmodel.

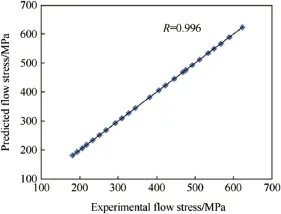
Fig.8.Plotof predicted vs.experimental for ANN model.

4.Conclusions

This paper hasmade an attempt to study the comparison of the results obtained from J-C model and ANN model with experimental values.The follow ing conclusions are drawn：

1）The J-C model and the back-propagation ANN model were developed to predict the flow stress of 7017 aluminium alloy underhigh strain rates，and their predictability wasevaluated in termsof correlation coefficient R and averageabsolute relative error（AARE）.R and AARE for the J-C model are found to be 0.8461 and 10.624%，respectively，while R and AARE for the ANNmodelare 0.9995 and 2.58%，respectively.

2）The established ANN model can effectively predict the experimental data over a w ider range of temperatures and strain rates.This represents that ANN model has superior capability tomodel the dynam ic behaviour ofmaterials.This method circumvents the problems related to the constitutive models that involve the determination of more number of constants.

3）The validation tests have also been conducted to verify the resultsobtained by ANN technique.The predictionsof the ANN m odel were in good agreement w ith the experimental data obtained from SHPB tests.

Acknow ledgem en ts

The authors would like to thank Defence Research and DevelopmentOrganization，India for financialhelp in carrying out the experiments.

References

［1］LeeWS，Lin CF.Plastic deformation and fracture behaviour of Ti-6Al-4V alloy loaded w ith high strain rate under various temperatures.Mat Sci Eng A 1998；241（1-2）：48-59.

［2］El-M agd E，Abouridouane A.Characterization，modeling and simulation of deformation and fracture behaviourof the lightweightw roughtalloys under high strain rate loading.Int JImpact Eng 2006；32：741-58.

［3］MousaviASH，M adaah-HosseiniHR，Bahram i.Flow stress optim ization for 304 stainless steel under cold and warm compression by artificial neuralnetwork and genetic algorithm.JMater Design 2007；28：609-15.

［4］Odeshi AG，Al-Ameeri S，Bassim MN.Effect of high strain rate on plastic deformation of a low alloy steel subjected to ballistic impact.J Mat Process Tech 2005；162-163：162-3.

［5］Mohr D，Gary G，Lundberg B.Evaluation of stress-strain curve estimates in dynamic experiments.Int J Impact Eng 2010；37：161-9.

［6］Lee WS，Sue WC，Lin CF，Wu CJ.The strain rate and temperature dependence of the dynam ic impactproperties of 7075 alum inium alloy.J Mat Process Tech 2000；100：116-22.

［7］Hou QY，Wang JT.A modified Johnson-Cook constitutivemodel for Mg-Gd-Y alloy extended to aw ide range of temperatures.ComputMater Sci 2010；50：147-52.

［8］Ji G，Li F，Li Q，Li H，Li Z.A comparative study on Arrhenius-type constitutivemodel and artificial neural network model to predict hightemperature deformation behavior in Aermet100 steel.J Mater Sci Engg A 2011；528：4774-82.

［9］Han Y，Qiao G，Sun J，Zou D.A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comput Mater Sci 2013；67：93-103.

［10］Sun Y，Zeng WD，Zhao YQ，Qi YL，Ma X，Han YF.Development of constitutive relationship model of Ti600 alloy using artificial neural network.ComputMater Sci2010；48：686-91.

［11］Lin YC，Xia YC，Chen XM，Chen MS.Constitutive descriptions for hot pressed 2124-T851 alum inium alloy over a wide range of temperature and strain rate.ComputMater Sci2010；50：227-33.

［12］Gupta AK，Anirudh VK，Singh SK.Developmentof constitutivemodels for dynam ic strain aging regime in Austenitic stainless steel 304.M ater Des 2013；43：410-8.

.Tel.：+40 24346332；fax：+40 24342252.

E-mail address：ravindranadhbobbili@gmail.com（R.BOBBILI）.

Peer review under responsibility of China Ordnance Society.

http：//dx.doi.org/10.1016/j.dt.2014.08.004

2214-9147/Copyright©2014，China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.

Copyright©2014，China Ordnance Society.Production and hosting by Elsevier B.V.All rights reserved.