制动力作用下漂浮体系中承式拱桥的梁轨相互作用研究
2015-11-05高卫卫
高卫卫
摘 要:以某漂浮体系中承式拱桥为工程背景,采用桥上无缝线路分析理论,建立制动力作用下的梁轨相互作用模型,研究了拱肋横梁与桥面的纵向相对位移、梁轨快速相对位移及钢轨制动附加力。结果表明:当偏安全考虑、不计硬木的弹性约束作用时,拱肋横梁与桥面的纵向相对位移最大值为1.8 mm,梁轨快速相对位移不超过0.8 mm,该纵向限位方案能够满足安全运营要求。
关键词:漂浮体系 拱桥 制动力 梁轨相互作用
中图分类号:U448 文献标识码:A 文章编号:1674-098X(2015)09(a)-0060-02
Abstract:The engineering background of this paper is a half-through arch bridge of floating type. Base on the theory of CWR on bridge, a model of interaction between beam and rail under braking force was built to analyze relative displacement between arch ribs cross-beam and deck, rapid relative displacement between beam and rail, as well as additional force in rail. For safety reason, the elastic constraint effect of hardwood was not considered. The calculation results show that the relative displacement between arch ribs cross-beam and deck is 1.8 mm, the rapid relative displacement between beam and rail is 0.8 mm, and thus the longitudinal stop design meets safety operation requirements.
Key Words:Floating Type;Arch Bridge;Braking Force;Interaction Force Between Beam and Rail
桥上铺设无缝线路后,在列车制动情况下,列车在轨面施加纵向水平力,这被称为制动力。制动力在长钢轨中产生变形和附加力,由于受到桥梁约束,将使桥梁产生变形。在常规桥梁设计中,制动力一般是通过固定支座,经墩台传递到桥梁基础[1-3]。但在实践中,经综合考虑经济性、行车条件等因素后,部分桥梁被设计成不设置纵向固定支座,此时制动力作用下的梁轨相互作用问题比较复杂。
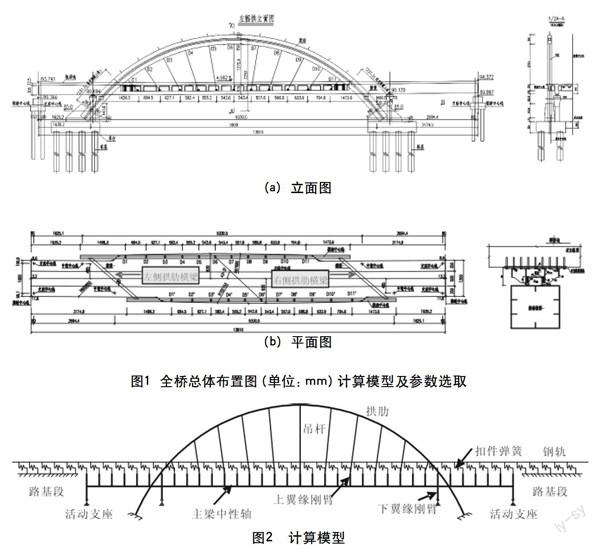
图1为某客运专线中承式拱桥,与公路斜交角为43.5°。主梁全长138.1 m,主纵梁、小纵梁、横梁组成纵横梁体系,并与桥面板连接、整体受力。左、右幅拱肋跨度均为90 m,且非对称布置,吊索倾斜布置。左、右幅拱肋分别由4个群桩基础支承,相邻承台之间由横向的承台系梁连接。全桥共设置4个中墩、4个边墩,4个中墩坐落在拱脚承台上。
全桥共设置4个纵向活动支座、4个双向活动支座,即采用纵向漂浮体系。为实现主梁纵向限位,设置如图1(b)所示的左、右侧拱肋横梁,横梁两侧各有一块硬木,厚度50 mm,高175 mm,长590 mm,与主纵梁外伸牛腿顶紧。针对这种构造处理,本文采用桥上无缝线路分析理论,考察制动力作用下的梁轨相互作用,旨在为同类工程提供参考。
1 计算模型及参数选取
1.1 计算模型
采用桥上无缝线路分析理论,建立如图2所示的计算模型,该模型采用连接弹簧来模拟扣件纵向阻力;采用刚臂连接主梁上翼缘、主梁中性轴和支座,通过释放约束模拟活动支座。扣件纵向阻力按照文献[4]取值:有载时,r=20u(u≤0.5 mm),r=10(u>0.5 mm);无载时,r=13u(u≤0.5 mm),r=6.5(u>0.5 mm)。桥梁两端路基固定区长度取为100 m,采用与桥上相同的扣件纵向阻力。采用有限元软件ANSYS建立仿真模型,其中:钢轨、主梁、拱肋采用Beam188梁单元,单元长度为0.5 m;吊杆采用link10索单元;弹簧单元采用Combin14弹簧单元,扣件弹簧采用非线性弹簧刚度系数。
1.2 计算工程
最后计算得到的每个车轮下的制动力Pz=21.165 kN,按集中力的形式加载到钢轨上。考虑单线制动,加载范围内的扣件纵向阻力采用有载阻力模型,其余地段采用无载阻力模型。
2 计算结果
2.1 CRH2动车组制动
考虑CRH2动车组在桥上不同位置制动,车速为200 km/h。列车从左侧上桥,运行至第8节车第4个轴离开右侧桥梁为止。偏安全考虑,不计虑硬木的弹性约束作用,即计算模型中拱肋横梁与桥面无连接关系。
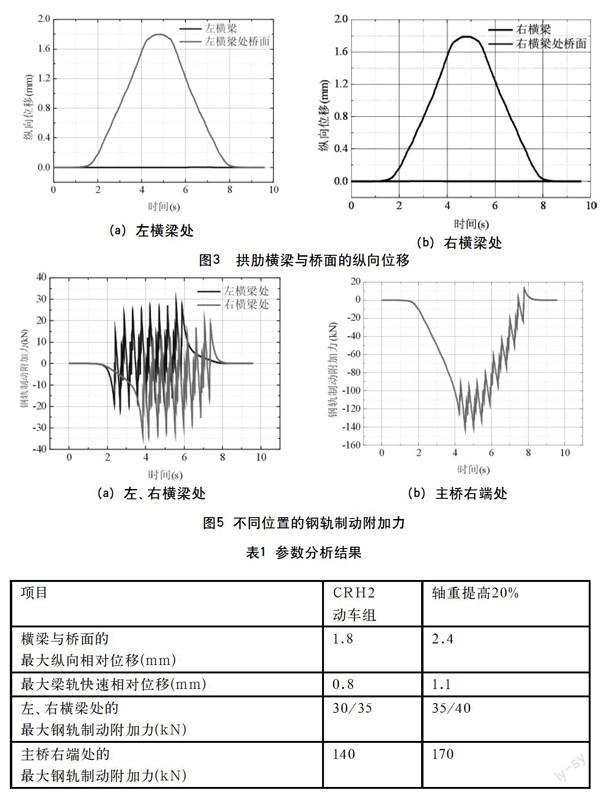
图3给出了左、右侧拱肋横梁处,横梁与桥面的纵向位移。可以看出:左、右侧横梁与桥面的最大纵向相对位移为1.8 mm;左、右横梁处的最大纵向相对位移发生在同一时刻;拱肋横梁的纵向位移几乎为0,即梁轨纵向力均通过吊杆传递到拱肋中。
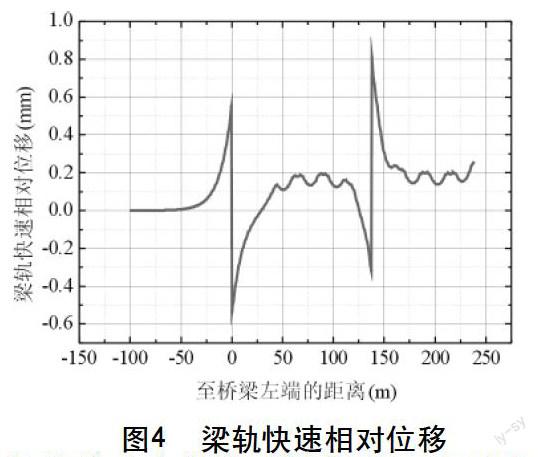
图4给出了动车组在主桥右端制动时的梁轨快速相对位移。文献[4]规定:在制动附加力计算工况下,无伸缩调节器时,梁轨快速相对位移最大不得超过4 mm。计算得到最大梁轨快速相对位移为0.8 mm,满足规范要求。
图5给出了左、右拱肋横梁处及主桥右端的钢轨制动附加力。可以看出:左、右横梁处的最大钢轨制动附加力分别为30 kN、35 kN;主桥右端处的最大钢轨制动附加力为140 kN。
2.2 参数分析
我国使用的高速列车车型较多,但其它高速列车的编组形式、车辆轴距、定距等参数与CRH2动车组基本相近,故这里仅考虑轴重(轨面制动力率)的变化,以此进行参数分析。
根据1.2节的计算,将轴重提高20%,再次进行分析,表1给出了计算结果。可以看出:横梁与桥面的最大纵向相对位移为2.4 mm,增大33.3%;最大梁轨快速相对位移为1.1 mm,增大37.5 %,但仍满足规范要求;左、右横梁处的最大钢轨制动附加力分别为35 kN、40 kN,分别增大16.7%、14.3%;主桥右端处的最大钢轨制动附加力为170 kN,增大21.4%。
3 结论
列车在桥上制动时,拱肋横梁与桥面的纵向相对位移非常小,最大值在1.8 mm左右(偏安全考虑,不计横木的弹性约束作用)。梁轨快速相对位移不超过0.8 mm,满足规范要求,该纵向限位方案能够满足运营安全要求。
参考文献
[1] 广钟岩,高慧安.铁路无缝线路[M].北京:中国铁道出版社,2012.
[2] 中华人民共和国铁道部.TB 10002.1-2005铁路桥涵设计基本规范[S].北京: 中国铁道出版社,2005.
[3] 中华人民共和国铁道部.TB 10002.3-2005铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].北京:中国铁道出版社,2005.
[4] 中华人民共和国铁道部.TB 10015-2012铁路无缝线路设计规范[S].北京: 中国铁道出版社,2012.
