力伺服波浪补偿器控制研究及其性能优化

周明健，王幼民



力伺服波浪补偿器控制研究及其性能优化

*周明健1，王幼民2

(1. 巢湖学院电子工程与电气自动化学院，安徽，巢湖 238000；2. 安徽工程大学机械与汽车工程学院，安徽，芜湖 241000)

力伺服波浪补偿器广泛应用于海洋工程领域，研究力伺服波浪补偿器的控制系统具有重要意义。建立了其数学模型，运用前馈复合控制方法消除作用在液压马达输出轴的外负载力矩的扰动干扰。基于消去扰动干扰的系统的数学模型，分析了系统的稳定性、能观性、能控性，运用极点配置方法对系统的控制性能进行优化，得到反馈矩阵。通过仿真验证了优化后系统的控制性能达到了优化设计目标。

力伺服波浪补偿器；前馈复合控制；极点配置方法；控制性能优化

0 前言

为了减少海上作业受到复杂海况的影响，补偿器成为海洋工程装备中重要组成部分之一，其控制性能优劣直接影响海上作业的效果[1-2]。补偿器可以分为位置补偿器、速度补偿器、力补偿器。

力伺服波浪补偿器是将力伺服液压控制技术与波浪补偿起重技术相结合，由液压执行元件、伺服阀、传感器、伺服放大器、A / D、D / A转换模块、计算机、液压伺服系统等组成[3]，用来减小海上作业时起吊绳索受海浪影响产生的交变载荷，从而避免起吊绳索出现断裂而危害人身和财产安全的现象发生[4]。

1 力伺服波浪补偿器的数学模型

1.1 力伺服波浪补偿器的控制过程方框图

力伺服波浪补偿器的控制过程[5]如图1所示，由伺服放大器环节K、阀控马达环节G、干扰传递函数环节G、液压绞车环节K、力传感器环节K组成，作用在马达上的外负力矩T是影响马达输出扭矩的干扰因素。以船舶竖直升降为输入信号和经过力传感器K反馈的钢缆拉力信号U进行比较，得到偏差信号，再将此信号通过伺服放大器控制伺服阀的位移进而控制液压马达的输出扭矩T来减小绳索所受的交变载荷，在控制绳索所受的交变载荷大小的同时，控制了起吊重物的速度。

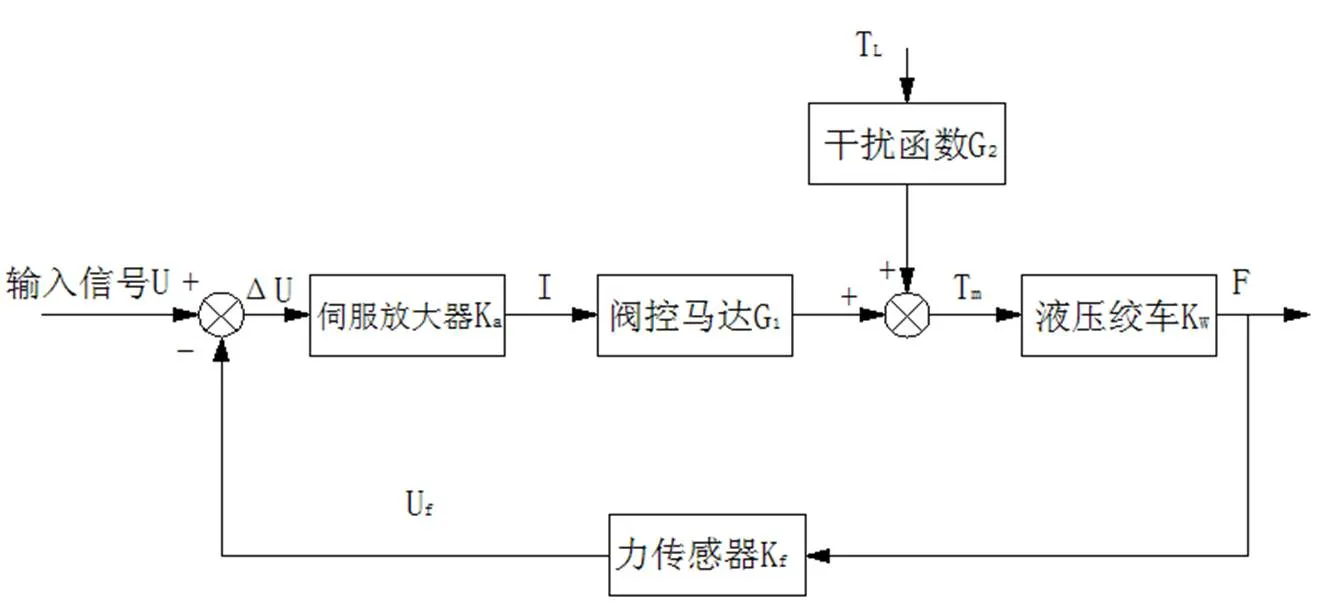
图1 力伺服波浪补偿器的控制过程方框图

Fig.1The block diagram of the control process of Force-servo Heave Compensator

1.2 力伺服波浪补偿器的数学模型参数

力伺服波浪补偿器的数学模型相关参数如表1所示。

表1 力伺服波浪补偿器数学模型相关参数

1.3 伺服阀控马达的数学模型

伺服阀控马达的原理如图2所示，它由四通阀和带有弹性负载、黏性摩擦负载、惯性负载以及任意外加负载力矩的液压马达组成，其动态过程由3个基本方程[6]表示。

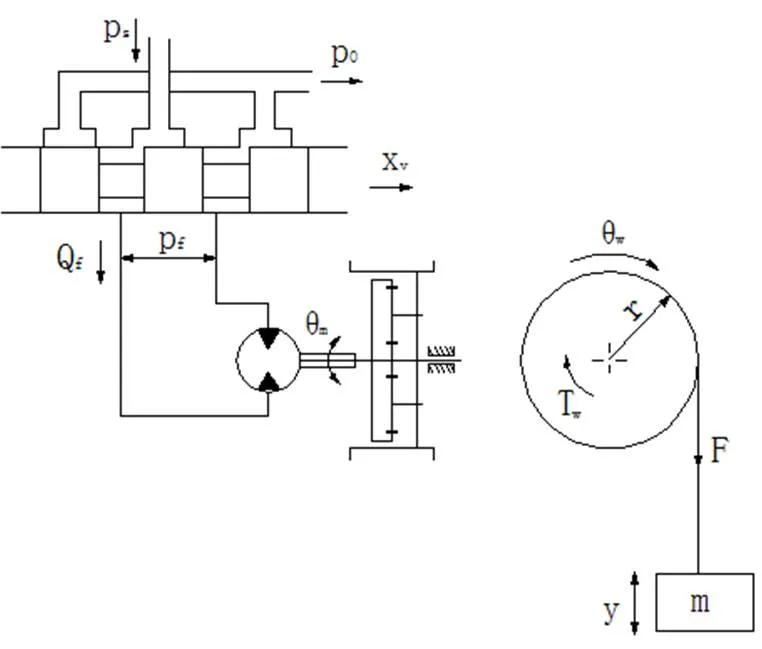
图2 伺服阀控马达的原理图

伺服阀的负载流量方程的拉氏变换式为

伺服阀到液压马达的流量连续方程的拉氏变换式为

(2)

液压马达轴的动力学力矩平衡方程的拉氏变换式为

式(1)、(2)、(3)中

K–伺服阀的流量增益，m3·A-1·s-1；

–伺服阀的控制电流，A；

K–阀的压力系数，m3·s-1·pa-1；

C–马达总泄露系数，m3·s-1·pa-1；

V–马达两腔及连接管道总容量，m3；

B–马达和负载阻力系数，N·m·s-1；

–负载的扭矩弹簧刚度，N·m·rad-1；

T–作用在马达轴上的外负载力矩，N·m；

T–马达的输出力矩，N·m；

J–马达和负载折算到马达输出轴的总惯量，kg·m2；

由式(1)、(2)消去得

由式(3)得

(5)

将式(5)代入式(4)得

由式(6)可知，伺服阀的控制电流和作用在马达轴上的外负载力矩T两个因素影响马达的输出扭矩大小。为了减少或消除作用在马达轴上的外负载力矩的干扰因素，可以运用前馈复合控制方法将作用在马达轴上的外负载力矩干扰因素既按照偏差也按照干扰进行调节，其控制过程方框图如图3所示。

图3 前馈复合控制系统的控制过程方框图

Fig.3 The block diagram of the control process of feed-forward compound control system

由图3可得马达的输出扭矩为

消除作用在马达轴上的外负载力矩的干扰因素，可得消除外负载力矩环节的传递函数为

(8)

消除作用在马达轴上外负载力矩即T=0时，由式(6)可得阀控马达的传递函数为

式(9)中=Js+Bs+

对于阀控液压马达来说，其所受弹性负载很少见，令负载的扭转弹簧刚度系数=0，且，这样阀控马达的传递函数可以大大简化为

式(10)中

，

1.4 阀控马达的外界干扰环节传递函数

假设伺服阀的控制电流=0且令负载的弹簧刚度=0时，由式（6）可得阀控马达的外界干扰环节的传递函数G()为

式(11)中

，

1.5 力伺服波浪补偿器的数学模型

通过复合控制方法[7]消除作用在马达输出轴上的外负载T因素，消除外负载力矩的力伺服波浪补偿器的控制过程方框图如图4所示。

图4 消除外负载力矩的系统的控制过程方框图

由图4可知，力伺服波浪补偿器的开环传递函数为

式(12)中

力伺服波浪补偿器的闭环传递函数为

(13)

将表1中的力伺服波浪补偿器数学模型相关参数值代入式(12)、(13)中，得

(15)

2 力伺服波浪补偿器的控制性能分析

力伺服波浪补偿器的稳定性、能观性、能控性分析，是其控制系统能否正常工作的前提，也是控制系统能否优化的基础[8]。

2.1 力伺服波浪补偿器的状态方程

将中间变量Z引入式(15)中得

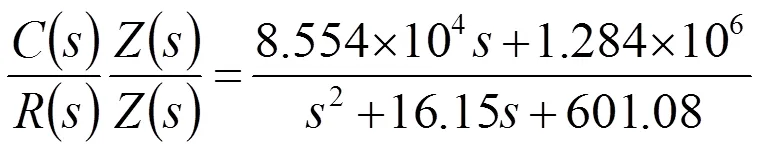
式(16)中

由式(16)可得其微分方程为

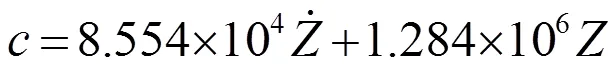
(17)

系统的输出方程为

2.2 力伺服波浪补偿器的稳定性分析

基于Matlab软件，对力伺服波浪补偿器的稳定性进行分析[9]，开环Nyquist曲线如图5所示，曲线不包围（-1，j0），因此系统开环特征方程不稳定的根的个数为0，根据Nyquist稳定判据，其闭环系统稳定。

图5 开环系统的Nyquist曲线

2.3 力伺服波浪补偿器的能观性、能控性分析[10]

满秩即(Q)=。

满秩即(Q)=。

由式(17)、(18)可知力伺服波浪补偿器状态方程和输出方程的系数矩阵A、B、C为

系统状态的能控性判别矩阵的秩为

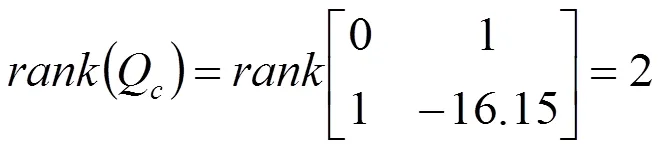
符合系统状态能控性的判别准则要求，因此力伺服液压控制系统具有能控性。

系统状态完全能观测的判别矩阵的秩为

符合系统状态能观测的判别准则要求，因此力伺服液压控制系统具有能观性。

3 力伺服波浪补偿器的控制性能优化

基于Matlab软件，力伺服波浪补偿器的闭环频域图如图6所示，力伺服波浪补偿器的系统带宽为1.21e5。一方面，力伺服波浪补偿器的伺服带宽要受到液压—机械综合谐振的限制，其系统带宽无法达到这一数值；另一方面，在系统的输出量复现输入信号的过程中，会遇到各种干扰信号，系统的带宽过大，无法滤掉高频干扰信号，抑制干扰的能力变差。为均衡动态滞后和噪声干扰，同时考虑液压—机械综合谐振的限制，需要对力伺服波浪补偿器的控制系统极点进行配置[11]，对其控制性能进行优化。

图6 开环系统的Bode图

3.1 极点配置前系统的状态变量图

由式（15）可确确定未优化前的系统状态变量图如图7所示。

图7 未优化前闭环系统的状态变量图

3.2 系统期望极点的确定

根据海上起吊作业的要求，力伺服波浪补偿器的瞬态响应指标[12]为：输出响应的最大超调量M≤5%，峰值时间t≤0.5s。

系统的期望极点为

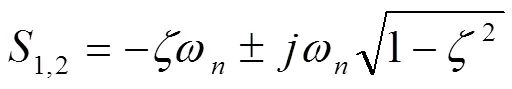
根据力伺服波浪补偿器的瞬态响应指标，可以列出不等式组为

(20)

由不等式组(20)，可得一组解为

将式(21)代入式(19)得系统的期望极点为

(22)

由期望极点构成的特征多项式为

由式(23)可得

，

由式（15）可知受控系统的特征多项式为

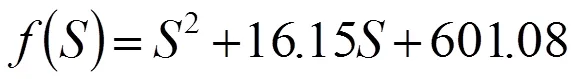
由式(24)可得

，

力伺服波浪补偿器控制系统的状态反馈矩阵K为

为了使力伺服波浪补偿器控制系统的单位阶跃信号的跟踪信号误差e=0，即绳索所受到恒定的拉力。

极点配置后控制系统的闭环传递函数为

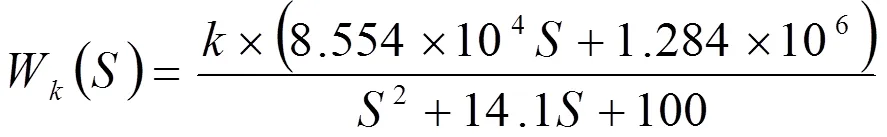
式(26)中—系统的输入放大系数

单位阶跃信号的跟踪信号误差e为

(27)

由式(27)可得

=7.8×10-5

将=7.8×10-5代入式(26)得，极点配置后控制系统的闭环传递函数为

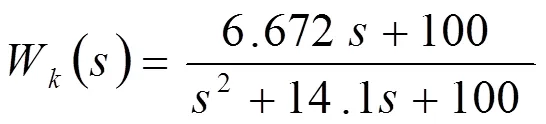
系统进行极点配置后的闭环系统的状态变量图如图8所示。

图8 极点配置后闭环系统的状态变量图

Fig.8 The state variable diagram of the closed-loop system after pole-assignment

优化前后的系统的图如图9所示，优化前系统的带宽为1.21e5 rad/s，优化后系统的带宽为12.4 rad/s。力伺服波浪补偿器的伺服带宽可以达到优化后系统带宽值；另一方面，该系统的带宽适中，可以滤掉高频干扰信号，抑制干扰的能力增强。优化前后的系统数学模型仿真[13-14]如图10所示，对优化前后的系统输入阶跃信号，获得阶跃响应曲线[15]。优化前后的系统的阶跃响应曲线对比图如图11所示，优化后系统的阶跃响应曲线的超调量降低到5%；优化后的系统的峰值时间降低到0.3 s，其单位阶跃信号跟踪信号误差e=0，满足力伺服波浪补偿器的瞬态响应指标的设计要求。

图9 优化前后的系统的Bode图

图10 优化前后的系统的数学模型仿真图

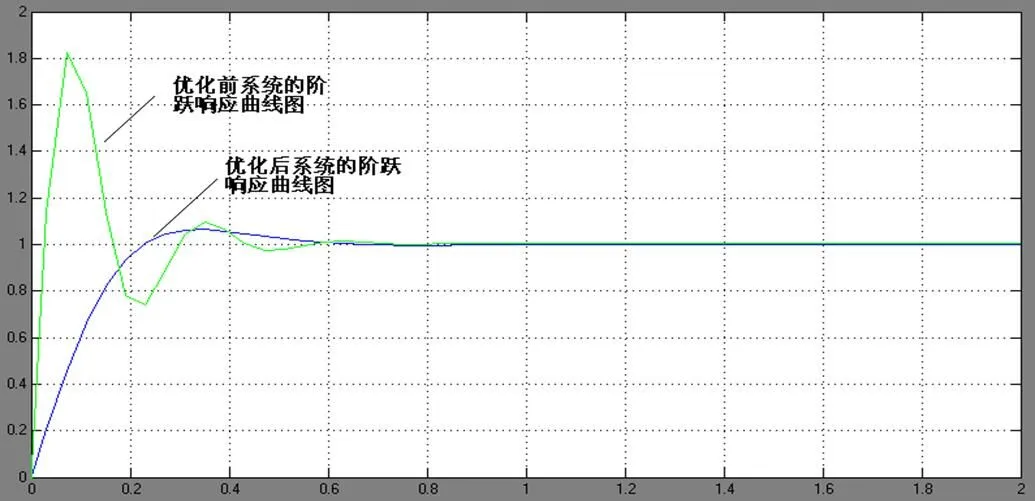
图11 优化前后系统的阶跃响应曲线图

5 结论

(1)本文首先建立力伺服波浪补偿器的数学模型。通过系统的数学模型可以看出影响液压马达的输出扭矩的因素有作用在液压马达的外负载力矩T和伺服阀控制电流两个因素。为了使伺服阀控制电流成为影响液压马达的输出扭矩的唯一影响因素，采用前馈复合控制方法消除作用在液压马达的外负载力矩T这个影响因素。

(2) 对消除作用在液压马达的外负载力矩的力伺服波浪补偿系统的控制性能进行研究，得出系统具有能观能控性，同时具有相对稳定性。

(3) 对系统的控制性能进行优化。由于优化前系统的伺服带宽太大，抑制噪声的能力很差，因此依据力伺服波浪补偿器的控制性能的预定设计指标，对系统进行极点配置，获得误差指标最佳时的状态反馈矩阵和系统放大系数。

(4) 对优化前后的系统进行系统仿真验证，优化后系统的阶跃响应曲线的超调量降低到5%；优化后的系统的峰值时间降低到0.3 s，其单位阶跃信号跟踪信号误差e=0，满足力伺服波浪补偿器的瞬态响应指标的设计要求。本文的研究结果对设计和使用力伺服波浪补偿器的控制系统均具有很强的指导意义和参考价值。

参考文献：

[1] Brian Beasley, Cooper Best, Derek Davis. Design of flying eye remotely operated vehicle for deep water surveillance[J]. IEEE, 2000:2075-2009.

[2] 王志勇, 谌志新, 徐志强. 深水勘测装置波浪补偿系统设计[J]. 机械工程学报, 2013, 11(1)：55-58.

[3] 徐小军, 陈循, 尚建忠. 一种新型主动式波浪补偿系统的原理及数学建模[J]. 国防科技大学学报, 2007, 29(3)：118-122.

[4] 陆卫杰. 船艇并靠导弹补给及波浪补偿系统研究[D]. 南京：南京理工大学, 2006.

[5] 胡永攀, 陈循, 陶利民, 等. 主动式波浪补偿起重机液压伺服系统数学建模及仿真[J]. 机床与液压, 2010, 38(9)：80-84.

[6] 李连升, 刘绍球. 液压伺服理论与实践[M]. 北京：国防工业出版社, 1990：110-116.

[7] 王益群, 孔祥东. 控制工程基础[M]. 北京：机械工业出版社, 2008.

[8] Dorf R C. Modern Control Systems [M]. Menlo Park, CA:Addision Wesley Longman,Inc.1998.

[9] 刘少军. 现代控制方法及计算机辅助设计[M]. 长沙：中南大学出版社, 2003.

[10] 胡寿松. 自动控制原理[M]. 北京：科技出版社, 2001.

[11] 成大先. 液压控制机械设计手册[M]. 北京：化工工业出版社, 2004.

[12] 王占林. 近现代液压控制[M]. 北京：机械工业出版社, 1997.

[13] 韩俊峰, 邹慧君. 机电一体化系软件建模技术与仿真软件的研究与分析[J] . 机械设计与研究, 2003, 19(4)：31-34.

[14] 王东, 黄效国, 过跃. 基于Matlab/Simulink的阀控缸模块化建模与研究[J] . 机床与液压, 2009, 37(9)：240-242.

[15] 黄忠霖,周向明.控制系统Matlab计算与仿真实例[M] . 北京：国防工业大学出版社, 2006.

THE FORCE SERVO HEAVE COMPENSATOR CONTROL PERFORMANCE OPTIMIZATION

*ZHOU Ming-jian1, WANG You-min2

(1. College of Electronic Engineering and Electrical Automation, Chaohu University, Chaohu, Anhui 238000, China;2. College of Mechanical & Automation Engineering, Anhui polytechnic University, Wuhu, Anhui 241000, China)

Force Servo Heave Compensator is widely used in the field of ocean engineering, so the study of the control system of Force Servo Heave Compensator is of great significance. First of all, establish its mathematical model, using feed-forward compound control method to eliminate the disturbance interference that the load torque disturbance acting on the output shaft of the hydraulic motor. Based on the mathematical model of disturbance interference elimination system, analyzes the stability, the observability & the controllability of the system to prepare for the control performance optimization. Then, using pole assignment method to optimize the control performance of the system, get feedback matrix. Finally, the control performance of the optimized system is verified by the simulation, achieving the target of optimization design.

force servo heave compensator；feed-forward compound control；pole assignment method；control performance optimization design

1674-8085(2015)01-0070-07

TH137.5

A

10.3969/j.issn.1674-8085.2015.01.014

2014-07-14；修改日期：2014-09-21

巢湖学院校级产学研专项项目(XLY-201419)

*周明健(1987-)，男，安徽宣城人，助教，主要从事流体机械与传动研究(E-mail：zhoumingjian88@126.com);

王幼民(1964-)，男，安徽芜湖人，教授，硕士，硕士生导师，主要从事流体机械与传动研究(E-mail:wymtlf@126.com).