等效载荷法在高周疲劳寿命分析中的应用

【摘 要】民机设计选材中，高周疲劳寿命是很关键的性能，但高周疲劳试验存在周期长、成本高、试验结果分散性大等特点，为保证最终拟合曲线具有足够高的置信度（95%），使用传统的Smax-logNf形式拟合法，通常需要进行大量试验。在此提出新的基于等效载荷的拟合方式，在不影响置信度水平的前提下，可以使用更少的试样获得寿命曲线，且更有效评定应力或应力比对特定材料疲劳性能的影响，

【关键词】民机选材 高周疲劳 S/N曲线 等效载荷法 Smax-logNf形式

民机设计选材中，高周疲劳寿命是很关键的性能，根据一般经验，使用传统的Smax-logNf形式拟合法获得某一Kt、R参数下的高周疲劳曲线，通常需要进行大量试验。传统方法拟合结果如图1所示，即便将曲线汇总到同一张图表，实际上使用的仍是不同的拟合模型。

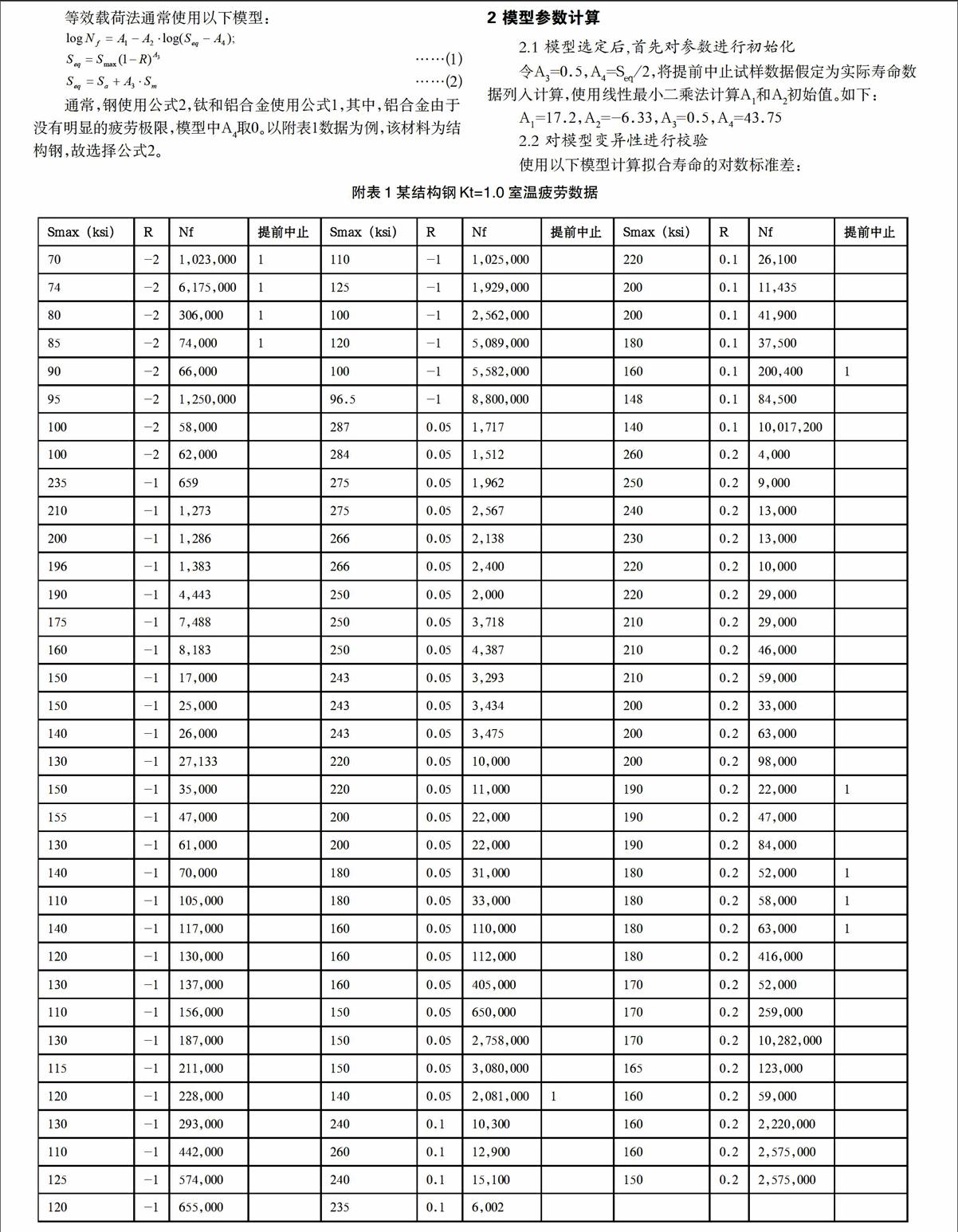
以附表1为例，数据涉及5个不同的应力比R。若使用传统的Smax-logNf形式拟合法，需要分为5个模型进行拟合，且每个应力比所对应的曲线为满足置信度需求，需要大量试验（根据经验，一般不低于45个试样），很明显表格中的数据量不够，不足以生成所需的高周疲劳曲线。

为此，我们使用新的等效载荷法对数据进行分析。将同一类型试样不同应力比的数据作为一个集合，使用统一的数学模型进行分析。该方法有效提高了样本规模，且通过同一模型拟合，直观反映应力比变化对特定材料高周疲劳寿命的影响。如图2所示，针对附表1数据，使用等效载荷法进行拟合，通过一个统一的模型（式中，Seq为等效应力，Sa为根据循环应力曲线计算得到的平均应力，Sm为应力幅。Seq与R相关），仅使用少数试样即获得了5个不同应力比下的高周疲劳曲线。不论从节约试验成本和周期的角度，还是从直观表征应力比对对特定材料高周疲劳寿命影响的角度，该方法都具有极大的实用价值。

图2 某结构钢室温疲劳曲线，Kt=1.0

1模型的选择

等效载荷法通常使用以下模型：

……（1）

……（2）

通常，钢使用公式2，钛和铝合金使用公式1，其中，铝合金由于没有明显的疲劳极限，模型中A4取0。以附表1数据为例，该材料为结构钢，故选择公式2。

2模型参数计算

2.1模型选定后，首先对参数进行初始化

令A3=0.5，A4=Seq/2，将提前中止试样数据假定为实际寿命数据列入计算，使用线性最小二乘法计算A1和A2初始值。如下：

A1=17.2，A2=-6.33，A3=0.5，A4=43.75

2.2对模型变异性进行校验

使用以下模型计算拟合寿命的对数标准差：

；其中，Ri为拟合寿命的对数残差，σ0≥0。

使用上一步获得的A1～A4初始值计算Ri和对应的Seq，再用最小二乘法计算σ0和σ1及对应的90%置信区间。若σ1置信区间上界小于0，则数据可能有误，需要进一步检查；若σ1置信区间包含0（实践中很少出现），则使用无加权模型对模型参数进行估算（也可继续采用下述的加权模型进行分析）；若σ1置信区间下界高于0，则使用加权模型继续对参数进行估算。

此处，σ0拟合值为-0.49，小于0，故将σ0置为0，重新拟合σ1=55.03，其置信区间下届高于0。故，应当使用加权模型继续分析。

2.3使用加权模型进行进一步估算

对模型进行加权调整，各项除以上一步计算获得的对应各项的g（Seq）（注，因各项残差Re不同，故g（Seq）不是常数），如下：

对上述模型进行非线性回归（某些软件，如Minitab可以进行该分析），计算得到A1～A4估计值如下：

A1=14.93；A2=-5.40；A3=0.47；A4=57.58

2.4对模型参数显著性进行校验

对上一步计算获得的A2计算其90%置信区间。若置信区间上界为负，则说明logNf和Seq之间拟合关系显著，否则需要进一步检查数据源。

此处，A2置信区间上界为-3.9955，小于0，所以该模型拟合显著性明显，可以进行下一步分析。

2.5针对加权模型获得的参数进一步进行修正

将上一步获得的A3作为常数，重新计算g（Seq），并针对加权模型再次进行非线性回归，重新估算A1、A2、A4。新的估算值如下：

A1=14.08；A2=-5.07；A3=0.47；A4=63.9

如果可能（有相应的计算软件），还可以用极大似然法再对模型进行一次回归，对提前中止试样的破坏寿命进行估算，从而对模型参数进一步微调，通常使用极大似然法微调将得到稍大的A1和稍低的A2。此处，微调后的A1=14.2，A2=-5.10。

2.6计算拟合模型的标准化残差

标准化残差SRi=Ri/SD，其中：

；

将标准化残差SRi与应力比R作图，如图3所示，若某一应力比所对应的SRi明显偏离中线，则表明该应力比的数据严重偏离，拟合模型显著性不佳。为定量表征这样的拟合不足，可以使用Durbin-Watson校验，使用以下统计量

，若 ，则认为拟合模型拟合不足的显著度大于5%，应重新选择新的拟合模型或去掉相应应力比数据再重新拟合。

此处，D=1.7179，下限为1.6407。因此，可以确定上述模型拟合显著，如下：

图3 标准化残差SRi与应力比R关系图

参考文献：

[1]MMPDS，Metallic Materials PropertiesDevelopment and Standardization

[2]Montgomery， D.C. and Peck， E.A.， Introduction to Linear Regression Analysis， Wiley， New York （1982）

作者简介：陈颖（1983—），男，研究生学历，现任上海飞机设计研究院标准材料设计研究部工程师，主要工作方向为金属材料设计用选材及金属材料设计用许用值统计分析。