求积元法在金融工程计算领域应用初探
2015-11-03杨燕曦
杨燕曦
摘要金融工程领域的大量实际问题最终都可归结为对随机微分方程(组)的求解.针对金融工程计算领域涉及到的静态一维问题,首次将求积元方法应用于非自伴随微分方程的求解.建立了相应的求积元方法计算单元.对典型问题进行计算,并与解析解、有限差分解、有限元解分别进行对比.结果表明,求积元法是一种简单准确高效的数值方法,可进一步用于金融工程计算领域动态问题、二维问题的计算分析.
关键词数理经济;数值方法;求积元法
中图分类号F830.91 文献标识码A
A Preliminary Study on the Application of QEM
in Financial Engineering Analysis
YANG Yanxi
(Party School of the Organ Directly Under the Hunan CPC Provincial Committee, Changsha, Hunan410079, China)
AbstractMany practical problems in modern finance can be cast into the framework of stochastic differential equations. The static 1D problem in financial engineering characterized by nonselfadjoint was examined in this paper by using the Quadrature Element Method (QEM) for the first time. The quadrature element for the problem mentioned above was established, and numerical results from QEM were compared with the analytic solution, FDM and FEM respectively. It is shown that high computational accuracy and efficiency are achieved using QEM, and this method can be further used in dynamic problem, 2D problem of financial engineering.
Key wordsMathematical Economics;Numerical Method;Quadrature Element Method
1引言
随着科学技术的不断发展,在现代金融工程领域愈来愈重视定量的数理分析,大量的实际问题,如动态最优定价、金融衍生产品的定价、投资风险的规避等,经过数理建模,最终都归结为对随机微分方程(组)的求解[1-3].这些微分方程(组)中很多都不易求得解析解,发展相应的数值解法具有重大意义.传统的数值求解方法主要包括二叉树方法,蒙特卡洛方法、有限差分法[4],这些方法对计算机的计算能力要求较低,计算精度不高.近年来,国内外学者又将有限元法应用于金融工程计算领域[5],提高了计算的精度和效率,但其收敛性和稳定性还有待进一步研究.当前,金融活动的风险及复杂性进一步加剧,数理建模得到的微分方程规模更大、复杂程度更高,有的还具有一定的非线性,迫切需要一种简洁、准确、高效的数值计算方法.
求积元方法是一种结合了高效数值积分和微分求积法二者优势的新的求解常(偏)微分方程(组)的
高阶数值方法.该方法自2007年由清华大学钟宏志教授提出以来,在工程结构分析领域中已得到较为广泛地应用[6-9],展现出其相比传统有限元法的独特优势.
工程结构计算分析所涉及的微分方程(组)一般均具有线性自伴随的特性,因而具有相应的变分形式.而对于金融工程计算分析中所涉及的微分方程(组)一般不具有自伴随的特性,对于求积元方法的应用还是一个新的领域.
针对金融工程计算领域的静态一维问题,将求积元方法应用于非自伴随的微分方程的数值求解,建立相应的求积元单元.选取3个典型问题进行计算,与解析解、有限差分解和有限元解分别进行比较,验证求积元方法的适应性、准确性和高效性.为该方法在金融工程计算领域动态问题(期权定价问题)、二维问题中的深入应用奠定基础.
2一维边值问题的求积元离散
一般地,金融工程中的静态一维问题可用如下微分方程
u″(x)+a1(x)u′(x)+a2(x)u(x)+f(x)=0(1)
和相应的边界条件表示,
α1u(xmin)+β1u′(xmin)=γ1,(2)
α2u(xmax)+β2u′(xmax)=γ2.(3)
式(1)中,ux为定义在区域xmin,xmax上的未知(待求)函数,u″x、u′x分别表示对x求二阶、一阶导数.a1x、a2x、fx为已知函数.式(2)、式(3)为边界条件.
假设未知函数ux可以用近似函数x来表示,基于Galerkin加权残值积分近似为零和求积元法求解思想,权函数选定为近似函数的变分δ,令式(1)残值在加权积分意义下为零,即
∫xmaxxminδ″+a1′+a2+fdx=0.(4)
对式(4)中的二阶导数进行分部积分
∫xmaxxminδ″+a1′+a2+fdx
=′δxmaxxmin-∫xmaxxmin′δ′dx
+∫xmaxxminδa1′+a2+fdxendprint
=∫xmaxxmin-′δ′+a1′δ+a2δ+fδdx
+b.t.=0.(5)
式(5)中,b.t.表示边界条件.
将式(5)中积分进一步离散,根据求积元求解基本步骤,首先将待求解物理域坐标系通过式(6)转换到标准域,如图1所示,图中1,2,3,…,N-1,N为Lobatto数值积分[10]点.
ξ=2Lx-xmin-1,ξ∈-1,1;L=xmax-xmin.(6)
利用Lobatto数值积分[10]计算式(5)中的积分,
∫xmaxxmin-′δ′+a1′δ+a2δ+fδdx=∫1-1-′δu′2/L2+a1′δ2/L+a2δ+fδdξL2=∑Ni=1Hi-′δu′2/L2+a1′δ2/L+a2δ+fδiL2.(7)
其中,N表示积分点数,右侧下标i表示该变量在积分点处的值,Hi为相应积分点对应的积分权系数.需指出,式(7)中导数′均为对标准域坐标ξ求导.结合微分求积法则[11],
dmfdξmξ=ξi=∑Nj=1Cmijfξj.(8)
将式(7)中所含积分点处的函数值和函数导数值表示为积分点处基本自由度(近似函数值i)的线性加权代数和.式(8)中,Cmij为m阶微分求积系数.
物理域坐标系下Lobatto数值积分点处i组成的列向量构成了待求解问题的单元基本自由度,
e=1…i…NT,i=1,…,N.(9)
e右上角(e)即表示一个求积元单元,则
′i=B1ie,′i=B0ie.
(10)
式(10)中,
B1i=C11j…C1ij…C1Nj,j=1,…,NB0i=δ1j…δij…δNj,j=1,…,N.(11)
其中δij为Kronecker符号,即
δij1, i=j;0, i≠j.(12)
则式(7)可进一步表示为
∑Ni=1Hi-′δ′2/L2+a1′δ2/L+a2δ+fδiL2=δeT∑Ni=1Hi-BT1iB1i2/L2+a1iBT0iB1i2/L+a2iBT0iB0iL2e+δeT∑Ni=1HiBT0ifiL2=-δeTKee+δeTFe.
(13)
则式(13)中
Ke=∑Ni=1HiBT1iB1i2/L2-a1iBT0iB1i2/L-a2iBT0iB0iL2Fe=∑Ni=1HifiL2,
(14)
则式(5)最终离散为
∫xmaxxminδ″+a1′+a2+fdx
=-δeTKee+δeTFe
+b.t.=0.(15)
由于变分δe具有任意性,式(15)可转化为一个线性代数方程组,
Kee=F(e).
(16)
对于边界条件b.t.,当β1≠0且β2≠0时,边界条件可表示为
b.t.=′δxmaxxmin=δNγ2-α2Nβ2-δ1γ1-α11β1.
(17)
可对矩阵Ke、Fe修正如下:
K^e11=Ke11+-α1β1,K^eNN=KeNN+α2β2F^e1=Fe1+-γ1β1,F^eN=FeN+γ2β2.(18)
K
Euclid ExtrazB@ e、F
Euclid ExtrazB@ e其余元素分别与Ke、Fe一致,则式(16)转化为
K^ee=F^e
(19)
进行求解.
当β1=0且β2=0时,边界条件可表示为
b.t.=′δxmaxxmin=δN′N-δ1′1(20)
由于β1=0且β2=0,由式(2)和(3)可知,u1、uN为常量,
u1=1=γ1α1,uN=N=γ2α2,(21)
则
δ1=δN=0.(22)
只需修正Ke、Fe,使其满足式(21)即可.故修正如下:
(e)11=1,(e)1j=0,j=2,…,N;
(e)NN=1,(e)Nj=0,j=1,…,N-1;
(e)=γ1α1,(e)N=γ2α2.(23)
K
Euclid ExtrazB@ e、F
Euclid ExtrazB@ e其余元素分别与Ke、Fe,则式(15)仍转化为
K^(e)(e)=F^(e)
(24)
进行求解.其余边界条件,如β1≠0而β2=0,亦可类似处理.
求解代数方程组,即可得e中各元素,物理域中非Lobatto数值积分点处的函数值可通过对i进行拉格朗日插值得到.需要说明的是,对于一般性问题求积元方法仅需在待求解域上划分一个单元.同时,也可视问题需要进行多个单元拼接求解.有关求积元法的详细介绍可参考相关文献[6-9].
3实证分析
选取金融工程计算分析中较为典型的3个实例,采用求积元方法进行计算,验证求积元方法的准确性和高效性.计算程序采用Matlab软件编制.
3.1垄断动态最优化问题
垄断企业的目标是寻找产品价格P的一条最优路径,从而在一个有限的时间内[0,T]内实现利润最大化.假设这个时期足够短,以保证固定的需求成本函数以及忽略折现的设定是合理的.这个问题可以通过变分法采用一个欧拉方程来描述[12],
P″-b(1+αb)αhP=-a+2αab+βb2αh2,endprint
P(0)=P0,P(T)=PT.
(25)
该方程是一个二阶线性微分方程,其解析解为
P=A1ert+A2e-rt+P,
r=b(1+αb)αh2,P=a+2αab+βb2b(1+αb).(26)
将边值条件代入式(26),可得
A1=P0-P-(PT-P)erT1-e2rT,
A2=P0-P-(PT-P)e-rT1-e-2rT.(27)
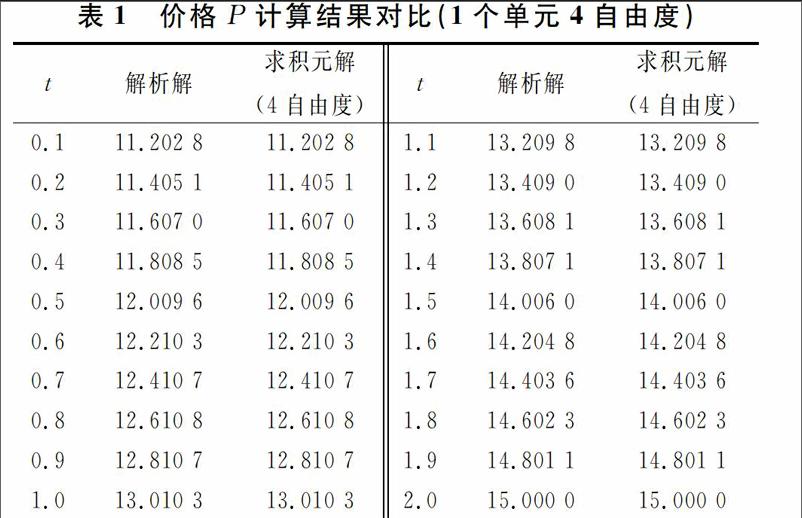
应用求积元方法对该问题在t=[0,2]定义域内进行求解,各时刻t价格P的计算结果与解析解的对比如表1所示.计算相关参数:产出函数中的系数,a=160,b=8,h=100;总成本函数中的系数,α=0.1,β=100;P0=11,PT=15.由表1可见求积元方法仅需划分1个求积元单元4个积分点(N=4)共计4个自由度即可达到良好的求解精度,小数点后4位有效数字与解析解完全一致,体现出求积元方法的准确性.
3.2几何布朗运动的首出时
考察几何布朗运动
dY=aYdt+σYdX
.(28)
在给定标的物价格范围内的首出时是有实践意义的.可以得到给定标的物价格偏离某一确定界限的平均时间,进而评估相关双障碍期权的风险.该问题可以描述为
axu'+σ22x2u''=-1,u(xmin)=0,u(xmax)=0.
(29)
该方程的解析解为
u(x)=1σ2/2-a(ln(xxmin)-1-(x/xmin)1-2a/σ21-(xmax/xmin)1-2a/σ2ln(xminxmax)).(29)
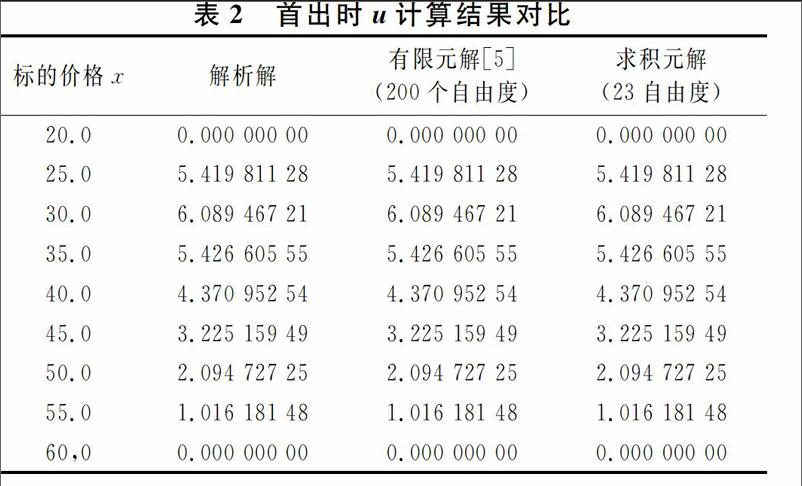
应用求积元方法对该问题进行求解,计算结果与解析解及有限元解[5]的对比如表2所示.计算相关参数为收益率a=0.1,波动率σ=0.2,xmin =20,xmax =60.由表2可见求积元仅需划分1个单元23个积分点共计23个自由度即可达到良好的求解精度,小数点后8位有效数字与解析解完全一致,而有限元法则需要划分99个单元共计200个自由度才能达到以上精度,求积元法的计算自由度仅约为有限元法的十分之一,而计算大规模问题时,计算自由度是影响计算机计算效率的重要因素.因此.求积元法相比有限元法具有更为高效的特点.
3.3对流占优问题
对流占优问题在金融工程中具有很强的实际意义[13],比如当标的物价格较低且(/或)波动率较低时,股票期权、外汇期权的定价将成为对流占优问题.以如下的边值问题
-ku″+u′=0,u(0)=0,u(1)=1.
(30)
为例进行说明,当k减小时,该微分方程椭圆型方程特征逐渐减弱,双曲型方程特征逐渐增强.此时,由于“对流项”u′主要影响方程的特性,该问题称为对流占优问题.
该方程的解析解为
u(x)=1-e(x/k)1-e(1/k).
.(31)
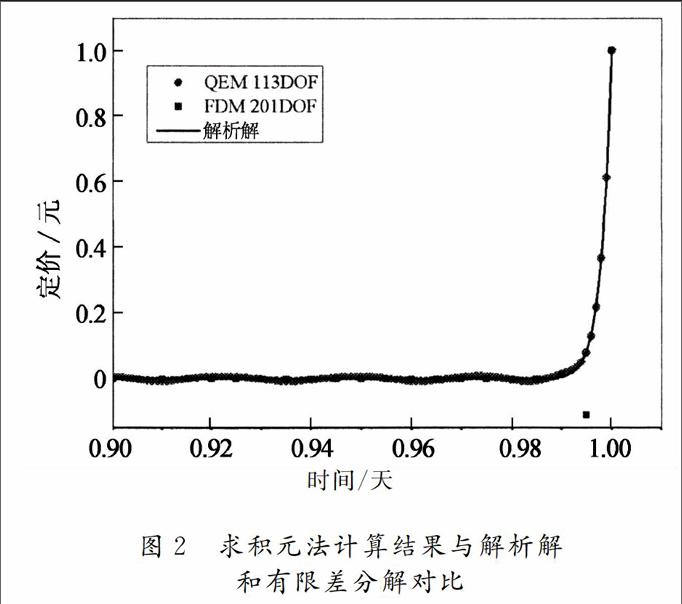
应用求积元方法对该问题进行求解,计算结果与解析解及有限差分解的对比如图2所示.计算相关参数为k=0.002.由图2可见,该问题的解析解曲线具有很强的非线性,表现为在[0,0.99]范围内非常平缓,而在[0.99,1]范围内急剧上升.
本例中求积元方法(QEM)共划分8个单元,每个单元采用15个积分点,共计113个自由度,达到了较好的计算结果.而有限差分法(FDM)在划分单元数较少时,计算结果出现了明显的震荡[5],即使划分200个单元(201个自由度),也存在震荡现象(如图2所示).若采用有限元方法,得到满意的计算结果也需要200个自由度以上[5].相比有限差分法和有限元法,求积元法的计算自由度缩减了近一半,再次体现出准确高效的特点.
4结论
针对金融工程计算领域的静态一维问题,将求积元方法的应用领域从线性自伴随微分方程的求解拓展到非自伴随微分方程的求解.首先,基于Galerkin加权残值法思想建立了相应的求积元单元;之后,选取了三个典型问题进行编程求解计算,并与解析解、有限差分解和有限元解分别进行了比较.
计算结果表明,相比有限元方法和有限差分法,求积元方法在得到相同精度计算结果的同时,大幅减少了自由度数,提高了计算效率.对于一般性问题,仅需划分一个单元,也可视问题的复杂性进行多单元拼接求解.是一种准确、高效和灵活的数值方法.用于金融工程领域的静态一维问题计算分析有较大的优势,可进一步用于该领域动态问题(期权定价问题)、二维问题的计算分析.
参考文献
[1]M ROSS. An Elementary Introduction to Mathematical Finance.[M]. London: Cambridge University Press, 2011.
[2]郭宇权. 金融衍生产品数学模型[M].北京: 世界图书出版公司北京公司, 2010.
[3]科森多尔. 随机微分方程[M]. 北京: 世界图书出版公司北京公司, 2006.
[4]蒋致远, 张跳, 龚闪闪. 基于拉普拉斯变换有限差分方法的B-S期权定价[J]. 经济数学,2014, 31(3): 18-22.
[5]T JURGEN. Financial engineering with finite elements[M]. Chichester: John Wiley & Sons Ltd, 2005.
[6]H ZHONG, T YU. A weak form quadrature element method for plane elasticity problems[J]. Applied Mathematical Modelling, 2009, 33(10): 3801-3814.
[7]H ZHONG, M GAO. Quadrature element analysis of planar frameworks[J]. Archive of Applied Mechanics, 2010, 80(12): 1391-1405.
[8]Z SHEN, H ZHONG. Static and vibrational analysis of partially composite beams using the weakform quadrature element method[J]. Mathematical Problems in Engineering, Vol. 2012, Article ID 974023, 23 pages.
[9]Z SHEN, H ZHONG. Nonlinear quadrature element analysis of composite beams with partial interaction. Australian Journal of Mechanical Engineering, 2013, 11(1): 45-52.
[10]P DAVIS, P RABINOWITZ. Methods of numerical integration. [M]. Orlando: Academic Press, 1984.
[11]C SHU. Differential quadrature and its application in engineering[M]. London: SpringerVerlag, 2000.
[12]A CHIANG. Elements of Dynamic Optimization [M]. New York: McGrawHill, Inc,1992.
[13]R SEYDEL. Tools for Computational Finance [M]. Berlin: Springer, 2002.endprint
