基于新陈代谢组合模型的装备故障预测*

2015-11-03邵延君潘宏侠马春茂刘永姜

振动、测试与诊断 2015年2期

关键词：预测值灰色线性

邵延君，潘宏侠，马春茂，刘永姜

（1.中北大学机械工程与自动化学院太原，030051）（2.西北机电工程研究所咸阳，712099）

基于新陈代谢组合模型的装备故障预测*

邵延君1，潘宏侠1，马春茂2，刘永姜1

（1.中北大学机械工程与自动化学院太原，030051）（2.西北机电工程研究所咸阳，712099）

针对武器装备故障预测的难点，在灰色GM（1，1）模型和线性回归模型的基础上结合有效度原理建立新的组合模型，该模型是两种模型的拟合。通过对等时距测量的原始数据进行模拟和预测，来估计系统何时达到故障数据的上限，依此来推断系统的故障时间，同时引入新陈代谢法来提高此种方法的预测精度。最后以某型雷达发射机的输出电压数据为例，验证此种模型在故障预测中的有效性和实用性。

灰色线性回归组合模型；故障预测；新陈代谢模型；有效度

引言

雷达作为军队战斗力生成的重要组成部分，是收集各种军事情报、保持、恢复和提高战斗力的重要因素，一旦发生故障或者损坏，将对战争造成巨大的影响。现代雷达系统变得越来越复杂，性能也越来越精密，在获取雷达的特征参数时存在着不确定性和不完整性［1-3］。传统的维修方式（事后维修、定期维修等）已经不能满足现代雷达发展的需求，因此，开展装备的状态的维修应运而生［4］。它可以对装备进行适时适度的可控维修，对降低维修保障费用，提高战备完好率和任务成功率具有重要的意义。而故障预测又是状态维修中最关键的技术之一，因而国内外的很多学者在这方面展开了大量的学术研究，故障预测的方法可分为神经网络预测法、时间序列预测法、回归分析预测法、灰色预测法等［5-9］。灰色预测模型是基于时间预测方法中的一种，它在预测“小样本”、“贫信息”和“不确定性”等问题方面比较有效，它根据已经获得的系统过去和现在的变化状态，结合趋势分析，依据系统预报故障的阈值，估计系统将来是否会发生故障。但最基本的灰色GM（1，1）预测模型存在许多不足，为了提高该模型的预测精度和实用性，很多学者相继提出了多种改进的灰色预测模型［10-14］。在灰色GM（1，1）模型和线性回归模型的基础上，笔者结合有效度原理建立了新的灰色线性回归组合模型，并在灰色线性回归组合模型基础上建立新陈代谢模型，对某型雷达系统的未来状态进行了预测，并对预测结果进行了分析。

1 模型的建立

1.1灰色GM（1，1）模型

设X（0）为非负原始序列，X（0）=（x（0）（1），x（0）（2），x（0）（3），…，x（0）（i），x（0）（n）），对X（0）进行一次累加生成，得到新的数据列X（1）=（x（1）（1），x（1）（2），x（1）（3），…，x（1）（n））。其中

对生成的序列X（1）（t）有如下一阶线性白化微分方程d x（1）/d t+ax（1）=b，当t取单位时间时，一阶微分方程的差分形式等于微分形式，d x（1）/d t=x（1）（t+1）-x（1）（t）=x（0）（t），所以GM（1，1）模型的微分方程可以表示为：x（0）（t）+ax（1）（t）=b，称为GM（1，1）模型的原始形式。

为了使累加生成序列更平滑，对X（1）作紧邻均值生成。Z（1）=（z（1）（2），z（1）（3），z（1）（4），…，z（1）（n）），其中z（1）（t）=0.5（x（1）（t）+x（1）（t-1）），x（0）（t）+az（1）（t）=b为GM（1，1）模型的基本形式。其中：a为发展系数；b为灰作用量；Z（1）为X（1）的紧邻均值生成序列。

对GM（1，1）模型的基本形式的参数a，b进行求解。a和b的数值通过最小二乘法估计得到。

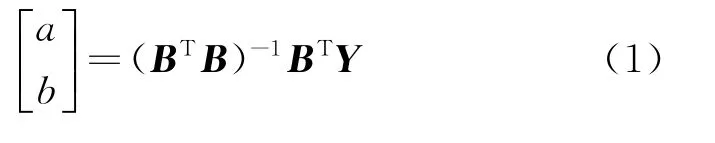
1.2线性回归模型

回归分析是研究一个随机变量Y对另一个（X）或一组（X1，X2，…，Xk）变量的相依关系的统计分析方法。寻找并建立雷达发射机的高压电源电路输出电压与测量次数之间的相关关系模型。然后根据测量次数这个自变量的未来值来预测高压电源电路输出电压值。建立回归模型如下：

其中：t为测量序号；X（t）为电压值；α，β为回归系数。

1.3基于有效度原理建立灰色线性回归模型

将文献［15］提出的基于有效度原理的组合加权系数确定方法引入到灰色模型和线性回归模型中，建立灰色线性回归模型，用来模拟和预测输出的电压值，其建模的思路如下：

设原始数据总数为N，xt为所测电压的实际值为模型的模拟值和精度序列，E和σ分别为序列精度的均值和均方差，其表达式为

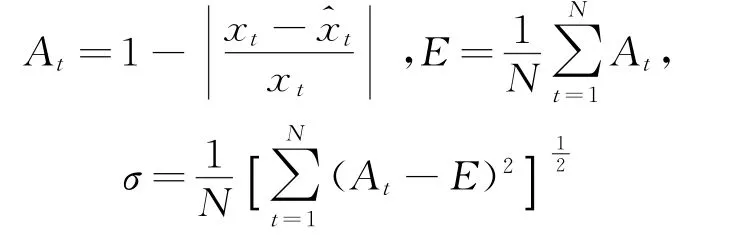
确定模型的有效度

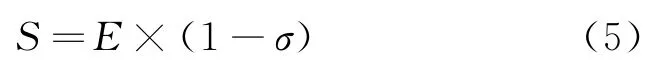
设灰色模型和线性回归模型的有效度分别为S1，S2，加权系数分别为f1和f2。

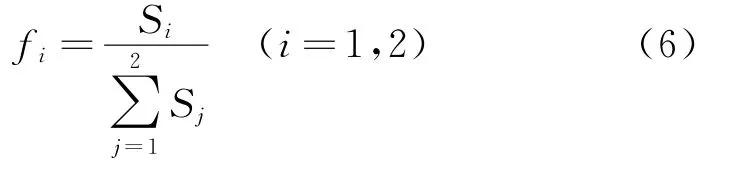
则灰色线性回归模型为

1.4建立新陈代谢模型

为了提高灰色线性回归模型的预测精度，在该组合模型的基础上建立新陈代谢模型，因为在任何一个系统的发展过程中，随着时间的推移，将会不断地有一些随机扰动因素或者驱动因素进入系统，使系统的发展相继受其影响。一般来说，越往未来发展，越是远离时间原点，利用原来的数据对系统的预测的准确性就越差。所以在实际应用中，必须随时将每一个新进入系统的数据置入到建模序列中来，同时把老的信息替换掉，这也就实现了数据的新陈代谢，用动态的新陈代谢模型对系统的未来发展进行动态预测，其建模的思路同第1、3节。

则基于灰色线性回归模型的新陈代谢模型为

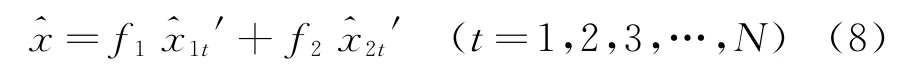
2 实例分析

雷达发射机是雷达系统中造价最昂贵的部位，是为雷达提供大功率射频信号的无线电装置，对其进行故障预测从而进行状态维修具有极其重要的意义。如果雷达发射机输出高压因某种因素发生变化，高压输出超过25 k V的阀值时，就需要进行调整，从而控制输出高压以达到稳压效果，避免发生故障。对某航空维修厂的某型雷达发射机输出高压进行采样得到的一组波纹电压数据，采样采用等间隔采集，每隔50 h采集一次，如表1所示。

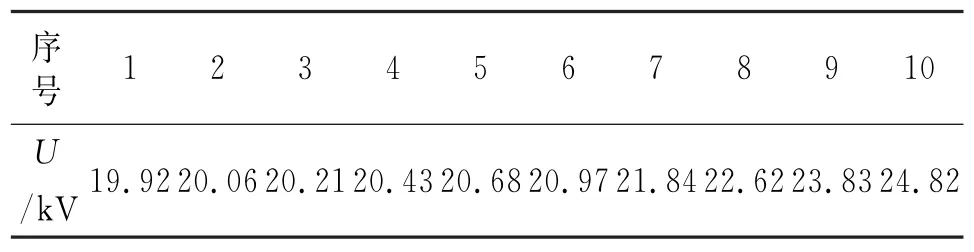
表1　输出高压的原始数据Tab.1 the original data of output voltage

2.1灰色模型预测值

以表1中提供的输出高压的采样数据的前6个数据作为原始序列，最后4个数据作为预测使用，建立GM（1，1）模型，将原始数据进行一次累加生成和紧邻均值生成后，代入式（1）得到B和Y的值。

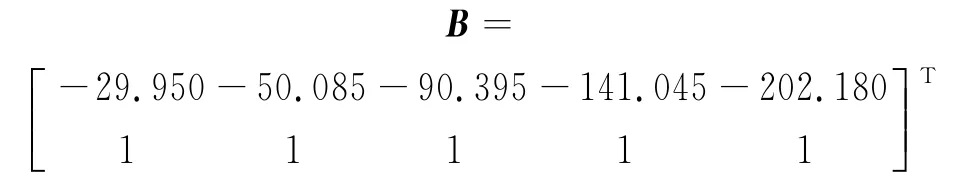
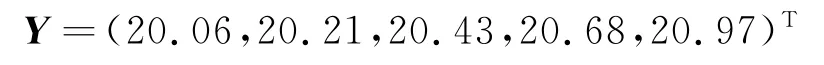
利用Matlab软件，带入B和Y计算，可以得到a和b的值为：a=-0.005 200 7，b=19.935 9，将a和b的值代入时间响应函数（2），则

利用式（3）做累减还原得到GM（1，1）模型对原始序列的模拟值：

同时可得到（x（0）（7），x（0）（8），x（0）（9），x（0）（10））的预测值为

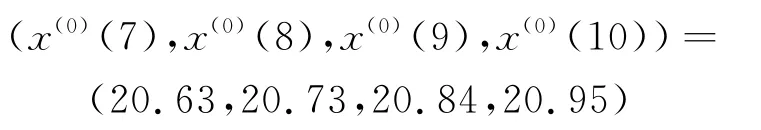
2.2线性回归模型预测值

同样利用表1的前6个数据作为原始序列，最后4个数据作为预测使用，建立线性回归模型。利用最小二乘法求得线性回归方程（2）的参数α和β的值为：α=0.209；β=19.645，将其代入式（3）得到线性回归方程为

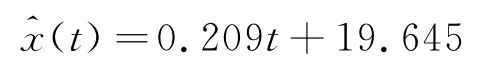
得到线性回归模型对原始序列的模拟值：

同时可得到（x（0）（7），x（0）（8），x（0）（9），x（0）（10））的预测值为

2.3基于有效度原理的灰色线性回归模型的预测值

根据灰色模型与线性回归模型所得出的电压的模拟值与实际值可以计算出E和σ的值，根据式（5）来分别计算灰色模型和线性回归模型的有效度。

（1）灰色模型的序列精度的均值E= 0.991 977，均方差σ=0.015 264 7。则灰色模型的有效度为

（2）线性回归模型的序列精度的均值E= 0.993 699，均方差σ=0.011 346 4。则线性回归模型的有效度为

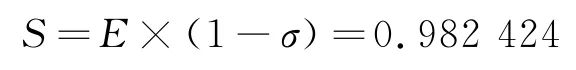
根据灰色模型和线性回归模型的有效度，根据式（6）来分别计算灰色模型和线性回归模型的加权系数，灰色模型的加权系数f1=0.485，线性回归模型的加权系数f2=0.515。则组合模型（7）为

可得到（x（0）（7），x（0）（8），x（0）（9），x（0）（10））的预测值为

2.4新陈代谢模型预测值

当系统置入一个新信息x（0）（7））后，将x（0）（1）去掉，仍然利用灰色线性回归组合模型对6组测量的数据进行模拟，根据2.1～2.3节的计算步骤，则可以得到3种模型的具体形式，如表2所示。

表2　新陈代谢模型Tab.2　Metabolism model

新陈代谢灰色模型的预测值为

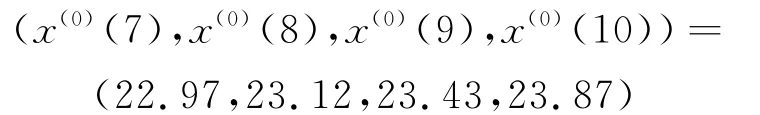
新陈代谢线性回归模型的预测值为

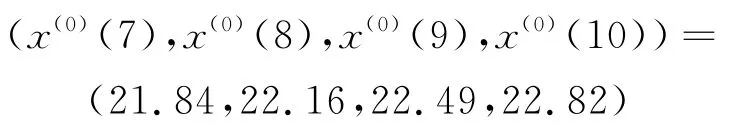
新陈代谢灰色线性回归模型的预测值为

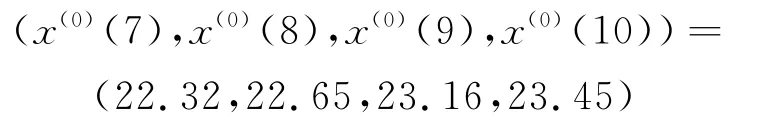
2.5对4种模型得到的电压预测值进行分析

对线性回归模型、灰色模型、灰色线性回归模型和新陈代谢模型得到的预测值和实际值进行误差分析，预测值和实际值的误差分析如表3所示。

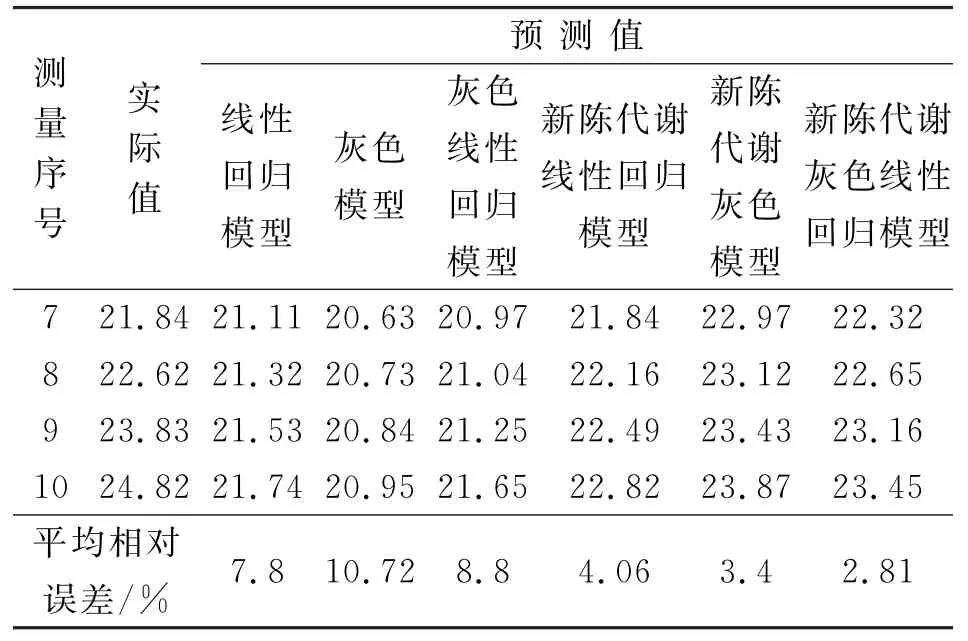
表3　误差分析Tab.3 Error analysis

对上述原模型和新陈代谢模型的预测结果进行误差分析可知，由于在预测的过程中引入了新陈代谢算法，不断的将老信息去掉，置入新采集到的信息，使得预测精度明显高于原模型，结果更为准确，使回归模型的平均相对误差减小了3.74％，灰色模型平均相对误差减小了7.32％，灰色线性回归模型平均相对误差减小了5.99％。

3 结束语

利用有效度原理将线性模型和灰色模型进行拟合，建立的新的灰色线性回归组合预测模型，并结合新陈代谢法不断对预测模型的参数进行调整，使得整个预测模型一直处于更新和发展的过程中。利用新陈代谢预测模型对雷达发射机输出电压数据进行模拟和预测，结果表明，新陈代谢组合模型在预测精度上有显著提高，能够比较准确地对装备进行故障预测，对预防性维修有一定的指导意义，具有一定的实用性。

［1］张光轶，苏艳琴，许爱强.灰色模型在装备故障预测中应用分析［J］.测控技术，2012，31（2）：20-22. Zhang Guangyi，Su Yanqin，Xu Aiqiang.Application analysis of equipment fault prediction based on grey system model［J］.Measurement and Control Technology，2012，31（2）：20-22.（in Chinese）

［2］徐宗昌.装备保障性工程与管理［M］.北京：国防工业出版社，2006：5-20.

［3］许绍杰，谭贤四，王晗中.基于多因素不等时距灰色模型的雷达故障预测［J］.现代雷达，2011，33（8）：25-28. Xu Shaojie，Tan Xiansi，Wang Hanzhong.A MUGM（1，m，w）model of radar fault prediction［J］.Modern Radar，2011，33（8）：25-28.（in Chinese）

［4］武兵，林健，熊晓燕.基于支持向量回归的多参数设备故障预测方法［J］.振动、测试与诊断，2012，32（5）：791-795. Wu Bing，Lin Jian，Xiong Xiaoyan.Method of mechanical equipment fault prognosis based on multi-parameter support vector regression［J］.Journal of Vibration，Measurement&Diagnosis，2012，32（5）：791-795.（in Chinese）

［5］周俊杰，王德功，常硕.基于改进GM（1，1）模型的雷达故障预测［J］.装备维修技术，2010，35（3）：16-18. Zhou Junjie，Wang Degong，Chang Suo.Research on fault prediction of radar based on improved GM（1，1）model［J］.Technology of Equipment Maintenance，2010，35（3）：16-18.（in Chinese）

［6］史佩，高山，苏艳琴.一种改进的GM（1，1）模在装备故障预测中应用［J］.计算机测量与控制，2012，20（5）：1176-1178. Shi Pei，Gao Shan，Su Yanqin.Application analysis of improved GM（1，1）model in equipment fault prediction［J］.Computer Measurement&Control，2012，20（5）：1176-1178.（in Chinese）

［7］黄大荣，黄丽芬.灰色系统理论在故障预测中的应用现状及其发展趋势［J］.火炮发射与控制学报，2009，33（3）：88-92. Huang Darong，Huang Lifen.Present situation and development tendency of grey system theory in fault forecast application［J］.Journal of Gun Launch& Control，2009，33（3）：88-92.（in Chinese）

［8］ Muller A，Suhner M C，Iung B.Formalisation of a new prognosis model for supporting proactive maintenance Implementation on industrial system［J］.Reliability Engineering and System Safety，2008，93（2）：234-253.

［9］ Langseth H，Portinale L.Bayesian networks in reliability［J］.Reliability Engineering and System Safety，2007，92（1）：92-108.

［10］周国雄，吴敏.基于改进的灰色预测的模糊神经网络控制［J］.系统仿真学报，2010，22（10）：2333-2336. Zhou Guoxiong，Wu Min.Fuzzy neural network controlbased on improved gray prediction［J］.Journal of System Simulation，2010，22（10）：2333-2336.（in Chinese）

［11］王晗中，杨江平，黄美荣，等.一种改进不等间距灰色预测模型［J］.空军工程大学学报：自然科学版，2010，11（6）：75-79. Wang Hanzhong，Yang Jiangping，Huang Meirong，et al.Anamendatory unequal interval grey prediction model［J］.Jour-nal of Air Force Engineering University：Natural Science Edition，2010，11（6）：75-79.（in Chinese）

［12］李小力，李言俊，张科.改进的灰色预测模型在导弹中的应用［J］.计算机仿真，2010，27（8）：33-37. Li Xiaoli，Li Yanjun，Zhang Ke.Improved grey forecasting model of fault prediction in missile applications［J］.Computer Simulation，2010，27（8）：33-37.（in Chinese）

［13］刘思峰，郭天榜，党耀国，等.灰色系统理论及其应用［M］.北京：科学出版社，2010：182-187.

［14］陈淑燕，王炜.交通量的灰色神经网络预测方法［J］.东南大学学报：自然科学版，2004，34（4）：541-544. Chen Shuyan，Wang Wei.Grey neural network forecasting for traffic flow［J］.Journal of Southeast University：Natural Science Edition，2004，34（4）：541-544.（in Chinese）

［15］王明涛.确定组合预测权系数最优近似解的方法研究［J］.系统工程理论与实践，2000，20（3）：104-109. Wang Mingtao.Study on method of calculating optimal approximate solution about weight coefficients of combined forecasting methods［J］.Systems Engineering-Theory&Practice，2000，20（3）：104-109.（in Chinese）