基于残留高度球刀铣削粗糙度建模及参数优化*
2015-11-03肖军民
肖军民
(中山职业技术学院机电系,广东中山 528404)
基于残留高度球刀铣削粗糙度建模及参数优化*
肖军民
(中山职业技术学院机电系,广东中山 528404)
基于P20模具钢数控球刀铣削试验,对表面粗糙度的影响因素进行了研究。在试验数据极差分析的基础上得出了如下结论:加工残留高度是球刀铣削粗糙度最重要的影响因素。基于试验数据,利用最小二乘多元线性回归方法,推导并求解出P20模具钢球刀铣削粗糙度的数学模型。利用最优化设计方法和MATLAB优化工具箱,以加工效率为目标函数和以粗糙度预测模型为约束条件,针对实际的问题优选了铣削工艺参数。优化的工艺参数在保证表面加工质量的基础上可大幅提高加工效率,这为数控加工企业降低生产成本提供了重要的理论依据和案例参考。
高速铣削;残留高度;数控加工;表面粗糙度
0 引言
随着数控加工技术的发展和越来越激烈的市场竞争,对产品加工质量和加工效率有着越来越高的要求。在满足产品数控加工质量的前提下提高加工效率是今后数控领域内研究的一个重要方向,而数控切削参数的合理选取则是产品加工质量和加工效率的基本保障。在不同的表面粗糙度技术要求下,研究数控切削参数的优化组合将有着重要意义:它将能够在未实际加工前就可较合理地选定各加工参数,省去试切法的反复试验,在大量减少试制工作的基础上还可以选择加工效率最大的优化参数,这将极大提高企业生产效率。
1 试验条件和测试方法
1.1 试件条件
试验用的工件材料为进口塑料模具钢,牌号为P20,对应中国标准钢号3Cr2Mo。P20的硬度为HRC36-40。数控机床采用德国DMG公司生产的五轴联动加工中心,型号为DMU 60 MONOBLOCK。该五轴联动加工中心为主轴摆动结构,最高转速可达24000r/min。数控铣削刀具采用OSK系列整体式硬质合金球头铣刀,铣刀齿数为2,刀具直径为10mm,刀刃长度为25mm,刀体总长为100mm。
1.2 测试方法
在进行切削加工后测量试件的表面粗糙度,由于其测量具有不确定性,为减少测量误差,在此采用3次测量取平均值的方式。分别在试件3个标记处测量表面粗糙度,以3次测量的平均值作为该次加工后试件表面粗糙度的评定结果。
2 试验设计及数据分析
2.1 试验设计
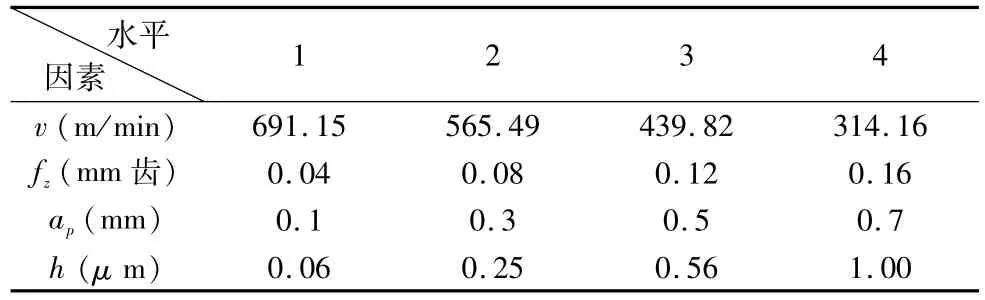
表1 试验因素和水平选取表
2.2 试验数据及分析
依据文献[8]的切削试验,可以获得表2所示的正交试验数据。
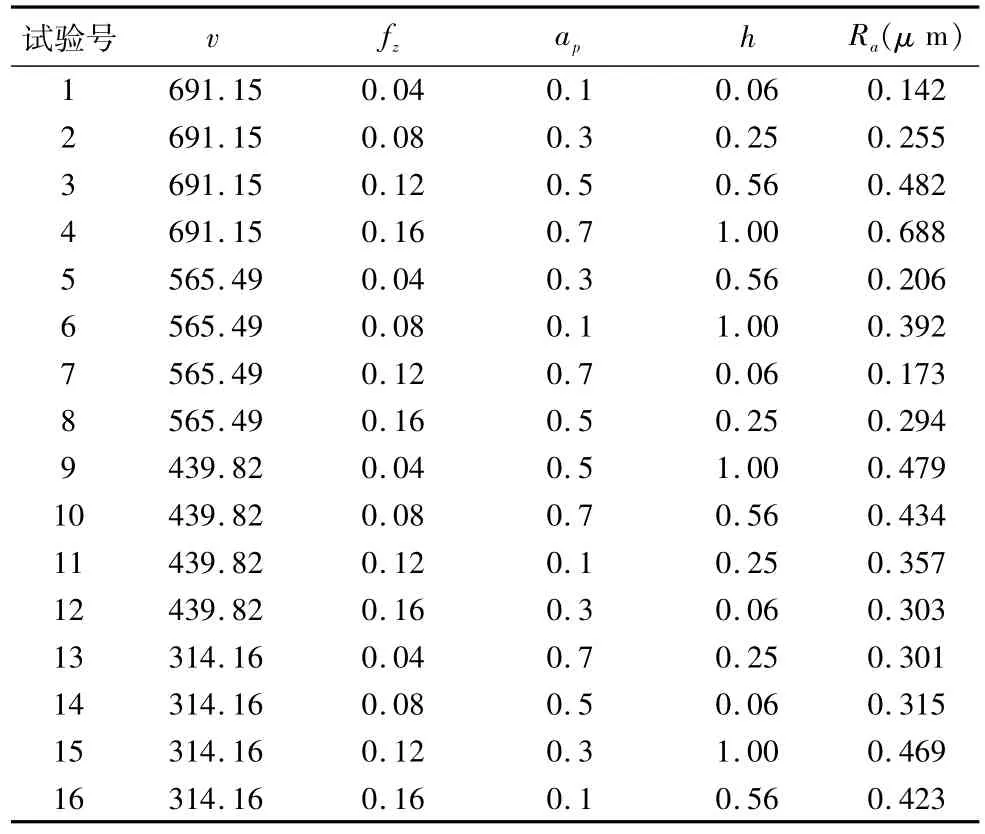
表2 表面粗糙度正交试验数据
表3列出的是粗糙度值Ra的极差分析内容。在极差分析表中,Ki(i=1,2,3,4)表示每一列中该因素对应的相同水平号试验结果的和。R是极差,其表达式为:
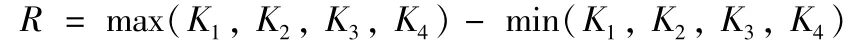
由表3中的结果可知,每一列极差值是不同的,意味着不同的因素水平变化对试验数据的影响不同。某一因素的极差R越大,表示该因素水平的变化对试验指标的数值波动影响越大。于是,可以得出极差值最大的那一列就是对表面粗糙度影响最显著的因素。从表中可以明显得知加工残留高度对表面粗糙度的影响最大,其次分别是每齿进给量、刀具线速度和轴向切深。

表3 表面粗糙度极差分析表
3 表面粗糙度数学模型构建
传统铣削表面粗糙度经验公式使用指数函数进行表达,而本文是在考虑加工残留高度对铣削表面质量影响的基础上开展的相关切削试验,因此可建立如式(1)的指数形式的预测模型,该模型包含了四个参数。
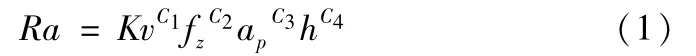
式中:K为切削条件综合系数;v为刀具切削线速度(m/min);fz为每齿进给量(mm/齿);ap为轴向切削深度,h为加工残留高度(μm),且,L为切削行距(mm),D为刀具直径。
式(1)为典型的非线性函数,须将其转化为线性函数,因此对其两边取常用对数,可以获得式(2)。

令y=Log Ra,C0=log(K),x1=log v,x2= log fz,x3=log ap,x4=log h,则指数方程可转化为线性方程(3)。

利用表2中的正交试验数据,对线性方程(3)进行多元线性回归,则可求解到方程中相应的系数:C0=0.4339,C1=-0.1484,C2=0.3078,C3= 0.1055,C4=0.2768,因此P20模具钢球刀铣削粗糙度的数学模型为式(4)。

为了判定预测模型拟合程度的好坏,有必要对表面粗糙数学模型进行显著性检验。采用F检验法,F=(SA/p)/(SE/(n-p-1))=7.58,(SA回归平方和,SE剩余平方和,n为试验组数,p为变量个数),F0.05(p,n-p-1)=F0.05(4,11)=3.36,因F>F0.05(p,n-p-1),所以该表面粗糙度的数学模型具有较高的显著性,能较好预测实际切削情况。
4 参数优化模型及求解
4.1 目标函数
铣削加工中,针对同一表面粗糙度技术要求可以得到多种工艺参数组合,本文的主要目标是选择合适的铣削参数组合使加工效率最高。目标函数的确定是实现参数优化的关键,这里用单位时间内球刀铣削面积的多少S来表示球刀精加工的效率,即如式(5)所示。

式(5)中S为球刀的加工效率(mm2/min),fz为每齿进给量(mm/齿),D为球刀直径(mm),L为切削行距(mm)。
在实际数控切削中,都希望产品在满足表面质量的前提下球刀的加工效率S能达到最大值,这样就可以提高企业的生产效益。寻找合适的数控切削参数,使得S达到最大值就成为了研究的内容,球刀精加工效率S最大值其形式可以表示为式(6):

4.2 约束条件
为了达到一定的表面质量,表面粗糙度Ra应小于等于某个常数;由于机床和刀具性能的限制,刀具的切削速度v应有一个范围;每齿进给量fz由于刀具性能的影响显然也是有范围的。结合P20模具钢切削试验的实际情况和零件质量的具体要求,给出如下约束条件:
(1)铣刀直径:D=10
(2)表面粗糙度:Ra≤0.3
(3)线切削速度:v≤450
(4)每齿进给量:0.04≤fz≤0.16
(5)本文只考虑精加工情况下表面粗糙度,因此将轴向切深参数ap设定为0.1mm的常数。
4.3 优化模型求解
球刀精加工效率S最大值的求解在数学上实际上已成为了典型的多元约束优化的求解。多元约束优化问题的求解非常复杂,手工计算难以完成,因此必须借助一些专用的数学求解工具。MATLAB是当今世界上最优秀的数学应用软件之一,它提供了一系列的专门用于优化问题求解的工具箱,这将复杂的优化问题求解变得简单。为了能够利用MATLAB优化工具箱,必须将实际问题转为MATLAB的标准形式,转化后的标准形式如下:
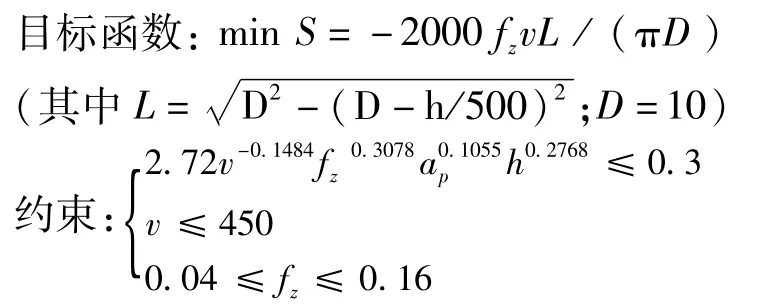
利用MATLAB优化工具箱中的fmincon函数,可以求解出上述多元约束优化问题,并获得如下优化参数:线速度 v为450m/min,每齿进给量 fz为0.16mm/齿,加工残留高度h为0.17μm,最大加工效率S为378mm2/min。因此在考虑刀具性能的情况下利用直径为φ10mm的球刀进行P20模具钢精加工,采用如下优化参数可以获得最大的加工效率:转速n为14330 r/min,进给速度F为4586mm/min,切削行距为0.08mm。
4.4 优化前后加工效率比较
实际加工中采用了试切法来确定数控加工工艺参数,而由于试切法的局限它只能保证产品的加工质量而无法同时保证加工效率达到最大化。通过大量试验,找到了一组工艺参数可以使产品表面质量达到要求(表面粗糙度Ra≤0.3),该组加工工艺参数如下:转速n为12000r/min,进给速度F为1200mm/min,切削行距为0.15mm。利用球刀精加工效率计算公式(6)可以获得该组工艺参数的加工效率 S为180 mm2/min,而利用优化的工艺参数其加工效率可达378 mm2/min,因此通过优化技术,在保证加工表面质量的前提下可将加工效率提高2倍多。
5 结论
(1)通过选定参数及切削试验建立了P20球刀铣削粗糙度预测模型,通过回归方程的显著性检验,证明了预测模型的可信度非常高。通过极差分析,可知影响P20球刀铣削粗糙度的因素依次是加工残留高度、每齿进给量、刀具线速度和轴向切深。
(2)加工残留高度是球刀铣削粗糙度最重要的影响因素,为了获得较好的表面加工质量,应设置较小切削行距以控制合适的加工残留高度。刀具切削速度和轴向切深对表面粗糙度影响比较小,为了提高加工效率在刀具和机床性能允许的情况下可以设置较大的刀具切削速度和轴向切深。
(3)以加工效率为目标函数和以粗糙度预测模型为约束条件,基于优化技术和MATLAB优化工具箱,获得了表面粗糙度Ra≤0.3时的优化切削工艺参数。通过对优化前后的工艺参数比较,可以得到如下结论:在保证加工表面质量的前提下,优化工艺参数可以大幅提高球刀加工效率。
[1]张德丰.MATLAB实用数值分析[M].北京:清华大学出版社,2012.
[2]马莉.MATLAB数学实验与建模[M].北京:清华大学出版社,2010.
[3]张伯霖.高速切削技术及应用[M].北京:机械工业出版社,2002.
[4]胡知音,孟广耀,夏海涛.基于正交试验法的GH4169高速铣削表面粗糙度研究[J].制造技术与机床,2011(1):44-46.
[5]柴桦,黄云,王亚杰,等.镁合金表面粗糙度预测模型优化的研究[J].机械科学与技术,2012,31(6):968-971.[6]田欣利,佘安英.基于回归分析方法的铣削表面粗糙度预测模型的建立[J].制造技术与机床,2008(11):101-104.
[7]陈青艳,胡成龙,杜军.加工精度和金属切除率的精车切削优化[J].组合机床与自动化加工技术,2013(3):111-114.
[8]龙超.高速铣削P20模具钢表面粗糙度与铣削参数的研究[D].秦皇岛:燕山大学,2011.
[9]VIVANCOS J,LUISC J,COSTA L.Optimal machining parameters selection in high speed milling of hardened steels for injection moulds.Journal of Materials Processing Technology,2004(155-156):1505-1502.
[10]林峰.不锈钢切削参数优化[J].暨南大学学报(自然科学版),2007,28(3):276-278.
[11]郭秀华,陈详林.基于高速铣削铝合金6061表面粗糙度试验研究[J].机床与液压,2011,39(6):38-39.
[12]张德强,宿永起,程杰,等.切削参数对Q235表面粗糙度影响试验研究[J].机械设计与制造,2013(10):142-144.
[13]朱小平,王涛.基于多目标粒子群算法的切削用量多决策优化研究[J].组合机床与自动化加工技术,2010(3):27-30.
Modeling of Surface Roughness with Ball-end Cutters Milling Based on Scallop Height and Optimum of Cutting Parameters
XIAO Jun-min1,2
(Department of Mechanical and Electrical Engineering,Zhongshan Polytechnic,Zhongshan Guangdong 528404,China)
The affecting factors on surface roughness are studied based on NC milling tests with ball-end cutters for P20 mould steel.Based on the analysis of the test data conclusions are as follows:scallop height is the most important influencing factors of surface roughness for ball-end cutters milling.Based on the experimental data,the mathematical model of surface roughness with ball-end cutters milling for P20 mould steel is derived and solved by using of regression analysis method of least square.Aiming at the actual milling problem the cutting parameters are optimized by using of optimum tool-box of MATLAB software and optimal design method.The optimized cutting parameters can greatly improve the machining efficiency ensuring quality of the machined surface,it provides the important theory evidence and case reference for NC machining enterprises to reduce production costs.
high-speed milling;scallop height;NC machining;surface roughness
TH162;TG501
A
1001-2265(2015)01-0054-03 DOI:10.13462/j.cnki.mmtamt.2015.01.015
2014-04-16
广东省高等学校优秀青年教师培养计划资助项目(Yq2013195)
肖军民(1978—),男,江西峡江人,中山职业技术学院副教授,硕士,研究方向为先进制造技术,(E-mail)xiaojunmin517@163.com。
