基于压缩感知的双向阈值匹配追踪算法
2015-11-02黄宏伟谢正光蒋小燕蔡旭
黄宏伟,谢正光,蒋小燕,蔡旭
(南通大学电子信息学院,江苏南通226019)
基于压缩感知的双向阈值匹配追踪算法
黄宏伟,谢正光,蒋小燕,蔡旭
(南通大学电子信息学院,江苏南通226019)
最近提出的前向后向算法(Forward-backward Pursuit,FBP)因为重构精度较高受到人们更多关注。但是FBP算法没有考虑到当前迭代残差信号的变化,每次迭代选取的原子和删减原子的数目是固定的。鉴于此,提出了双向阈值匹配追踪算法(Ovonic Threshold Matching Pursuit,OTMP)。OTMP前向原子选择过程通过限制等距性质(RIP)和残差的条件选出部分新增加原子,在回溯过程中通过当前迭代的重构水平剔除可能错误的原子。实验表明,在一定条件下OTMP时间复杂度和正交匹配追踪算法(Orthogonal Matching Pursuit,OMP),子空间追踪算法(Subspace Pursuit,SP)相当,重构精度明显高于SP,FBP算法和其他几种贪婪算法。
压缩感知;贪婪算法;原子;回溯;子空间追踪算法;前向后向算法
【本文献信息】黄宏伟,谢正光,蒋小燕,等.基于压缩感知的双向阈值匹配追踪算法[J].电视技术,2015,39(10).
传统信息论中,奈奎斯特(Nyqusit)指出信号的采样速率必须大于等于信号最高频率的两倍才能从采样信号完全恢复出原始信号。而这个过程伴随着大量的冗余信息,浪费了不必要的硬件采集资源。
一种新的信号采集技术压缩感知(Compressed Sensing,CS)[1],因其高效的采集效率逐渐吸引人们的学习研究兴趣。它采用边采集边压缩的模式,在数据采集过程中就进行适当的压缩,这样能保证信号采样速度低于奈奎斯特采样速率,减少不必要的资源浪费[2-3]。CS理论主要内容是可压缩信号的少量线性投影包含了原始信号的主要信息,利用全局的线性测量可以精确重构出原信号[4]。假设一个长度为N的一维信号x∈RN,x中非零原始个数K≪N,或者在某个正交基ψ稀疏表示θ中有K个非零值,x=ψθ,CS理论框架下,信号测量过程表示为

式中:y是长度为M的观测信号;Φ=[Φ1,Φ2,…,ΦN]是测量矩阵,大小为M×N;x为K阶稀疏信号,长度为N,K<M<N。这个过程相当于把原始信号x投影到[Φ1,Φ2,…,ΦN]张成的空间上,信号从N维降到M维。压缩感知中重构算法是核心内容,是从测量矩阵Φ和观测信号y中恢复原始稀疏信号x。从测量矩阵和原始信号维数可以看出式(1)是欠定的,求解原始信号是一个病态问题。但是当原信号只有有限的非零元素时,可以精确求解x。Candes和Donoho指出当测量矩阵和稀疏信号满足一定条件可以求助于非线性凸优化方法,如基追踪(BP)进行求解。但是BP算法复杂度太高,极大影响了它的实际应用。贪婪算法因为结构简单,运行速度快吸引了人们的广泛关注。带有回溯思想的贪婪算法因其重构精度较高备受人们关注。根据前向原子选择和后向原子删除步长,算法可分为步长为恒定值的算法和步长可变的算法。步长恒定算法包括子空间追踪算法(Subspace Pursuit,SP)[5]前向步长每次跟新K,后向删除步长也为K;压缩采样匹配追踪算法(Comprssive Sampling Matching Pursuit,CoSaMP)[6]前向步长每次跟新2K,后向删减步长也为2K;FBP[7]算法每次迭代前向跟新步长为α,后向删减步长为β,其中α>β。步长变化算法包括:自适应稀疏度匹配追踪算法(Adaptive Sparse Matching Pursuit,ASMP)[8]前向步长根据信号相关阈值得出,不是一个固定值,后向删减部分和SP类似,保留当前估计信号幅值最大K的索引;自适应阈值回溯正交匹配追踪算法(Adaptive Threshold Backtracking OMP,ATBOMP)[9]前向步长和信号相关,通过相关性求出阈值,再根据阈值选出原子,步长是变化的,后向删减步长是通过正则化完成的,步长也是变化的。
文献[7]提出了前向后向追踪算法(Forward-backward Pursuit),首先算法不需要稀疏度条件,其次算法重构精度相对较高。大部分情况,原信号的稀疏度是未知的,因此FBP相对于OMP[10-11],SP算法占有很大优势,其次FBP算法带有回溯机制,可以在迭代过程中自主纠错。虽然FBP算法相对于经典的几种算法占据优势,但是也存在缺点,首先是算法的时间复杂度,因为前向和后向步长是固定值,没有考虑迭代过程中信号的变化,所以执行效率比较低;其次算法重构精度还是有待进一步提高。本文提出双向阈值匹配追踪算法(OTMP)。实验证明,OTMP在一定条件下,重构精度和时间复杂度均优于FBP。
1 FBP
首先简单说明本文涉及的符号。supp(x)表示向量x中非零元素的位置。K表示稀疏度。ΦT表示Φ的转置,T0定义为初始的支撑集,r0表示初始的残差,Tl表示第l次迭代得出的支撑集,||Tl表示Tl中元素个数。rl表示第l次迭代得出的信号残差,xTl表示x对应Tl位置上的元素集合。δK+1为K+1阶RIP常数,hl=ΦTrl-1表示第l次迭代的代理信号,hl(i)=<Φei,rl-1>表示代理信号中的元素,其中<·>表示内积运算,ei为单位矩阵的第i列。
算法1:FBP算法
输入:测量矩阵Φ,测量向量y。
设置:前向步长α,后向步长β,最大迭代次数lmax,算法终止阈值ε。
初始化:T0=∅,r0=y,k=0。
迭代:k=k+1。
前向更新

后向更新

投影

如果||rl||2≤ε||y||2或|Tl|≥lmax,迭代终止,否则继续迭代。
迭代终止后令x͂=0,x͂Tl=w,输出x͂。
文献[7]指出,当稀疏信号中的非零元素不为一个常数值随机信号(Constant Amplitude Random Signal,CARS)时,FBP重构性能高于OMP,SP,BP算法。同时当稀疏信号非零值取值范围增大时,FBP重构精度相对BP将更加精确。文献还提出如果减小α,β的取值,将会减小算法运行时间,但是通过实验结果可以发现时间复杂度降低是用信号重构精度降低为代价换来的。
2 OTMP算法
FBP每次迭代选取原子的数量为一个固定的常数,而不考虑信号的性质(准确为残差信号性质),其次在后向更新过程,FBP每次迭代删减支撑集数量也为一个固定的常数,同样没有考虑迭代过程中信号的变化。FBP执行效率比较低;其次算法重构精度还是有待进一步提高。鉴于FBP缺点,本文提出OTMP。
2.1OTMP算法介绍
OTMP在支撑集选取过程充分考虑残差信号的特点选取满足条件的原子,随后把选出的原子加入到候选支撑集中。在原子筛选过程,首先计算测量向量y在候选支撑集张成空间上的正交投影,然后在所有投影系数中找出当前迭代新添加支撑集上的投影系数,并求和筛选阈值σ2,最后根据所求阈值剔除可能错误的原子。
算法2 OTMP算法
输入:测量矩阵Φ,测量向量y,最大迭代次数lmax,迭代终止阈值ε;
初始化:迭代次数l=0,残差r0=y,估计支撑集,原信号非零值估计
循环:令l=l+1,执行步骤1)~2)直到满足迭代终止条件。
1)支撑集选取:计算相关值Vl=(Φ')Trl-1,选定索引集w,使,计算支撑集选取阈值,选择Tf使令,更新Tf=w(1:λl),合并支撑集,最后利用最小二乘法求
2.2OTMP算法分析
2.2.1预备知识
1)限制等距性质(RIP)[5]定义
如果矩阵Φ∈RM×N满足参数为(K,δ)的有限等距性质,K≤M,0≤δ<1。对于任意的K阶稀疏信号有:
2)引理
引理1[12]对于任意的两个正整数m≤n,有δm≤δn。
引理2[13]设那么
2.2.2σ1阈值
当l=1,贪婪算法大部分是通过代理信号的幅值选择原子。假设矩阵Φ∈RM×N满足参数为(K,δ)的有限等距性质,根据引理2有:

同理当l>1
∀i∉supp(x),

2.3.3支撑集筛选原理
由于测量矩阵不是完全正交,因此通过支撑集选取过程得出候选原子并非一定完全正确。OTMP通过当前迭代产生的进行原子筛选,从物理意义上可理解为当前迭代选出原子的重构水平。如果本次迭代之前产生的正交投影系数幅值小于当前迭代重构水平(筛选阈值σ2需要当前重构水平乘以μ),那么可以认为之前选择的原子是错误的。通过这个原理可以剔除部分错误原子。随着迭代过程,原子不断被选入支撑集,当残差rl充分小或者迭代达最大次数lmax,算法终止,输出估计信号x̂。
3 实验
本文基于MATLAB仿真平台,对一维信号和二维信号都进行了相关实验。在一维信号部分,选择了三种不同类型的稀疏信号分别为高斯信号,“0-1”信号和均匀分布信号。二维信号则是标准的256×256的Lena测试图像。测量矩阵Φ的元素服从均值为0,方差为的高斯分布。
3.1一维信号仿真实验
测量次数M=128,信号长度N=256。稀疏度K取值应该满足K≤M/2。OMP和OTMP迭代停止阈值相同,均取ε=10-6,OTMP的最大迭代次数lmax=M,δ'=0.1(δ'是δK+1所求值放缩后的取值,这里不表示RIP常数),μ=0.18。BP算法重构是通过cvx工具箱实现的。FBP算法给前长步分别为α=30、20、2与之对应的后退步长β=29,19,1。停止阈值ε=10-6,最大迭代次数lmax=M/2。重构成功条件:,重建误差用平均归一化最小均方误差(Average Normalized Mean-Squared-Error,ANMSE)来表示均方误差,其中500表示独立的500次实验。
图1表示不同稀疏度条件下,各种算法对高斯信号重构效果。图1的第2幅曲线表示重构百分比和稀疏度之间关系,它可以衡量算法的稳定性。稀疏度较小时,所有算法都能保证100%重构出原信号。随着稀疏度不断增大,部分算法开始出现重构失败情况,而出现失败的临界点对算法评价具有重要意义。从曲线不难看出OMP算法在K=30之前就出现失败情况(为了突出重点,截去原曲线的前面部分内容),当K≥35,BP开始出现重构失败情况;当K≥43,FBP(2,1)开始出现重构失败;K≥45,FBP(20,19)和FBP(30,29)也出现失败情况。但是对于OTMP,只有当K≥56才出现重构失败情况,而且当K=61时其他算法重构概率几乎都降到0,OTMP却依然保持96%左右的水平。图1第3幅图表示重构的均方误差,它可以衡量算法重构的精确性,从图中可以明显看出OTMP重构的均方误差低于其他任何一种算法,而且在整个稀疏度区间都保持较低的值。最后分析图1的第1幅图,它表示重构时间和稀疏度之间的关系。OTMP算法在稀疏度1~51区间保持较低的运行时间,略高于OMP,SP,从K=51开始,随着稀疏度增加算法运行时间增长很快,当K=61,运行时间已经超过FBP(2,1)情况。但是从另一方面来看,如果只关心开始出现重构失败的临界点之前所有稀疏度对应的重构性能,OTMP时间复杂度相对于FBP还是较低的。
图2表示不同稀疏度条件下,各种算法对“0-1”信号重构效果。图2中间曲线可以看出,稀疏度K取26~28左右,FBP出现重构失败现象,SP在K≥29出现失败,而OTMP重构100%重构一直保持到K=36左右,这和BP算法十分相近。图2右边曲线表示重构的均方误差,OTMP重构误差仅次于BP算法,明显优于其他所有算法。最后在分析算法的时间复杂度,和高斯信号结果相似,在稀疏度相对较小时,OTMP保持较低的重构时间,与SP,OMP相当。但是当K=35时,随着稀疏继续增大,OTMP运行时间增长十分迅速,到K=40时,重构时间已经超过所有算法(不考虑BP时间)。同样,如果只关心开始出现重构失败的临界点之前所有稀疏度对应的重构性能,OTMP重构时间还是比较低的。最后是图3的均匀信号重构情况,性能分析与高斯信号相似,这里不再赘述。
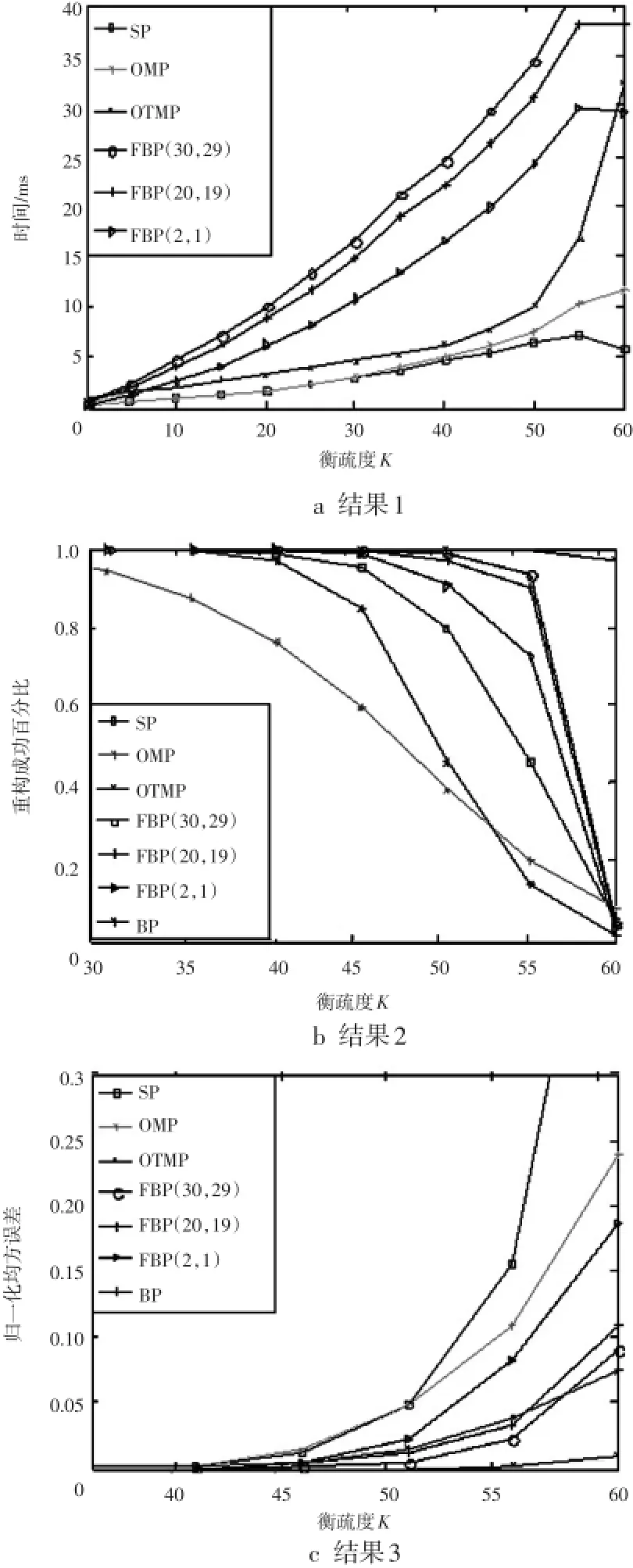
图1 高斯信号重构结果

图2 “0-1”信号重构结果

图3 均匀信号重构结果
3.2二维图像信号仿真实验
为了衡量算法对图像信号重构性能,选择标准的256×256Lena测试图像。首先对图像信号进行小波变换,选择sym6小波基。保留小波变换后系数矩阵每列最大的q个小波系数,其余置零。计算:重构的精度上OTMP的PSNR为34.4 dB,在其他所有算法中最大,即重构最精确;重构时间上OTMP的TIME是3.1 s,在其他所有算法中最小,即重构最快。二维图像经过二维小波变换,得出一系列小波系数,然后取出每列中最大的q个系数,其余置零,这样一方面可以节约重构时间,另一方面可以降低小的小波系数对重构的影响,即可提高重构精度,经过这样处理,图像信号每列的小波系数变为严格,且稀疏度已知的一维信号。对于一维信号,仿真结果显示,信号稀疏度在相对较小时,OTMP重构的均方误差很小,同时重构时间很短,接近SP,OMP。在二维实验中q取45对应OTMP算法参数设置与一维信号相同。
图4和表1反映了q=45条件下,几种算法重构结果。稀疏较小,所以不仅能精确重构而且重构所需时间很短。因此OTMP算法在二维图像信号重构上性能相比其他算法更加优越。

图4Lena图像重构,其中q=45

表1q=45时,算法重构的峰值信噪比和重构时间
4结论
本文提出一种新的贪婪重构算法双阈值匹配追踪算法OTMP。OTMP算法迭代有两个过程,支撑集选取和支撑集筛选。在支撑集选取过程,通过RIP性质和信号残差求出原子选择阈值,然后根据阈值选择满足条件的所有原子;在支撑集筛选步骤,通过当前迭代产生的或者进行原子筛选。实验仿真结果表明,对于高斯信号,OTMP重构精度高于包括FBP算法在内的所有算法,在整个稀疏度取值区间,重构误差保持在一个非常低的水平;对于“0-1”信号,OTMP算法重构效果明显高于其他贪婪算法,接近BP;对于二维图像信号,OTMP不仅重构精度高于其他所有算法,而且重构时间最短。
[1]CANDES E J,WAKIN M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[2]石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
[3]戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011,34(3)425-434.
[4]方红,杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421.
[5]DAI W,MILENKOVIC O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Trans.Information Theory,2009,55(5):2230-2249.
[6]NEEDELL D,TROPP J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321.
[7]KARAHANOGLU N B,ERDOGAN H.Compressed sensing signal recovery via forward-backward pursuit[J].Digital Signal Processing,2013,23(5):1539-1548.
[8]WU H,WANG S.Adaptive sparsity matching pursuit algorithm for sparse reconstruction[J].IEEE Signal Processing Letters,2012,19(8):471-474.
[9]HAO Z,GONG Z.Adaptive threshold backtracking matching pursuit for compressive sensing[C]//Proc.Radar Conference 2013.[S. l.]:IET Press,2013:1-4.
[10]TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Trans.Information Theory,2007,53(12):4655-4666.
[11]WU R,HUANG W,CHEN D R.The exact support recovery of sparse signals with noise via orthogonal matching pursuit[J]. IEEE Signal Processing Letters,2013,20(4):403-406.
[12]NEEDELL D,VERSHYNIN R.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J].Foundations of computational mathematics,2009,9(3):317-334.
[13]CANDES E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique,2008,346(9):589-592.
[14]MO Q,SHEN Y.A remark on the restricted isometry property in orthogonal matching pursuit[J].IEEE Trans.Information Theory,2012,58(6):3654-3656.
黄宏伟(1989—),硕士生,主要研究方向为数字信号处理;
谢正光(1967—),博士,教授,主要研究方向为智能信息处理、图像视频信号处理与传输;
蒋小燕(1989—),女,硕士生,主要研究方向为信号处理。
蔡旭(1990—),硕士生,主要研究方向为信号处理。
Ovonic Threshold Matching Pursuit for Sparse Signal Reconstruction Based on Compressed Sensing
HUANG Hongwei,XIE Zhengguang,JIANG Xiaoyan,CAI Xu
(School of Electronics and Information,Nantong University,Jiangsu Nantong 226019,China)
Due to high accuracy in signal reconstruction,Forward-backward Pursuit algorithm(FBP)has received more attention.However,the change of residual signal is not considered,and the number of atoms selected in each iteration is a constant.As a result,Ovonic Threshold Matching Pursuit(OTMP)is put up.On the one hand,OTMP tries to pick out part new atoms by Restricted Isometry Property and residual condition in the forward atom selection process.On the other hand,based on reconstruction level of current iteration,some atoms which are probably wrong are deleted.The experimental result shows that under certain condition,time complexity of OTMP is comparable with OMP,SP.Meanwhile,the reconstruction accuracy of OTMP surpasses SP,FBP and other greedy algorithms obviously.
compressed sensing;greedy algorithm;atom;backtracking;SP;FBP
TN911.73
A
10.16280/j.videoe.2015.10.002
时雯
2014-08-08
国家自然科学基金面上项目(61171077)
