多岩性信息融合在砂泥岩孔隙度预测中的应用

张宏兵,滕新保,曹呈浩,梁立锋,2,余　攀

(1.河海大学 地球科学与工程学院,南京 210098;2.中海油能源发展工程技术物探技术研究所, 广东 湛江 524000;3大庆油田海拉尔石油勘探开发指挥部,黑龙江 大庆 163453)



多岩性信息融合在砂泥岩孔隙度预测中的应用

张宏兵1,滕新保1,曹呈浩1,梁立锋1,2,余攀3

(1.河海大学 地球科学与工程学院,南京 210098;2.中海油能源发展工程技术物探技术研究所, 广东 湛江 524000;3大庆油田海拉尔石油勘探开发指挥部,黑龙江 大庆 163453)

储层孔隙度是表征储油物性、建立各类地质模型的重要参数。支持向量回归机(SVR)凭借良好的非线性回归能力,在孔隙度预测中开始广泛应用。由于不同岩性的储层孔隙类型不同,孔隙度结构也存在较大差异,导致该方法的实际应用效果仍不理想。针对上述问题,在孔隙度预测模型中考虑了岩性信息,将样本岩性转化为一种与岩性变化相关性好的属性值,以此构造一种新的预测模型。使用网格粗选和网格精选相结合的方法,优选模型参数。网格粗选确定最优解的近似范围,网格精选可以在局部区间搜索到最优解。结果表明:利用优选参数建立的预测模型,在实际资料预测结果中,加入岩性信息可以提高储层孔隙度的预测精度,该方法可行。

孔隙度;支持向量回归机;岩性信息融合

0　引　言

储层孔隙度是衡量油气储层岩石中所含孔隙体积多少的参数,是表征储油物性、建立各类地质模型的最重要参数[1]。它不仅能反映岩石储存流体的能力,同时也是评价储油层和计算储量的一个重要指标[2]。因此,在石油勘探中,对储层孔隙度的预测十分重要。

测井资料是确定储层孔隙度的理想资料,常用的测井方法有纵横波速度、中子测井、自然伽马测井等[3]。近年来,方中于等[4-7]提出了用于储层参数预测的SVR方法。但由于不同岩性类别,孔隙的结构也不完全相同,仅仅使用测井数据建立预测模型,预测精度仍不能满足实际要求。

影响孔隙度的因素主要有颗粒排列方式(主要反映压实程度)、大小的差异(分选程度)、黏土含量、颗粒形状、胶结程度及类型等[8]。在众多因素中,岩性对孔隙度影响较大,研究发现,储层岩石类型不同,其孔隙类型往往不同,孔隙结构也存在较大差异[9]。这使得它们具有不同的孔隙度,由此可知,岩性决定了孔隙度的变化范围。以往在孔隙度预测中,没有考虑储层岩性的信息,基于上述分析,笔者在孔隙度预测过程中,着重考虑储层岩性变化的信息。通过加入与岩性变化具有很好的相关性的属性,建立新的储层孔隙度预测模型,以此探索对上述问题的解决方法,并以某油田三个测井数据展开实例研究。

1　支持向量回归机

支持向量机 (Support vector machine,SVM)是针对经典的二分类问题提出的,但是SVM也可以应用到回归领域,支持向量回归机(Support vector regression,SVR)即是支持向量机在回归估计领域的应用。其特点是:SVR的样本点没有类别之分,所寻求的最优超平面也不是使两类样本点之间的分类间隔最大,而是使所有样本点到最优超平面的距离之和最小。此时,算法的目标就是使两条边界线之间的距离尽可能的大,这样间隔内可以容纳更多的点,这时,求最优回归超平面同样等价于求两条边界线的最大间隔。

1.1原理

作为训练样本集T={((x1,y1),(x2,y2),…,(xl,yl)}(Rn×y)l}),其中i=1,2,…,l,l为样本数量,xi∈Rn作为输入向量,yi∈R为输出值。若数据不能在样本空间中使用线性函数回归,可以使用映射函数Φ(·)对样本进行非线性变换,将样本映射到可以使用线性回归的高维特征空间。

非线性回归函数可表示为

f(x)=〈w,Φ(x)〉+b，

(1)

其中,Φ(x)是x映射到高维特征空间的映射函数；b为函数的截距,b∈R；w为函数的斜率，w∈Rn。根据下面的凸二次规划问题，可得到式(1)中的回归函数:

(2)

引入Lagrange函数,并将问题求解转化为其对偶形式,解得

(3)

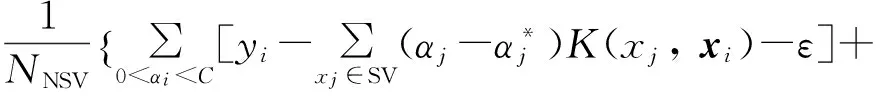
(4)

回归估计函数为

(5)

1.2核函数

SVM将样本高维特征空间的内积替换成了核函数,使得实际上的运算是在样本空间中进行的,避免了在特征空间直接计算,极大地减少了计算工作量。在SVM中不同的内积核函数将形成不同的算法,目前，常用的核函数主要有以下三种:

多项式型

K(xj，xi)=(p〈xj·xi〉+1)q；

(6)

RBF型

K(xj，xi)=exp{-γ‖ xj-xi‖2}；

(7)

S型

K(xj，xi)=tanh (υ〈xj·xi〉+c)。

(8)

由于S型核函数在孔隙度预测中很少用到,文中着重对比RBF型核函数与多项式型核函数的预测效果。

1.3参数优选方法

SVR模型中参数的选取决定了分类器的性能优劣[10-11]。常用的参数优选方法有网格搜索法、智能算法两类。网格搜索超参数存在搜索时间长、消耗和搜索范围无法确定的问题。智能算法(如遗传算法、粒子群算法等[12])具有快速收敛的优点,但算法操作复杂,且有容易陷入局部最优的缺点。

使用RBF核函数构建预测模型取决于径向核参数γ、不敏感参数ξ和惩罚参数C三个参数。其中ξ反映了噪声的大小,ξ的大小与输入噪声的方差线性相关[13];γ的大小与训练数据样本的分布特性有关;C的取值反映了SVR模型误差精度和复杂度之间的折衷,C取得大,模型存在过拟合的危险,影响模型的泛化能力,C取得小,则训练误差会变大。可以看出,三个参数在SVR模型中都有明确的意义,对于固定的样本,样本的分布特性(γ)和样本的噪声大小(ξ)是固定不变的。因此,在进行参数优选时,优选出的参数一定存在一些统计规律。

基于上述分析,笔者提出网格梯级搜索的方法。首先,使用网格粗选,根据粗选结果,找出统计规律,缩小参数的优选范围；然后，使用网格精选,局部范围搜索最优解。这样,既明确了搜索范围,又减少了搜索超参数带来的时间消耗。

2　描述岩性的特征属性

岩性是对岩心的一种定性描述,要想将岩性信息考虑到孔隙度预测模型中[14],必须要对岩性进行量化,这样形成的一种与样本点一一对应的数值,称为岩性的特征属性。量化方式有两种：一种就是直接将不同类的岩性标志为1、2、3等,如可以将砂岩类标志为1,粉砂岩标志为2,泥质粉砂岩标志为3,所得到的属性列称为硬岩性特征属性。但实际中岩性对孔隙度影响是渐变的,如泥质质量分数分别为25%和50%的泥质粉砂岩,二者虽然都命名为泥质粉砂岩,但二者的孔隙度随着泥质含量的不同,是不断变化的;随着泥质含量继续减小,泥质粉砂岩将过渡为粉砂岩,而硬岩性特征属性不能很好地表达岩性对孔隙度的这种过渡影响。另一种方法是通过对多个测井属性进行非线性变换、随进组合、主成分分析等,寻找出一种与岩性变化相关性较好的属性,所得到的属性列称为软岩性特征属性。

文中应用主成分分析法将多个测井属性合成三个特征属性,发现第一个特征属性与岩性的变化相关性很好,见图1。具体计算公式为

F1=0.347 1GR-0.319 8CNL-0.5Vp+0.486 1Vs,

(9)

其中,GR、CNL、Vp、Vs分别为自然伽马、中子、纵横波四种测井属性,属性数值已标准化。

从图1中可以看出,在软岩性特征属性上,砂岩与其余岩性类别整体上是分隔开的,而泥质粉砂岩和粉砂岩之间有一定的重合,这是由于二者孔隙度结构具有一定的相似性。

图1　软岩性属性和中子测井岩性交会图

Fig.1Lithology crossplot of soft rock properties andneutron logging

3　实例分析

实际资料处理中,使用国内某油田测区的三口井(井1、井2、井3)的测井数据,所使用的测井属性有自然伽马、中子、纵波速度等。使用图版法按照与孔隙度的相关性大小优选出纵波速度、中子、自然伽马、横波速度四个属性。三口井的储层岩性共有砂岩、粉砂岩、泥质粉砂岩三种,如表1所示。

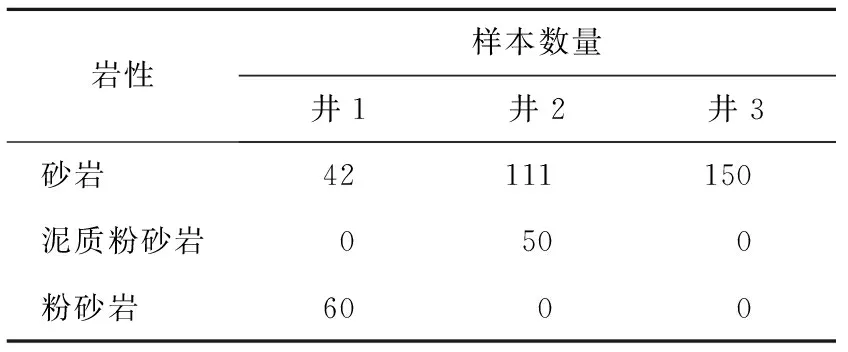
表1　岩性分布

井1、井2、井3的一半数据点作为训练样本,另一半作为预测样本。把作为输入属性的测井资料(自然伽马、中子测井、纵波速度、横波速度)、软硬岩性特征属性作归一化处理。将测井资料(方法一)、测井资料与硬岩性特征属性(方法二)、测井资料与软岩性特征属性(方法三)分别作为输入属性展开孔隙度预测。

3.1使用RBF核函数构建SVR预测模型

3.1.1参数优选

首先,使用网格搜索法对参数进行粗选,考察参数ξ固定在不同取值时,均方误差随参数γ和C变化。其中，γ和C分别在集合[2-8,2-7,…,27,28]和[10-1,100,…,105,106]中逐一取值,使用五重交叉验证方法对误差进行估计。将ξ固定在不同值时,使得均方误差达到最小值的参数γ和C记录在表2中。由于参数取值范围较大,分别以log10C和log2γ作为参数C和γ的刻度。表2中不敏感参数ξ与均方误差的对应关系如图2所示。

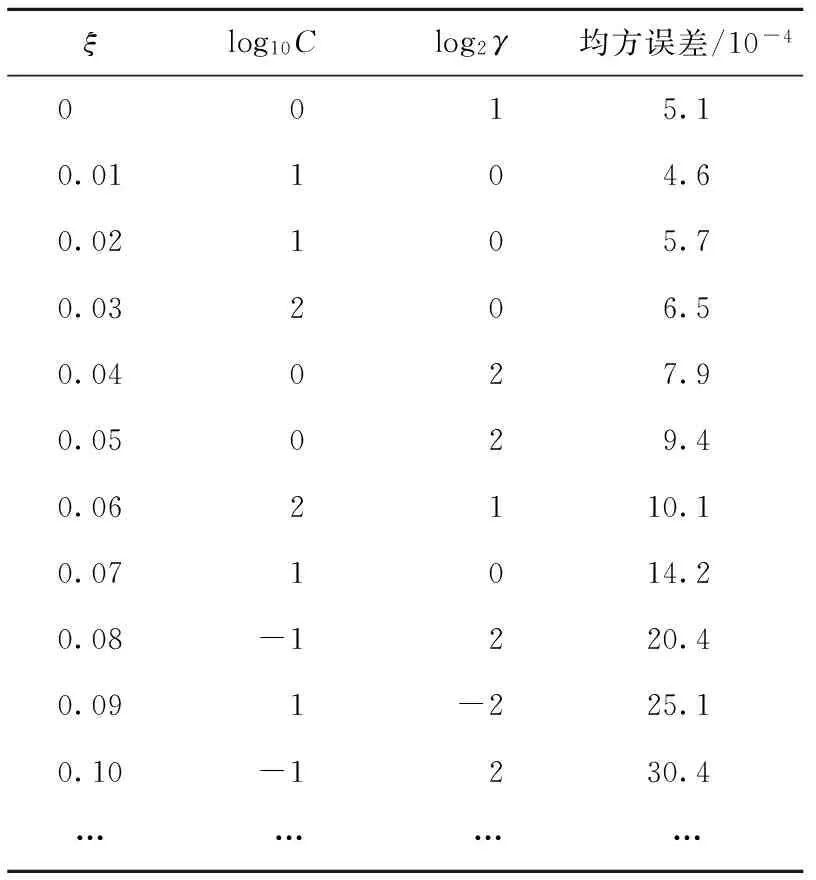
表2　优选的γ和C及均方误差与ξ的对应关系

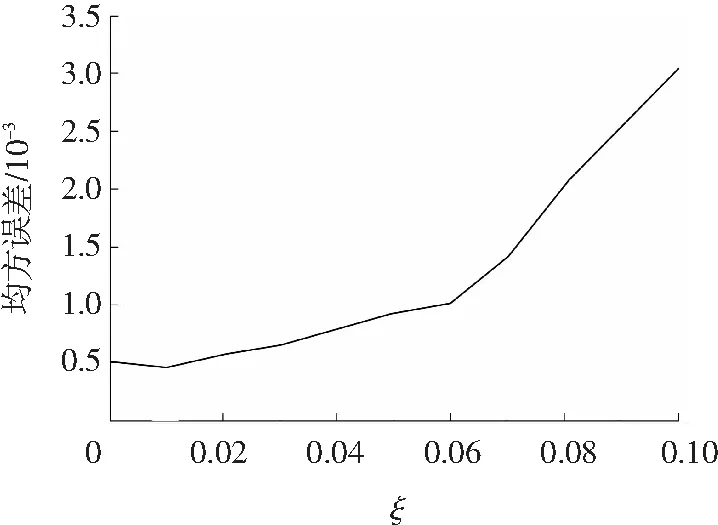
图2　均方误差随不敏感参数的变化关系

Fig.2MSE along with change of not sensitive parameters

由图2可以看出,当ξ不断增大时,均方误差先减小,后增大,在ξ=0.01处取到极小值,因此,ξ应当取0.01附近的值。从表2可以看出,随着ξ的变化,log2γ的变化总是在区间[-2,2]内,log10C的变化总是在区间[-1,2]内,故可将γ和C的优选范围分别缩小至[0,4]和[0,100]。

其次,使用网格搜索法对三参数进行精选。其中ξ、γ、C分别在区间[0,0.001,…,0.019,0.020]、[0.25,0.30,…,3.95,4.00]、[0,5,…,95,100]中取值,采用五重交叉验证方法进行误差估计。最终优选出模型参数:ξ=0.014,γ=0.55,C=20。

3.1.2预测结果分析

利用优选出来的参数建立预测模型,并对训练样本、预测样本分别进行估计,估计均方误差如表3所示。从表3可以看出,均方误差均小于7×10-4,说明支持向量机对孔隙度的预测效果是可观的。使用方法一,不管是对训练样本还是对预测样本,估计结果的均方误差都远大于使用方法二和方法三,说明在预测模型中加入岩性信息是有效的。虽然在对训练样本估计时,使用方法二和方法三的估计误差相当,但在对预测样本估计时,使用方法三的估计结果的均方误差远低于方法二。说明相对于硬岩性属性,在预测模型中加入软岩性属性,使预测模型具有更好的外推性能。

表3RBF核函数对孔隙度的预测效果

Table 3Porosity prediction effect of usingRBF kernel function

方法输入属性均方误差/10-4训练样本预测样本一测井参数5.86.5二测井参数+硬岩性属性3.65.9三测井参数+软岩性属性3.54.4

使用不同方法得到的孔隙度估计值随井深的变化关系如图3所示。从图3可以看出,使用方法三所得到的孔隙度估计值与真实孔隙度最接近。

3.2预测结果与使用多项式核函数的对比

运用多项式核函数构建SVR模型由四个参数决定,分别为多项式核参数p、q,惩罚参数C和不敏感参数ξ。前文中已经确定ξ的取值为0.014,使用网格搜索法对剩余三参数进行优选。优选出模型参数为C=3.52，p=0.1，q=5。

利用优选出的参数建立预测模型,并分别对训练样本、预测样本进行估计,预测效果见表4。对比表3和表4可以看出,运用多项式核函数建立模型的估计误差远高于运用RBF核函数,由此可得,在建立孔隙度预测模型的过程中,运用RBF核函数模型优于运用多项式核函数。

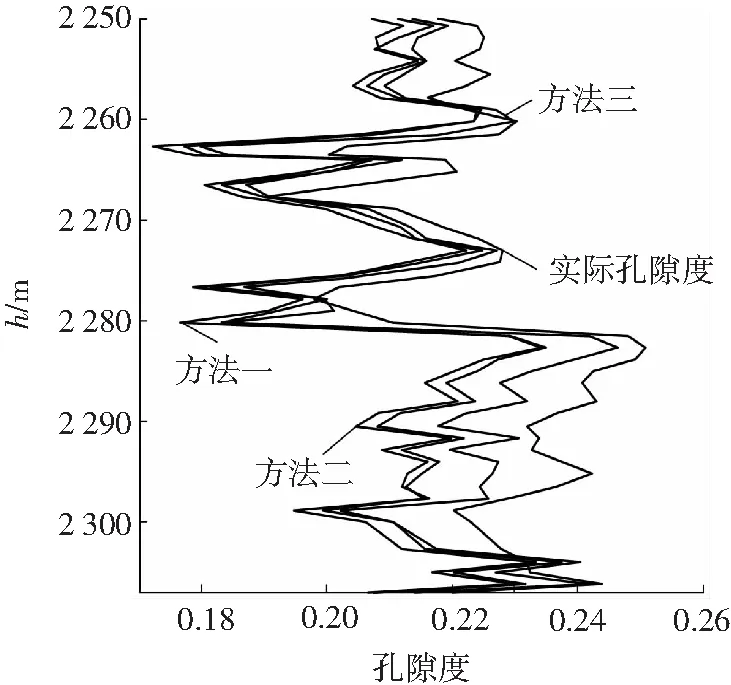
图3不同方法孔隙度估计值随深度的变化关系

Fig.3Porosity estimate changes with depthwhich use different methods

表4多项式核函数对孔隙度的预测效果

Table 4Porosity prediction effect of usingkernel polynomial function

方法输入属性均方误差/10-4训练样本预测样本一测井参数5165二测井参数+硬岩性属性4644三测井参数+软岩性属性4642

3.3预测结果与使用BP神经网络的对比

基于训练样本的训练得到的神经网络权值对样本进行预测,并与SVR预测结果作对比，预测效果见表5。

表5SVR和BP神经网络对孔隙度的预测效果对比

Table 5Collation map of porosity prediction effect ofusing SVR and BP neural network

输入属性均方误差/10-4SVR训练样本预测样本BP神经网络训练样本预测样本测井参数5.86.5333测井参数+硬岩性属性3.65.9434测井参数+软岩性属性3.54.4223

从表5可见,BP神经网络对训练样本的估计误差很低,但对于预测样本的估计精度明显高于运用SVR模型。这是由于神经网络存在过拟合的缺陷,因而在孔隙度预测过程中,SVR的预测效果优于BP神经网络。

4　结　论

(1)将岩性信息加入到输入属性中,建立新的预测模型,可以提高储层孔隙度的预测精度,方法可行。将硬岩性属性与软岩性属性分别加入输入属性中,对比得出,软岩性属性代替岩性的信息,能更好地代表岩性对孔隙的影响。

(2)文中提出的参数优选方法,即网格梯级搜索方法,在搜索效率和搜索精度上均有很大的提高,是一种合理的优选方法。

(3)在与SVR多项式核函数、神经网络建立的孔隙度模型对比中,使用SVR中的RBF核函数效果最好。

[1]陈欢庆,曹晨,梁淑贤， 等.储层孔隙结构研究进展[J].天然气地球科学,2013,24(2):227-237.

[2]黄思静,郎咸国,兰叶芳， 等.储层孔隙度-渗透率关系曲线中的截止孔隙度与储层质量[J].成都理工大学学报:自然科学版,2011,38(6):593-602.

[3]范铭涛,沈全意,吴辉,等.复杂岩性裂缝-孔隙型储层孔隙度计算方法研究[J].天然气工业,2005,25(5):29-30.

[4]方中于,万欢,李勇.W地区储层孔隙度地震预测技术及应用研究[J].矿物岩石,2012,32(3):110-115.

[5]朱永才,薛坤林.基于支持向量机的储层参数反演[J].广东石油化工学院学报,2012,22(1):44-46.

[6]张彦周， 王春香.支持向量机的测井数据预测储层渗透率方法[J].科技传播,2009,6(5):83-85.

[7]陈华,邓少贵,范宜仁.基于LS-SVM的测井物性参数的预测方法[J].计算机工程与应用,2007,43(23):208-210.

[8]史基安,王琪.影响碎屑岩天然气储层物性的主要控制因素[J].沉积学报,1995,13(2):128-139.

[9]赖锦,王贵文,王书南,等.碎屑岩储层成岩相研究现状及进展[J].地球科学进展,2013,28(1):39-50.

[10]廖士中,丁立中,贾磊.支持向量回归多参数的同时调节[J].南京大学学报：自然科学版,2009,45(5):585-592.

[11]李新虎.基于不同测井曲线参数集的支持向量机岩性识别对比[J].煤田地质与勘探,2007,35(3):72-76,80.

[12]熊伟丽,徐保国.基于PSO的SVR参数优化选择方法研究[J].系统仿真学报,2006,18(9):2442-2445.

[13]杨俊燕,张优云,朱永生.ε不敏感损失函数支持向量机分类性能研究[J].西安交通大学学报,2007,41(11):1315-1320.

[14]赵晓明,罗明高.储层岩性不同油藏孔隙度下限确定方法研究[J].大庆石油地质与开发,2008,27(1):90-92,96.

(编辑徐岩)

Multiple lithologic information fusion applied in sand mudstone porosity fitting

ZHANG Hongbing1,TENG Xinbao1,CAO Chenghao1,LIANG Lifeng1,2,YU Pan3

(1.School of Earth Science &Engineering,Hohai University,Nanjing 210098,China;2.Cnooc Energy Development Engineering Geophysical Prospecting Institute of Technology,Zhanjiang 524000,China;3.Hailar Petroleum Exploration &Development Headquarters of Daqing Oilfield,Daqing 163453,China)

This paper introduces a novel prediction model building on the deeper understanding that reservoir porosity is an important parameter by which to represent reservoir characteristics and thereby establish diverse geological models.This model is an alternative to SVR which has come into a wider use in the porosity prediction thanks to its ascendant nonlinear regression capability,but has been thwarted by the occurrence of the different types of reservoir pores with different lithology and more variations found in pore structure of the reservoirs.The model is developed by considering the lithology information and transforming the lithology information of the sample into a kind of attribution with a better relativity with lithology change by using the information confusion method.The model parameters are optimized by combining rough screening which determines the approximate scope of the optima with fine screening which provides the optima in a certain range.The results demonstrate that the model built with preferred parameters features a better precision in the practical application after provided with the lithology information.

porosity;SVR;lithology information fusion

2014-12-15

国家自然科学基金项目(41374116);中国海洋石油总公司科技项目(CNOOC-KJ 125 ZDXM 07 LTD NFGC 2014-04)

张宏兵(1968-),男,安徽省无为人,教授,博士,研究方向:地球物理正演及反演,E-mail:hbzhang@hhu.edu.cn。

10.3969/j.issn.2095-7262.2015.02.012

P618.13； TP183

2095-7262(2015)02-0172-05

A