深部巷道围岩瞬态温度-热应力的耦合作用

李铁增,王　丽,李玉梅

(1.山东省工程咨询院,济南 250013;2.山东科技大学 矿业与安全工程学院,山东 青岛,266590;3.兖矿集团邹城华建设计研究院,山东 邹城,273500)



深部巷道围岩瞬态温度-热应力的耦合作用

李铁增1,王丽2,李玉梅3

(1.山东省工程咨询院,济南 250013;2.山东科技大学 矿业与安全工程学院,山东 青岛,266590;3.兖矿集团邹城华建设计研究院,山东 邹城,273500)

为了研究深部巷道温度场与应力场的耦合作用,采用理论推导得到圆形巷道围岩瞬态热-弹性耦合解析解,分析了巷道围岩温度场和热应力的分布规律,并通过数值模拟和现场观测研究了热应力对巷道围岩稳定性的影响。研究表明:围岩温度分布呈非线性变化,表层温度梯度大,围岩深处温度梯度小;随通风时间延长,围岩温度逐渐降低,冷却圈不断增大,温度梯度逐渐减小,温度分布曲线趋于平缓;通风能够改变围岩应力状态,切向热应力在围岩表层表现为较大的拉应力,而在深处表现为较小的压应力;径向热应力为拉应力,热应力加剧了巷道围岩顶底板塑性区扩展的深度。

深部巷道;温度场;热应力场;巷道通风

0　引　言

随着矿井开采深度的增加,地温会不断升高。巷道围岩温度变化导致围岩产生相应变形,围岩内各点温度变化不同,在外约束和自身约束的作用下,温度变形不能自由发生,因此在巷道围岩内产生热应力,温度场和应力场耦合作用下巷道围岩破碎区半径、表面位移均有较大增加,巷道破坏加剧[1]。对于岩体温度场-应力场耦合作用,国内近几年做了大量研究。刘亚晨等[2]研究了岩体裂隙结构面温度-应力-水力耦合本构关系。陈剑文等[3]建立了盐岩在温度与应力耦合作用下的损伤本构方程并进行了实验验证。左建平等[4]根据最小耗能原理推导了温度和压力耦合作用下岩石的屈服破坏准则。贺玉龙等[5]对岩体温度场与应力场的耦合作用强度进行了量化分析。韦四江[6]研究了稳态温度场对巷道围岩应力和变形的影响。众多研究主要考虑的是稳态温度场对巷道围岩稳定性的影响,而实际上,围岩内各点温度是空间和时间的函数,因此,围岩内热应力分布并不均匀且随时间不断变化。通风降温条件不同、围岩热物理性质和力学性质不同,则热应力对巷道围岩稳定性的影响不同。

笔者通过理论推导圆形巷道围岩瞬态热-弹性耦合解析解,以期获得巷道围岩温度场和热应力的分布规律及其随时间变化的规律。结合工程实例,通过数值模拟和现场观测,研究在地应力和温度荷载作用下围岩塑性区随时间扩展的规律,分析热应力对围岩稳定性的影响。

1　围岩瞬态温度-热应力耦合解析解

根据岩石温度场与应力场耦合强度量化的研究成果[5],热弹性耦合通常是单向的,温度场变化对应力和变形的影响较大,而固体变形对温度场的影响较小。因此,在计算温度场时可以不考虑岩体应力场,先计算巷道围岩温度场,然后将温度场计算结果作为已知条件,计算巷道围岩应力场。

1.1平面轴对称温度场的解析解

常年通风巷道[7-8],围岩冷却圈的范围有限,且沿巷道轴向围岩温度差很小,热流密度几乎为零。当不考虑地应力作用时,可将巷道围岩温度场简化为第一类边界条件下的平面轴对称温度场。

假设巷道围岩初始温度均匀分布,外边界温度不变,等于围岩的初始温度,内边界温度等于流体温度,而且流体温度恒定,不随时间变化。假设函数T=T(r,t)表示巷道岩体内各点的温度(其中T为时间和空间的函数,单位为℃,t为时间),巷道内风流温度为Tc，引入过余温度θ(r，t)=T(r，t)-Tc，根据传热学原理,在圆柱坐标系中,对于平面轴对称温度场,初始条件和边界条件为:

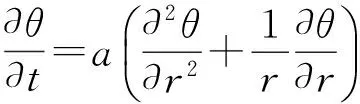
(1)

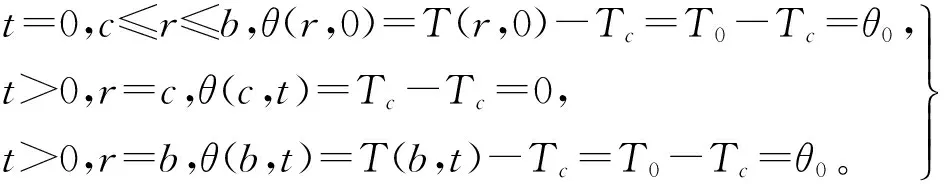
(2)

根据一般情况下的瞬态温度场理论解可得出巷道风流温度为Tc时围岩瞬态温度场的理论解:

(3)

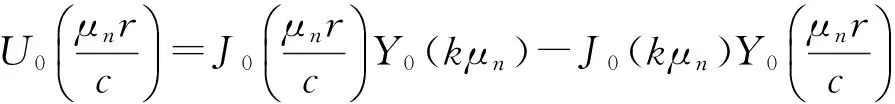
(4)

式中,J0、Y0为零阶的第一、二类贝塞尔函数;k=b/c,μn为特征方程(5)的根，

J0(μn)Y0(kμn)-Y0(μn)J0(kμn)=0。

(5)

1.2平面轴对称热应力的解析解

将巷道视为无限长圆筒,内半径为c,外半径为b,而且b远大于c。发生轴对称温度变化ΔT:

ΔT=T(r,t)-T0。

(6)

将巷道围岩瞬态温度场的理论解代入式(6)并整理得:

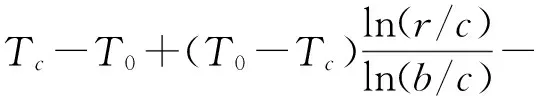
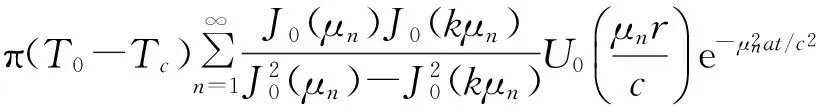
(7)

根据平面应变问题的热应力理论解,可得出巷道围岩的瞬态热应力场:

(8)

式中：E为弹性模量;α为热膨胀系数;μ为泊松比;σr为径向应力；σθ为切向应力；σz为轴向应力。

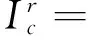
(9)

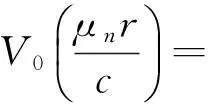
(10)

式中,J1、Y1为一阶的第一类、第二类贝塞尔函数。

1.3地应力作用下围岩应力场的解析解

假设深埋圆形巷道的半径为c,水平荷载对称于竖轴,竖向荷载对称于横轴。竖向荷载为p0,横向荷载为λp0,则巷道围岩的弹性应力为:

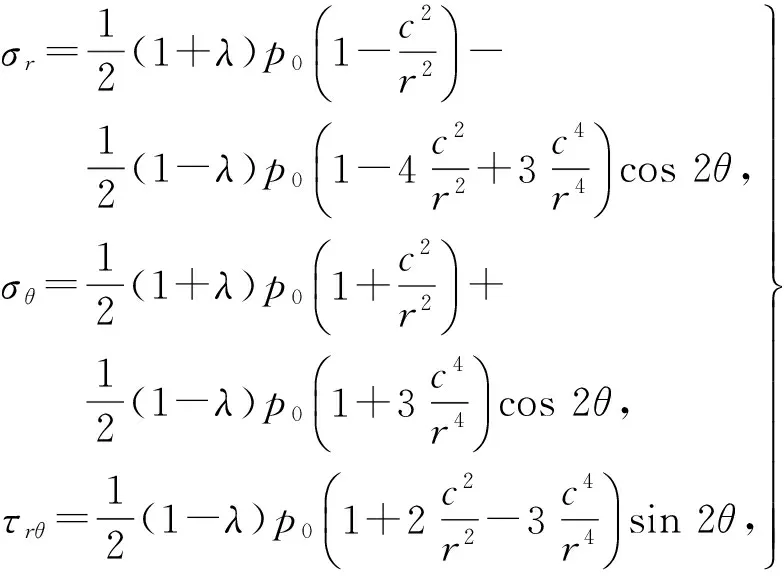
(11)

式中，2rθ为切应力。假设围岩处于弹性状态,将(8)式计算结果与(11)式计算结果进行叠加,即可得出温度荷载与地应力荷载共同作用下巷道围岩的弹性应力场。

2　圆形巷道围岩温度场及应力场规律分析

2.1围岩瞬态温度场及热应力理论分析

巷道通风初期围岩冷却圈半径较小,因此,将巷道看作厚壁圆筒。假设内半径为2 m,外半径为8 m,围岩初始温度为45 ℃,风流温度为15 ℃,岩石的热物理参数和力学参数如表1所示。由式(3)可计算出围岩瞬态温度场。J0、Y0由《数学物理方法》附表三查表确定。

图1围岩温度变化曲线

Table 1Thermal physical and mechanicalparameters of surrounding rock

G/GPaμα/℃-112.370.249.0×10-6ρ/kg·m-3λ/kJ·(m·h·℃)-1C/kJ·(kg·℃)-125208.280.88

图1为降温14、30、60 d后不同时刻围岩内温度分布曲线。随着降温时间的延长,围岩温度进一步降低,冷却圈不断增大。围岩内温度呈抛物线分布,围岩表层温度梯度较大,而围岩深处温度梯度较小,在足够远处温度梯度几乎为零。这与已有研究成果[9-11]得出的结论相同。

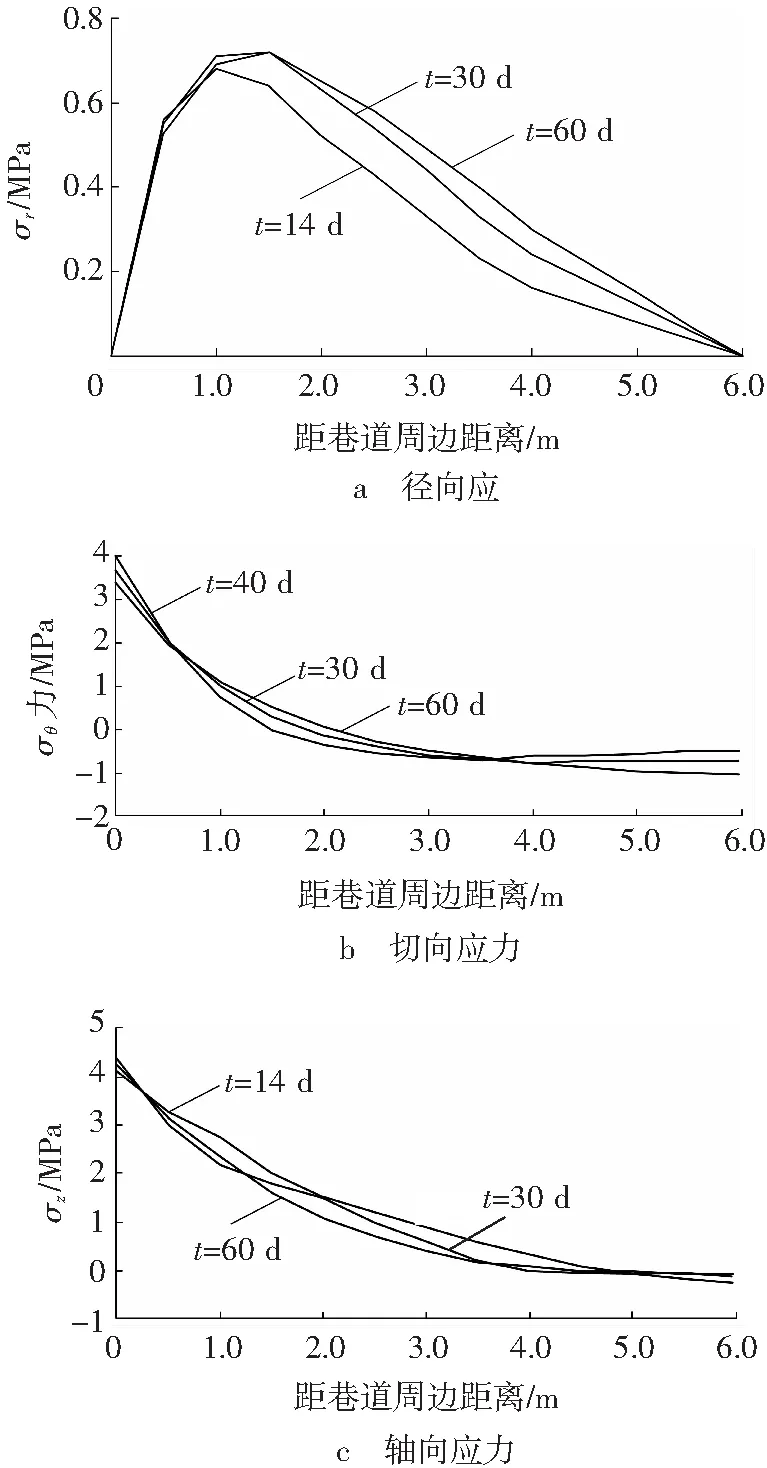
图2　围岩各应力分布

在轴对称温度变化的作用下,巷道通风后不同时刻巷道围岩热应力可直接由式(3)计算得出。图2给出了围岩内径向热应力、切向热应力和轴向热应力分布曲线。巷道通风降温过程中,径向热应力始终是拉应力,在巷道周边径向热应力为零,距巷道周边1.0～1.5 m处拉应力最大,然后逐渐减小;降温初期应力值较小,随后逐渐增大,但与切向热应力相比,量值较小。切向热应力在围岩表层一定范围内表现为拉应力,而在围岩深处表现为压应力,最大切向拉应力出现在巷道周边;降温初期,巷道周边切向拉应力较大,随后逐渐减小;最大切向压应力出现在距外缘一定距离处,降温初期其值较小,随后逐渐增加,最大切向压应力向围岩深处转移。轴向热应力在围岩表层一定范围内表现为拉应力,在围岩深处表现为压应力;其最大值出现在巷道周边位置;降温初期,轴向拉应力较大,随后逐渐减小。图2可以看出,随着通风降温时间的延长,拉应力区不断向外扩展,围岩深处的压应力不断增加。

2.2地应力与温度荷载耦合作用围岩应力分布规律

假定竖向荷载为20 MPa,侧压系数为0.32。由式(8)、(11)可计算出地应力与温度荷载共同作用下的围岩应力场。巷道通风降温14、30、60 d后不同时刻围岩径向应力、切向应力分布曲线如图3所示。

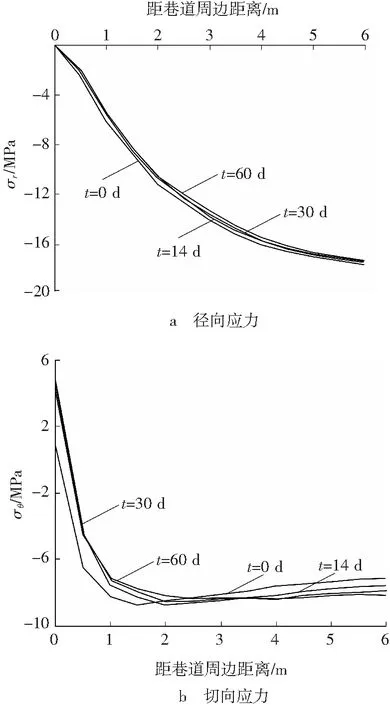
图3　径向与切向应力分布曲线

由于巷道通风降温,巷道顶底板周边出现较大切向拉应力,极易使巷道顶、底板表层围岩产生拉破坏,对巷道围岩稳定性极为不利。巷道围岩受力状态发生改变,在围岩表层一定范围内,切向应力由原来的拉应力变为压应力。随着通风降温时间的延长,围岩内压应力区逐渐扩展,围岩内径向压应力减小,巷道周边切向压应力减小,围岩深处切向压应力增加。同时,围岩内部主应力差增大,容易造成压剪破坏。

3　工程实例分析

3.1计算条件

新汶矿业集团孙村煤矿-1100西大巷埋深1 300 m,设计断面形状为马蹄形,底宽5 m、顶高4.5 m。采用锚网喷支护,锚杆采用φ20×2 000 mm的等强度螺纹钢锚杆,锚杆长度为2m,锚杆间排距为1 000×1 000 mm,喷射混凝土厚度150 mm,分两次完成。巷道位于粉砂岩中,岩层厚度为19.6 m,岩层倾角为29°,上部岩层为细砂岩,下部为砂岩。根据-1050东大巷地应力资料推测,最大水平主应力为45 MPa,基本上与巷道两帮垂直,垂直应力为32.5 MPa。实测巷道原岩温度为48 ℃,围岩热物理参数见表2,巷道围岩表面对流换热系数为86.8 kJ/(m2·h·℃)。巷道在冬季开掘,实测巷道风流温度如表3所示。围岩力学参数见表4。

表2围岩热物理参数

Table 2Thermal physical parameters of surrounding rock

围岩ρ/kg·m-3λ/kJ·(m·h·℃)-1C/kJ·(kg·℃)-1细砂岩268010.7650.88粉砂岩253010.8650.88砂岩273511.0270.86

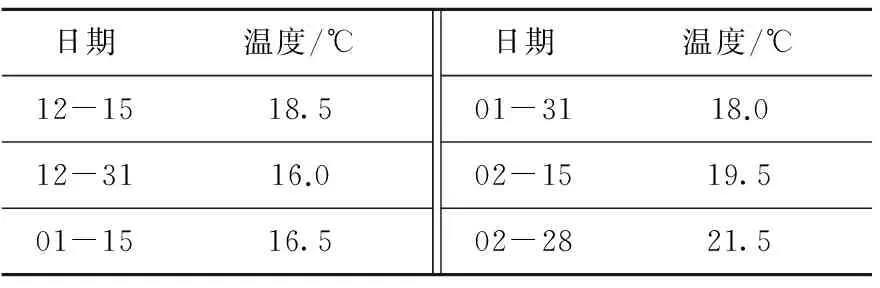
表3　巷道风流温度

3.2计算结果分析

针对以上条件,采用有限元软件ANASYS对巷道围岩进行了热—应力耦合分析。

表4围岩力学参数

Table 4Mechanical parameters of surrounding rock

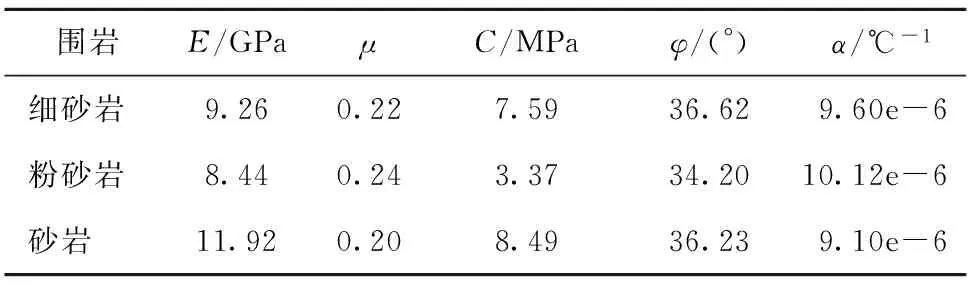
围岩E/GPaμC/MPaφ/(°)α/℃-1细砂岩9.260.227.5936.629.60e-6粉砂岩8.440.243.3734.2010.12e-6砂岩11.920.208.4936.239.10e-6

(1) 巷道围岩温度场结果对比分析

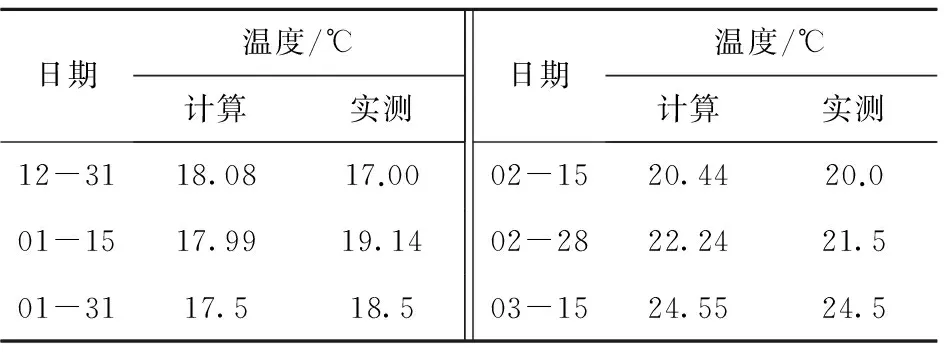
巷道通风后围岩温度场不断变化,不同时间巷道壁面温度的计算结果和实测结果如表5所示。与风流温度对比看出,巷道壁面温度与风流温度有一定差值,巷道壁面温度计算结果与实测结果比较接近。

表5巷道壁面温度计算结果与实测结果

Table 5Computed and measured result ofsurface temperature of roadway

日期温度/℃计算实测12-3118.0817.0001-1517.9919.1401-3117.518.5日期温度/℃计算实测02-1520.4420.002-2822.2421.503-1524.5524.5

(2) 围岩塑性区结果对比分析

巷道通风后,由于热应力作用巷道围岩塑性区逐渐扩展。开挖支护后,巷道顶底板及两帮均已出现塑性区。开挖一个月后底板塑性区深度为1.07 m,扩展了15%,顶板塑性区深度为0.53 m,扩展了17%,两帮塑性区扩展很少。开挖两个月和三个月后围岩塑性区几乎不再扩展。巷道塑性区扩展深度计算结果与实测结果对比如表6所示。

表6巷道塑性区扩展深度计算结果与实测结果

Table 6Computed and measured result of depth ofplastic zone of roadway

状态塑性区扩展深度/m底板顶板两帮模拟开挖支护后0.930.450.50模拟开挖2个月后1.070.530.51实测初次支护后1.100.600.70实测开挖2个月后1.300.700.80

巷道初次支护后围岩收敛变形仍然较大,在二次支护前用地质雷达对巷道围岩松动圈进行了测量,底板松动破坏深度为1.1 m,两帮松动破坏深度为0.7 m,顶板松动破坏深度为0.6 m。围岩松动破坏没有超过预估范围,二次支护按原设计方案进行。二次支护后巷道围岩收敛变形继续发展,掘进两个月后再次对巷道围岩松动圈进行测量,底板松动破坏深度为1.3 m,两帮松动破坏深度为0.8 m,顶板松动破坏深度为0.7 m。将实测结果与数值模拟结果对比发现,实测结果与数值模拟结果相差不大,热应力是引起巷道围岩塑性区扩展的原因之一,其对巷道稳定性的影响主要表现在顶底板破坏加剧。

4　结　论

将深部圆形巷道简化为第一类边界条件下的平面轴对称温度场和应力场,推导得到地应力和温度荷载共同作用下的热—弹性耦合解析解,并通过数值模拟与现场实测,研究了热应力对巷道围岩稳定性的影响。结论如下:

(1) 围岩温度分布呈非线性变化,表层温度变化大,温度梯度大,而深处温度变化小,温度梯度小,超过一定范围后温度几乎不再变化。随通风时间的延长,围岩温度进一步降低,冷却圈不断增大,温度梯度逐渐减小,温度分布曲线变得比较平缓。

(2) 由于巷道通风降温,围岩应力状态发生改变。切向热应力在围岩表层表现为较大的拉应力,而在围岩深处表现为较小的压应力;径向热应力在整个围岩内都是拉应力,巷道周边径向应力为零,距巷道周边较小深度处径向应力最大。

(3) 通过数值模拟和现场观测研究发现,巷道通风后,壁面温度和围岩塑性区计算结果与实测结果接近。由于热应力作用,顶底板塑性区扩展深度加剧。

[1]谭云亮,刘传孝,赵同彬.非线性岩石力学初论[M].北京：煤炭工业出版社,2008.

[2]刘亚晨,蔡永庆,刘泉声,等.岩体裂隙结构面的温度-应力-水力耦合本构关系[J].岩土工程学报,2001,23(2):196-200.

[3]陈剑文,杨春和,高小平,等.盐岩温度与应力耦合损伤研究[J].岩石力学与工程学报,2005,24(11):1986-1990.

[4]左建平,谢和平,周宏伟.温度压力耦合作用下的岩石屈服破坏研究[J].岩石力学与工程学报,2005,24(6):2917-2921.

[5]贺玉龙,杨立中,杨明.岩体温度场与应力场耦合作用的一种量化方法[J].西南交通大学学报,2002,37(1):10-13.[6]韦四江,勾攀峰,马建宏.深井巷道围岩应力场、应变场和温度场耦合作用研究[J].河南理工大学学报,2005,24(5):351-354.

[7]吴强,秦跃平,郭亮,等.巷道围岩非稳态温度场有限元分析[J].辽宁工程技术大学学报,2002,21(5):604-607.

[8]高建良,杨明.巷道围岩温度分布及调热圈半径的影响因素分析[J].中国安全科学学报,2005,12(2):73-76.

[9]张树光,孙树魁,张向东,等.热害矿井巷道温度场分布规律研究[J].中国地质灾害与防治学报,2003,14(3):9-11.

[10]秦跃平,党海政,刘爱明.用边界单元法求解巷道围岩的散热量[J].中国矿业大学学报,2000,29(4):403-406.

[11]吴强,秦跃平,郭亮,等.掘进工作面围岩散热的有限元计算[J].中国安全科学学报,2002,12(6):33-36.

(编辑徐岩)

Study on coupled transient temperature-thermal stress in deep roadways

LI Tiezeng1,WANG Li2,LI Yumei3

(1.Shandong Engineering Consulting Institute,Jinan 250013,China;2.School of Mining &Safety Engineering,Shandong University of Science &Technology,Qingdao 266590,China;3.Zoucheng Huajian Design Research Institute of Yankuang Group Company Limited,Zoucheng 273500,China)

This paper is aimed at investigating the coupled rules underlying temperature field and stress field of deep roadways.The investigation is performed by deducing the coupled transient thermal-elastic analytical solution of surrounding rock of circular roadway,analyzing the distribution rule of temperature field and thermal stress of surrounding rock of roadway,and identifying the influence of thermal stress on the stability of rock surrounding roadways by numerical simulations and in situ measurements.The results show that surrounding rocks occur with nonlinear changes in temperature distribution,the large gradient in surface layer ,and the smaller gradient in the depth;the increased ventilation time gives a gradual decrease in surrounding rock temperature,an increase in cooling ring,and a decrease in temperature gradient,thus tending to leave the temperature distribution curve quite gentle;the roadway ventilation allows such a change in the stress state of surrounding rock that the circumferential thermal stress occurs as tensile stress with the larger value in surface layer of surrounding rock and as compressive stress with the lesser value in the depth of surrounding rock of roadways;and the radial thermal stress,identified as tensile stress ,intensifies the extension depth of the plastic zone in roof and floor of roadways.

deep roadway;temperature field;thermal stress;ventilation

2015-02-09

李铁增(1968-),男,山东省临朐人,高级工程师,博士,研究方向:岩土工程、采矿工程的研究与咨询,E-mail:litiezeng@163.com。

10.3969/j.issn.2095-7262.2015.02.004

TD322;TD727

2095-7262(2015)02-0132-05

A