Sierpiski图与Sierpiski gasket图的条件着色∗
2015-11-02宋兴坤梁晓东
宋兴坤,梁晓东
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
(C1).若uv∈E(G),则c(u)=c(v);
(C2).∀v∈V(G),|c(N(v))|min{r,d(v)}.
可以正常(k,r)-条件着色的最小k称为G的条件色数,记为χr(G).
1 预备知识
定义1[3]
(i)ut=vt(t=1,2,···,h−1);
(iii)ut=vh和uh=vt(t=h+1,h+2,···,n).
设i∈{1,2,···,k},则顶点(i···i)叫做图S(n,k)的极点;图S(n+1,k)i是由图S(n+1,k)中标记为(i···)这样的顶点生成的,显然图S(n+1,k)i与图S(n,k)同构.
下面给出条件着色的一些性质与相关引理.
性质1[6]当图G是连通图,则下列条件保持成立:
(iv)如果图H是图G的一个子图,即H⊆G,则
引理1[6]如果所有度数大于1的点都在三角形中,则称图G是正规的,即
引理2[6]当n1,图Sn是唯一3可着色的.
引理3当图Sn的极点取相同颜色时,图Sn是唯一4可着色的.
证明当n=2时,极点取相同的颜色时,{1,2},{1,3},{2,3}组成K3,三点不能取与极点相同的颜色,图S2点着色c只有以下一种着色:c((11))=c((22))=c((33))=1;c({1,2})=2;c({1,3})=3;c({2,3})=4,如图2,所以图S2唯一4可着色.
假设n=k时,对图Sk结论都成立,当n=k+1时,因为图Sk与图同构,即则图的所有极点取相同的颜色时,图Sk+1是唯一可由图Sk的四种颜色着色.所有结论成立.
2 主要结果
定理1若n≥2,r≥1,则
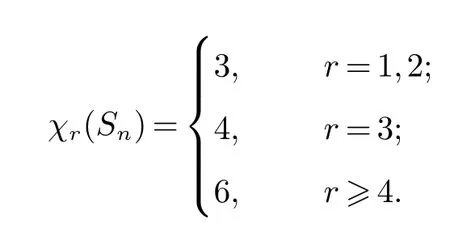
证明
(i) 当r=1时,由性质1-(i)与引理2,得χ1(Sn)=χ(Sn)=3;
(ii) 当r=2时,因为图Sn中任意边都在K3中,根据引理1,则有χ2(Sn)=χ1(Sn)=3;只需找到一种3点着色,如图1,c((11))=c({2,3})=1,c((22))=c({1,3})=2,c((33))=c({1,2})=3;显然这种着色一定是(3,2)-条件着色.
(iii) 当r=3时,根据性质1-(ii),χ3(Sn)4:
按引理3着色已经是4点着色,条件C1显然满足,下面证条件C2成立.
因图Sn极点是2度点,与其关联的顶点都取了不同的颜色;下面考虑任意度数大于3的顶点(即度数等于4)的邻点至少有3种颜色,在图S2中,{1,2},{1,3},{2,3}三顶点互为邻点,且都与极点相连,故这三点的邻点着色数等于3.图Sn是由数个S2组成的,只需考虑在图S2中是极点在图Sn中不是极点的点的邻集色数.即图S3中形如{12}这样的点,如图3,显然此点的邻集色数也是3.所以引理3的着色为(4,3)-条件着色.故当r=3时,χ3(Sn)=4.
(iv) 当r4时,根据性质1-(i),χr(Sn)=χ4(Sn).只需考虑r=4时的条件着色.
根据性质1-(ii),χ4(Sn)5.
当n=2时,图S2中(11),(22),(33),{1,2},{1,3},{2,3}六个顶点中,{1,2}与除了(33)的四个顶点相邻,图S2中除了(33)的五个顶点取不同的颜色:(11),(22)是{1,2}的两个相邻的顶点,故不能取相同的颜色,同理(11),(22),(33)都不能取相同的颜色,(33)与{1,3},{2,3}相邻,故不能取这两顶点颜色,又因(33)与{1,2}是{2,3}的邻点,也不能取{1,2}的颜色,所以(33)不能取与其他五个顶点相同颜色,也就是当图S2中六个顶点中都取不同的颜色时,此着色记为(6,4)-条件着色,又因6是可能的最小值,故χ4(S2)=6(如图4).
由性质1-(iv),χ4(Sn)χ4(S2)=6.
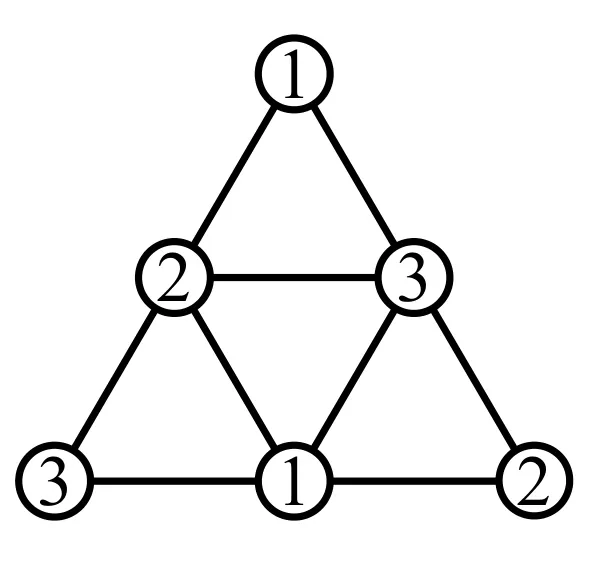
图1 χ2(S2)=3
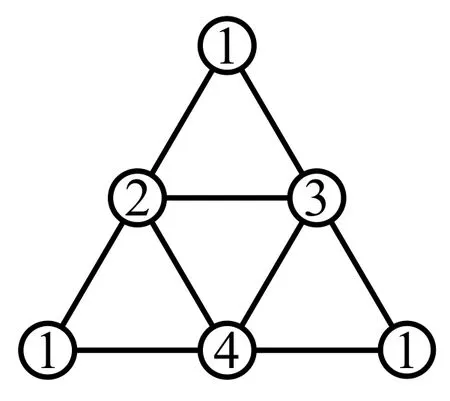
图2 χ3(S2)=4
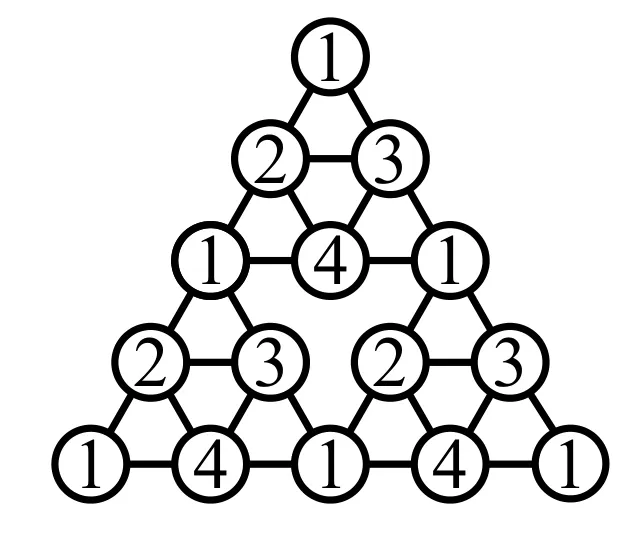
图3 χ3(S3)=4
当n=3时,令c((111))=1;c((222))=2;c((333))=6;c({1,2})=3;c({1,3})=5;c({2,3})=4;则(S2)i的极点都取不同的颜色,故内部点可由其余三种颜色着色.故S3可由S2的六种颜色着色.
设c是图Sn的一个r=4的条件着色,c(i···i)=x,(i∈{1,2,3};x∈{1,2,3,4,5,6}),这里x是极点(i···i)的颜色.
下面证明:当n是偶数时,存在一个条件着色c使得c(1···1)=1,c(2···2)=3,c(3···3)=5;当n是奇数时,存在一个条件着色c使得c(1···1)=1,c(2···2)=2,c(3···3)=6.
当n=2,3时,如图4,5,显然存在.
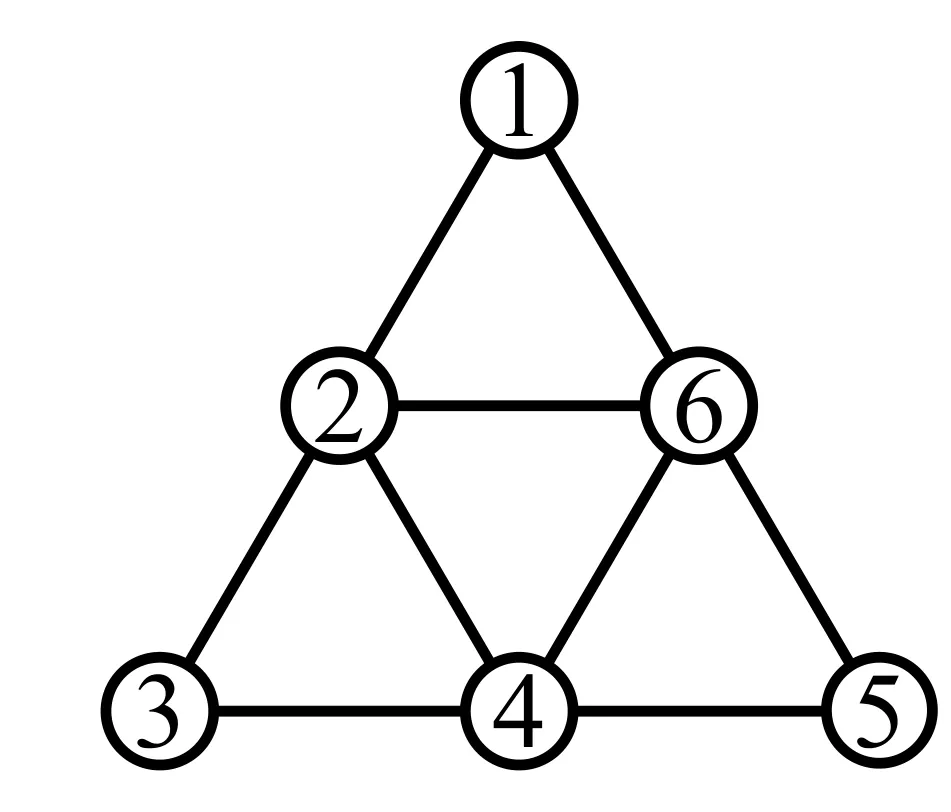
图4 χ4(S2)=6
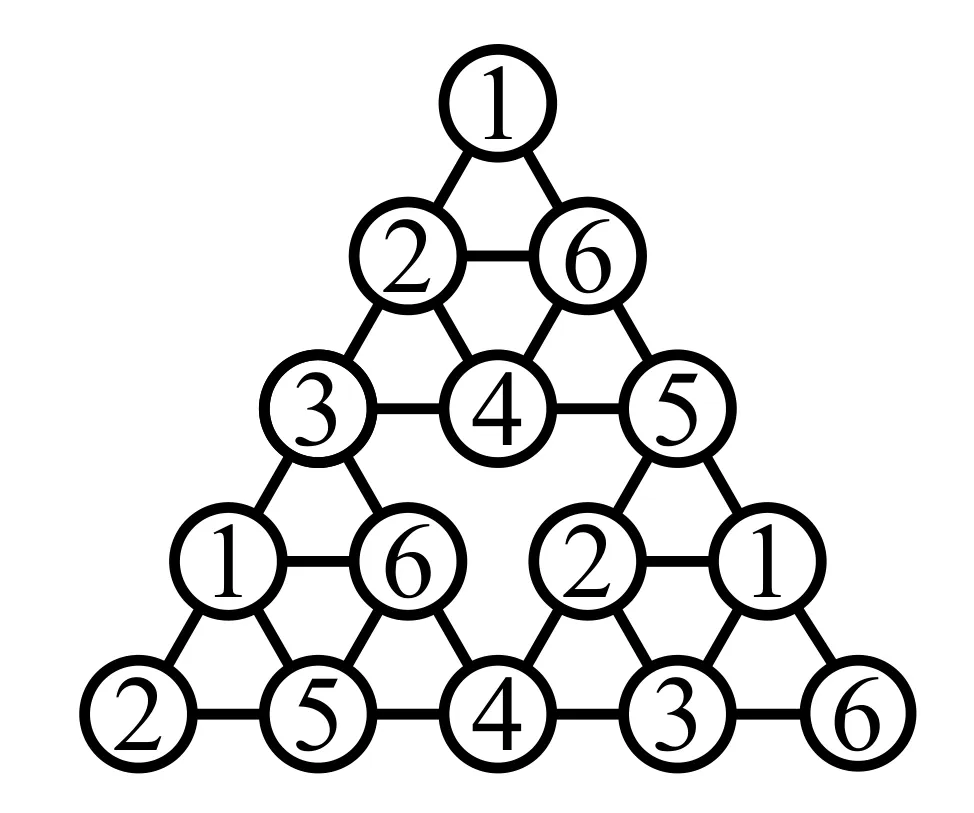
图5 χ4(S3)=6
当n是偶数时,Sn+1的着色如下:是Sn+1,1的着色,使得是的着色,使得综上,
当n是奇数时,Sn+1的着色如下:是Sn+1,1的着色,使得是Sn+1,2的着色,使得是Sn+1,3的着色,使得综上,
故Sn可由S2的六种颜色着色.
所以,当r4时,故χr(Sn)=6.
定理2若n≥2,r≥1,则
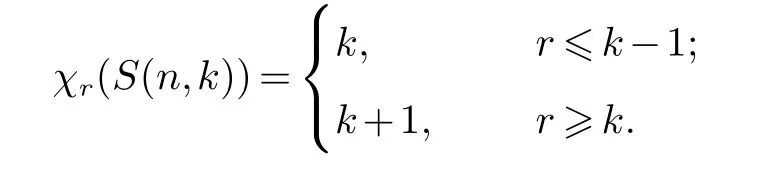
证明由S(1,k)=Kk,S(1,k)⊆S(n,k),又由性质1-(iii)(iv),则有
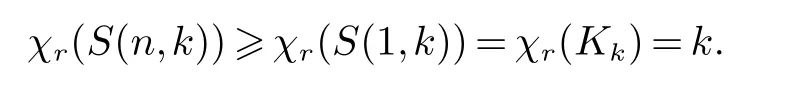
(i) 当rk−1时,设c是图S(n,k)一个着色,对∀(u1···un)∈S(n,k),令c((u1···un))=un;
下面证明:当rk−1时,图S(n,k)取该着色即为(k,r)-条件着色.
(a) 先证是正常着色,即条件C1:
图S(n,k)包含两类边,即∀uv∈E(S(n,k)),
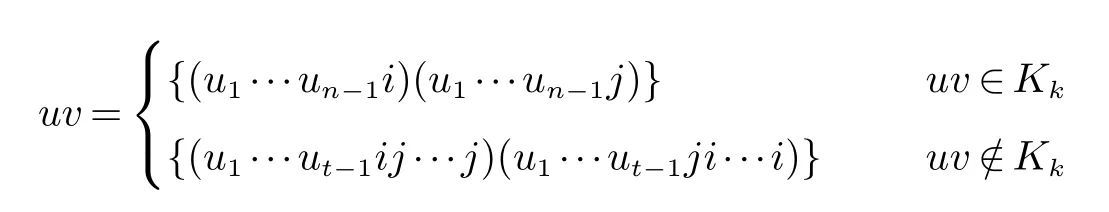
其中uk,i,j∈{1,2,···,k}.
当边在Kk中时,令c((u1···un−1i))=i,c((u1···un−1j))=j.
当边不在Kk中时,令c((u1···ut−1ij···j))=j,c((u1···ut−1ji···i))=i.
显然此着色是正常着色.
(b) 再证条件C2.因任意点v都在Kk中,Kk中的点取不同的颜色,v的邻点至少有k−1种颜色,故:|c(N(v))|k−1r,故(b)成立.
综合(a)(b),当rk−1时,图S(n,k)取上着色时为(k,r)-条件着色.又因k是满足条件最小的着色,故χr(S(n,k))=k.
(ii) 当rk时,因r∆,若要条件着色,只需将图S(n,k)的每个顶点的邻点都取不同的颜色.即
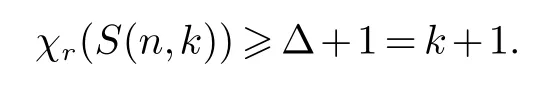
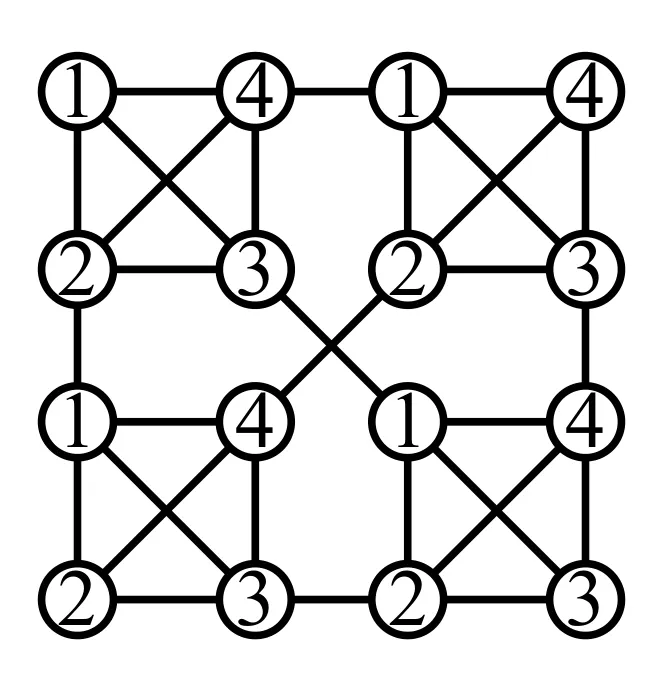
图6 χr(S(2,4))=4,r3
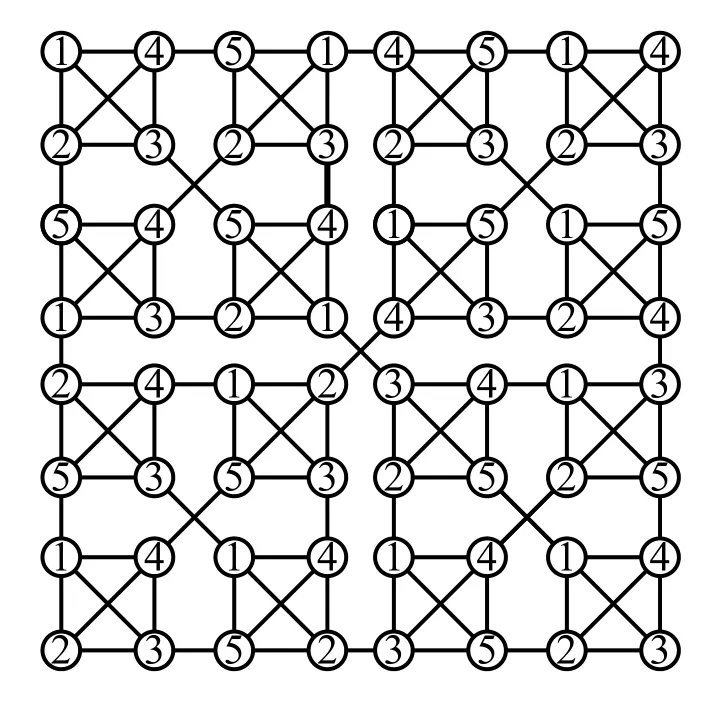
图7 χr(S(3,4))=5,r4
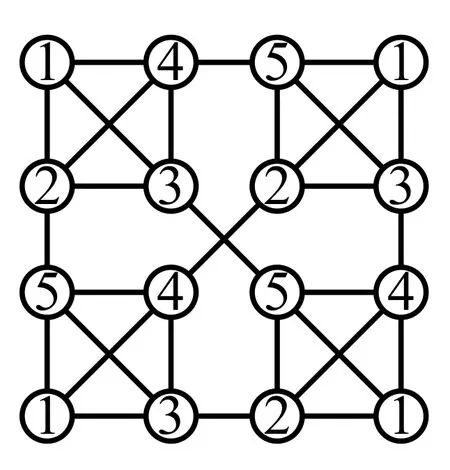
图8 χr(S(2,4))=5,r4
下面证明:图S(n,k)存在一个(k+1,r)-条件着色c.令
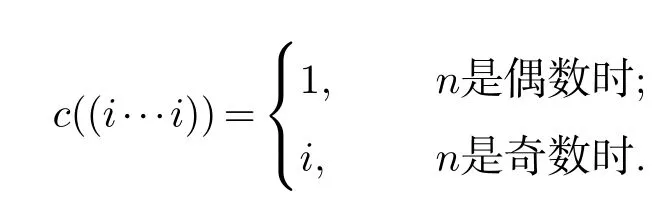
当n=2,对图S(2,k)进行着色,令c((ii))=1,c((h1))=k+1,c((ij))=j其中i∈{1,2,···k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i},则每个顶点的邻点的颜色都不同,即着色为(k+1,r)-条件着色.故χr(S(2,k))=k+1.
当n=3时,对图S(3,k)i,将图S(2,k)色数通过1→i,k+1→1,i→k+1(1)变换后,分别给图S(3,k)i进行此着色.则有c((iii))=c((ijj))=i,c((ijj))(),又c((jii))=j,图S(3,k)的所有点的邻点都取不同的颜色,故此着色都为(k+1,r)-条件着色.
当n是偶数时,假设在图S(n,k)中,令c((i···i))=1,c((h1···1))=k+1,c((ij···j))=j;i∈{1,2,···k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i}时,内部可(k+1,r)-条件着色.在图S(n+1,k)i中,将S(n,k)色数通过1→i,k+1→1,i→k+1(1)变换后,分别给图S(n,k)i进行此着色,则有c((i···i))=c((ij···j))=i(1,i}),c((ji···i))=j,故图S(n+1,k)存在(k+1,r)-条件着色.
当n是奇数时,假设在图S(n,k)中,令c((i···i))=c((ij···j))=i(j1,i}),若内部可(k+1,r)-条件着色.在图S(n+1,k)i中,将S(n,k)色数通过i→1,1→k+1,k+1→i(1)变换后,分别给图S(n+1,k)i进行此着色,则有c((i···i))=1,c((h1···1))=k+1,c((ij···j))=j,c((ji···i))=i;i∈{1,2,···,k},h∈{1,2,···k}/{1},j∈{1,2,···k}/{1,i},故图S(n+1,k)存在(k+1,r)-条件着色.
由此方法,图S(2,k)的(k+1,r)-条件着色可以推得图S(3,k)的(k+1,r)-条件着色,依次类推可以得到图S(n,k)的(k+1,r)-条件着色.
综上,当rk时,χr(S(n,k))=k+1.
