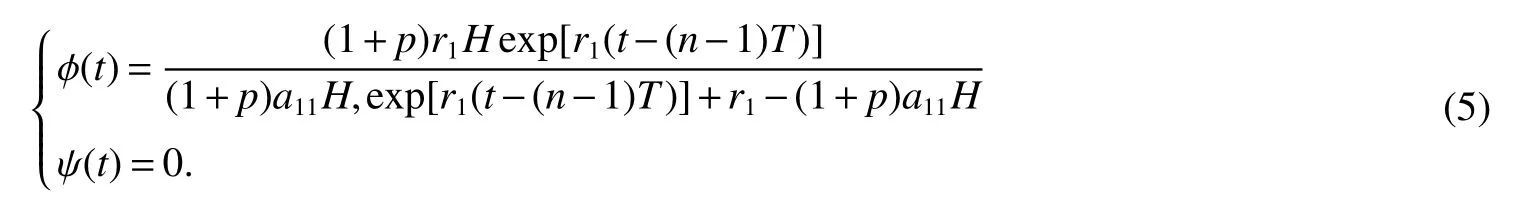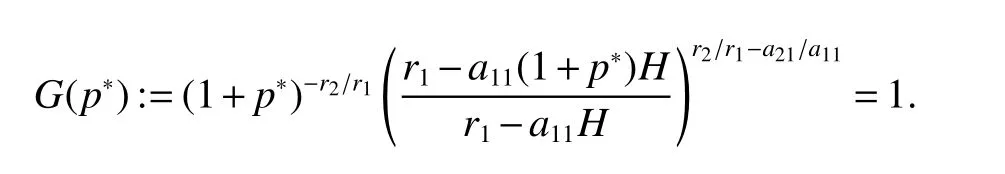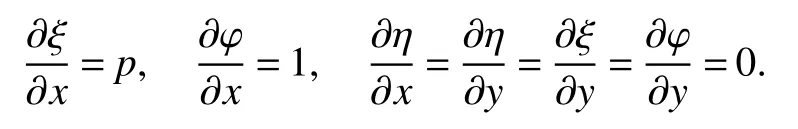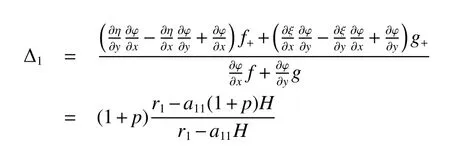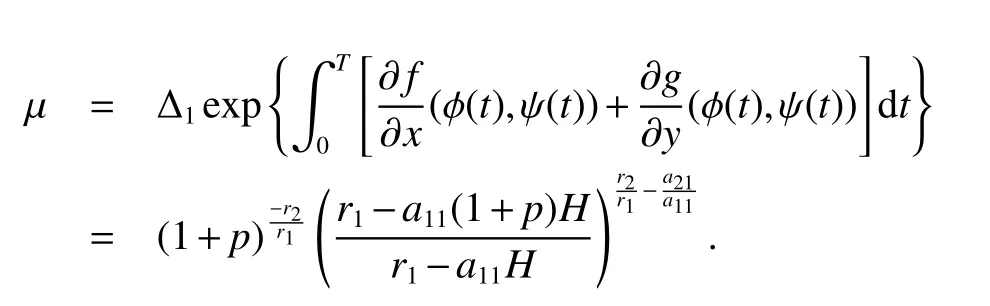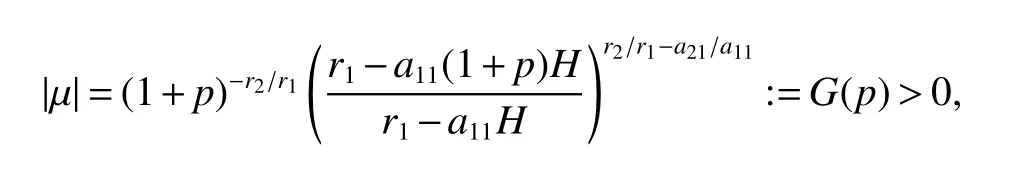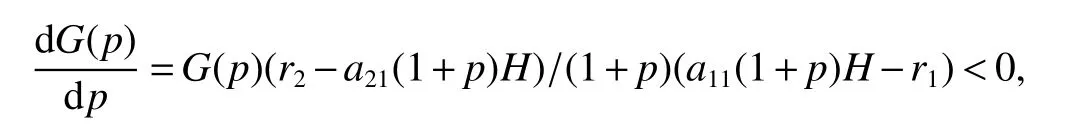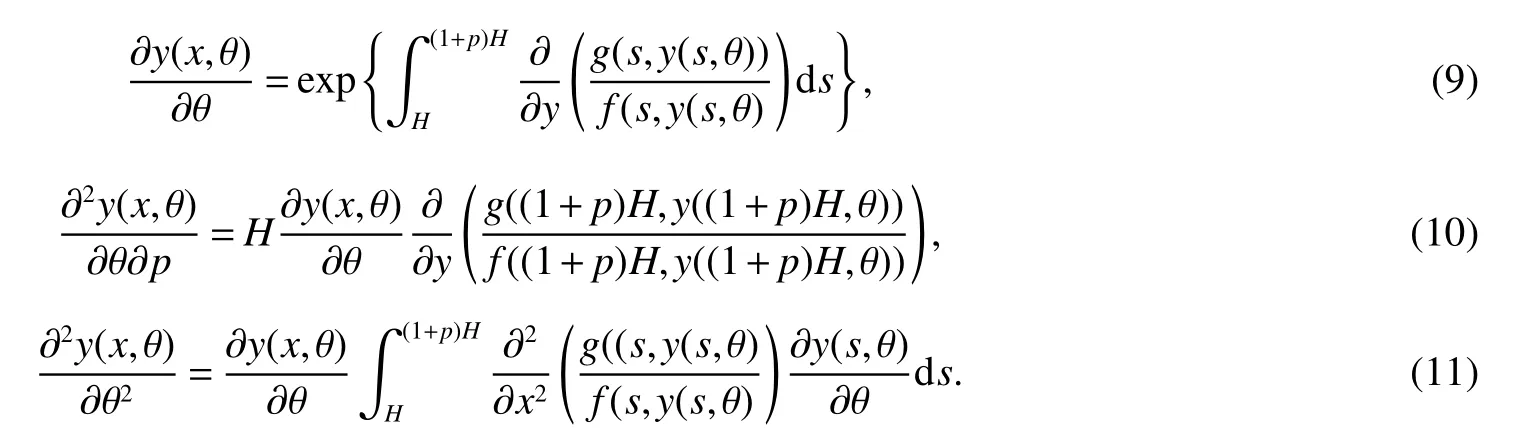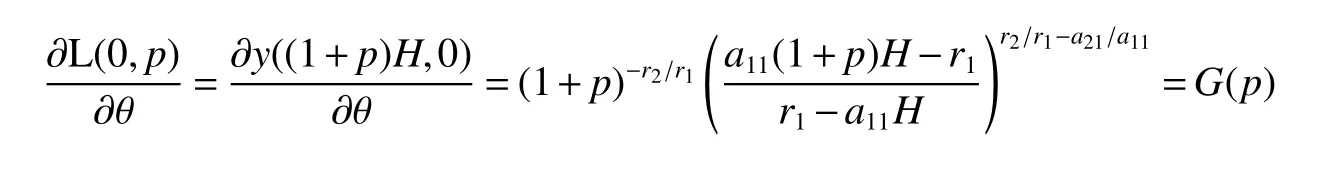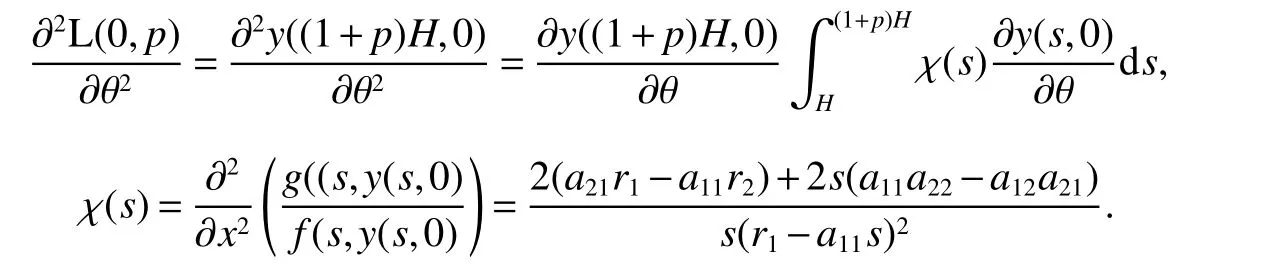Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗
2015-11-02HEZhilongNIELinfei
HE Zhi-long,NIE Lin-fei
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,a mathematical model of two-species competitive model with state-dependent impulsive replenish the endangered species is proposed,using the geometric theory of semi-continuous dynamic system and analogue of Poincar´e criterion,the sufficient conditions on the existence and orbital stability of positive order-1 periodic solution and semi-trivial periodic solution are obtained.
Key words:State-dependent impulsive control;Existence and stability;Periodic solution;Bifurcation
0 Introduction
Competition is a universal phenomenon in ecological communities due to the limitation of resources.In population dynamics,Lotka-Volterra competitive systems are ecological models that describe the interaction among various competing species and have been extensively investigated in recent years[1,2].By the principle of competitive exclusion,we can understand that only the dominant species survives when the competition between species is sufficiently strong.In order to prevent the the weaker species face extinction,the population of the weaker species should not under the reasonable value.Therefore,it is necessary to control the population of the weaker species should be remained the reasonable level.
It is well known that the ecological system is often affected by environmental changed and other human activities,such as vaccination,chemotherapeutic treatment of disease,chemostat,birth pulse,control and optimization.These discrete nature of human actions or environmental changes lead to population densities changing very rapidly in a short space of time.These short-time perturbations are often assumed to be in the form of impulses in the modeling process.Recently,the state pulse control has been widely applied in the predator-prey model due to its economic,high efficiency,and feasibility nature[3–6].Particular,Tang[7]introduced the predator-prey model with state dependent impulsive effects by poisoning the prey and releasing the predator,and analyzed the existence and stability of a positive period-1 solution by using the Poincar´e map,properties of the LambertWfunction or analogue of Poincar´e criterion.
Based on the above discussion,the main purposes of this paper is to present a dynamic model of two-species competitive with state dependent impulsive control strategy,and discuss the effect of the state dependent impulsive control to protect the endangered species.
The paper is organized as follows,some definitions and lemmas are provided in the next section.In Section 3,the existence,uniqueness and stability of a positive order-1 periodic solution of this model for two cases are stated and proved.Additional,we also discuss the transcritical bifurcation.
1 Model and Preliminaries
A classical autonomous Lotka-Volterra two-species competition model

wherex(t)andy(t)represent the population densities of the first and second species at timet,respectively.riis the natural growth rates,aiiis the co-efficients of intraspecific competition,denotes the degree to which the presence ofj−thspecies affects the growth ofi−thspecies.
It is easy to calculate that model(1)always has an unstable trivial equilibriumE0(0,0),a saddleE1(r1/a11,0)and a stable boundary equilibriumE2(0,r2/a22),and not positive equilibrium under the conditionr1/r2 (A1)When the density of speciesxdrops to the threshold valueHat timetk(H),we replenish(for example,artificial reproduction)some endangered speciesxat ratep∈(0,+∞). Based on the above assumption,we propose the following model From the biological background of model(2),we only consider the dynamical behavior of model(2)in region{(x,y):x≥0,y≥0}.We assume,throughout this paper,thatr1/r2 To discuss the dynamic behaviors of model(2),we define a impulsive setand a phase setwhereI:(x,y)∈Σ1→((1+p)H,y)∈Σ2is continuous function for anyP∈Σ1.HereIis called the impulse mapping. The following definitions and lemmas of model(2)are necessary throughout papers[3,6,8,9]. Definition 1For any pointXdefined as ΠP(t)=Π(P,t)is a continuous map such that:(a)Π(P,0)=Pfor allP∈X;(b)Π(Π(P,t),s)=Π(P,t+s)for allP∈Xandt,Then model(2)is called a semi-continuous dynamical system which is denoted by(X,Π,Σ1,I),and call ΠP(t)the trajectory passing through pointP. Definition 2Trajectory Π(P0,t)is called order-1 periodic solution with periodTif there is a pointP0∈ Σ2andT>0 such that Π(P0,t)=P∈ Σ1andI(P)=I(Π(P0,T))=P0∈ Σ2. Definition 3Suppose Π is an order-1 periodic solution of model(2).If for any ε >0,there must exists δ >0 andt0≥ 0,such that for any pointwe have the distanced(Π(P1,t),Π(P0,t))< ε fort>t0,then Π(P0,t)is orbitally asymptotically stable. Definition 4Supposeg:Σ2→ Σ2be a map.For anyP((1+p)H,yP)∈ Σ2,there exists at1>0 such thatis called the successor function of pointP,and the pointis called the successor point ofP. By the zero point theorem of continuous function in the closed interval,we have the following lemma. Lemma1[9]The successor functiong(P)is continuous.Further,model(2)exist a positive order-1 periodic solution if there exist two point Remark 1Obviously,ifg(P)=0,then the trajectory Π(P0,t)with initial pointP0is an order-1 periodic solution of model(2). Lemma 2[9]TheT-periodic solution(φ(t),ψ(t))of the system is orbitally asymptotically stable if the Floquet multiplier µ satisfies the condition|µ|<1,where andf,g,∂ξ/∂x,∂ξ/∂y,∂η/∂x,∂η/∂y,∂ϕ/∂xand ∂ϕ/∂yare calculated at the pointis the time of the j-th jump. Lemma 3[10]LetF:R×R→Rbe a one-parameter family ofC2map satisfying:(i)F(0,µ)=0;(ii)(∂F/∂x)(0,0)=1;(iii)(∂2F/∂x∂µ)(0,0)>0;(iv)(∂2F/∂x2)(0,0)<0.ThenFhas two branches of fixed points for µ near zero.The first branch isx(µ)=0 for allµ.The second bifurcating branchy(µ)=0.The fixed points of the first branch are stable ifµ<0 and unstable ifµ>0,while those of the bifurcating branch having the opposite stability. On non-negative solutions of model(2),we have the following lemma. Lemma 4Suppose that(x(t),y(t))is a solution of model(2)with initial valuesx(0+)≥0,y(0+)≥0,thenx(t)≥0 andy(t)≥0.Moreover,ifx(0+)>0,y(0+)>0,thenx(t)>0 andy(t)>0 for allt≥0. The proof of Lemma 4 is obvious,hence we omit here. In this section we will take into account the existence and stability of periodic solutions of model(2)in different case.Obviously,regionis divided into three different domains with isoclines dx/dt=0 and dy/dt=0 of model(2),where The following theorem is on existence and stability of positive order-1 periodic solutions with(1+p)H Theorem 1For anyp∈(0,+∞),we have (i)if(1+p)H (ii)ifH ProofWe first prove(i).Suppose that isocline dy/dt=0 intersects Σ1and Σ2at pointAandBrespectively.The trajectory ΠB(t)from the initial pointB((1+p)H,yB)reaches pointB1(H,yB1)on Σ1,next jumps to pointon Σ2,so pointis the success point ofB.However,from the geometrical construction of the phase regionit is easy to see that pointis located above pointB,that is,Therefore,the success function On the other hand,trajectory ΠA(t)starting from the initial pointA(H,yA)jumps to pointA+((1+p)H,yA)on Σ2due to the control strategies and reaches Σ1at pointA1(H,yA1)again.Further,ΠA(t)jumps to pointat Σ2.By the geometrical construction of the phase regionsobviously,pointis below pointA+,that is, Therefore,from Lemma 1,there exists a pointbetween pointsBandA+such thatSo,there exists a positive order-1 periodic solutionof model(2),initial pointof which is between pointsBandA+in set Σ2. Next,we discuss the uniqueness of positive order-1 periodic solution of model(2)for this case.Since the trajectories starting from pointsB0((1+p)H,yB0)(0 The setBA+is mapped to setby the geometrical construction ofandSubsequently,setB1A1is mapped to setby impulsive effects.From the geometrical construction ofit is easily to know thatline segmentssatisfyThis process is continuing,then we get sequencesof set Σ2satisfying and Now,we discuss its orbital stability.Fromit follows thatFor any pointwhere Without loss of generality,lettrajectory ΠC(t)starting from the initial pointCintersects Σ1at pointnext jumps to pointdue to the control strategies,whereRepeating the process,we obtain a sequenceSincethenwe also can getThus trajectory from initiating any pointCof Σ2which is between pointsBandA+ultimately tends to be the unique positive order-1 periodic solution From the above,we obtain that model(2)with(1+p)H Now we turn to(ii),that is,H Take another any pointS((1+p)H,yS)∈ Σ2satisfyingtrajectory ΠS(t)from the initial pointS((1+p)H,yS)reaches pointS1(H,yS1)on Σ1,next jumps to pointon Σ2,so pointis success point ofSand Therefore,we conclude that there exists a positive order-1 periodic solution of model(2),whose initial point is between pointsJ+andK+on Σ2.Similar to the proof of case(i),model(2)has a unique positive order-1 periodic solution and which is orbitally asymptotically stable forH Suppose thaty(t)=0 fort∈[0,∞),then model(2)is reduced to the following subsystem: Setx(0)=(1+p)H,then,by the first equation of(4),we obtainx(t)=r1exp(r1t)/(a11exp(r1t)+C),whereC=[r1−(1+p)a11H]/[(1+p)H].Letx(T)=H,thenx(T+)=(1+p)HandThis means that model(2)withr1/a11 On the stability of this semi-trivial periodic solution,we have the following result. Theorem 2For anyp∈(0,+∞)andr1/a11 ProofComparing with model(3),it is known thatf(x,y)=x(r1−a11x−a12y),g(x,y)=y(r2−a21x−a22y),ξ(x,y)=px,η(x,y)=0,ϕ(x,y)=x−H,(φ(T),ψ(T))=(H,0),and(φ(T+),ψ(T+))=((1+p)H,0).Therefore, and Furthermore,we obtain and In view ofr1/a11 byG(p)inpthe first derivative therefore,G(p)is a monotonically decreasing function inp.Thus,|µ|<1 whenp>p∗.Hence,(5)be a orbitally asymptotically stable.This completes the proof. Remark 2ForG(p∗)=1,a bifurcation may occur atp=p∗for|µ|=1,and a positive periodic solution may appear forr2/a21H−1 Now,we will discuss the bifurcation near the semi-trivial periodic solution.Consider the Poincar´e map of phase set Σ2as follows: From the bifurcation of map(6),we can obtain the following Theorem 3. Theorem 3A transcritical bifurcation occurs whenp=p∗.Therefore,a stable positive fixed point appears when parameterpchanges throughp∗from right to left.Correspondingly,model(2)has a unique stable positive order-1 periodic solution ifp∈ (r2/(a21H)−1,p∗). ProofFrom the geometrical construction of the regionsany trajectory ΠP(t)through the initial point((1+p)H,yP))∈ Σ1,whereyP:= θ ≥ 0,always reach Σ1at point(H,L(yP,p)).So,model(2)can be transformed as follows:, Let(x,y(x;x0,y0))be an orbit of system(7),and setx0=(1+p)H,y0:=θ≥0,then By(8)and the differentiability theorem of solution on initial condition,we have Next,we check whether the following conditions are satisfied. (a)Obviously, (b)From(9),we have which yields (c)From(10),we have Fromr1/a11 This means that(0,p∗)is a fixed point with eigenvalue 1 of the Poincar´e map(6). (d)Finally,by(11),we have By the assumptionr1/r2 It is easy to see that conditions(12)-(15)satisfy all conditions of Lemma 3.Thus,a transcritical bifurcation occurs whenp=p∗.Therefore,a stable positive fixed point appears when parameterpchanges throughp∗from right to left,and model(2)has a positive order-1 periodic solution forr2/(a21H)−1
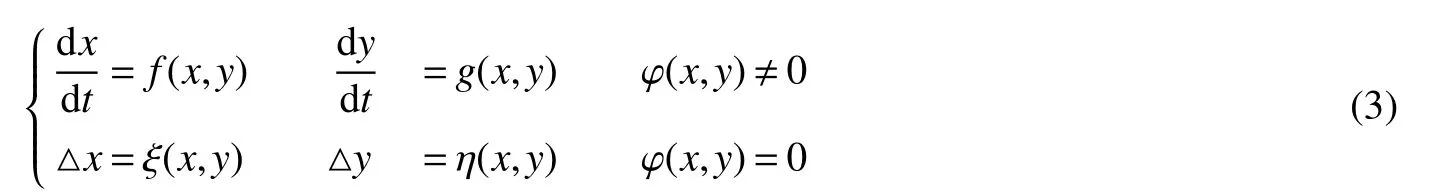

2 Main Results
2.1 The case of(1+p)H

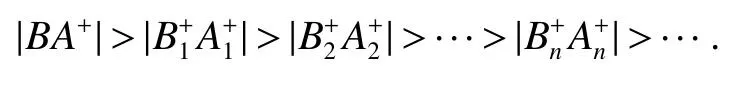

2.2 The case of r1/a11