汽轮机叶片曲面加工铣削力预测模型研究*

江 敏，谌永祥

（1.绵阳职业技术学院机电工程系，四川绵阳 621000；2.西南科技大学制造科学与工程学院，四川绵阳 621010）

汽轮机叶片曲面加工铣削力预测模型研究*

江 敏1，谌永祥2

（1.绵阳职业技术学院机电工程系，四川绵阳 621000；2.西南科技大学制造科学与工程学院，四川绵阳 621010）

文章针对汽轮机叶片曲面的加工特点，建立了铣削力模型，并从瞬时切削厚度的角度分析了数控工艺参数对铣削力模型的影响。在金属切削有限元模拟的基础上，运用Matlab和Abaqus软件结合四因素四水平正交模拟试验法验证了铣削力模型。并运用汽轮机叶片铣削加工实验进一步验证了铣削力模型和金属切削有限元模拟模型的有效性。

叶片曲面；铣削力模型；瞬时切削厚度；工艺参数；有限元

0 引言

汽轮机叶片是透平机械中起导流和能量转化作用的重要叶片类零件，它的汽道部分是由非均匀有理B样条曲线组成的自由曲面，其加工过程中受到切削力、切削振动、切削热的作用极易发生变形，而切削力是影响叶片曲面变形的主要因素之一［1］。建立接近实际加工状态的切削力预测模型，能够较有效地预测叶片曲面的变形量，进而优化切削参数以对其加工变形进行控制。谢小正［2］就汽轮机叶片铣削加工中存在的变形不易控制的问题，借助最小二乘支持向量机原理，建立了被加工不锈钢叶片表面的粗糙度预测模型。目前，国内外对于汽轮机叶片曲面的加工人为因素占较大比重，还不存在一个较为全面、可供参照的工艺参数设置来调节铣削力，建立它们之间相互关系的铣削力模型，实现从过程描述向过程预测发展，从静态预测向动态预测发展。

1 汽轮机叶片曲面加工特点

汽轮机叶片汽道由复杂的NURBS曲线拟合而成，加工过程中使用的是广泛用于加工自由曲面的球头铣刀。叶片曲面加工过程中，沿着刀具轴向刀刃，瞬时切削厚度不断变化。瞬时切削厚度对切削力的大小起着决定性的作用。同时，随着刀具的运动，刀具主轴与叶片法向之间的夹角发生变化，研究汽轮机叶片汽道型线曲率的变化，考虑刀具加工倾角对切削力的影响是必需的。切屑的形成是三维塑性变形过程，过去很多学者也做了不少研究，但都没有把影响瞬时切削厚度的各因素考虑周全。不同刀具不同切削加工方法，切削力计算模型也就不同。本文在球头铣刀切削力模型的基础上，综合考虑影响瞬时切削厚度的因素，同时根据汽轮机叶片曲面的加工特点建立切削力模型。

本文仅介绍汽轮机静叶片精铣叶片背弧面工序，其铣削加工过程如图1所示。

图1 汽轮机静叶片背弧面加工过程

加工过程可分析如下：

①在整个汽道型线加工过程中，工件处于一定角度，加工一侧叶片背弧面和叶缘，然后工件旋转一定角度加工另一侧叶片背弧面和叶缘。

②铣刀从进汽边进刀沿汽道截面型线向出汽边移动，然后从出汽边同样沿汽道截面型线向进汽边进行加工，刀具旋转方向不变。在通常的叶片加工工艺中，采用的是沿坡铣削方式，沿坡铣削又分为沿坡上铣削和沿坡下铣削［3］。当刀具为沿坡上铣时，刀具的进给方向为沿工件坐标系的x轴正向和z轴正向，当刀具铣削路径为沿坡下铣时，刀具的进给方向为沿工件坐标系的x轴负向和z轴负向。汽轮机叶片曲面的整个加工过程有上坡顺铣（1号路径）、下坡顺铣（1号路径）、上坡逆铣（2号路径）、下坡逆铣（2号路径），切削过程较为复杂。

③刀具倾角在加工过程中始终处于一个不变的角度，但是由于叶片汽道型线的曲率是变化的，故刀具和工件之间的加工倾角不断发生变化。

图2 汽轮机叶片加工受力图

叶片在剪切力和犁切力的共同作用下获得加工表面，剪切力和犁切力之和即为叶片受到的合力［4］。作用在叶片上的微元切向d Ft、径向d Fr、轴向d Fa切削力（图2b）可以表示为：

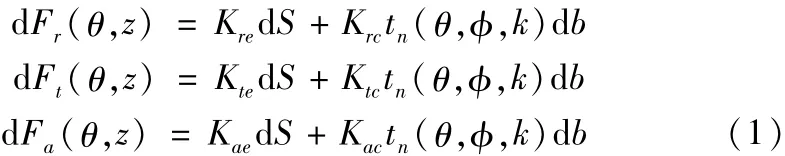
2 各参数对铣削力模型的影响

从铣削力预测模型可以看出，决定铣削力大小的因素有很多。有效切削刃的判定，即参与切削的切削刃微元段的数目及分布对切削力预测模型的准确性有很大影响；同时，球头铣刀切削微元的瞬时切削厚度是决定铣削力大小和方向的另一关键参数。瞬时切削厚度实际上是当前刀齿的切削路径和前一刀齿的切削路径在切削位置角的径向距离［5］。在铣削加工中，切削微元的瞬时切削厚度是刀具进给速度和切削位置角的函数。另外，刀具切削系统的变形，进给方向和大小，加工倾角的变化都在影响着瞬时未变形切削厚度的大小。

（1）进给量对切削力模型的影响

在叶片曲面的铣削过程中，刀具的进给运动是三维的，而且任意两个相邻走刀路径上的进给方向一般都不相同。因此，将进给速度限制在某一平面内是不合适的。在空间坐标系中定义刀具进给方向，它的方向和大小在坐标系各平面的投影关系如图3。

图3 进给方向描述

各方向进给量的关系式可表示为：

在切削刃上，切削微元段的切削半径可以表示为：

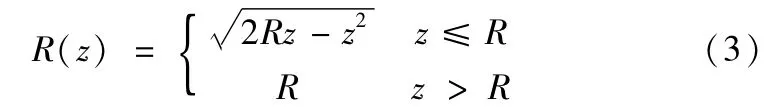
用切削刃上微元段的半径与y坐标之间的夹角ψ表示切削微元角度，以反应刀具转角位置。

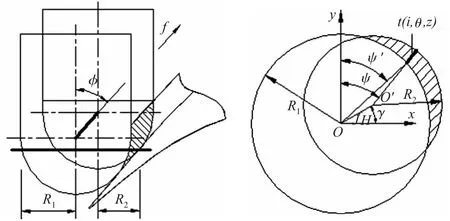
图4 三维进给运动下的瞬时切削厚度

由叶片曲面加工过程（图4）可以看出，汽轮机叶片曲面在加工过程中，随着走刀的进行，每齿进给量的水平投影发生了变化，同时当前切削刃微元段切除的不是上一微元段留下的材料［6］，即刀具在相邻切削位置的切削半径发生了变化，用R1表示当前步刀具切削半径，R2表示下一步切削半径，则

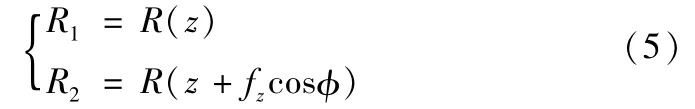
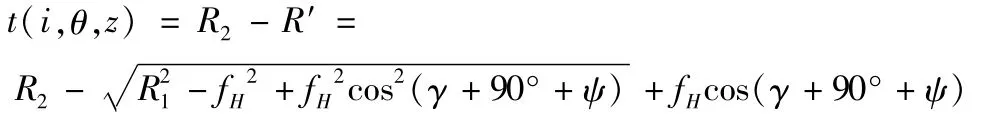
通常情况下，fH远小于R1，简化后的瞬时切削厚度为：

（2）刀具偏心和变形对切削力模型的影响

瞬时切削厚度是影响铣削力模型的一个重要参数。对于刚性较低的铣刀，切削力反作用在刀具上产生偏心，改变了刀具的加工路径，此时瞬时切削厚度也随着改变［7］。从图5可以看出，由于刀具的变形，球头铣刀刀尖位置z和z+fzcosφ处由铣削力作用变形后，轴心O和O＇和未变形前轴心C和C＇发生了偏离。此时，进给量从原来的CC＇变成了OO＇。

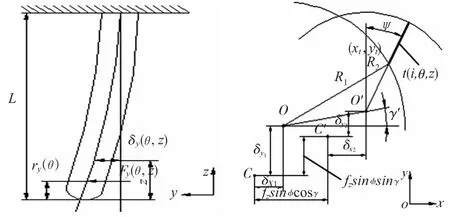
图5 考虑刀具变形的瞬时切削厚度示意图

刀具变形后的各项参数为：

用f＇H、γ＇分别代替fH、γ即可得到考虑刀具偏心和变形的瞬时切削厚度。

（3）加工倾角对切削力的影响

在叶片曲面沿汽道型线加工的过程中，刀具保持一定角度，刀具和工件表面的加工倾角随着叶片曲面曲率的变化而改变，如图6所示。垂直于叶片的力对叶片产生作用，一方面引起工件的回弹产生变形，另一方面若超过材料的弹性极限引起工件的挤压变形。将作用在叶片曲面上的三坐标力分解到垂直于叶片的法线方向，刀具加工倾角对力的大小起着决定性的作用。通过式（9）可以求得作用在曲面法线方向上的力F，根据该力的大小，可以反应叶片在加工过程中变形的情况，F越小，叶片变形越小。

图6 刀具与叶片加工倾角示意图

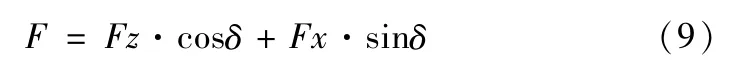
式（9）中，δ—球头铣刀的加工倾角，sinδ=（ac）/OP=（a-c）/ρ，ρ—曲线在点P的曲率半径。

（4）切削深度与宽度对切削力的影响

参与切削的微元切削刃数目和分布对于铣刀整体切削力有重要影响。对于任意一个微元切削刃P，要判断其在某一瞬时是否参与切削，需要5个判定条件［8］。同时用条件6对铣削力积分高度进行判定，结合前面5个条件即可计算出切削力。

球头铣刀铣削加工时，刀具与叶片的位置关系如图7，C为铣刀球头部分的球心，Pc为已知加工工件表面与铣刀球头部分的接触点，P为当前切削点，zp为当前切削点在铣刀坐标系o-xyz中的轴向高度，dn为已加工工件表面与未加工工件表面的距离，球心C在工件坐标系中的高度为ZC。

式（10）中，x、z—刀具坐标系下x、z轴方向单位向量，XPC—工件坐标系下Pc（刀具与已加工表面的接触点）点X坐标值。

条件1：0≤Xp≤L0，其中Xp=Xc+xp，xp= r（z） sin（φ（i，z）） ，L0是工件长度范围。

条件2：0≤Yp≤W0，Yp=Yc+yp，yp= r（z） cos（φ（i，z））。

其中，xp、yp—球头铣刀坐标系下P点的坐标值；Xc、Yc—工件坐标系下，球头铣刀球心在工件坐标系下的具体坐标；Xp、Yp—工件坐标系下P点的坐标值；W0—工件宽度范围。

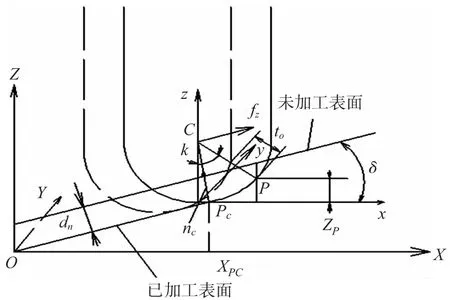
图7 刀具—工件切削模型

条件1、条件2表示：在工件坐标系下，当前加工点坐标位于工件大小范围内。

条件3：0≤Zp≤Zpm（X）p，Zp=Zc-R0+zp，Zpm（X）p=Xp tanδ，Xp=Xpc-R0sinδ-R0sin k。

其中，Zpm（Xp）—当前切削点P处相应的未加工表面的高度。

条件3表示当前切削点P的高度值小于相应位置处未加工表面的高度。

条件4：Lpc＞R（z），

其中，Lpc—当前切削点P与上次切削路径的距离；R（z）—上次切削路径中当z=zp时的有效切削半径；Δp—切削跨度。其中，

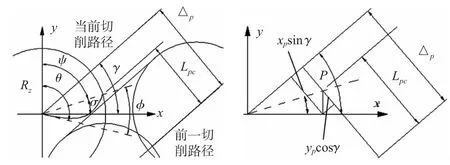
图8 当前切削点与上一切削路径的相对位置关系

条件4表示：当前切削点P在上次切削过程中未被切除，如图8所示。

条件5：t0＞0，其中，t0=fzer=fzxsinψjsin k+ fzycosψjsin k+fzzcos k

其中fz—每齿进给量；er—当前切削点P处铣刀包络线的法向向量。

条件6：对积分高度进行判定

参与切削的微元切削刃积分高度是计算球头铣刀整体切削力的关键参数，对其进行有效判定是正确计算切削力的基础。

①当切削深度在球头铣刀半径以下时（即ap≤R0-sinφ·R0），如图9。

积分上限为：z1=OF=R0-AF=R0-R0cosφ

②当切削深度在球头铣刀半径以上时（即ap＞R0-sinφ·R0），如图9。

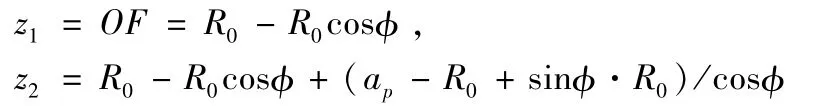
图9 有效切削刃积分高度判定

3 计算切削力的大小

加工过程中的铣削力对叶片曲面的加工变形有重要影响。将铣削力计算模型和各判定条件写入Matlab程序中，计算出汽轮机叶片曲面在加工过程中的切削力大小，其计算界面如图10。将其加工过程中的各工艺参数和加工状态参数输入到上述界面中，即可计算出切削力的值，用于后续的单因素研究和正交试验分析研究中，以开展切削参数对铣削力以及对汽轮机叶片曲面加工变形的影响研究。

图11 汽轮机叶片铣削加工有限元模型

4 铣削力模型的模拟验证

本文就数控工艺参数主要包括加工倾角、有效切削刃（切削深度、切削宽度）、每齿进给量（进给量）对汽轮机叶片曲面的铣削力模型展开研究。在对汽轮机叶片曲面铣削过程进行有限元建模时作出如下假设［9］，模型如图11所示。

（l）实际切削加工过程中前刀面粘结区刀具与切屑的摩擦系数是变化的，在有限元模型中假设前刀面与切屑的摩擦系数为恒定值；

（2）实际切削加工时，随着切削的进行刀具会有不同程度的磨损，而有限元模型中没有考虑刀具的磨损；

（3）实际铣削加工中不同的齿铣削时铣削力存在差异，在有限元模型中只是模拟单齿铣削过程。

上述结合汽轮机叶片曲面的加工特点建立了球头铣刀的铣削力模型，结合Matlab程序计算出加工过程中的切削力。为了验证铣削力模型的有效性，以金属切削有限元模拟的方式进一步模拟汽轮机叶片曲面的铣削过程，得出铣削力大小。现对两种方式所得结果进行对比分析，表1给出了铣削力预测模型的切削力大小与切削有限元模拟的铣削力大小的对比结果，第七列列出了预测值与模拟值的相对误差，能够很清晰地看出预测值和模拟值的吻合度。

表1 铣削力预测值与模拟值相对误差分析表

由表1和图13可以看出：

（1）切削力预测值与模拟值大小最大误差为91.55%，最小误差为-4.15%；

（2）切削力预测值与模拟值大部分吻合，变化趋势基本一致，平均误差为6%。

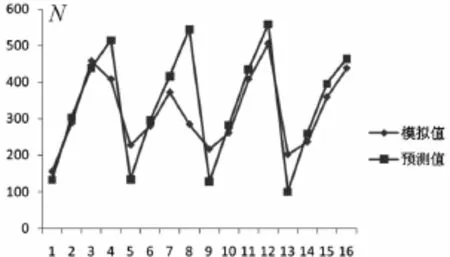
图13 铣削力预测值与模拟值对比图

5 铣削力模型实验验证

为了进一步验证上述铣削力模型的正确性，本文就上述4个参数（加工倾角、切削深度、切削宽度、每齿进给量）进行了汽轮机叶片铣削加工实验，实验结果如表2所示。

图14 汽轮机叶片加工图

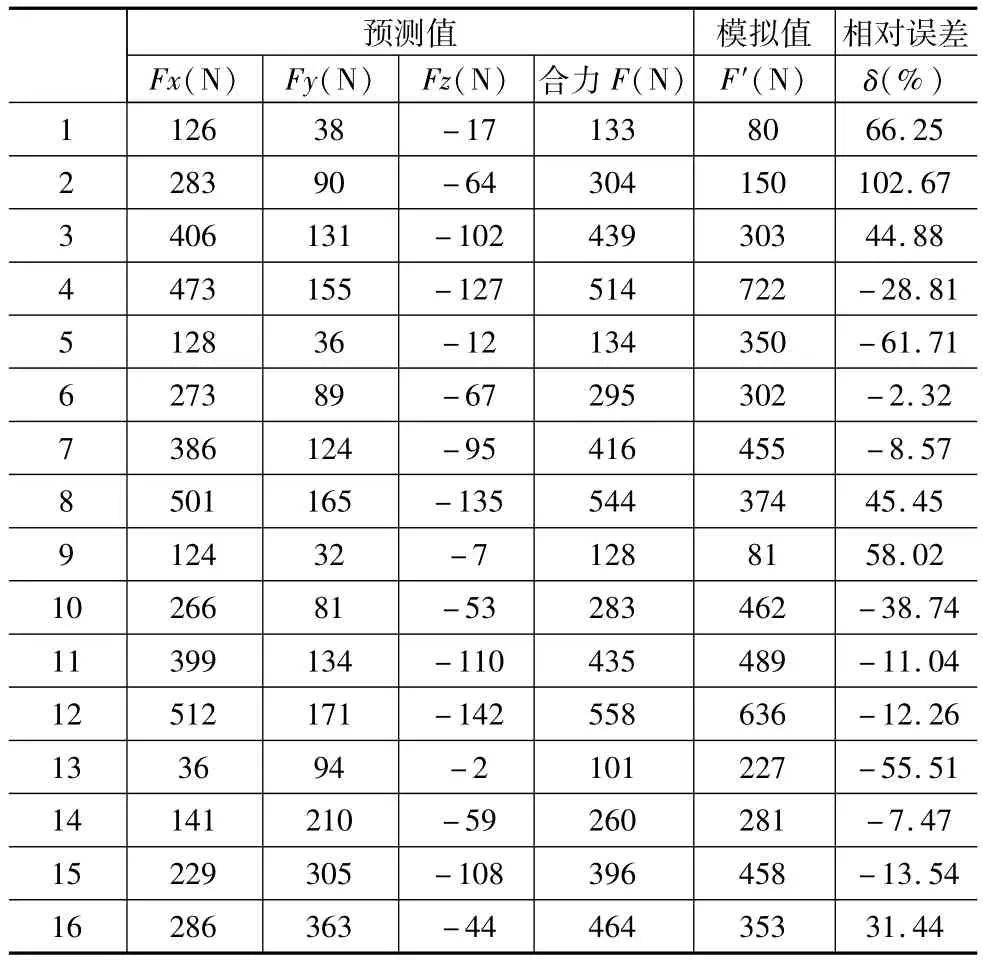
表2 铣削力预测值与实验值相对误差分析表

图15 铣削力预测值与实验值对比图

由表2和图15可以看出：

（1）切削力预测值与实验值大小最大误差为102.67%，最小误差为-2.32%；

（2）切削力预测值与实验值大体吻合，平均误差为6.8%。

通过切削力预测值与切削力有限元模拟值的结果分析对比和切削力预测值与切削力实验值的结果分析对比，可认为本文提出的铣削力预测模型基本有效，模拟结果相对比较合理。产生误差的原因主要是金属切削有限元模拟模型简化，忽略了切削热、振动等一些因素的影响，以及实际加工中切削液的使用对切削力的影响。

6 小结

（1）结合汽轮机叶片曲面的加工特点，针对数控工艺参数对瞬时切削厚度的影响，建立了适用于汽轮机叶片曲面的铣削力模型。

（2）运用金属切削有限元理论对其进行验证，切削力模型预测值与金属切削有限元模拟值基本吻合，该铣削力模型基本有效。

（3）运用金属切削实验对各参数对切削力大小的影响进行了实验验证，认为本文所建立的金属切削有限元模拟模型合理，基本有效。

［1］赵威，何宁，李亮.薄壁结构的高效铣削加工［J］.航空精密制造技术，2002，38（6）：12-15.

［2］谢小正，赵荣珍，陈惠贤.基于LS-SVM的汽轮机叶片高速铣削表面质量预测建模［J］.机械制造，2012，50（10）：73-75.

［3］Fontaine M，Moufki A，Devillez A，et al.Modeling of cutting forces in ball-end milling with tool-surface inclination partⅠ：prediction force model and experimental validation［J］. Journal of Materials Processing Technology，2007，189（1-3）：73-84.

［4］P.L，Y.A.Prediction of Ball-End Milling Forces From Orthogonal Cutting Data［J］.Elsevier Science，1996，36（9）：1059-1072.

［5］O E E K Omar，T El-Wardanyc，E Ngb，et al.An improved cutting force and surface topography prediction model in end milling［J］.International Journal of Machine Tools&Manufacture，2007，47：1263-1275.

［6］Lim EM，Feng H Y，Menq CH，et al.The prediction of dimensional error for sculptured surface productions using the ball-end milling process.Part1.Chip geometry analysis and cutting force prediction［J］.Int J Mach Tools Manufact，1995，35（8）：1149-1169.

［7］杨胜培，钟志华，尚振涛，等.考虑刀杆柔性的球头铣刀切削力模型的研究［J］.中国机械工程，2007，18（5）：545-568.

［8］王启涛，刘战强，汤爱民，等.球头铣刀瞬态切削力数学模型建立与仿真［J］.农业机械学报，2011，42（8）：200-206.

［9］McDill，JM J，Lindgren，et al.Continuous improvement in thermal-mechanical finite element analysis.International Conference on Processing and Manufacturing of Advanced Materials，Lasvegas，USA，2000：4-8.

The Research of Milling Force Prediction Model Suitable for Turbine Blade Surface Machining

JIANG Min1，CHEN Yong-xiang2
（1.Department of Mechanical and Electrical Engineering，Mianyang Vocational and Technical College，Mianyang Sichuan 621010，China；2.School of Manufacturing Science and Engineering，Southwest University of Science and Technology，Mianyang Sichuan 621010，China）

Based on the characteristics of the turbine blade surface processing，milling force model is established.From the perspective of the instantaneous cutting thickness，the relationship between the numerical process parameters and the milling force model is analyzed.On the basis of finite element simulation of metal cutting，using Matlab and Abaqus combined with four factors and four levels orthogonal simulation test method，the effectiveness of the milling force model has been verified.Turbine blade machining experiment has been used to further verify the Validity of the milling force model and the metal cutting finite element simulation model.

blade surface；milling force model；instantaneous cutting thickness；numerical process parameters；FEM

TH165；TG659

A

1001-2265（2015）03-0129-05 DOI：10.13462/j.cnki.mmtamt.2015.03.035

2013-11-30；

2014-08-26

四川省科技支撑计划项目：基于智能化补偿与网络自适应控制的超精密数控加工研究（2010GZ0135）

江敏（1988—），女，四川隆昌县人，绵阳职业技术学院教师，工学硕士，研究方向为先进制造技术，（E-mail）jianmin1516@163.com。