高速铣削TC4表面粗糙度预测模型研究*

张宝磊，熊艺文，王为庆，朱帅玲

（桂林航天工业学院a.建筑环境与能源工程系；b.机械工程系，广西桂林 541004）

高速铣削TC4表面粗糙度预测模型研究*

张宝磊a，熊艺文a，王为庆b，朱帅玲b

（桂林航天工业学院a.建筑环境与能源工程系；b.机械工程系，广西桂林 541004）

零件表面粗糙度的影响因素具有复杂性和不确定性，切削参数是能够人为控制并对零件的表面质量有较大影响的因素之一。为了优选合适的切削参数以达到提高零件表面加工质量的目的，通过设计正交试验并在此基础上建立了钛合金TC4高速铣削表面粗糙度的GRNN广义回归神经网络预测模型和经验回归模型，对其预测误差进行了比较分析。结果表明：所建立的GRNN预测模型较回归预测模型有更高的预测精度，能够更好的对表面粗糙度进行动态控制。

GRNN；预测；粗糙度；TC4

0 引言

零件表面粗糙度是衡量零件表面质量的重要参数，长期以来一直是学者们研究的重点内容之一，它对工件的疲劳强度、接触刚度、耐腐蚀性能、工件精度都有重要的影响［1］。高速加工做为一种先进制造技术，在模具加工、医疗、航空等行业有较多应用，但是切削参数的选择一直是困扰行业的一个难题［2］。目前，遗传算法、模糊控制以及神经网络等人工智能技术逐渐成为机械加工中优选切削参数以及预测加工效果的重要方法［3-8］。GRNN神经网络具有较强的局部逼近能力和较快的学习速度，需要人为调节的参数较少，可以最大限度地避免人为的主管假定对预测结果的影响的优点，因此得到广泛的应用［9-11］。本文利用正交实验设计方法安排了铣削实验，并选择合适实验参数建立了高速铣削TC4粗糙度的GRNN广义回归神经网络预测模型和经验回归模型，通过比较分析两种预测模型的预测误差来验证所建立的GRNN预测模型的正确性以及预测效果的准确性。

1 实验条件及方案

1.1 实验条件

本实验是在Mikron UCP-710五轴加工中心（最高转速42000rpm）采用硬质合金TiAlN涂层刀具（直径D=4mm）高速铣削加工TC4钛合金。粗糙度仪采用Taylor surf 60表面粗糙度测量仪测量五次取算术平均值。

1.2 实验方案

影响零件加工表面粗糙度的因素有很多，本实验在忽略机床主轴振动以及刀具磨损等因素的情况下，主要研究切削参数的变化对零件表面粗糙度的影响（如表1），为了减少实验次数，本文利用正交实验表L16（45）安排铣削实验，试验结果如表2。依据检测结果建立粗糙度值的GRNN神经网络模型和回归经验预测模型。

表1 试验参数表

表2 L16（45）正交试验设计及测试结果表

2 GRNN广义回归神经网络的创建与训练

2.1 GRNN广义回归神经网络原理

GRNN广义回归神经网络是由径向基神经元和线性神经元组成，这种形式的网络常用于函数逼近，其网络结构如图1所示。该网络的第一层为径向基隐含层，神经元个数等于训练样本个数，该层的权值函数为欧氏距离函数（用‖dist‖）表示，其作用为计算网络输入与第一层的权值IW1，1之间的距离，b1为隐含层的阈值。符号“·”表示‖dist‖的输出与阈值b1之间的关系。隐含层的传递函数为径向基函数，通常采用高斯函数作为网络的传递函数如式（1）所示：

其中，σi决定了第i个隐含层位置中基函数的形状，σi越小，网络对样本的逼近性能就越强；σi越大函数越平滑，所以又称为光滑因子。

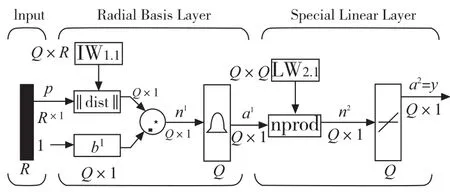
图1 GRNN回归神经网络模型

网络的第二层为线性层，其权函数为规范化点积权函数（用nprod表示），计算网络的向量n2，它的每个元素就是向量a1和权值矩阵LW2，1每行元素的点积再除以向量a1的各元素之和得到的，并将结果n2提供给线性传递函数a2=purelin（n2），计算网络的输出［12］。

2.2 广义回归神经网络粗糙度预测模型的创建与训练

根据本试验对TC4高速铣削表面粗糙度的影响因素进行分析，这里取切削参数（主轴转速N、径向切深Ae、轴向切深Ad和每齿进给量fz）作为对表面粗糙度的影响因子，以粗糙度值作为输出因子，即网络的输出。由于其中的各项指标都不同，原始数据中各向量的数量基差别比较大，为了计算方便以及防止部分神经元达到饱和状态，在输入中对样本采用公式（2）进行归一化处理。

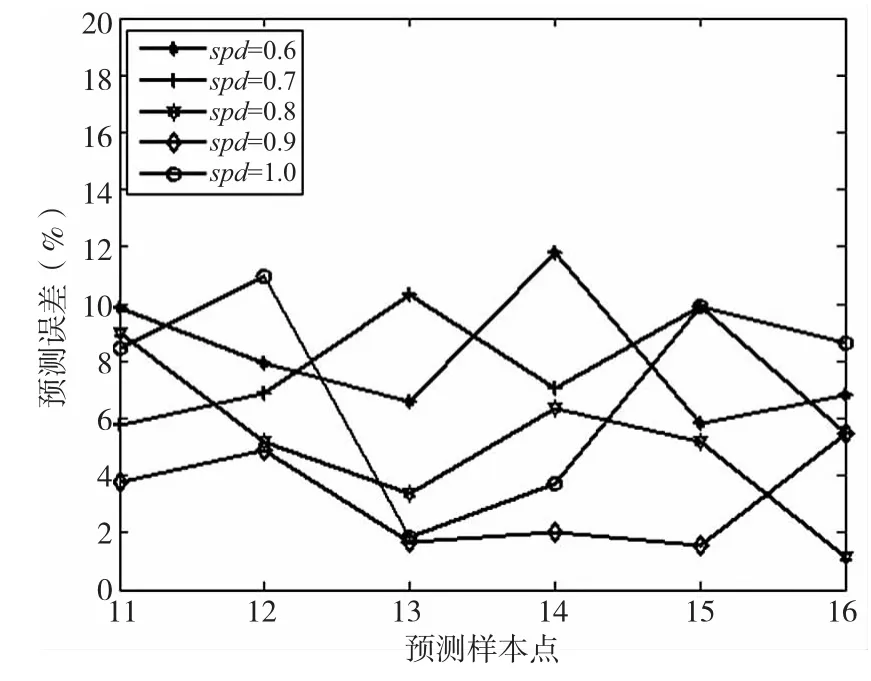
图2 网络的预测误差

根据正交试验表，本文安排其中的前十组试验参数作为网络的训练样本，其余的六组作为外推预测样本，如表2所示。GRNN回归神经网络不同于BP神经网络，其建立网络的过程也就是训练的过程，所以直接建立的net即是训练好的网络。由此构建GRNN网络，由于光滑因子也可以影响网络的性能，经过优选后，本文所建立的GRNN广义回归网络从0.5、0.6、0.7、0.8、0.9、1中进行比较选择，预测效果如图2所示，由图可见当光滑因子为0.9时误差比较小，都在5%左右。

3 表面粗糙度的经验回归预测模型

回归经验模型常用来确定两个或两个以上变量对目标的定量关系，是一种常用的数理统计方法，广泛用于生产中的预测和控制。本文建立多元回归经验模型预测与GRNN预测模型检验样本同样切削参数条件下的粗糙度，通过比较两种预测模型的误差来验证所建立的GRNN预测模型的可靠性。同时对回归经验模型预测进行了显著性检验，其呈高度显著性。

在忽略机床主轴刚度以及刀具磨损对表面粗糙度的影响，建立粗糙度与切削用量的指数形式回归表达式（3）：

为了检验所建立的回归方程的逼近性能，需要对其进行显著性检验，本文采用广泛应用的F-检验。假设：

其中QE是回归平方和，Q是残差平方和，n是试验组样本数，p是独立变量的个数（p=4）。检验结果如表3所示。

表3 显著性检验分析表

依据数理统计可得：

Jα=｛F＞Fα（p，n-p-1）=F0.05（4，11）= 3.36｝，所以子样落入拒绝域。说明所建立的回归模型具有较高的显著性，能够很好的模拟实际加工情况，可以用于预测本条件下的工件粗糙度。

4 广义回归神经网络与多元线性回归误差比较

用广义回归神经网络检验样本输出结果与多元线性回归结果比较相对误差如下表：

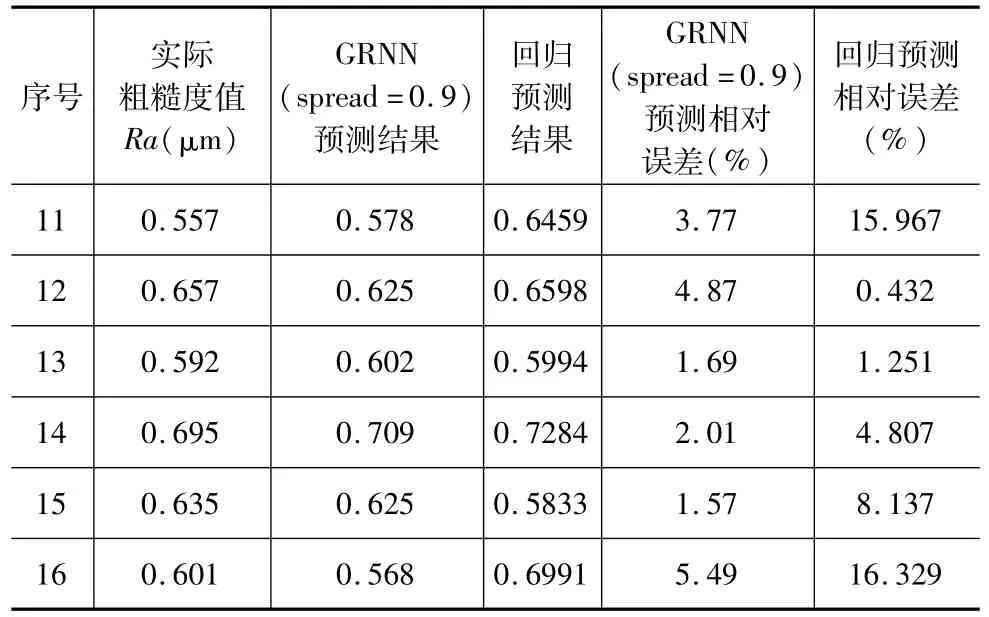
表4 误差分析表

从表4中可以看出建立的GRNN广义回归神经网络预测模型（spread=0.9）预测误差除了最大的5.49%之外都集中在5%以内，可以较好的预测本实验条件下的表面粗糙度，而回归经验预测模型的预测误差则相对比较分散但也都集中在20%以内，通过比较两种预测模型误差可以看出所建立的GRNN预测模型预测结果具有较高的准确性，能够较好的指导工程实践，可以摆脱从大量的试验数据来研究切削参数对表面粗糙度的影响规律，节约试验成本，有一定参考价值。

5 结论

（1）利用广义回归神经网络具有训练速度快，能以较少的实验数据得出较高的预测结果的优点，本文建立了GRNN广义回归神经网络来预测TC4高速铣削时的表面粗糙度，预测误差较小，基本上都集中在5%左右，可以指导实际生产的参数选择。

（2）当光滑因子取0.9时所建立的GRNN预测模型的预测误差最小。

（3）建立多元回归经验模型，通过比较其与GRNN回归神经网络预测误差来说明GRNN的可靠性，防止采用单一的预测模型出现主观误差。

［1］张利堂.基于正交试验的高速铣削表面质量研究［J］.机床与液压，2014，42（1）：80-103.

［2］查文炜，何宁.高速铣削淬硬钢刀具磨损机理的研究［J］.机械设计与制造，2008（12）：220-222.

［3］王素玉，艾兴，赵军，等.高速铣削表面粗糙度建模与预报［J］.工艺与检测，2006（8）：65-68.

［4］曹宏瑞，陈雪峰，何正嘉，等.主轴-切削交互过程建模与高速铣削参数优化［J］.机械工程学报，2013，49（5）：161-166.

［5］Franci Cus，Uros Zuperl.Approach to optimization of cutting conditions by using artificial neural networks［J］.Materials Processing Technology，2006（173）：281-290.

［6］Durmus Karayel.Prediction and control of surface roughness in CNC lathe using artificial neural network［J］.Materials Processing Technology，2009（209）：3125-3137.

［7］Wang zongrong，Zuo dunwen，Wang Min.Fuzzy orthogonal optimization for high speed milling parameters of milling TC4［J］.Journal of Nanjing University of Science and Technoloy，2005，29（6）：709-712.

［8］Sardinas RQ，Santana M R，Brindis E A.Genetic Algorithmbased Multi-objective Optimization of Cutting Paramet-ers in Turning Processes［J］.Engineering Applications of Artifical Intelligenc，2006，19（2）：127-133.

［9］Karpat Y，Ozel T.Multi-objective Optimization for Turing Processess Using Neural Network Modeling and Dynam-ic-neighborhood Partical Swarm Optimization［J］.Int.J.Ad-v. Manuf.Technol，2006，21：203-217.

［10］LEE W Y，HORSE JM，KYONG N.Subsytem level fault diagnosis of a building’s air-handling unit gengral regression neural networks［J］.Applied Energy，2004，77（2）：153-170.

［11］李朝将，凡银生，李强，等.基于GRNN的电火花线切割加工工艺预测［J］.华中科技大学学报（自然科学版），2012，40（增Ⅱ）：1-4.

［12］飞思科技产品研发中心.神经网络理论与MATLAB 7实现［M］.北京：电子工业出版社，2005.

（编辑 李秀敏）

Research on Surface Roughness Prediction Model for High-SPeed Milling TC4

ZHANG Bao-leia，XIONG Yi-wena，Wang Wei-qingb，Zhu Shuai-lingb
（a.Department of Constructs Environment and Energy Engineering；b.Department of Mechanical Engineering，Guilin College of Aerospace Technology，Guilin Guangxi541004，China）

The factors influencing the workpiece surface roughness is complexity and uncertainty，the cutting parameters are one factor of ones that have great influences on machined surface quality which can be controlled artificially.In order to choose appropriate cutting parameters to get better machined surface quality，the paper design orthogonal experimental and establish TC4 Empirical regression prediction model and generalized regression neural networks（GRNN）for prediction of surface roughness when high speed milling TC4 and compare the predicting error.Results show that the established GRNN prediction mode has better prediction precision which can be used to control the surface roughness dynamically.

GRNN；prediction；surface roughness；TC4

TH16；TG506

A

1001-2265（2015）03-0108-03 DOI：10.13462/j.cnki.mmtamt.2015.03.029

2014-07-12；

2014-08-16

桂林航天工业学院院级基金项目（YJ1307）

张宝磊（1982—），男，河南漯河人，桂林航天工业学院讲师，硕士，研究方向为先进制造及其智能检测，（E-mail）zblei@guat.edu.cn。