基于PRO/E与ADAMS二级行星齿轮传动系统的动力学研究*

张学军，郭俊超

（东北电力大学机械工程学院，吉林吉林 132012）

基于PRO/E与ADAMS二级行星齿轮传动系统的动力学研究*

张学军，郭俊超

（东北电力大学机械工程学院，吉林吉林 132012）

多级行星轮系结构复杂，运动学与动力学的表现难以确定。文章以二级行星齿轮传动系统为研究对象，确定太阳轮、行星轮与内齿轮之间正确的啮合参数，利用三维造型软件PRO/E建立行星齿轮传动系统的实体模型，以动力学分析软件ADAMS为平台建立虚拟样机模型，进行传动系统的运动学与动力学仿真。仿真得到系统的传动比、输出轴的输出速度以及齿轮之间的径向力与圆周力，结果与理论计算结果吻合度很高，说明虚拟样机模型的构建合理。仿真结果可对多级行星齿轮减速器的优化设计和工程分析提供理论依据。

二级行星轮系；虚拟样机；碰撞；动力学仿真

0 引言

与普通定轴齿轮传动相比，行星齿轮传动最主要的特点就是至少有一个齿轮的轴线是动轴线，因而称为动轴轮系。该种传动方式采用功率分流，使用数个行星轮来分担载荷，并且应用内啮合的咬合方式。这种合理的均载装置使行星传动具有以下重大优点：质量轻、体积小、传动比范围大、承载能力不受限制、进出轴线呈同一轴线，同时传动效率较高。在国外，行星齿轮减速器应用已极为普遍，各国均有系列产品，并已大量生产，尤其是在高速大功率传动与低速重载方面不断取得重大突破。以德国DEMAG的一种行星减速器为例，该减速器承载能力已高达54600kW，对应的输出轴最大扭矩（峰值）约2400kWm；最大传动比已达5000。我国近年在行星齿轮减速器方面也已有很大的发展与提高，主要用在矿山机械、起重运输、船舶工业、机械工程、鼓风机、风力发电等设备上［1］。

相比较于普通齿轮传动，行星齿轮传动结构复杂，制造与装配过程困难［2］。而行星轮系作为传动系统中主要承载与传递动力的系统，在运转过程中常会发生运动不平稳、噪音大的问题，严重影响了整个传动系统的可靠性与使用寿命［3］。现阶段研究者对行星齿轮传动的研究多以简单的单级传动为主［4-7］。较之单级行星齿轮传动，多级行星齿轮传动的运动学及动力学表现更为复杂［8-9］。采用虚拟样机技术对多级行星齿轮传动系统进行研究，在设计时，可对整个系统优化设计；在使用阶段也可对产生的问题找出问题的根源，设法优化改进。本文以二级行星齿轮传动系统为研究对象，结合三维造型设计软件PRO/E和机械系统动力学分析软件ADAMS，对传动系统进行运动学与动力学仿真分析，研究传动过程中各级输入输出轴的速度、齿轮之间的圆周力及径向力，研究结果可为多级行星齿轮减速器的优化设计和工程分析提供依据。

1 工作原理

以二级传动的2K-H（NWG）型行星传动为例，如图1：内齿轮Z3固定，在高速级传动过程中，太阳轮Z1与输入轴转速相同，行星轮Z2在自转的同时围绕Z1轴线公转，行星架H1围绕自身轴线转动；在低速级传动过程中，太阳轮Z4转速与行星架H1相同，行星轮Z5在自转的同时围绕Z4轴线公转，行星架H1绕自身轴线转动，其转速作为输出轴的输出转速。

图1 2K-H（NWG）型行星轮系

2 三维模型的建立

表1 二级行星齿轮减速器各级齿轮参数

2.1 圆柱齿轮的参数化建模

在PRO/E中，形状相同或相近的零部件以及系列化产品，可以用一组参数来表征其结构尺寸和属性，通过修改零部件的各种参数，得到不同规格的零部件，以实现零部件参数化设计［10］。对于二级行星齿轮减速器来说，需要数量较多的齿轮，通过对齿轮的参数化建模，只要输入或修改齿轮的一些基本参数（如齿数、模数、压力角以及齿宽等），软件系统便可自动生成某种类型齿轮的三维几何模型，或重建几何模型，提高了设计效率。

齿轮的参数化建立过程：①齿轮参数与关系式的输入：在PRO/E界面主菜单上单击“工具”“参数”，系统会弹出“参数”对话框。在该对话框中单击“添加”按钮，依次输入建立齿轮模型所需要的参数名称、值和说明。在主菜单上单击“工具”“关系”，在“关系”对话框中输入齿轮的分度圆直径关系、基圆直径关系、齿根圆直径关系和齿顶圆直径关系。②齿轮基本圆的创建；③渐开线的创建；④拉伸实体；⑤阵列轮齿；⑥其它特征的创建。

2.2 二级行星齿轮减速器传动系统装配

利用PRO/E建立二级行星齿轮减速器传动部分所有零件的三维模型图，然后对各个组件进行标准装配。将装配好的模型另存为Parasolid的文件。为方便观察齿轮传动内部结构，在装配体重隐藏内齿轮Z3，如图2。

图2 轮系传动部分内部图（不含内齿轮）

3 二级行星齿轮减速器的运动学分析

3.1 定义运动副

齿轮传动模型在导入ADAMS中时，无法保证所有齿轮的圆点在坐标轴上，这时有些齿轮的圆心坐标值不是一个整数。这种情况下，在做运动学分析时，齿轮副无法精确施加。对于ADAMS初学者来说，此时可以根据两传动齿轮的尺寸简化其传动，在ADAMS中建立以齿轮的分度圆直径为直径、齿轮厚度为高度的圆柱模型代替齿轮，行星齿轮传动中的行星齿轮确定其中一个的位置即可。高速级部分创建约束过程如下：利用ADAMS的JOINT功能模块对各部件施加运动约束。内齿轮Z3是与箱体固定在一起的，将其用固定副与大地（Ground）固定在一起。行星架与大地之间，行星架与行星轮之间，行星轮与太阳轮之间以及行星架H1与太阳轮Z1之间皆为旋转副。在太阳轮与行星轮、行星轮与内齿轮之间施加齿轮副。在定义齿轮副时，与行星轮相关的齿轮副的公共速度点定义在行星架H1上。

图3 简化后的高速级虚拟样机模型

3.2 定义运动

给行星齿轮传动系统加载MOTION，即给太阳轮Z1添加转速9000，设置仿真时间1s，步长100，对行星轮架H2进行运动学分析。使用Plotting查看行星架输出转速，即输出轴转速，行星架转速395.7。计算仿真结果得到传动比，而通过周转轮系传动比公式计算所得该系统传动比为，两数值大小基本吻合。由此可得通过PROE建立的行星齿轮传动系统的模型是正确的。

图4 低速级输出轴转速

4 行星轮系的动力学仿真

4.1 模型导入及添加约束

将模型导入ADAMS的View模块中，定义重力方向、将各个零件定义为刚体并重命名，定义各部件的质量、转动惯量等属性。利用ADAMS的JOINT功能模块对各部件施加运动约束。内齿轮用固定副与大地（Ground）固定在一起，各级行星架与大地之间，行星架与行星轮之间，行星轮与太阳轮之间以及行星架与太阳轮之间皆为旋转副。在太阳轮与行星轮、行星轮与内齿轮之间施加齿轮副。在定义齿轮副时，与行星轮相关的齿轮副的公共速度点定义在行星架上。

4.2 碰撞过程中碰撞参数的选取

在ADAMS的运动仿真过程中，为使齿轮间啮合力与实际效果更为接近，需要对齿轮件以及齿轮与行星架间定义碰撞参数。碰撞过程可以认为是一个变结构的动力学问题，对接触碰撞过程的描述目前主要有两种：经典碰撞模型和接触变形模型。经典碰撞模型不能给出碰撞时间，无法计算碰撞时的冲击力。在ADAMS中计算接触力的方法是基于接触碰撞模型的冲击函数法，它通过计入碰撞体接触表面的弹性和阻尼，建立碰撞过程中力和接触变性之间的本构关系，从而获得碰撞力的大小。

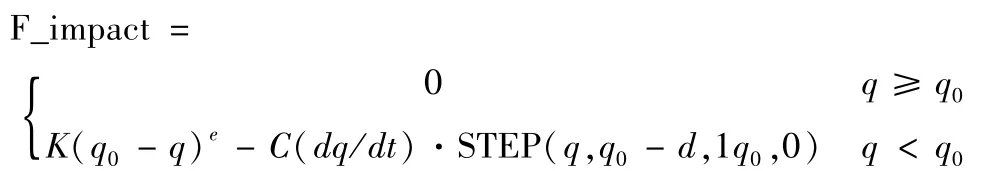
上式中，为阶跃函数，为两物体间的初始距离，q为两物体间的实际距离，两物体碰撞过程中所发生的变形量。当时，两物体不发生碰撞，其碰撞力为零；时，两物体发生碰撞，此时碰撞力的大小与Hertz接触刚度K、物体间的变形量、刚性系数e、阻尼系数C以及阻尼完全作用时变形量d有关。接触刚度K的大小取决于两个碰撞物体的材料与结构形状

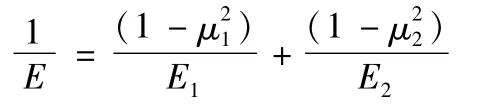
μ1、μ2为两接触材料的泊松比，E1、E2为接触材料的弹性模量［11］。

以高速级太阳轮与行星轮碰撞为例，设定两齿轮材料为45钢，泊松比μ1=μ2=0.27，弹性模量E1= E2=2.07e+11Pa。接触半径取两齿轮的分度圆半径［12］，R1=81mm，R2=123mm。经计算可得两齿轮的碰撞刚度系数K=10.4e+5N/mm。取刚性系数e= 1.5，阻尼系数C=50N·S-1/mm，变形量d=0.15mm，考虑到碰撞时两齿轮间的摩擦，按润滑处理，动摩擦系数取0.05，静摩擦系数取0.08。选取上述参数后即可进行行星齿轮传动系统的动力学仿真。

4.3 齿轮副受力分析

在高速级太阳轮分别加载扭矩SFORCE_1= 3000N·mm，6000N·mm，10000N·mm，15000N·mm。为更好观察太阳轮与行星轮之间圆周力与径向力的变化，将仿真时间设定为1.0s。图5a，5b两图分别为在太阳轮加载扭矩SFORCE_1=3000N·mm的情况下，太阳轮与行星齿轮沿ADAMS坐标系统x方向（圆周力方向）和y方向（径向力方向）的啮合力随时间变化曲线。由仿真图可观察，在启动阶段0s到0.2s有一个非稳定的上升阶段，这是在此阶段时间内对传动系统加载形成的。该阶段结束后，轮齿间相互作用的圆周力与径向力呈现稳定变化状态。啮合力稳定周期变化状态类似于正弦函数变化，这是齿轮周期性啮合、分离冲击造成的结果。切向力与径向力幅值基本相当、频谱特性相同，两者却存在于大约的相位差。图6，图7，图8分别是在太阳轮在加载扭矩6000N·mm，10000 N·mm，15000N·mm时，太阳轮与行星齿轮之间啮合力的变化曲线。

啮合力变化曲线分析：当输入扭矩小于 6000 N·mm时，传动系统运行平稳，齿轮间啮合力波动较小。随着输入端扭矩的增大，齿轮受尺寸、材料的约束，会发生弹性变形。随着齿轮的转动，弹性力不断积累而又不断释放。在此过程中，弹性力的增大在一定程度影响了啮合力变化。当输入扭矩大于10000N·mm时，齿轮间啮合力出现无规律的波动，齿轮由弹性变形变为塑性变形，当输入扭矩为15000N·mm可判断齿轮已基本失效，传动系统发生故障。

图5 扭矩为3000N·mm时变化曲线

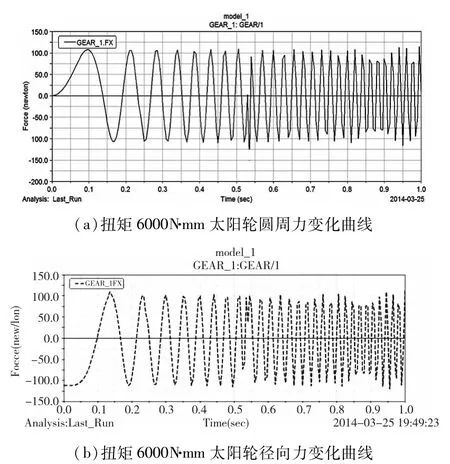
图6 扭矩为6000N·mm时变化曲线

图7 扭矩为10000N·mm时变化曲线

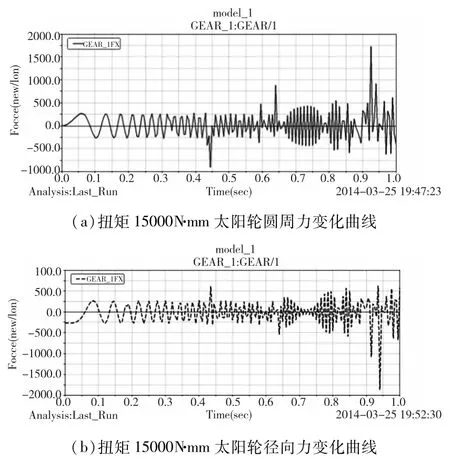
图8 扭矩为15000N·mm时变化曲线

5 结论

基于三维造型软件PRO/E，研究了渐开线齿轮及参数化齿轮的构建方法。将模型导入动力学仿真软件ADAMS中，施加各种运动副约束和碰撞，利用STEP函数施加太阳轮转速和负载，建立二级行星齿轮传动系统的虚拟样机模型。首先实现了行星齿轮传动系统的运动学仿真，得到输出轴的转速，输出结果与理论计算值相比较相差不大，基本符合设计要求。然后运用ADAMS动力学仿真功能对高速级太阳轮与行星轮之间的碰撞力进行分析，得到轮齿间在输入不同扭矩的条件下的圆周力与径向力变化曲线图。通过对啮合力变化曲线的分析，可判断输入扭矩在一定的范围时，行星齿轮传动系统可平稳运行，当输入扭矩增大到一定值时，齿轮间啮合力出现较大范围的波动，影响了系统的正常运行。当输入扭矩增大到一定值甚至会出现齿轮失效的情况。该结果可为行星齿轮减速器在实际运行中规避输入危险扭矩提供理论依据。基于虚拟样机技术的建模和仿真可以为多级行星齿轮传动系统的运动规律和动力学特性研究以及进一步的优化设计和工程分析提供理论依据。

［1］成大先.机械设计手册［M］.北京：化学工业出版社，2010.

［2］华顺刚，余国权，苏铁明.基于ADAMS的减速器虚拟样机建模及动力学仿真［J］.机械设计与研究，2006，22（6）：47-52.

［3］雷亚国，何正嘉，林京，等.行星齿轮箱故障诊断技术的研究进展［J］.机械工程学报，2011，47（19）：59-67.

［4］余震，沈琛林，陈雪辉.基于ADAMS的行星减速器运动学仿真研究［J］.安徽建筑工业学院学报，2009，17（5）：82-85.

［5］郭会珍，谭长均，陈俊锋.基于ADAMS的行星轮系动力学仿真［J］.机械传动，2013，37（5）：86-90.

［6］江志祥，朱增宝，季军.基于UG与ADAMS的行星齿轮减速器动力学仿真分析［J］.煤矿机械，2013（6）：43-44.

［7］余波，王家序，黄春美.基于ADAMS的孔销式少齿差行星减速器的设计与仿真分析［J］.机械设计与研究，2013，29（3）：23-27.

［8］杨建明，张策，林忠钦，等.行星齿轮传动动力学特性研究进展［J］.航空动力学报，2003，18（2）：299-304.

［9］孙涛，沈允文.行星齿轮传动非线性动力学方程求解与动态特性分析［J］.机械工程学报，2002，38（3）：11-15.

［10］冯玮，周启来.齿轮参数化设计系统的研究与实现［J］.制造业自动化，2011，33（4）：103-105.

［11］李增刚.ADAMS入门详解与实例［M］.北京：国防工业出版社，2010.

［12］龙凯，程颖.齿轮啮合力仿真计算的参数选取研究［J］.计算机仿真，2002，19（6）：87-91.

（编辑 李秀敏）

Dynamics Research of Two-stage Planetary Gear Transmission Based on PRO/E and ADAM S

ZHANG Xue-jun，GUO Jun-chao
（School of Mechanical Engineering of Northeast DianLi University，Jilin Jilin 132012，China）

Multi-stage planetary gear hascomplex structure.Its kinematics and dynamicsperformanceis difficult todetermine.In this paper，two-stage planetarygear transmissionfor the study，to determine the correctparametersbetween thesun gearmeshingplanetarygearwheel andtheuse of3D modeling softwarePRO/Ecreate a physicalmodel ofthe planetarygear system，adynamic analysis softwareADAMSplatformcreate a virtualprototypemodel for thetransmissionof thekinematics and dynamicssimulation.Radial forceobtained by simulationsystemsandperipheral forcetransmission ratio，the output speed of the output shaftand the gearbetweentheresultsanda highdegree of matchingresults，build a reasonableexplanationvirtualhoodmodel.The simulation resultscan provide the basisfor themulti-stage planetary gear reduceroptimal designandengineering analysis.

two-stage planetary gear；virtual prototyping；collision；dynamic simulation

TH132.41；TG506

A

1001-2265（2015）03-0093-04 DOI：10.13462/j.cnki.mmtamt.2015.03.025

2014-06-16；

2014-07-19

东北电力大学研究生创新基金项目（20130048）

张学军（1964—），男，吉林省吉林市人，东北电力大学教授，博士，研究方向为机械设计及理论、虚拟设计，（E-mail）zhangxuejun1964@ 163.com。