永磁直线电机二阶非奇异快速终端滑模控制*

孙宜标，陈展琴，王丽梅

（沈阳工业大学电气工程学院，沈阳 110870）

永磁直线电机二阶非奇异快速终端滑模控制*

孙宜标，陈展琴，王丽梅

（沈阳工业大学电气工程学院，沈阳 110870）

针对永磁直线电机伺服系统易受参数变化和负载扰动、端部效应等不确定因素影响的问题，提出一种二阶非奇异快速终端滑模控制方法来设计永磁直线电机位移控制器。该算法设计上避免了终端滑模的奇异区并且提高了其收敛速度，从而解决原有终端滑模的奇异性和速度收敛缓慢的问题。利用二阶滑模超螺旋控制律将不连续的控制作用在变量的高阶微分上，以削弱系统抖振现象。仿真结果表明，该策略不仅使系统具有较好的定位能力和很强的鲁棒性，同时还有效地削弱了系统的抖振现象。

非奇异终端滑模控制；二阶滑模；永磁直线电机；超螺旋算法

0 引言

为了满足伺服系统的高速度和高精度、定位的要求，直线电机作为直接驱动的主要部件在伺服系统中得到广泛的应用。直线电机消除了伺服系统中间机械传动机构所带来的不良影响，在高精度、高速响应、微进给伺服系统中具有非常大的优势。由于直线电机直接驱动负载，负载的变化和外部扰动将毫无衰减地直接作用在直线电机的动子上，使系统对负载扰动和参数变化都很敏感，所以要求系统具有较强的抗干扰能力和鲁棒性。为了提高伺服系统的抗干扰性和鲁棒性，如今一些现代控制理论被应用到直线电机的控制系统中，如：文献［1］采用鲁棒控制理论设计控制器，可使系统具有很好的鲁棒性，但控制器的设计过于保守；文献［2］采用自适应控制理论设计控制器，可以有效克服参数变化对系统的影响，但在参数变化较快、外部干扰频率高的情况下则效果不佳。文献［7］采用滑模变结构控制理论设计控制器，滑模变结构控制作为一种非线性不连续控制方法，因其算法简单，抗干扰能力强，易于工程实现等优点而受到广泛的关注。其存在的主要缺点就是抖振问题［6］。滑模面设计直接影响到系统状态收敛特性，是滑模变结构的基础。目前已有的滑模面主要有线性滑模面、终端滑模面、快速终端滑模面和非奇异终端滑模面等［3-6］。线性滑模使系统状态与期望轨迹之间偏差以指数形式渐进收敛，但系统状态永远无法到达期望轨迹［7］。而终端滑模在传统滑模中引入了非线性项，使系统收敛性有所改变，系统可在有限时间内收敛并达到期望轨迹［8-9］。但终端滑模控制存在奇异性问题，因此非奇异终端滑模控制方法被提出，从设计上避免了奇异区域并且保留了终端滑模在有限时间收敛的特性［10］。

本文采用二阶非奇异快速终端滑模的控制方法来设计永磁直线电机的位移控制器，综合的解决终端滑模控制的奇异、抖振和收敛缓慢的问题。将二阶滑模和非奇异终端滑模相结合既可削弱抖振也可解决终端滑模的奇异性问题，同时提高系统的收敛速度。进而提高系统的控制性能，使系统对于参数的不确定性，负载扰动扰等问题具有更强的鲁棒性。

1 永磁直线电机的数学模型

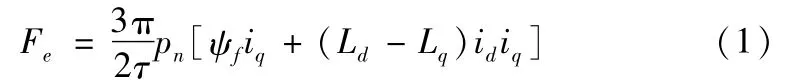
式中，pn为极对数；τ为极距；ψf为永磁体磁链；Ld为直轴励磁电感；Lq为交轴励磁电感；id为直轴电流；iq为交轴电流。当只考虑基波分量时，电流内环采用id=0的控制策略，则电磁推力为：

永磁直线电机电磁推力表达式为：

PMLSM的机械运动方程为：

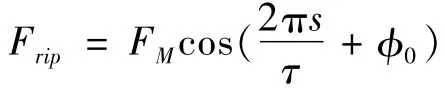
FM—端部效应推力波动幅值；τ—极距；φ0—初始相位电角度；Ffric为摩擦力；Ffric=［fc+（fsfc）e-（v/vs）2］sgn（v）；fc—库伦摩擦系数；fs—静态摩擦系数；v—动子速度；vs—临界摩擦速度。

2 永磁直线电机二阶非奇异快速终端滑模控制

2.1 滑模变量的设计

为了便于描述，令x=［x1，x2］T=［s，v］T为系统的状态变量，输入控制量为u=iq，则系统（3）的状态方程形式为：

定义系统的二阶非奇异快速终端滑模变量为：

其中，0＜α＜1，β∈R+，p，q∈N为奇数，λ＞p/q，要求1＜p/q＜2来满足滑模面的非奇异性。

由该滑模面可知，当系统状态靠近平衡点时，可忽略跟踪误差e（t）的高次项，其收敛速度近似于非奇异终端滑模；当系统状态远离平衡点时，跟踪误差e（t）的高次项起主要作用，所以其收敛速度比非奇异终端滑模更快。

根据滑模控制系统设计的要求必须满足滑模变量σ及其一阶导数 .σ收敛到零点。

滑模变量的一阶导数.σ为

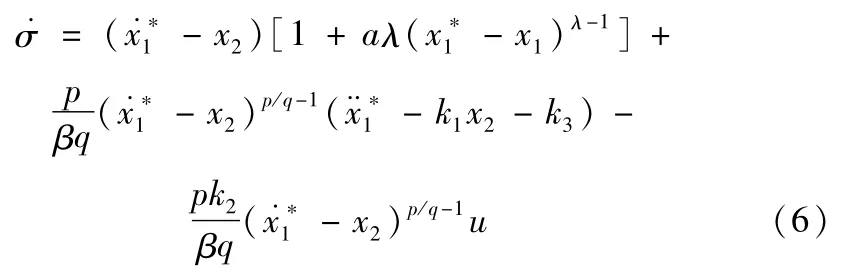
2.2 超螺旋控制律的设计

假设式（5）中所设计的滑模变量σ为不确定系统的输出变量，且由式（6）可知二阶滑模控制系统的相对阶为1，需选择适当的u使输出变量σ及其导数在有限时间内收敛为零。

式（6）滑模变量的状态方程可写为：

其中，φ（t，x1，x2），r（t，x1，x2）是不确定函数，且满足以下边界条件：

采用超螺旋算法可设状态轨迹在σ-.σ平面上有限时间内围绕原点螺旋式收敛到原点。具体算法如下：

其中，M1、M2满足：

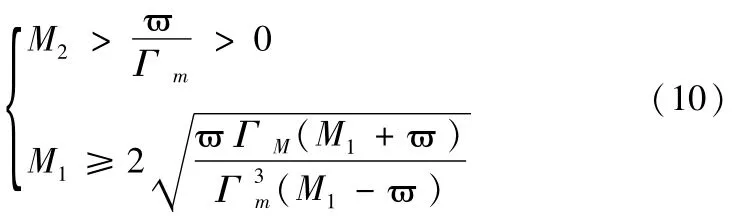
定理：对于系统（4），选取非线性滑模变量（5），满足条件（8），在超螺旋控制律（9）作用下，若满足条件（10），则系统将在有限时间内收敛。

证：选取李雅普诺夫函数为V（t）=0.5σ2（t），则对V（t）求导得：

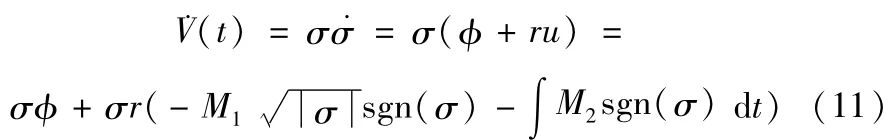
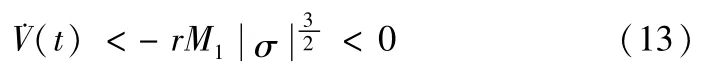
由李雅普诺夫稳定性理论可知，当满足滑模到达条件.V（t）=σ＜0时，滑模面σ及其导数可在有限时间内收敛到零。

3 仿真结果及分析

采用MATLAB7.10进行仿真研究，永磁直线电机的参数如下：额定推力Fe=502N，推力系数kf= 50.7N/A，动子电阻Rs=2.1Ω，动子dq轴电感L= 41.4mH，永磁体磁链ψf=0.09Wb，极距τ=16mm，极对数pn=6，动子质量M=12kg，粘滞摩擦因数Bv= 8Ns/m，端部效应等效阻力Frip=40cos（392s），摩擦力Ffric=［10+5e-（v/4）2］sgn（v）。

为了验证本文所提出控制策略的有效性，将超螺旋控制方法的二阶非奇异快速终端滑模控制（方法一）和等速趋近律控制方法的终端滑模控制（方法二）、螺旋控制方法的二阶非奇异终端滑模控制（方法三）进行比较。

方法二的滑模变量和控制律为：

其中，η，β1∈R+，0＜q1/p1＜1，p1，q1∈N为奇数。

方法三的滑模变量和控制律为：

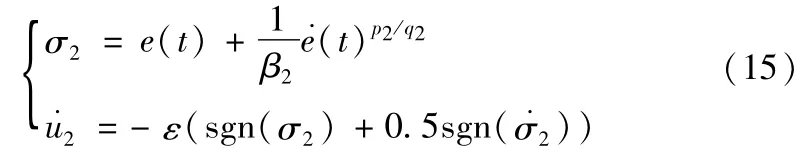
其中，β2∈R+，ε＜0，1＜p2/q2＜2，p2，q2∈N为奇数。

方法一参数为：α=0.03，λ=2.1，β=120，p =7，q=5，M1=600，M2=300；方法二参数为：β1=47.62，q1=3，p3=5，η=400。方法三参数为：β2=62.5，p2=11，q2=7，ε=800。

为了验证控制策略的有效性，永磁直线电机空载启动，阶跃参考信号s=0.3m，在0.5s时突加FL= 500N的阶跃负载阻力，并且在永磁直线电机启动后将动子质量M变为原来的3倍，根据条件（8）和（10）调节控制器的参数直到系统达到最佳状态。

图2为控制方法一（曲线B）、方法二（曲线C）、方法三（曲线A）时参数变化前的位移响应曲线，图2为参数变化后的位移阶跃响应曲线。

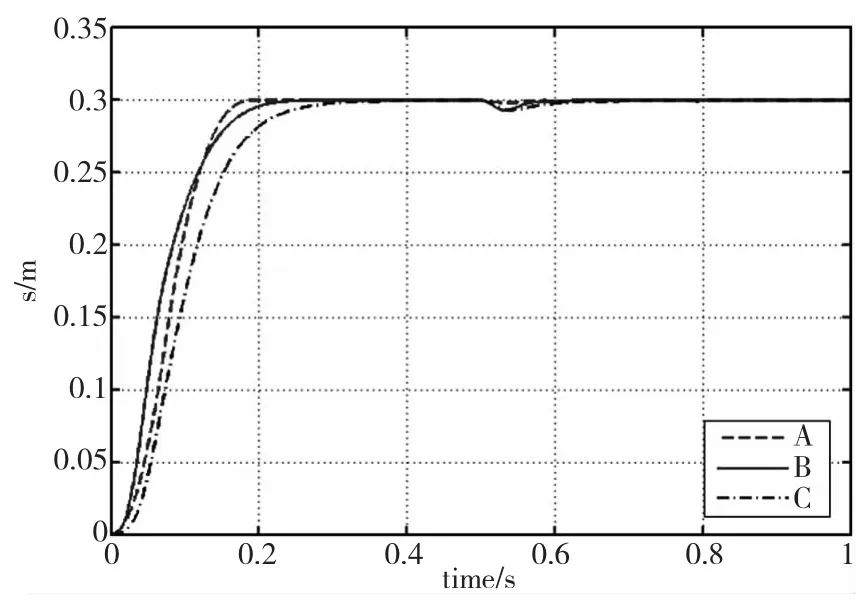
图1 参数变化前位移响应曲线

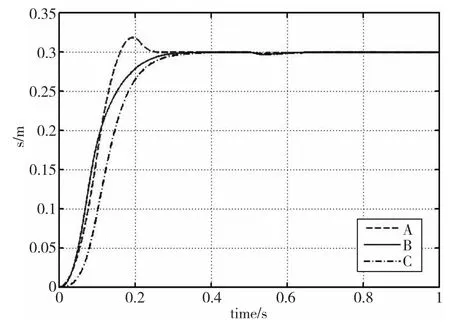
图2 参数变化后位移响应曲线

由上图1、2可知，本文所设计的二阶非奇异快速终端滑模控制策略与其它两种控制策略相比，使系统具有良好的位置定位能力，对负载的干扰和系统参数变化的鲁棒性更强。系统受到外部扰动后能在更短的时间内恢复稳定，满足了直接进给伺服系统对抗干扰能力的要求。

图3为参数变化前超螺旋控制律的二阶非奇异快速终端滑模控制系统电流iq曲线，图4为参数变化前等速趋近律控制终端滑模控制系统的电流iq曲线，图5为参数变化前螺旋控制律非奇异二阶滑模控制系统电流iq曲线。通过对比可以看出，超螺旋算法控制的二阶非奇异终端滑模可以明显的削弱系统抖振现象。

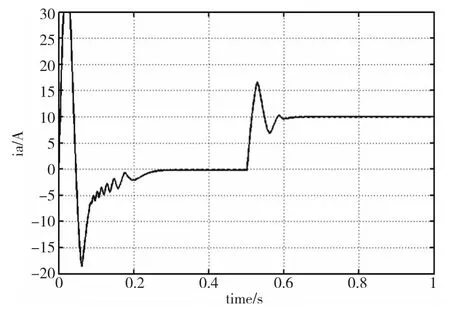
图3 超螺旋控制律二阶非奇异快速终端滑模控制的电流iq曲线

图4 等速趋近律控制的终端滑模控制电流iq曲线

图5 螺旋控制律控制的二阶非奇异终端滑模控制电流iq曲线

图6 为参数未变化之前且无负载的超螺旋控制律二阶非奇异快速终端滑模控制器的滑模变量的相平面轨迹，图7为参数变化之后加负载时相平面轨迹。可以看出系统具有较好的抗干扰能力和鲁棒性。

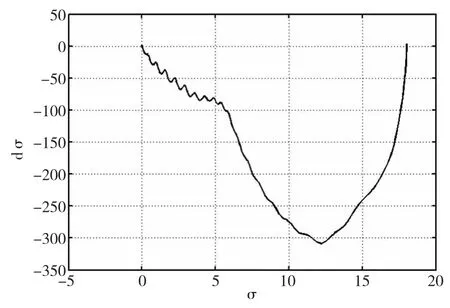
图6 参数未变化之前的无负载滑模变量相平面轨迹

图7 参数变化之后加负载时相平面轨迹

4 结束语

本文将二阶滑模控制和非奇异快速终端滑模控制相结合，设计二阶非奇异快速终端滑模控制器。该方法使滑模变量及其导数在有限时间内收敛到零，并有效的解决了终端滑模奇异性的问题，同时解决了在距离平衡点较远时系统收敛速度缓慢的问题，提高了收敛速度。二阶滑模的设计使不连续的控制作用在变量的高阶微分上，削弱了系统的抖振。仿真结果表明，本文所设计的二阶非奇异快速终端滑模控制器不仅保证了永磁直线电机伺服系统的定位能力和鲁棒性，还削弱了系统的抖振。

［1］李义强，周惠兴，王先逵，等.直线电机伺服定位系统时间最优鲁棒控制［J］.电机与控制学报，2011，15（3）：13-18.

［2］陈渊睿，吴捷，N.C.Cheung.永磁直线电机的模型参考自适应控制［J］.华南理工大学学报：自然科学版，2003，31（6）：31-35.

［3］Jo YH，Lee YH，and Park KB.Design of Extended Terminal Sliding Mode Control Systems［J］.Journal of Institute of Control Robotics and Systems，2011，17（3）：236-240.

［4］庄开宇，张克勤，苏宏业，等.高阶非线性系统的Terminal滑模控制［J］.浙江大学学报：工学版，2002，36（5）：482-486.

［5］康宇，奚宏生，季海波.不确定多变量线性系统的快速收敛滑模变结构控制［J］.中国科学技术大学学报，2003，33（6）：718-725.

［6］冯勇，鲍晟，余星火.非奇异终端滑模控制系统的设计方法［J］.控制与决策，2002，2（17）：195-198.

［7］Sunan N.Huang，Kok Kiong Tan，and Tong Heng Lee. Sliding-Mode Monitoring and Control of Linear Drives［J］. IEEE Transactions on Industrial Electronics，2012，56（9）：3532-3540.

［8］Levant，Arie.Quasi-continuous high-order sliding mode controllers［J］.IEEE Transactions on Automatic Control，2005，50（11）：1812-1816.

［9］Yong Feng，Xinghuo Yu，Zhihong Man.Non-singular adaptive terminal sliding mode control of rigid manipulators［J］. Automatica，2008，38（12）：2159-216.

［10］刘金琨.滑模变结构控制MATLAB仿真［J］北京：清华大学出版社，2005.

（编辑 李秀敏）

Second-Order Nonsingular Fast Terminal Sliding Mode Displacement Control for PMLM

SUN Yi-biao，CHEN Zhan-qin，WANG Li-mei
（Electric Engineering School，Shenyang University of Technology，Shenyang 110870，China）

Because of the permanent magnet linear motor servo system is vulnerable to be influenced by many uncertain factors，such as the parameter variations and load disturbance，put forward a kind of higherorder nonsingular fast terminal sliding mode control method to design the displacement control of the permanent magnet linear motor.The algorithm is designed to avoid the singular area of terminal sliding mode and improve the convergence speed，so as to solve the singularity of the terminal sliding mode and speed problem of slow convergence.Using super twisting law of second-order sliding mode control put the discontinuous control on the higher order differential variables，in order to weaken the chattering of the system.Simulation results show that the strategy not only make the system has better capability of position and strong robustness，but also weaken the chattering of the system effectively.

nonsingular terminal sliding mode control；second-order sliding mode；permanent magnet linear motor；super twisting algorithm

TH165；TG659

A

1001-2265（2015）03-0086-04 DOI：10.13462/j.cnki.mmtamt.2015.03.023

2014-05-15

国家自然科学基金资助项目（51175349）；辽宁省高等学校优秀人才支持计划资助（LR2013006）；沈阳市科技计划项目（F13-316-1-48）

孙宜标（1970—），男，安徽巢湖人，沈阳工业大学副教授，博士，研究方向为交流伺服系统、鲁棒控制、非线性系统等，（E-mail）sunyibiao2004@126.com。