三自由度可调并联机构的位置与运动学分析*

姚 翔，林光春，豆依玲

（四川大学制造科学与工程学院，成都 610065）

三自由度可调并联机构的位置与运动学分析*

姚 翔，林光春，豆依玲

（四川大学制造科学与工程学院，成都 610065）

针对一种三自由度的球面并联平台机构，基于符号-数字方法，建立了机构的位置正解数学模型，在此基础上推导出了末端执行器（动平台）球铰质心点的速度、加速度的正反解数学模型，研究了机构的运动学特性。利用Matlab符号运算对模型进行实例求解，验证了该方法的正确性。研究了调节驱动杆杆长和速度时动平台位置的变化规律，对该机构的动力学研究提供了基础。

三自由度；可调并联机构；位置分析

0 引言

可调机构比一般机构更具柔性，且可靠性高、精确度好、容易制造。球面并联机构具有结构紧凑、刚度大、承载能力强、位置误差不累积等特点。可调球面并联机构结合了可调机构和球面并联机构的优点，且具有较大的工作空间、能使输出构件完成多个任务要求，因此可广泛应用于机器人的腕关节、卫星定向装置、机械加工的回转工作台等。其中少自由度并联机构成为当前研究的热点，国内外在这一领域已经进行了大量的研究工作。三自由度并联机构可以满足大多数工业操作的需要，机构的复杂度和成本较低，运动学和动力学的模型较简单。故三自由度并联机构具有广阔的应用前景。球面三自由度并联机构具有刚度高、工作空间大等优点，如在并联机床上使用，可以实现大倾角加工，故对它的研究具有十分重要的意义。本文基于Matlab符号运算技术对机构进行位置分析与运动学分析，并研究了调节机构的几何参数对动平台位置的影响。

图1 机构简图

1 机构简介和坐标系建立

图1所示为三自由度球心可调并联机构简图。它由一个静平台（P1P2P3）和一个动平台（P＇1P＇2P＇3）通过三条驱动杆（l1l2l3）和一条调节杆（l4）组成，三条驱动杆的结构相同，呈正三角形对称分布，驱动杆分别用虎克铰和球铰与静平台和动平台联接，驱动杆上各有一个移动副。静平台形心（P0）与动平台形心（P＇0）用调节杆联接，该调节杆与静平台固联在一起，与动平台用球铰联接。建立静坐标系T1（P＇0XYZ）和动坐标系T2（P＇0xyz），如图1所示，动坐标系原点与静坐标系原点重合，位于动平台与静平台的几何中心，z轴为P＇0P＇1方向，x轴垂直于 z轴，并始终位于动平台P＇1P＇2P＇3平面内，y轴始终垂直于该平面。Z轴为P＇0P1方向，P＇0P1P0三点为不动点，X轴垂直于该三点组成的平面，Y轴可由右手定理得出。

2 位置分析

位置分析涉及位置的逆解和正解分析。位置正解是指给定始端输入量，求得末端输出量。根据T1和T2坐标系的建立，静平台三个铰点P1，P2，P3的坐标在T1中表示为：P1（x1，y1，z1），P2（x2，y2，z2），P3（x3，y3，z3）；动平台三个铰点P＇1，P＇2，P＇3的坐标在T2中表示为：P＇1（x＇1，y＇1，z＇1），P＇2（x＇2，y＇2，z＇2），P＇3（x＇3，y＇3，z＇3），且x1=y1=0；x＇1=y＇1=y＇2=y＇3=0。通过欧拉变换Z-Y-Z型，反映动平台最终姿态的矩阵为：R（φz，θy，ψz）=［Rzφ］［Ryθ］［Rzψ］=

设此并联机构的动平台和静平台的半径分别为r，R。因此在动坐标系T2中，动平台上球铰质心处的坐标为：P＇1=（0，0，r），P＇2=（-0.5×31/2r，0，-0.5 r），P＇3=（0.5×31/2r，0，-0.5r）。静平台上球铰质心处在静坐标系T1里的坐标为：P1=（0，0，z1），P2=（-0.5×31/2R，y2，z2），P3=（0.5×31/2R，y3，z3）。其中z1=（l42+R2）1/2，y2=y3=1.5Rl4/（l4

2+R2）1/2，z2=z3=（l4

2+R2）1/2-1.5R2/（l42+R2）1/2

将动平台球铰质心点的坐标表示在静坐标系T1上为：

式中i=1，2，3；φ、θ、ψ为欧拉角。

根据机构的几何特点，三条驱动杆的长度可以由Pi，Pi＇两点的坐标表示，建立方程：

式中i=1，2，3，将各点坐标代入式（3）得：

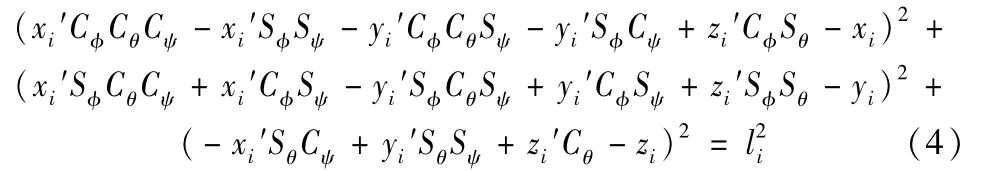
式中i=1，2，3，当i=1时，化简式（4）可得：θ=arccos［（z＇1）2+（z1）2-（l1）2］/2z1＇z1

当i=2，3时，可得：

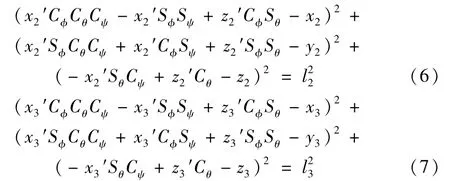
式（6）、（7）化简可得：

综上可知并联机构的位置解的数学模型。

运用万能公式化简式（8），则令：x=tan（φ/2），y=tan（ψ/2），可得如下表达式：sinφ=2x/（1+x2），cosφ=（1-x2）/（1+x2），sinψ=2y/（1+y2），cosψ=（1-y2）/（1+y2），代入（8）可得：

式中系数Ai，Bi（i=1～9）均由机构各个参数所确定，在此不表示。故根据以上求解方法，若有三根驱动杆和中间可调杆的杆长，通过Matlab编程求解式（9）两个方程，求得x，y的值，将其回代万能公式，可得出三个欧拉角度值，再通过式（2）得出动平台位置姿态。

3 运动学分析

3.1 速度分析

设动平台的位姿速度和加速度矢量分别为：

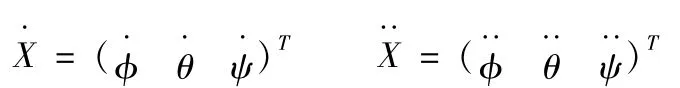
三个驱动杆li的速度矢量和加速度矢量分别为：

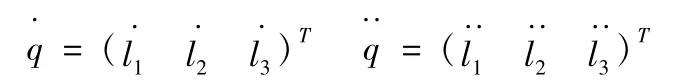
对于并联机构的末端执行器（动平台）的任意一个位姿，三根驱动杆有唯一的长度值与之对应。那么第i根驱动杆长度由式子计算：li=fi（X）=fi（x，y，z，φ，θ，ψ），其中x，y，z为动平台铰点在静坐标系中的坐标。等式两边分别对时间t求导得：

将式子写成矩阵形式，可得到速度逆解。数学模型：

考虑到与串并联机器人机构雅克比矩阵J的定义一致性，令G=J-1，上式两边左乘G-1，得出速度正解数学模型：

根据以上思路，式（8）两边分别对时间t求导得（i=1，2，3）：

3.2 加速度分析

等式li=fi（X）=fi（φ，θ，ψ）两边分别对时间求二阶导数，并整理得：

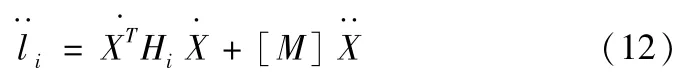
其中矩阵Hi的第1，第2和第3列元素分别为：

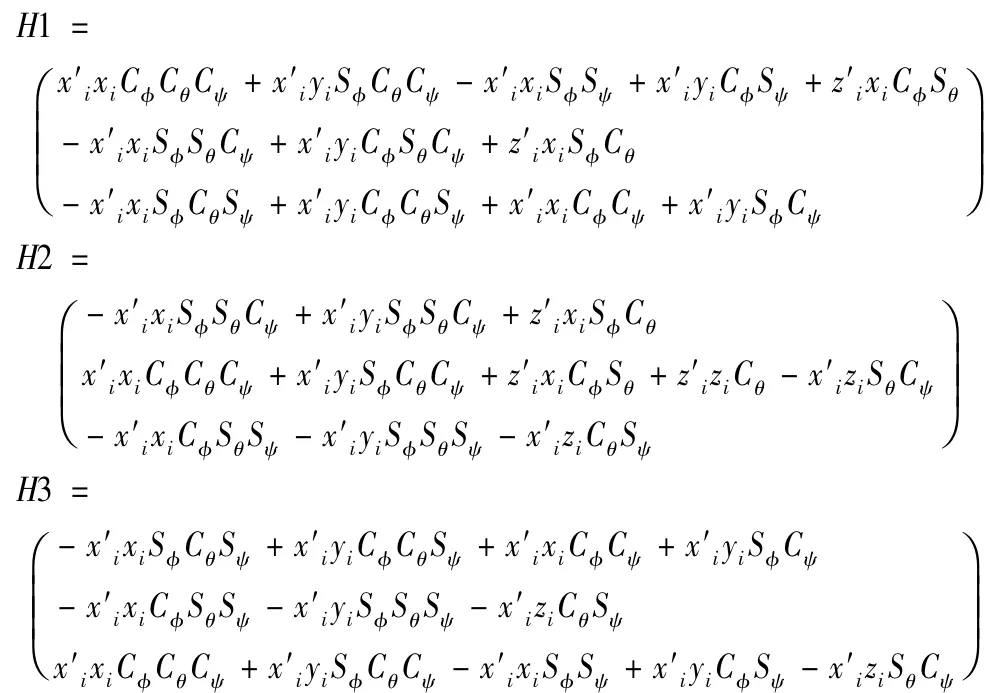
将式li=fi（X）=fi（φ，θ，ψ）写成矩阵形式，可得机构的加速度逆解模型：

其中H为加速度系数影响矩阵。上式两边同乘［M］-1，可得出加速度正解的数学模型：

4 机构的可调性

机构的可调性体现在，改变l4杆上开尾销联接（如图2所示）位置来调节杆长，从未达到改变球心位置，完成多个任务要求，从而满足实际应用中不同球心位置的要求。根据活动平台的不同位置和姿态要求，通过调节l4杆长和分别驱动三根支链的移动副，可快速可靠地执行动平台的输出操作。该机构的三维效果图如图3所示。

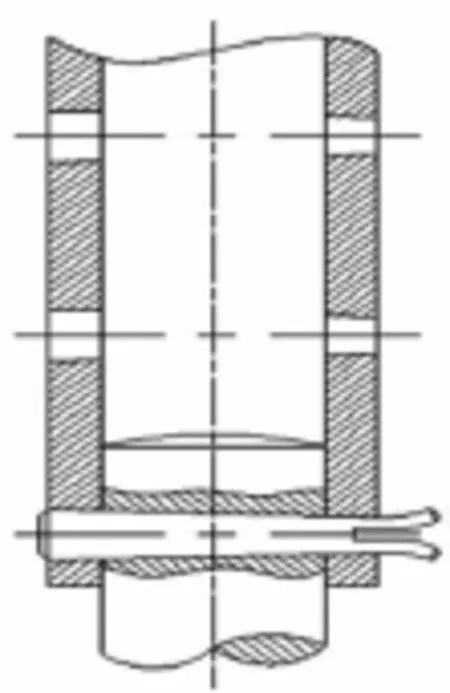
图2 l4杆可调节处的局部结构示意图

图3 并联机构的三维效果图

5 实例分析

系统参数：并联机构参数l1，l2，l3驱动杆取值范围在465mm至655mm之间变化，平均分布时，l1，l2，l3杆长为515mm。故取机构的两种姿态：①l1=550，l2= 500，l3=600，l4=500，r=170，R=280；②l4=480，其余参数不变。通过上述位置分析方法，上机运用Matlab编程求解式（9）得到x，y的实数解。姿态①、②分别各有两组实数解，如表1所示。将实数解回代，可得动平台位姿的欧拉角。如表2所示。再可换算出动平台球铰质心点在T1的坐标。

表1 x和y的实数解

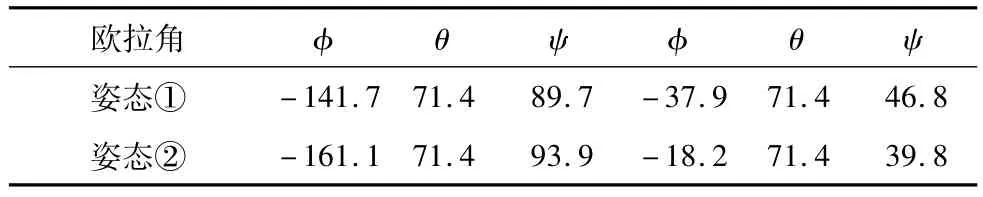
表2 欧拉角度值（°）

当三根驱动输入杆的杆长与时间的函数关系为l1=515+10t，l2=515-5t，，l3=515+5t时，根据上述速度、加速度解析模型，通过Matlab编程求解可得速度、加速度随时间的变化曲线，如图4，图5所示。

图4 动平台角速度

图5 动平台角加速度

5 结束语

本文提出了一种球心可调的移动副驱动的三自由度球面并联机构，该机构具有结构简单、控制简单等优点。基于符号或数字-符号法的球面并联机构分析与研究，将是球面机构研究的一个重要方向。采用Matlab符号运算方法，求解出了机构位置、速度、加速度在相应机构参数下的值，为该机构的进一步研究和应用提供了理论工具。研究了调节驱动杆杆长和速度时动平台位置的变化规律，研究结果对这类机构的动态性能评估与设计选型具有重要意义。

［1］田鑫，王帮峰，吴佳俊.基于3-RPS并联机构的自适应机翼方法实现［J］.科学技术与工程，2011，11（9）：1963-1967.

［2］刘善增，余跃庆，侣国宁，等.三自由度并联机器人的运动学和动力学分析［J］.机械工程学报，2009，45（8）：11-14.

［3］刘艳芳，杨随先.球面机构研究动向［J］.机械设计与研究，2010，26（1）：32-35.

［4］王进戈，张均富，王强，等.球面五杆机构的运动学与性能分析［J］.机械工程学报，2008，44（8）：33-38.

［5］杨加伦，高峰，史立峰.正交三自由度球面并联机构的位置正反解新方法［J］.机械设计与研究，2008，24（3）：30-36.

［6］刘善增，余跃庆，杨建新，等.三自由度并联机器人的运动学与动力学分析［J］.机械工程学报，2009，45（8）：12-17.

［7］HUANG Peng，WANG Jinsong，QIAN jie.Dimensional Synthesis for 3-PRS Mechanism Based on Identifiability Performance［J］.CHINESE JOURNAL OF MECHANICAL ENGINEERING，2012，25（2）：234-238.

［8］黄真，赵永生，赵铁石.高等空间机构学［M］.北京：高等教育出版社，2006.

［9］黄忠霖，黄京，徐礼锯，等.Matlab符号运算及其应用［M］.北京：国防工业出版社，2004.

［10］傅则绍，卢子馨.机构设计［M］.北京：石油大学出版社，1998.

（编辑 李秀敏）

Positional and Kinematics Analysis of Adjustable Three-DOF Parallel Mechanism

YAO Xiang，LIN Guang-chun，DOU Yi-ling
（College of Manufacturing Science and Engineering，Sichuan University，Chengdu 610065，China）

Solution of positional analysis is acquired concerning a spherical three-DOF adjustable parallel mechanism based on symbolic and digital method.On this basis，solutions＇mathematical model of velocity and acceleration of hinge points of the moving platform are obtained.Symbolic computation of software Matlabis used to solve mathematical model in a practical example，which verifies the correctness of the method. Then the variety of regularity of the moving platform position is researched when adjusting the length and velocity of the drive legs，it provides a basis for the dynamics of the mechanism.

three degree of freedom；adjustable parallel mechanism；positional analysis

TH112；TG659

A

1001-2265（2015）03-0059-03 DOI：10.13462/j.cnki.mmtamt.2015.03.016

2014-12-09；

2015-01-13

国家自然科学基金项目（50375104）

姚翔（1990—）男，四川龙泉人，四川大学硕士研究生，研究方向为机构与工业机器人，（E-mail）279146296@qq.com。