基于蒙特卡洛法的七自由度拟人机械臂工作空间分析*

何价来，罗金良，宦朋松，邓 健

（南华大学机械工程学院，湖南衡阳 421001）

基于蒙特卡洛法的七自由度拟人机械臂工作空间分析*

何价来，罗金良，宦朋松，邓 健

（南华大学机械工程学院，湖南衡阳 421001）

应用D-H法对七自由度拟人机械臂建立关节坐标系并确定杆系参数，建立机械臂运动学模型，应用齐次变换法推导出机械臂末端执行器的位姿。根据机械臂关节空间到工作空间的映射关系，提出采用蒙特卡洛法分析该机械臂的工作空间，得出机械臂工作空间的云图。为后续的机械人轨迹规划、动力学分析、运动控制和参数优化提供了参考依据。

蒙特卡洛法；七自由度；拟人机械臂

0 引言

机器人技术是综合了计算机、控制论、机构学、信息和传感技术、人工智能、仿生学等多种学科而形成的高技术，是当代研究十分活跃、应用日益广泛的领域。拟人机械臂这种独特的设备与其他机械臂相比，具有高度的适应性与灵活性［1］，具体表现在：对环境要求低、动作灵活、能量消耗小。作为机器人研究领域最活跃的研究方向之一，拟人机械臂是各国学者研究的热点，更是现代制造业自动化的最新发展趋势和方向［2-3］。

机械臂的灵活程度对其工作能力起着至关重要的作用。B.Roth在1975年提出了工作空间的概念，然后在机器人学界进行了一系列的讨论。机械臂的工作空间是衡量机械臂运动灵活程度的一个重要的运动学指标，它是指机械臂末端执行器坐标点所能到达的空间点集合。目前，机械臂工作空间的求解方法主要有图解法、解析法和数值法。图解法和解析法都受关节数目的限制，对于有些机械臂无法准确描述，数值法计算量太大，对于有些边界曲面可靠性得不到保证［4，9］。本文采用从数值法衍生发展出来的基于随机概率的算法：蒙特卡洛法［6］。随着计算机技术的飞速发展，蒙特卡洛法得到了越来越广泛的应用。

本文以七自由度拟人机械臂为研究对象，利用DH法对其进行运动学建模，推导出机械臂末端执行器的位姿，在MATLAB环境下采用蒙特卡洛法对拟人机械臂进行工作空间分析。

1 拟人机械臂结构及连杆参数

本文研究的七自由度拟人机械臂实物如图1所示。七自由度拟人机械臂由肩关节、肘关节和腕关节组成，其中：肩关节有三个自由度，肘关节有一个自由度，腕关节有三个自由度，机械臂的结构模型如图2所示。肩关节和肘关节用于确定机械臂的空间位置，腕关节用于确定机械臂的姿态［8］。

图1 七自由度拟人机械臂

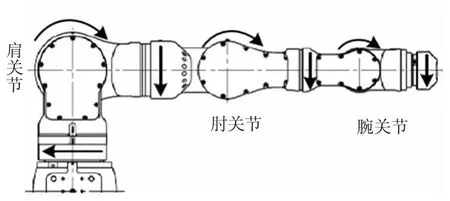
图2 七自由度拟人机械臂结构模型

在1955年，Denavit和Hartenberg在“ASME Journal of Applied Mechanics”上发表的论文［5］对机器人进行表示和建模，并推导出了机器人的运动学方程，这已经成为表示机器人和机器人运动学进行建模的标准方法。D-H模型描述了对机器人连杆和关节进行建模的一种非常简单的方法，可用于任何机器人构型，而与机器人的结构顺序和复杂程度无关。它可以用于表示已经讨论过的任何坐标中的变换，也可以用于表示全旋转的链式/拟人型机器人、SCARA机器人或任何可能的关节和连杆组合［10-12］。

为了描述机械臂相邻杆件之间的运动关系，对图2所示的机械臂结构模型采用D-H法对机器人运动学进行建模，建立机器人各关节的参考坐标系。机械臂连杆坐标系如图3所示，D-H参数如表1所示。其中，θi为关节变量：θimin为关节变量下限，θimax为关节变量上限；di，αi-1和ai-1为三个固定不变的连杆参数。

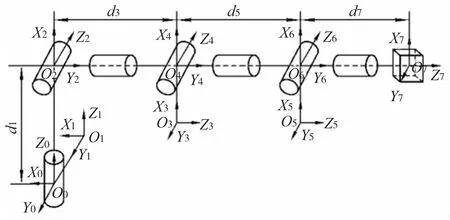
图3 七自由度拟人机械臂连杆坐标系

表1 七自由度拟人机械臂D-H参数表

2 正运动学分析

机器人的运动学分析是进行机器人技术研究的前提，是机器人工作空间分析和机器人运动控制的基础。机械臂的正运动学分析是：已知机械臂杆件几何参数和关节角矢量，求机械臂末端执行器相对于参考坐标系的位置和姿态。正运动学变换也就是由关节空间向直角空间的变换。

机器人相邻关节坐标系i-1和i之间的位姿变换矩阵为：

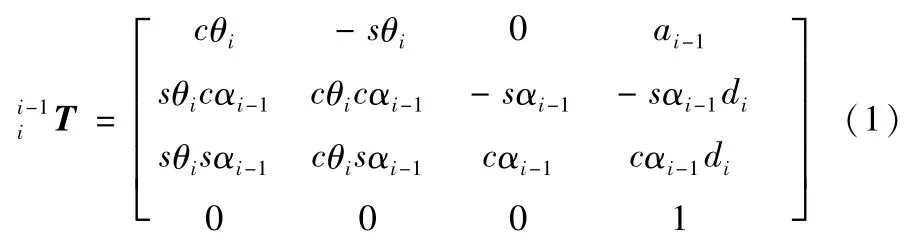
式中cθi=cos（θi），sθi=sin（θi），cαi-1=cos（αi-1），sαi-1=sin（αi-1）。利用表1的机械臂D-H参数和式（1），可以建立拟人机械臂相应各关节坐标系之间的位姿变换矩阵如下所示：

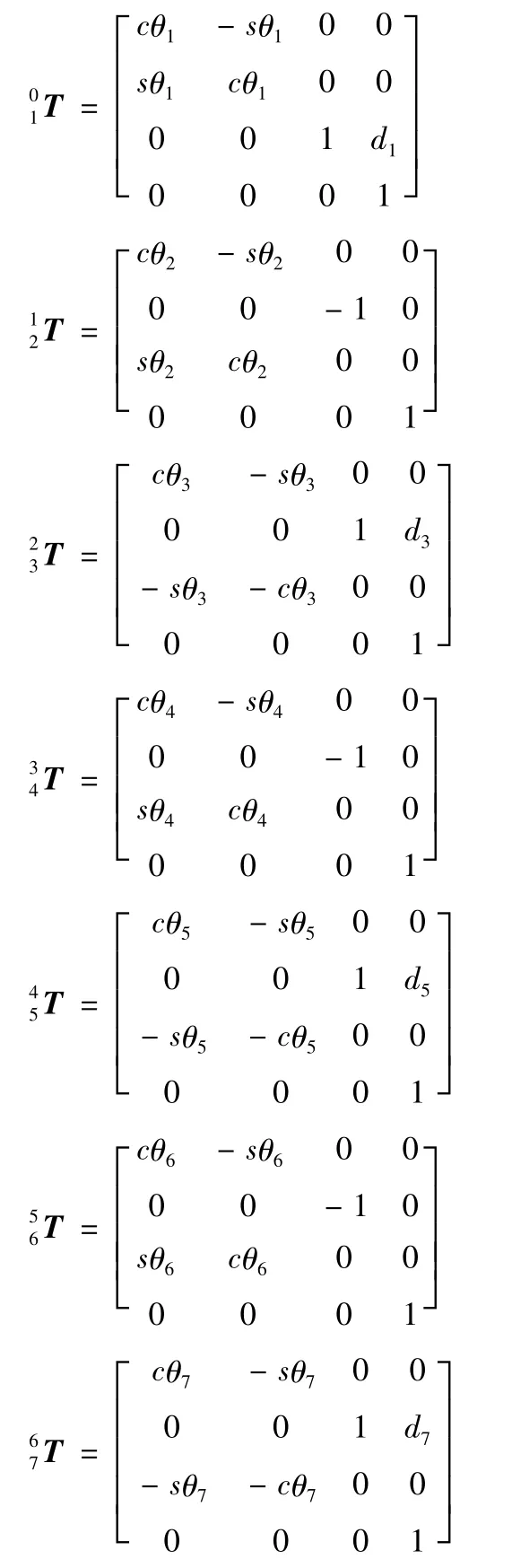
机械臂的末端坐标系O7相对于基坐标O0的位姿变换矩阵为：

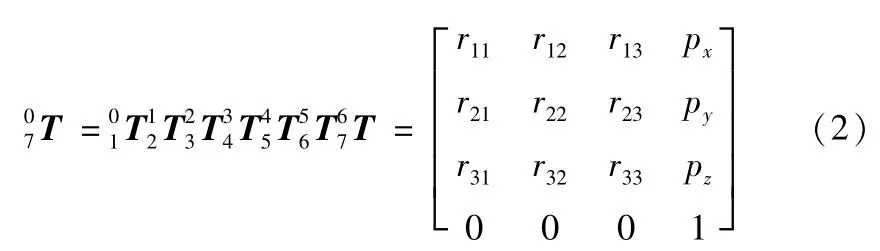
3 拟人机械臂工作空间分析

3.1 蒙特卡洛法机械臂工作空间分析

在机器人操作中，机构工作空间是末端执行件的工作区域描述，它是衡量机构性能的重要指标，在机构设计、控制和操作等方面具有重要意义。根据机器人的构型、连杆及腕关节的大小，机械人能到达的点的集合称为工作空间。工作空间用数学方法通过列写方程来确定，这些方程规定了机器人连杆与关节的约束条件。可达工作空间指末端执行件上某一参考点可以到达的所有点的集合，这种工作空间不考虑末端执行件的姿态。为确保机器人能到达要求的点，必须研究其工作空间［13-25］。

蒙特卡洛法（Monte Carlo method），又称统计模拟法，是借助于随机抽样（伪随机数）来解决数学问题的数值方法，在工程上被广泛应用于描述某些随机的物理现象。该方法易实现图形显示功能，计算速度快、简单，省却了繁复的数学推导和演算过程，适合于任何关节型机械臂工作空间的求解，对关节变量的变化范围没有限制，其误差也与维数无关。蒙特卡洛法应用于机械臂工作空间求解的基本思想是：机械臂的各关节是在其相应取值范围内工作的，当所有关节在相应取值范围内随机遍历取值后，末端点的所有随机值的集合就构成了机械臂的工作空间。在MATLAB中利用蒙特卡罗法求解机械臂工作空间的具体步骤如下：

（1）根据机械臂运动学正解，求出机械臂末端执行器相对于基座坐标系的位置向量 ［pxpypz］T，由于机械臂可达工作空间指末端执行件上某一参考点可以到达的所有点的集合，这种工作空间不考虑末端执行件的姿态，因此我们没有必要求出末端执行器的姿态向量。

（2）在各关节变量取值范围内，利用rand（j）函数产生N个0到1之间的随机值作为随机步长变量（j= 1，2，···，N），即（θimax-θimin）rand（j），从而得到机械臂关节变量的伪随机值为：

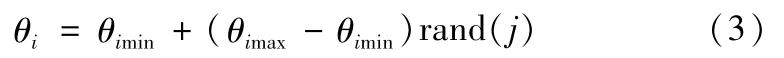
式中θimin为关节变量下限，θimax为关节变量上限；i为关节数目，取1～7。

（3）将步骤（2）中求得的N个关节变量的伪随机值代入运动学正解方程，求出机械臂末端点的相对应的位置向量。坐标点值数目越多，越能反映机械臂的实际工作空间。

（4）将所得机械臂末端点位置向量值按照比例，用描点方式显示在计算机图形设备中，就得到机械臂的工作空间点云图，也即机械臂的蒙特卡洛工作空间。

3.2 基于蒙特卡洛法的工作空间的生成

用蒙特卡洛法对机械臂的工作空间在MATLAB上进行仿真分析。取随机坐标点数目N=20000，得到七自由度拟人机械臂工作空间，如图4～7所示。

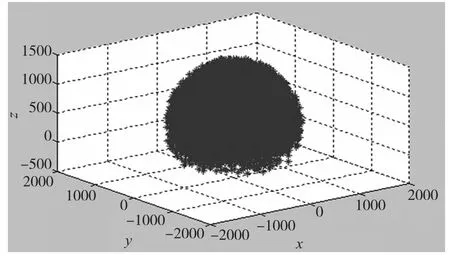
图4 机械臂可达工作空间三维图

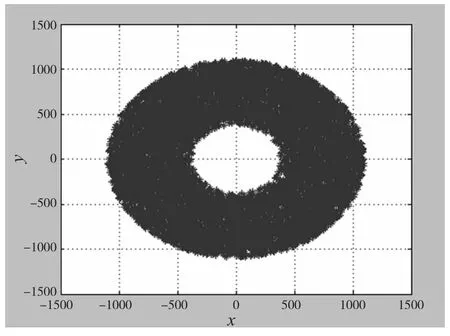
图5 xoy截面投影图

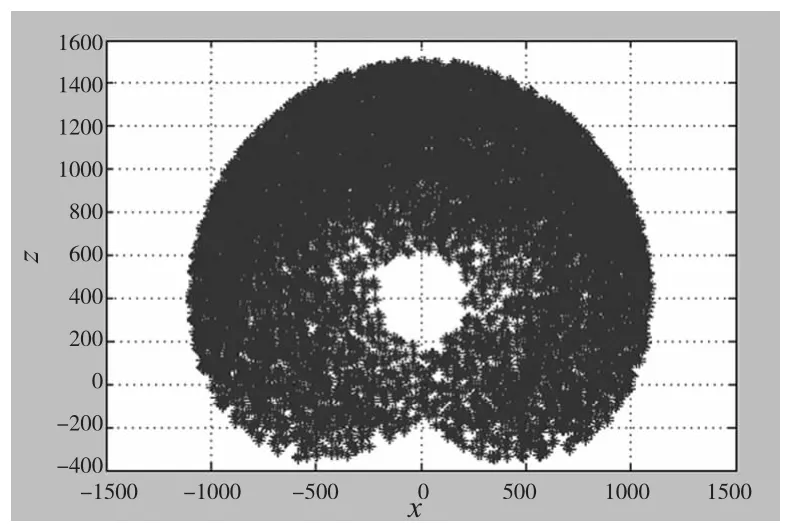
图6 xoz截面投影图

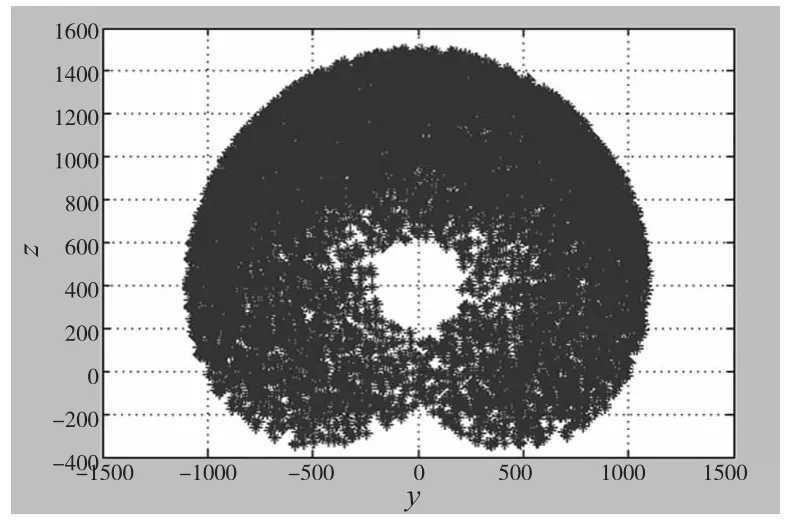
图7 yoz截面投影图

从图5、6、7可以得到该机械臂的工作空间范围是：x∈［-1100，1100］mm，y∈［-1100，1100］mm，z∈［-300，1500］mm，机械臂的可达工作空间是一个近似的椭球体构成。模拟出的空间工作符合各关节实际工作空间，空间尺寸与机械臂的本体设计参数相对应，各平面投影图上输出分布均匀没有明显空洞，工作空间形状紧凑，仿真结果与实际工作空间相符，从而验证了基于蒙特卡洛方法的机械臂工作空间分析的正确性。

4 结论

（1）应用D-H法建立了七自由度拟人机械臂的运动学模型，通过齐次变换法求解机械臂的运动学方程，获得了机械臂末端执行器的姿态向量和位置向量。

（2）根据机械臂关节空间到工作空间的映射关系，采用蒙特卡洛法，在MATLAB环境中计算出了机械臂的工作空间。模拟出的工作空间准确直观，较好地表达了机械臂的实际工作空间。从而为后续的机械臂轨迹规划、动力学分析、运动控制和参数优化提供了重要的参考依据。

［1］丁希仑.拟人双臂机器人技术［M］.北京：科学出版社，2011.

［2］王田苗，陶永.我国工业机器人技术现状与产业化发展战略［J］.机械工程学报，2014，50（9）：1-13.

［3］谭民，王硕.机器人技术研究进展［J］.自动化学报，2013，39（7）：963-972.

［4］田海波，嘛宏伟，魏娟.串联机器人机械臂工作空间与结构参数研究［J］.农业机械学报，2013，44（4）：196-201.

［5］Denavit，J.，R.S.Hartenberg.A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices［J］.ASME Journal of Applied Mechanics，1955：215-221.

［6］Rastegar J，Fardanesh B.Manipulator workspace analysis using the Monte Carlo method［J］.Mechanism and Machine Theory，1990，25（2）：233-239.

［7］Corke P I.A Robotics Toolbox for Matlab［J］.IEEE Robotics and Automation Magazine，1996，3（1）：24-32.

［8］Liegeios A.Automatic supervisory control of the configuration and behavior of multibody mechanisms［J］.IEEE Transactions on Systems，Man and Cy-bernetics，1997，7（12）：868-871.

［9］张明，何庆中，王志鹏，等.关节型码垛机器人的工作空间分析［J］.组合机床与自动化加工技术，2013（7）：68-74.

［10］YOSHIKAWA T.Manipulability of robotics mechanisms［J］.International Journal of Robotics Research，1985，4（2）：3-9.

［11］ZACHARIAS F，HOWARD IS，HULIN T，et al.Workspace comparisons of setup configurations for human-robot interaction［C］//Proceedings of 23rd IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems，IROS 2010，October 18-22，2010，Taipei，Taiwan，China. Piscataway，NJ，USA：IEEE，2010：3117-3122.

［12］ARTERMIADIS P K，KATSIARIS P T and KYRIAKOPOULOSK J.A biomimetic approach to inverse kinematics for a redundant robot arm［J］.Autonomous Robots，2010，29（3-4）：293-308.

［13］赵大兴，周小明，李九灵.集装箱喷涂机械手工作空间分析与仿真［J］.机械设计，2008，25（2）：15-17.

［14］李瑞峰，马国庆.基于Matlab仿人机器人双臂运动特性分析［J］.华中科技大学学报（自然科学版），2013，41（9）：343-347.

［15］TONDU B.Kinematic modelling of anthropomorphic robot upper limb with human-like hands［C］//Proceedings of 2009 14th International Conference on Advanced Robotics（ICAR 2009），June 22-26，2009，Munich，Germany. Piscataway，NJ，USA：IEEE，2009：1-9.

［16］MORECKI A.Biomechanics of engineering：Modelling，simulation，control［M］.Wien：Springer Verlag，1987.

［17］王智兴，樊文欣，张保成，等.基于Matlab的工业机器人运动学分析与仿真［J］.机电工程，2012，29（1）：33-37.

［18］苏学满，孙丽丽，杨明，等.基于matlab的六自由度机器人运动特性分析［J］.机械设计与制造，2013（1）：78-80.

［19］蔡蒂，谢存禧，张铁，等.基于蒙特卡洛法的喷涂机器人工作空间分析及仿真［J］.机械设计与制造，2009（3）：161-162.

［20］臧继元，刁燕，陈勇.七自由度微创手术机器人运动学及工作空间分析［J］.机械设计与制造，2010（2）：181-183.

［21］林立俊，柳和生，饶锡新，等.基于MATLAB的ARB-120型机器人运动学仿真研究［J］.组合机床与自动化加工技术，2013（3）：67-69.

［22］王跷强，王帅军，刘建亭.基于MATLAB的IRB2400工业机器人运动学分析［J］.机床与液压，2014，42（3）：54-57.

［23］刘超颖，彭发展，王占中，等.基于MATLAB的喷涂机器人工作空间分析［J］.机床与液压，2010，38（22）：6-8.

［24］赵燕江，张永德，姜金刚，等.基于Matlab的机器人工作空间求解方法［J］.机械科学与技术，2009，28（12）：1657-1666.

［25］催国华，袁会长，颜亮，等.串联机械手工作空间分析［J］.机械设计与制造，2013（10）：182-186.

（编辑 李秀敏）

Workspace Analysis of 7-DOF Humanoid Robotic Arm Based on Monte Carlo Method

HE Jia-lai，LUO Jin-liang，HUAN Peng-song，DENG Jian
（School of Mechanical Engineering，University of South China，Hengyang Hunan 421001，China）

The 7-DOF humanoid robotic arm joint coordinate systems are established and link parameters are determined by D-H method，and the robotic arm kinematics model is established.The position and orientation of robotic arm end-effector is generated by homogeneous transform method.Monte Carlo method is proposed in analyzing the workspace of robotic arm and the nephogram of robotic arm is calculated based on mapping relation from joint space to workspace of robotic arm.The reference basis is provided for follow-up robot trajectory planning，dynamics analysis，motion control and parameter optimization.

monte carlo method；7-DOF；humanoid robotic arm

TH113；TG659

A

1001-2265（2015）03-0048-04 DOI：10.13462/j.cnki.mmtamt.2015.03.013

2014-06-19；

2014-07-25

湖南省科技厅科技计划基金资助项目（2010GK3085）；湖南省重大科技专项基金资助项目（2012FJ1007）；湖南省高校科技创新团队支持计划（湘教通［2012］318号）

何价来（1989—），男，江苏常州人，南华大学硕士研究生，工程师，主要研究方向为机器人机构学、拟人机器人，（E-mail）hejialai@163. com。