考虑刀具偏摆的微铣削力理论模型分析与研究*

苏玉龙，董志国，轧 刚，刘建成，2

（1.太原理工大学机械工程学院，太原 030024；2.美国太平洋大学工程与计算机科学学院，美国加利弗尼亚 95211）

考虑刀具偏摆的微铣削力理论模型分析与研究*

苏玉龙1，董志国1，轧 刚1，刘建成1，2

（1.太原理工大学机械工程学院，太原 030024；2.美国太平洋大学工程与计算机科学学院，美国加利弗尼亚 95211）

考虑微铣削加工过程中刀具偏摆的影响，建立了一种新的未变形切削厚度计算模型，为计算微铣削力做准备。将应变梯度塑性理论引入到材料的本构方程中，利用修正后本构方程来计算微铣削过程中的流动应力。在计算微铣削力时，应用了考虑刀摆的未变形切削厚度，并同时考虑了犁切力、流动应力和弹性恢复的影响。将理论计算得出的铣削力与实验测得的铣削力进行比较，进而验证模型的可行性。

未变形切削厚度；刀具偏摆；尺寸效应；流动应力

0 引言

微切削是指对微小尺寸零件的切削加工，零件尺寸范围为0.1～10mm，几何特征尺寸范围为0.01～1mm，主要涉及微米级的特征尺寸和精度。目前，随着产品小型化的发展趋势，微切削技术在生物医学、航空航天、通信、国防以及高科技电子产品等领域有着广阔的应用前景。其中，由于微铣削具有加工任意材料和三维复杂微小尺寸零件的能力，其研究越来越受到重视。

微切削除具有宏观切削的一般特点（如大应变、高应变率以及温度变化显著等）以外，还存在尺寸效应、犁切效应和最小切削厚度效应的现象。近年来，微铣削领域的研究主要集中在对铝、铜、钢、聚合物以及钛合金等材料的可加工性和微切削机理的研究。李洪涛［1］以有限元仿真得到的稳态积屑瘤形态为基础，结合滑移线场分析方法建立综合考虑尺寸效应和最小切削厚度的铣削力模型，该模型未考虑微铣削刀具偏摆对微铣削力的影响。赵岩［2］基于金属变形机理建立考虑切削过程中金属变形的弹性回复的微铣削力模型，在计算微铣削力时未考虑刀具偏摆的影响。Mohammad Malekian［3］建立了考虑刀具偏摆，弹性恢复和犁切效应的微铣削力模型，但在计算考虑刀具偏摆的未变形切削厚度时，计算过程复杂，推导出未变形切削厚度的近似值，对计算微铣削力影响较大。Hye-RiGye［4］和许红利等人引入切削系数KT和KR来预测微铣削力，但计算过程中采用的是简化的未变形切削厚度，未考虑刀具偏摆的对微铣削力的影响。

刀具偏摆是指刀具及主轴部件的制造误差、装夹误差造成刀具轴线和主轴理想回转轴线之间漂移和偏心、以及具体加工工艺、工装等都可能产生数控铣床刀具在加工中的径向跳动。本文的刀具偏摆的大小主要取决于主轴和刀夹的制造和安装的误差。上述文献在计算未变形切削厚度时，很少将刀具偏摆考虑在内。而在微切削中，刀具偏摆量r0与刀具半径r的比值率（r0/r）比常规切削大的多，因此需要将刀具偏摆考虑在内，来研究刀尖运动轨迹。

本文考虑刀具的偏摆因素，通过数学的方法，推导出较为精确的微铣削未变形切削厚度，同时也将切削刃圆角半径处产生的犁切力、前刀面流动应力和后刀面受力的影响考虑在内，将应变梯度塑性理论引入到流动应力的研究，并且考虑刀具偏摆的影响，建立了更加有效的微铣削力理论计算模型。

1 考虑刀具偏摆的未变形切削厚度

未变形切削厚度是研究微切削力的一个重要参数。铣削加工刀齿轨迹为旋转与进给运动的合成，是一种次摆线曲线。下图1所示为两刃端铣刀切削刃的运动轨迹。

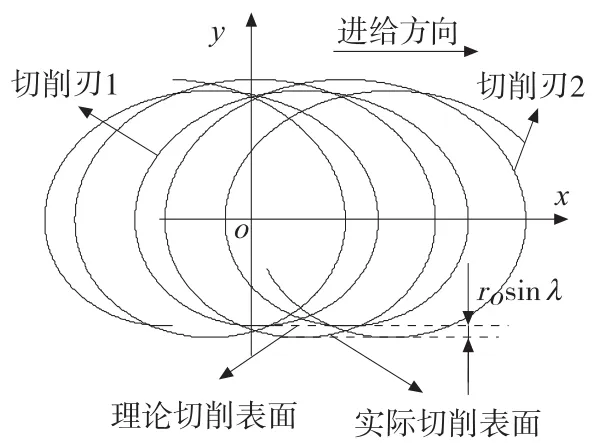
图1 端面两刃微铣刀运动轨迹

考虑微细加工中刀具摆动的影响［5］，在图1所示坐标系中，刀尖的轨迹方程为：

式中n为主轴转速，r/min；Z为铣刀刀齿数，ft为每齿进给量，μm；t为时间，s；r铣刀半径，μm；w为角速度，rad/s；z为铣刀第z个齿（取1、2），r0为刀具偏摆量，μm；λ为刀具偏摆角度，rad。

文献［3］和［5］，在计算微铣削力时，都将刀具偏摆引入计算之中，但本文在计算微铣削力时，除了考虑刀具偏摆的影响，而且还考虑了微铣削过程中的尺寸效应和犁切力的影响。文献［3］和［5］将刀具偏摆引入到未变形切削厚度的计算中，计算过程较为复杂，结果取的近似值。本文通过运用数学的方法，更加准确的将考虑刀具偏摆的未变形切削厚度公式推导出来。

将轨迹进行局部放大来研究切削厚度，如图2所示，在刀具第i个刀齿的某一位置处，将此时与X轴所成的角度设为θ0，对应时间为t0，在刀具的第i+1个刀齿的某一位置处，此时的角度设为θ1，对应的时间为t1，θ为微铣刀旋转的角度如图2所示，rad；则角度和时间存在如下关系：

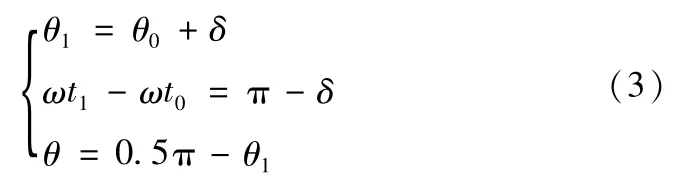
而第i齿和第i+1齿轨迹之间的部分即未变形切削厚度。

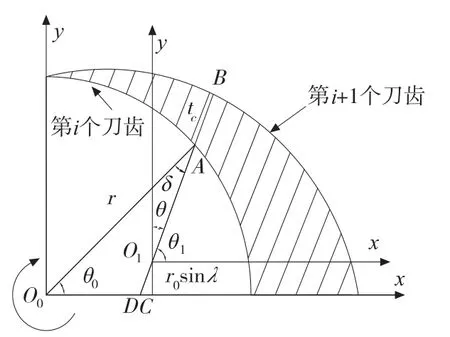
图2 未变形切削厚度

由图2根据几何关系可得：

将式（3）～（5）代入式（6）中，得到瞬态未变形切屑厚度：

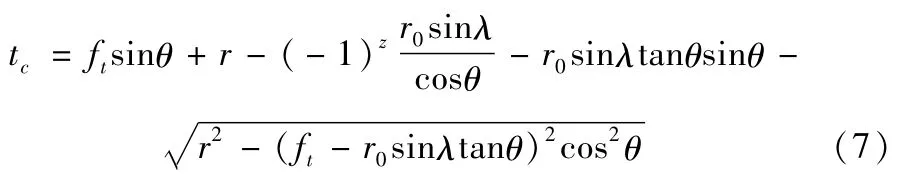
通过式（7）将刀具的偏摆考虑在内，同时未变形切削厚度也是下文计算微铣削力的一个重要参数。在计算微铣削力时，需要对tc中的θ进行积分，积分上下限分别取0和90°。未考虑刀具偏摆的为变形切削厚度为：

文献［5］中，BAO在计算未变形切削厚度时，考虑刀具偏摆的影响，但计算过程较为复杂，计算过程和结果都取得近似值，其推导出的未变形切削厚度的近似公式，如式（9）所示。

对公式（7）、（8）、（9）进行积分得到的结果如图3所示。从图3中可以看出考虑偏摆和未考虑偏摆的积分结果差别较大，BAO近似未变形切削厚度积分结果偏小，在计算微铣削力时，刀具偏摆对微铣削力的影响很大，考虑刀具偏摆是很有必要的。

图3 未变形切削厚度积分结果

2 微铣削力的理论模型

与传统的切削力模型相比，微切削需要考虑切削刃圆角半径和尺寸效应等因素的影响。微切削刃单元受力如图4所示。图中表示了切削刃产生的犁切力Fp，以及前刀面在加工过程中受到的正压力N1和摩擦力F1，后刀面在加工过程中受到的正压力N2和摩擦力F2。γn和α分别表示刀具的前角和后角，这两个参数是由刀具的几何形状决定的。γe表示刀具的有效前角，这是微细切削的一个重要特征，负前角切削。σ1和τ1分别表示前刀面的流动应力和切应力；σ2和τ2分别表示后刀面的流动应力和切应力。φ表示剪切角，θp表示犁切力的方向。

微铣削中通常采用较小的每齿进给量。随着每齿进给量的降低，导致切削厚度的降低，当切削厚度与切削刃圆角半径大小相当时，切削力中的剪切力逐渐减小，而发生在后刀面和工件之间的弹性接触力和摩擦力逐渐变大。被加工材料的变形分为无切屑形成、切屑积累和切屑形成三种情况，其变化量可用弹性恢复量S来描述。

图4 切削刃受力图

2.1 切削刃的正压力和摩擦力

切削刃前刀面所受正压力N1和摩擦力F1以及后刀面所受正压力N2和摩擦力F2分别表示为：

式中lAB、lCD分别表示前刀面剪切区刀具作用的长度（AB）和后刀面弹性恢复区刀具作用的长度（CD）。d w为铣削宽度如图9所示，定义为：

式中r表示刀具半径，μm；θ表示刀具旋转的角度，rad；β表示刀具的螺旋角，度。

2.2 剪切面的剪应力和正应力

在Liu［6］建立的滑移线模型中，认为剪切面上的应力满足Mises屈服准则，剪应力为τ1，MPa。σ1为剪切面上有效流变应力σ，MPa；σ2为后刀面的正应力，取为材料的屈服强度，MPa；切应力τ2，MPa。正应力和切应力存在如下关系：

2.3 剪切面上有效流变应力的计算

2.3.1 Johnson-Cook（J-C）材料本构模型

J-C材料本构模型已经能够有效地对宏观尺度切削过程中的大应变、高应变率和温度特性进行准确描述。该模型中流动应力与材料的应变、应变率效应、温度效应有关，其表达式为：

J-C模型将材料流动应力表示为三项的乘积，分别表示材料应变硬化、应变率硬化和温度硬化，式中：A、B、C、m和n为待定参数，可以通过实验拟合得到。T，T0和Tm分别为材料变形温度（取剪切面平均温度）、环境温度（25℃）和材料熔点。参考文献［7］，为参考应变速率取为1s-1。

2.3.2 J-C本构模型的修正

结合Oxley-Welsh切削理论可设剪应变为：

将式（12）、（14）代入式（13）中，可将本构方程用剪应力和剪应变来表示：

剪应变速率为：

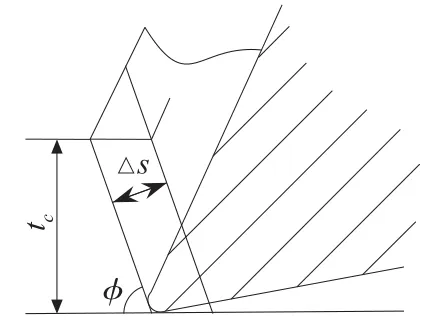
图5 剪切区变形简图

在微铣削中出现了明显的尺寸效应现象，即切削比能随未变形切削厚度的减小而非线性增大的现象。宏观切削的J-C模型不再适用，本文采用J-C的修正模型，引入应变梯度理论，应变梯度塑性理论将材料剪切流动应力表达为位错密度的函数，认为材料的塑性硬化来源于统计存储位错与几何必需位错，前者与塑性应变有关，后者与塑性应变梯度有关。应用应变梯度塑性理论可以成功预测微铣削中的尺寸效应。修正模型［9］如下：

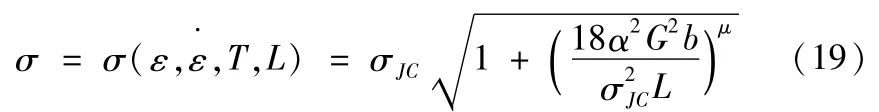
式中，G为材料的剪切模量，MPa；b为Burgers矢量为1/10纳米级；μ为修正系数，α为材料系数取0.2～0.5；L为剪切区的长度如图6所示，μm；计算公式如下：

图6 微细切削切屑形成

L用于计算考虑尺度效应的J-C本构方程中的有效流动应力；剪切面上的有效流动应力用于计算前刀面的正压力和摩擦力；弹性恢复量用于计算后刀面工件的接触长度，进而计算后刀面的作用面积，从而计算出后刀面的正应力和摩擦力。

工件材料选用无氧铜，利用公式（19）进行加工无氧铜剪切面上有效流动应力的计算，材料力学性能如表1所示，利用MATLAB进行计算，计算出不同的主轴转速和不同的未变形切削厚度对应的剪切面有效流动应力，结果如图6所示。

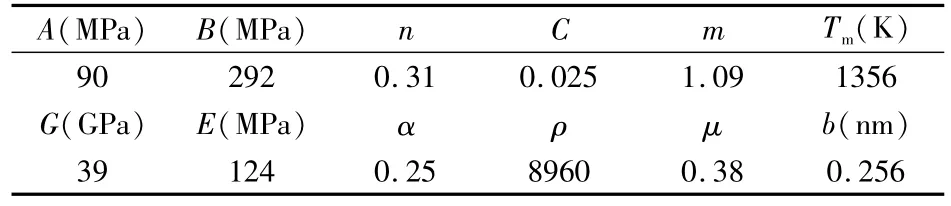
表1 无氧铜材料力学性能参数表

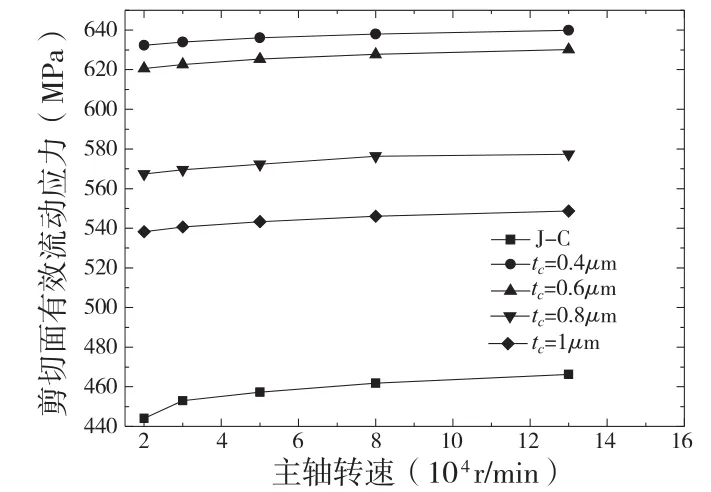
图7 不同切削参数剪切面上的流动应力

从图7可以看出，主轴转速和未变形切削厚度都会影响剪切面的有效流动应力。当主轴转速一定时，未变形切削厚度越大，有效流动应力反而越小。当未变形切削厚度继续增大，有效流动应力曲线逐渐向宏观J-C模型靠近。当未变形切削厚度一定时，主轴转速越大，剪切面处的有效流动应力也越大，但是增大的幅度较小，说明主轴转速对剪切面的流动应力影响较小。

利用ABAQUS仿真验证剪切面处的有效流动应力，无氧铜的参数如表1所示，刀具参数如表2所示。

表2 刀具参数表

仿真结果如图8所示，图8表示利用修改后J-C本构方程进行模拟仿真，左图表示未变形切削深度tc=0.8μm，剪切面处的有效流动应力为580MPa，右图表示轴向切削深度为20μm，每齿进给量为0.4μm，主轴转速为50000r/min，剪切面的有效流动应力为650MPa，和计算的结果基本吻合。

图8 ABAQUS仿真应力云图

2.4 切削刃圆角处的犁切力

微铣削过程中切削刃圆角处存生犁切效应，工件材料受到切削刃圆角的挤压，产生犁切力FP，如图4所示。由维氏硬度的定义，可推导出犁切力FP与材料的维氏硬度H，MPa；满足如下关系：

根据文献［10］，K为系数，与切削厚度有关；Sp为接触面积，μm2，可以表示为：

式中，α为刀具后角，度；γe为刀具的有效前角，度；r表示切削刃半径，μm；w表示铣削宽度，μm。

由文献［11］，Tabor提出的理想弹塑性材料的有效流动应力σ和硬度H之间存在线性关系，材料系数取3，有：

将式（22）、（23）带入式（21）得犁切力为：

令θp为犁切力的方向角，如图4所示，计算公式如下：

式中，γn为刀具的名义前角，度。

2.5 弹性恢复量与弹性恢复率

由文献［2，12］，弹性恢复量S表示后刀面处被加工材料的变形量，μm；

其中k为弹性恢复率可由以下公式求出。

式中，tmin为最小切削厚度，μm；te为参考切削厚度，μm；计算公式如下：

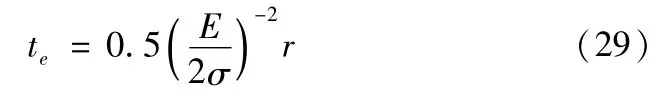
2.6 切削刃的切向和径向分力

由图4分析，切削刃的切向力d Fc和径向分力d Ft为：

式中，φ为剪切角，ζ为变形系数，tc为未变形切削厚度，μm；t切屑的厚度，μm。

为了计算微切削力和径向力，需要将上文的未变形切削厚度tc、切削刃处的犁切力、前刀面的流动应力σ和后刀面处的摩擦力和正压力代入求解切向力d Fc和径向分力 d Ft的公式中。即将式子（7）、（10）、（11）、（19）、（24）和（27）带入式子（30）、（31）中，得到径向和切向的微铣削力公式：

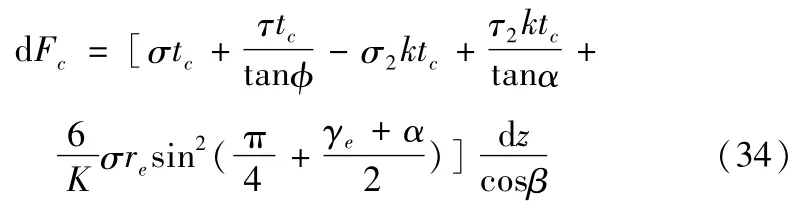
轴向力d Fz与切向力d Fc之间的关系如图9所示为：

将径向力和切向力转换为X轴和Y轴方向的铣削力：

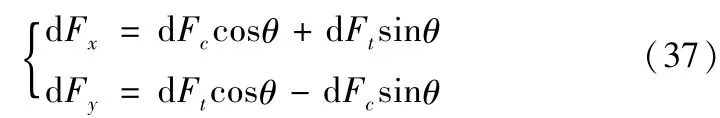
对上式（37）进行积分即可求出Fx和Fy的大小，公式如下：

3 微铣削力模型的实验与分析

采用文献［1］对无氧铜的微铣削实验进行理论模型的验证分析，文献［1］中的实验设备全采用进口的设备，精度相对较高，实验数据较多，并且实验数据也比较准确，被广泛的采用。

3.1 考虑刀具偏摆和未考虑刀具偏摆对微铣削力的影响

由上面建立的微铣削力理论模型分别计算轴向切削深度为15μm，主轴转速为20000r/min，每齿进给量为0.2μm、0.4μm、0.6μm、0.8μm、1μm时的铣削力，与文献［1］在相同条件下用实验测出的力进行比较，轴向切削深度分别为15μm，利用公式（34）、（35）和（38）可以计算，不同的每齿进给量对微铣削力的大小的影响，结果如图10所示。

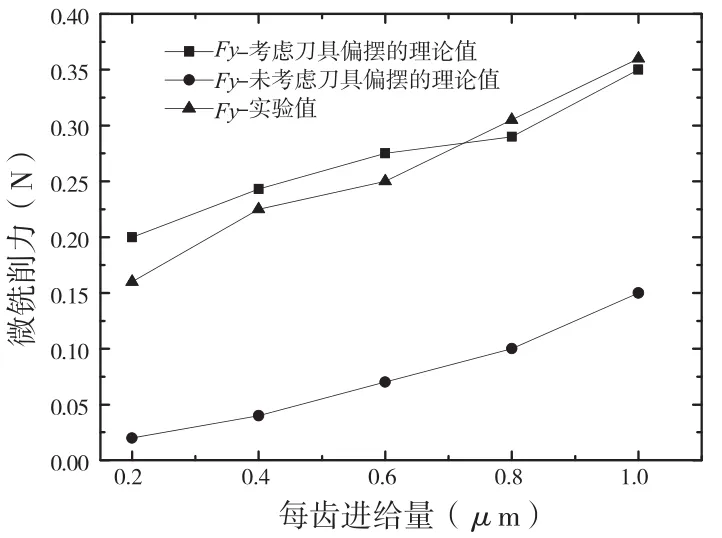
图10 轴向切深15μm微铣削力变化图

从图10可以看出，当每齿进给量小于0.7μm时，理论值大于实验值；当每齿进给量大于0.7μm时，理论值小于实验值。未考虑刀具偏摆和考虑刀具偏摆计算出的微铣削力差别很大，从图10可以看出，考虑刀具偏摆计算的结果更接近于实验值。

3.2 轴向切削深度对微铣削力的影响

主轴转速为20000r/min，每齿进给量为0.2μm、0.4μm、0.6μm、0.8μm、1μm分别取轴向切削深度为15μm和20μm进行计算，结果如图10，图11所示。

图11 轴向切削深度为20μm对微铣削力大小的影响

从图10和图11中可以看出，轴向切削深度一定时，微铣削力随着每齿进给量的增大而增大，并且微铣削力增大的幅度也较大；考虑刀具偏摆和未考虑刀具偏摆计算出的微铣削力差别较大，从图中可以看出，考虑刀具偏摆计算出的力更接近实验值。

3.3 切削速度对微铣削力的影响

取轴向切削深度为20μm，每齿进给量为1μm，主轴转速分别为20000r/min，30000r/min，50000r/min，80000r/min，130000r/min，将以上参数带入公式（34）、（35）和式（38）中，计算出不同切削速度对微铣削力大小的影响。

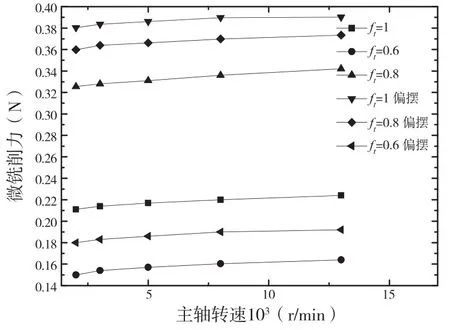
图12 不同转速对微铣削力的影响

图12 表示了随着主轴转速的增大，微铣削力也呈现增大的趋势，但是从图中可以看出，其他条件不变，主轴转速对微铣削力的影响很小；图12也表示出主轴转速一定时，随着每齿进给量的增大，微铣削力也随着增大，并且增大的程度较大；每齿进给量一定时，考虑刀具和不考虑刀具偏摆所计算出的微铣削力差别较大，考虑刀具偏摆的计算的微铣削力要大于未考虑刀具偏摆的。

通过对图10～图12数据进行分析，每齿进给量、主轴转速和轴向切削深度对微铣削力的大小都有影响，但是影响程度不同。每齿进给量对微铣削力的影响程度最大，轴向切削深度的影响次之，主轴转速对微铣削力的影响最小。

4 结论

本文建立的微铣削力的理论模型，采用了考虑刀具偏摆的未变形切削厚度，并且研究了尺寸效应对微铣削力的影响。

（1）考虑刀具偏摆和未考虑刀具偏摆的未变形切削厚度积分之后结果相差较大，对微铣削力的影响也较大，所以微铣削不能忽略刀摆的影响。

（2）当每齿进给量小于30%的切削刃半径时，犁切力占主导地位；当每齿进给量大于30%的切削刃半径时，剪切力占主导地位。

（3）利用修正后的J-C本构方程进行剪切面处的有效流动应力的计算，将结果导入到ABAQUS中，进行仿真，得到不同切削参数条件下，剪切面的有效流动应力，然后代入公式，得到更加准确的微铣削力。

（4）每齿进给量、主轴转速和轴向切削深度对微铣削力的大小都有影响，并且每齿进给量的影响最大，主轴转速对微铣削力的影响最小。

［1］李洪涛.介观尺度材料力学性能建模及微铣削工艺优化研究［D］.上海：上海交通大学，2008.

［2］赵岩.微细铣削工艺基础与实验研究［D］.哈尔滨：哈尔滨工业大学，2008.

［3］Mohammad Malekiana，Simon S.Park，Martin B.G.Jun. Modeling of dynamic micro-milling cutting forces［J］.International Journal of Machine Tools&Manufacture，2009，49（7）：586-598.

［4］Hye-RiGye，Byeong-Uk Song，Yong-Seok Lim，et al.Prediction of Cutting Force and Tool Deflection in Micro Flat End Milling［J］.International Journal of Materials，Mechanics and Manufacturing，2013，1（1）：13-16.

［5］W Y Bao，IN Tansel.Modeling micro-end-milling operations.Part II：tool run-out［J］.International Journal of Machine Tools&Manufacture，2000，40（15）：2175-2192.

［6］X Liu，M B Jun，R E Devor.Cutting Mechanics and their influence on dynamic forces，vibrations and stability in micro-end-milling［J］.Proc.of ASME Manufacturing Engineering Div，Anaheim，2004，15（2）：583-592.

［7］S P F C Jaspers，J H Dautzenberg.Material behaviour in conditions similar to metal cutting：flow stress in the primary shear zone［J］.Journal of Materials Processing Technology 2002，（122）：322-330.

［8］严宏志，龚黎军.20CrMo材料本构模型及其有限元模拟［J］.中南大学学报（自然科学版），2012，43（11）：4268-4273.

［9］Xinmin Lai，Hongtao Li，Chengfeng Li，etal.Modelling and analysis of micro scale milling considering size effect，micro cutter edge radius and minimum chip thickness［J］.International Journal of Machine Tools&Manufacture，2008，48（1）：1-14.

［10］吴继华.基于应变梯度塑性理论的正交微切削变形研究［D］.济南：山东大学，2009.

［11］D.Tabor.The hardness of metals［M］.Oxford：Oxford U-niversity press，2000.

［12］V Jardret，H Zahouani，J L Loubet.Understanding and quantification of elastic and plastic deformation during scratch test［J］.Wear，1998，218（1）：8-14.

（编辑 李秀敏）

Study on Cutting Tool Running out Considered Theoretical Analysis Model for Cutting Force Estimation in Micro End Milling Process

SU Yu-long1，DONG Zhi-guo1，YA Gang1，LIU Jian-cheng1，2
（1.College of Mechanical Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.School of Engineering and Computer Science，University of the Pacific，Stockton California 95211，USA）

In this paper，a new nominal uncut chip thickness estimation algorithm for micro-scale end-milling is proposed，in which the combination of an exact trochoidal trajectory of the tool tip and the tool running-out is considered.The strain gradient plasticity theory is introduced into the constitutive equation of material to calculate the flow stress in the process of micro end milling.The uncut chip thickness is applied to calculate the cutting forces，where the influence of plough shear，the flow stress and the elastic recovery are considered.The calculated results show a satisfactory agreement with the results obtained from cutting experiments.

uncut chip thickness；tool run-out；size effect；flow stress

TH122；TG506

A

1001-2265（2015）03-0038-06 DOI：10.13462/j.cnki.mmtamt.2015.03.011

2014-06-26；

2014-08-05

山西省自然科学基金项目（2005-1051）

苏玉龙（1989—），男，山东荣成人，太原理工大学硕士研究生，研究方向为微细铣削加工，（E-mail）suyulongjiang@sina.com；刘建成（1964—），男，美国太平洋大学机械工程学院终身教授，博士研究生导师，研究方向微细制造。