社交网络结构特性分析及建模研究进展*

文/许进　杨扬　蒋飞　金舒原北京大学信息科学技术学院 北京 0087 2中国科学院计算技术研究所 北京 0090

社交网络结构特性分析及建模研究进展*

文/许进1杨扬1蒋飞1金舒原2**
1北京大学信息科学技术学院 北京 100871 2中国科学院计算技术研究所 北京 100190

当前我国互联网信息安全形势严峻，在社会舆情预警、隐私泄露保护等方面具有重大需求。在线社交网络由于其承载着海量的信息，是信息安全研究的重要对象。本文从作为理论基础的社交网络结构属性和模型展开综述，其中包含作者所在研究团队的成果及观点。社交网络的结构特性的研究重点在于揭示社交网络的基本属性、探索作为社交网络基本要素的人与人之间的关系的本质特征；社交网络模型研究重点在于通过模拟真实社交关系网中人与人之间的交往行为来构造具备相应属性特征的演化模型，并以此为基础，研究特定社交行为对网络结构的影响，或者通过所建立的模型逆向分析社交网络的本质特征、推断哪些社交行为决定着相应的网络特性。近年来，不同的策略和技术分别在网络的结构特征、网络中的信息传播和检索、网络中用户的行为分析、社团结构挖掘等领域取得了重大研究进展。文章对网络结构研究中取得的成果进行了回顾，分别介绍了近期研究中所发现的社交网络在不同层面表现出的结构特征，并给出了社交网络模型研究中几类常见的结构模型和建模方法。

社交网络，网络结构，结构特征，结构建模

DOI 10.16418/j.issn.1000-3045.2015.02.009

1　引言

互联网在不断发展，人类社会已经进入了大数据时代，而社交网络是大数据的重要载体。海量信息在社交网络中的产生、利用及传播，引发诸多信息安全问题，如个人隐私泄露、道德诚信危机、社会问题激化等。社交网络是信息安全的基石，对社交网络的研究和利用已经成为各国政府及科技工作者的研究核心。

社交网络是一种典型的复杂网络，其中存在着复杂的用户群体互动行为。与交通网络、通讯网络和生物网络等其他复杂网络相比较而言，社交网络包含了更加海量和多元化的信息。在这些信息中，网络的结构信息十分重要：首先，它直观地反映了用户间通过相互关注建立的朋友关系，构成了网络中信息来往沟通的物理基础；其次，面向网络结构的研究不但可以印证在其他领域所发现的人类社会行为特征，如“富人俱乐部现象”等，还帮助人们发现新的社会行为规律，如社交群体中的社团聚集现象等；最后，由于网络结构是社交网络个体间信息传播的载体，因而与用户发表并传播文本内容等行为相关的用户话题建模、文本信息检索、影响力最大化问题等研究极大地依赖于对网络结构的深刻认识。可以说，社交网络的研究基础起始于对其网络结构的研究。

社交网络具有复杂网络的基本结构特征。将构成社交网络的基本要素的人作为节点，人与人之间的关系作为节点之间的连线（或称为连边），社交网络就可以用一个复杂图来描述。与其他类型的复杂网络不同的是，社交网络由于其连边中所固有的社会性，表现出一些独特的结构特性，如“小世界”现象、“同配性”现象等。

社交网络的结构研究通常分为特征发现与结构建模两部分。社交网络的特征发现研究着眼于对其包含的大量的节点和边的规律研究，通过观察这些基本构成元素的组织规律，得到网络的基本属性和特征；社交网络的结构建模研究相应结构特征的形成机理，帮助人们对网络结构产生更深刻的理解，并可用于预测网络的下一步演化形式。

2　国内外研究进展

2.1社交网络的结构特性

理解社交网络最直观的方法是观察其拓扑结构。随着在线社交网络用户日益增多，通过可视化的方式来研究社交网络在很多情况下并不适用。近年来，大量工作关注于研究社交网络的统计特性。统计特性的发现不仅可以让我们更加有效地关注于社交网络的整体特点，而且它对社交网络中个体行为分析、信息传播、舆情发现及预警等关键的应用问题有着至关重要的推动作用。

下面，我们分别对社交网络中重要的统计特性进行综述，并在最后论述合作行为与网络结构特性演化的关系。其中，社交网络的小世界现象，使得人与人之间的去中心化搜索更加容易；社交网络的无标度特性，使得信息得以快速传播、随机删除节点不影响网络的连通性；不同的中心性评价指标，有助于快速发现核心节点；同配性及其演化规律的发现，有助于理解人与人之间的交友方式；社交网络中的社区结构，有助于人们认识其所处的环境。

2.1.1小世界现象与无标度特性

早在20世纪60年代，美国哈佛大学教授米尔格兰姆（Milgram）通过一个信件投递实验提出并验证了“六度分隔”理论［1］。与“六度分隔”理论不同的是小世界网络不仅具有较小的平均距离，还有较高的集聚系数。1998年，复杂网络领域著名研究学者沃茨（Watts）和斯特罗加茨（Strogatz）发现许多网络中都存在小世界现象［2］。小世界特性中包含了2个重要的属性，即网络平均路径长度、平均聚集系数。网络中节点之间的平均距离，通常用平均路径长度进行刻画。平均聚集系数（Clustering Coefficient）描述了任取一个节点，它的邻居也互为相邻节点的概率。研究表明，大多数不同种类的社交网络中都存在小世界现象［3］，如知名的社交网络Flickr、YouTube、LiveJournal等。具有小世界现象的社交网络可以用于快速的去中心化搜索［4］。

1999年，美国著名复杂网络科学家巴拉巴斯（Barabasi）和艾尔伯特（Albert）发表在国际顶级期刊Science上的文章揭示了许多复杂网络都具有无标度特性［5］。无标度特性引起了各学科的广泛关注，目前该文章的谷歌引用次数已经高达2万余次。无标度特性指的是网络中的度服从幂律分布，即P（k）∞k-γ，γ为幂律指数，P（k）表示网络中度为k的节点在整个网络中所占的比例。小世界现象和无标度特性的发现也掀起了网络结构特性研究的新高潮［4，6，7］。随后的研究表明，社交网络具有无标度特性［3］，即绝大多数用户拥有较少的社会关系，极少数用户存在较多的社会关系。无标度特性的存在使得社交网络具有很多独特的性质，如去中心化搜索的高效性、信息传播的可控制性等。

2.1.2网络弹性

与度分布相关的一个重要现象是网络弹性（Network Resilience）。大多数网络体现的功能都依靠自身的连通性。如果将网络中的某些节点移除，可能导致其他节点之间的距离增加，甚至使得整个网络不再连通，从而破坏网络的功能。网络弹性是指网络承受破坏的能力，具体为删除节点或者边对网络连通性的影响程度［8］。

对于不同的删除节点方法，网络也表现出不同的弹性。例如，随机删除网络中的节点或者删除某些特定的节点。艾尔伯特（Albert）等人［9］研究了2个顶点度近似服从幂律分布的网络的弹性。他们以节点间的平均距离为指标，揭示了两种删除节点的方式分别对网络弹性的影响。结果表明，随机删除节点对平均距离几乎没有影响，而依次删除度最大的节点使得平均距离急剧增加。

为了衡量节点对网络弹性所起到的作用，博尔加蒂（Borgatti）等人［10］提出通过度中心性，介数中性和紧密度中心性进行衡量。威姆斯（Wehmuth）等人［11］提出一种基于谱分析的分布式算法来确定重要节点。克玛瑞克（Kermarrec）等人［12］采用随机游走的方法衡量节点重要性。格鲁贝斯克（Grubesic）等人［13］首次研究了从物理上关闭某些互联网基础设施对整个网络产生的影响，指出目前的互联网基础设施拓扑结构不能很好地应对紧急问题。

2.1.3核与核度

网络的核与核度（Core and Coritivity）是国内提出的评价网络连通性、抗毁性的重要指标［14］。一个网络的核是这样一类节点的集合，删除该集合中的节点会使网络产生最大的连通分支增益。连通分支增益定义为产生的连通分支数减去节点集合的大小。这个最大的连通分支增益即为核度。核与核度的数学定义为：设G是一个网络，它的顶点集合为V（G），则称为网络G的核度，满足上式的节点集S为网络G的核。核与核度的理论不仅可以很好地用于评价网络的连通性，也可以被用于发现社交网络中有影响力的节点［15］。

2.1.4中心性

研究社交网络中心性的倾向性规律对网络结构演化预测、病毒营销、信息传播等都有着重要的意义。在社交网络的研究中，中心性（Centrality）是度量节点重要性的指标。某个节点的中心性有多种度量方法，分别是度中心性、介数中心性、紧密中心性和核数。节点的度中心性定义为节点的度与最大可能的度的比值。介数用来描述网络中节点承载最短路径数的能力，节点的介数等于网络中所有最短路径中经过该节点的概率之和。节点的紧密度定义为节点到其他所有节点的最短路径之和的倒数乘以其他节点个数。一个网络中的k-核（k-core）指的是反复去掉该网络中度小于或等于k的节点及其关联的边后，剩余的子图。一个节点的核数等于k，当且仅当这个节点存在于网络的k-核中且不存在与（k+1）-核中。k-核可以用来表征社交网络中的层次结构，揭示社交网络的结构［16］。马克纽曼（Mark Newman）［17］分析了各种中心性的特点和适用场合。狄萨科（Kitsak）等人［18］分析了不同网络中最有影响力的节点，提出k-core比介数和度中心性更适合描述节点的中心性与影响力。赫尔瑟芬（Holthoefer）等人［19］在传播模型中选择不同核数的点作为初始节点，发现核数更大的节点在阻隔信息传播方面有着更大的作用。霍姆（Holme）等人［20］论证了网络节点的中心性与网络脆弱性之间的联系。

2.1.5同配性

网络的同配系数（Assortativity Coefficient）反映了网络中度相近节点间相互关联的程度［21］。同配系数大于零表明网络中相互连接的节点之间的度是正相关的，即度大的节点倾向连接度大的节点，而度小的节点的邻接节点普遍具有较小的度。这样的网络被称为具有同配性（Assortativity）。反之，网络是异配的。

2002年，纽曼（Newman）等人［22］发现大多数社会网络是同配网络，如科学家合作网与电影演员合作网。2009年，国内研究学者发现在线社交网络的同配性并不是固定不变的，它往往存在着演化过程［23］。在线社交网络建立初期通常存在同配特征，随着用户群体规模的扩大，同配性逐渐演化为异配性。这是由于在线社交网络初期的用户通常由最先加入的用户介绍而来，在一定程度上还原了线下的社会网络关系，体现出同配特征。随着用户数量的增加，现实世界中的名人在网络中通常会吸引大量普通用户优先与之连接，从而导致网络呈现异配特征。2012年，尼尔（Neil）等人［24］研究了在线社交网络Google+从内测到开放这几个月的数据，发现其同配系数存在由正变负的演化规律。博伦（Bollen）等人［25］调查了现实社会网络与在线社交网络同配性之间的关联。他们跟踪了6个月的Tweet记录，结果表明在线社交网络的同配性变化对社会网络有一定影响。贝内文托（Benevenuto）等人［26］利用同配性对YouTube的用户进行了分类。

2.1.6社区结构

社交网络的研究中，社区发现问题是十分重要并且被广泛研究的问题［27-29］。社区结构广泛存在于社交网络中，一个社区可能代表具有共同兴趣、爱好、目标的群体［30］。社区发现有着很好的应用前景，用在如网络营销、用户推荐、影响力评估、个性化搜索等重要的应用中。社区结构有助于我们在中观层面上理解社交网络的本质。

尽管社区结构十分重要，但是现在并没有普遍承认的统一定义。一般，我们认为社区由一组节点组成，社区内的节点之间连接较紧密，社区之间的节点连接较疏松［31］。社交网络中往往存在重叠社区，即允许一个节点加入多个社区。

大量的方法和技术被应用在社区发现算法的设计中，如基于团渗透的算法［27，32］、线图算法［28，33］、模块度优化算法［34］、局部优化算法［35］等。近年来，基于模型的统计学习方法也被应用在社区发现问题上［36，37］。但是每种方法都有各自的局限性。团渗透算法不能发现低密度的社区；基于模块度优化的社区发现算法，具有分辨率局限性，容易合并较小规模的社区［38］；基于线图的算法，需要将原图进行转化，并且相似度的量化对于社区发现的结果影响较大；局部优化和节点扩张的算法，初始节点的随机选择使得社区发现的结果不稳定；基于模型的统计学习方法，参数估计的速度较慢，无法应用于大规模网络。社区发现领域目前的研究热点是社区的演化分析、大规模网络的社区发现、基于流图的社区发现以及异质网络、伙伴网络的社区发现。

2.1.7合作行为与网络特性的关系

2012年，哈佛大学、剑桥大学的研究人员对在坦桑尼亚的哈扎人（Hadza）的社交网络进行了研究［39］。哈扎人携带着古代的DNA，并且沿袭着打猎采集的古代生活方式。研究人员造访了17个哈扎人营地，对其中全部的205个成年人进行了详细研究。他们通过调查的方式，建立了两个网络：一个是Campmate有向赋权网络，调查如果营地重新组合，每个人想和谁一个营地，用来表示每个人的社交积极性（Active）和吸引性（Attractive）；另一个是Gift有向赋权网络，用来调查每人愿意赠送出多少食物给不多于3个同伴（图1）。通过对这些网络的研究，研究者发现这些网络也拥有现代社交网络的特性，其中包括异质度分布、度的同配性、高聚集系数、互惠性、同质性。研究者还在他们中进行了公共品博弈（public goods game）。

图1　Campmate网络和Gift网络。节点不同的形状、灰度代表不同的性别和捐赠的数量。有向边所指的是被选择的人或被捐赠者，边的颜色代表节点之间的关系［39］

每个人都被赋予了4份食品（蜂蜜，是哈扎人最喜欢的食物），他们可以选择自己占有或者贡献出来。如果有人将一定数量的食物贡献出来，那么研究者会把食物数量乘以3倍，然后分给参与的所有人。公共品博弈的社会最优策略是所有人都贡献出自己的食物。而纳什均衡点是全部自己占有，即自私策略就是每个参与者的最优策略。面对最喜欢食物的诱惑，哈扎人并没有选择自私，而是选择了合作，平均每人贡献出了超过一半的食物。这个实验显示出了和其他现代小规模社区一致的结果，即倾向于合作，而不是被纯粹的自私策略所控制。

在哈扎人网络中，从合作的层面上来讲，合作者之间有较强的同质性，即合作者之间的建立关系的概率要大于合作者与非合作者之间建立连接的概率。由于能够获得更多的食物及更多的帮助，具有合作行为的个体较之非合作行为的个体可以更好地生存和繁衍。以上这些结果表明，现代社交网络结构的一些特性在人类早期社会就已经存在了。社交网络对合作的产生和演化起了很重要的作用，并且合作行为表现出的同质现象也促进了社交网络的发展。

2.2社交网络结构建模

社交网络结构建模是在社交网络结构特性分析的基础上，对其形成机理和演化规律认识的验证和深化。常见的模型可分为两大类，一类是网络构造模型，通过显式地设定网络中节点的加入和边的形成过程来构建网络，这类模型的优点在于过程直观并可形象地模拟人类社交行为，缺点在于参数求解比较困难；另一类模型是采用统计建模方法的随机生成模型，将复杂的网络结构生成过程简化为若干基本概率步骤，并通过统计推断得到模型参数以还原这个生成过程，这类模型能够从宏观层面对网络结构的形成机制进行解释，然而却不如构造模型直观和具体。

2.2.1网络构造模型

网络构造模型经历了一个由ER随机图模型到小世界、无标度模型的演化过程。其中ER随机图模型由知名数学家厄尔多斯（Erdos）于1960年提出［40］，该模型通过假设网络中所有潜在边都具有独立同分布生成概率的，成功刻画了网络中节点间连边的无序性，并在接下来近40年的时间里深刻影响着人们对复杂网络现象的认知。

随着现代电子计算机技术和互联网的发展，人们得到了更加强大的数据分析工具，并接触到了更多类型的复杂网络数据，如以万维网和电子邮件网络所代表的科技网络［41］、以科研合作［42］和演员合作关系［43］所代表的社交网络、以道路运输网络代表的交通网络［44］等。在实验中，人们发现ER随机图并不能有效解释复杂网络中的一些常见现象，如通过该模型生成的人工仿真网络并不具有平均路径长度较短，聚集系数较高和节点度分布服从重尾分布的特征等，而这些规律在真实世界的网络中是普遍存在的。由此，人们需要通过新的网络模型刻画这些网络结构。在世纪之交，2个具有里程碑意义的工作分别见诸于Nature和Sci⁃ence，其中WS模型［2］通过对规则栅格网络中的边进行概率重连接的方法，构造出了参数特征介于规则网络和ER随机网络之间的小世界网络，该网络具有较高的聚集系数与较短的平均路径长度，并在一定程度上解释了小世界现象的形成要素，而BA模型［5］通过引入“择优连接”机制，构造出了具有无标度特征的网络结构，解释了导致网络产生重尾效应的客观规律。类似地，人们围绕小世界现象和无标度特征还建立了不同的模型，其中最主要的一类是基于“择优连接”机制展开的［43，45-47］，这些模型都通过将新的节点加入网络来扩增网络规模，并以择优连接机制建立网络中的连接。然而这类模型的共同问题在于其网络直径是缓慢增长的，这与实际网络中常见的“直径缩减”特性相悖［48，49］。由于这些模型通常是显式地给出了网络的生成机制，因而难以估计模型的相关参数，或者进行这种估计的价值是不大的，这就解释了为什么很少能看到将其与观测数据进行拟合和进行参数估计的工作。

上述工作的共同问题在于，模型都只注重于刻画网络中的一个或少数几个静态特征，并由于模型不存在显式解，造成了参数估计比较困难，而Kronecker图模型则有效克服了这些问题。莱斯科韦茨（Leskovec）等人［50］发现可以用矩阵的Kronecker乘积操作来生成网络，将两个图之间的Kronecker积定义为它们的邻接矩阵的Kronecker积，就可以进行图的扩展操作，并且扩展生成的图具有自相似的特性。整个模型的生成过程是对一个初始图K1，进行（i-1）次Kronecker积操作，最终形成Ki。由于该方法具有独特的递归构造形式，因此Kronecker图模型所生成的网络具有良好的可分析性，并且对于具有成百上千万节点规模的巨大网络，仍然能够较为容易地得到模型的参数估计值。实验中发现，Kronecker图模型生成的网络可以很好地模拟静态网络的度分布、特征值分布以及动态网络的直径、密度变化的幂律分布等特性。而这些优良特性是前述模型所不具备的。

上述模型的提出，大都是由相关研究人员根据网络结构的静态特征，基于经验假设并设计相应算法来实现的。另外一种建模的方法是：首先观察真实世界的网络演化过程来分析用户行为规律，进而在模型中设定相应的规则来模拟这些行为。这类模型建立了用户行为与网络结构演化之间的关联，能够帮助分析人类的社交行为对网络结构的影响。莱斯科韦茨（Leskovec）等人［50，52］观察到用户加入网络后连接到邻居的邻居这一行为规律，提出了森林火灾模型。在该模型的演化过程中，度高的节点更容易被新增的节点连接，并且递归调用过程使得新增节点可以形成很多边，导致了入度与出度的重尾分布。新加入的节点与代表节点的邻居形成许多有向边、网络中形成社区、新增节点在代表节点社区附近形成许多连接等原因造成了网络的密度以及有效直径的变化。这些都是与真实网络中观察到的规律相符的。区别于其他研究网络统计属性的模型，库玛（Kumar）等人［51］将网络中的用户分为Passive、Linker和Inviter三类，新加入的节点被随机地指定为三类节点中的一种。在添加边时，首先按照择优连接原则从网络中已有的Inviter和Linker节点中选择一个作为边的源端。如果源端是Inviter节点，则新增一个节点作为边的终端与其相连；如果源端是Linker节点，则从已有的Inviter和Linker节点中按照择优连接原则选出一个作为边的终端。按照该模型产生的网络与观察到的Flickr和Yahoo！360°的3部分构成相符，能够产生具有巨大分支、孤立社区和孤立节点（图2）。

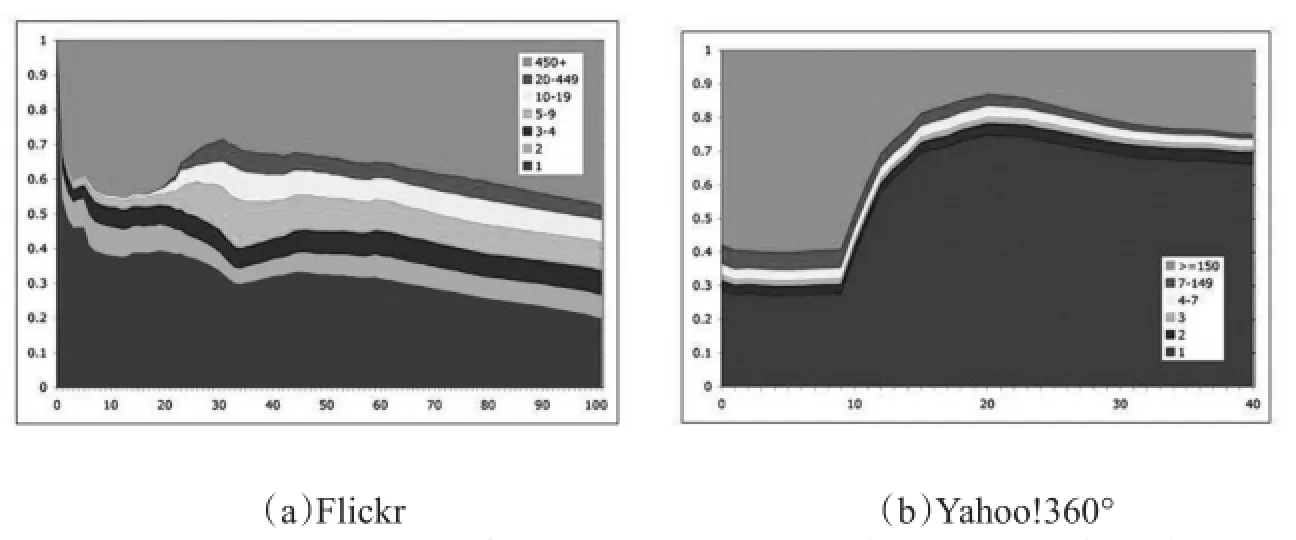
图2　Flickr和Yahoo！360°中不同大小的组成部分节点所占比例（按周）［51］

Leskovec等人［52］对4个真实社交网络的演化过程进行了观察和研究，总结了用户的行为规律，并在模型中进行重现。他们提出的网络完全演化模型包含了节点到达、边初始化以及边端点选择过程。其中边初始化过程中使用了节点生存时间以及“睡眠”的概念：对于网络中的节点，按照其度的某个指数函数产生一个时间间隔δ并进入睡眠状态δ个时刻，当其从睡眠状态中苏醒时，如果生存时间还没有到期，则使用随机-随机三角闭合模型产生一个长度为2的边（即随机选择该节点的一个邻居，然后随机选择该邻居的一个邻居，然后将该节点与选择的邻居的邻居相连形成一个长度为2的边）。如果一个节点的生存时间到期了，则该节点就要停止增加边；否则继续执行睡眠-苏醒这一过程。该模型生成网络的聚集系数、度分布、最短路径长度等参数都与Flickr等真实网络相近，因而可被用来生成任意规模的人工合成网络。

2.2.2随机生成模型

另外一类重要的结构模型是随机生成模型，这类模型不考虑网络中具体节点和边的生成过程，而是将形成网络观测数据的复杂机制简化为几个基本的概率步骤。先假定网络的观测数据由一个潜在的概率统计过程生成，然后通过统计推断得到模型参数来还原这个结构。

一个典型例子是汉考特（Handcock）等人［53］提出的隐含位置聚类模型（Latent Position Cluster Model），该模型考虑了网络连通性及用户节点在属性和聚集特性上所表现的“同质性”［54-57］等3个结构特征，并为每个用户分配一个在多维欧式空间中的“社会定位”（Social Position）［58］。模型通过假定相似的用户通常会聚集在同一个“社会定位”中，而相异的用户的“社会定位”相距较远，来模拟社交网络中用户交友关系的“同质性”现象。若令任意一对具有“社会定位”zi和zj的用户i和j之间存在链路的概率是相互独立的，那么可以由此得到：

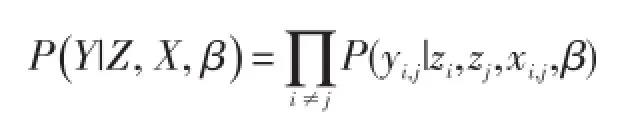
其中yi，j表示用户i与用户 j之间是否存在连接，X=｛xi，j｝表示用户i与用户 j之间的结构特征向量，β代表所有待估参数。若假设yi，j依赖于其节点对之间的欧氏距离，则有：

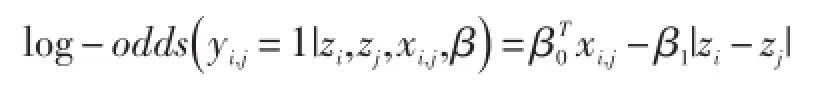
其中log-odds（ A）=log［P（A）/｛1-P（A）｝］。通过将网络连通性表示成任意一对用户间连接的存在性，该式解释了模型中对于网络连通性与用户“社会定位”的欧氏距离和特征向量X之间的回归关系假设。而对于节点聚集现象的描述则是通过假设“社会定位”zi是从有限个均值不同的多元正太分布中抽得的：

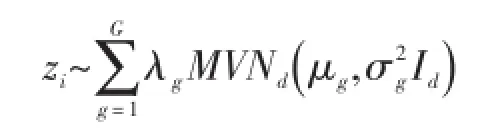
整个网络的联合概率分布可以表示为：

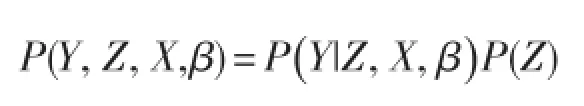
随机生成模型的求解方法通常分为两种，一种经典贝叶斯学派的方法，将β看作参数，然后用极大似然估计法求得待估参数的取值，贝叶斯学派则将β看作随机变量，然后通过MCMC方法得到β的取值。

块模型［59，60］是一类重要的随机生成模型，该类模型常被应用于建模包含社团结构的网络以辅助社团挖掘工作。其中最简单的块模型被称为基础块模型，该模型假设网络中存在一定数目的社团［61］，每个用户节点属于其中的一个社团，且处于不同社团中的用户之间以概率prs建立连边。通过为处在同一个社团内部的节点之间分配较高的连边概率，而社团之间的连边分配较低的连边概率，则可以生成符合社团结构的形式化定义，即社团内部连边密集而社团之间连边稀疏，有似然函数：

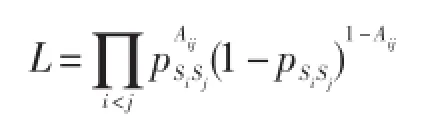
其中Aij代表网络的邻接矩阵中第i行第j列的元素，取值为1表示的节点i和节点j之间存在连边，为0表示不存在连边，Si表示节点i所属的社团编号，令i＜j是为了保证求积范围处于对角矩阵上，避免重复计算。通过极大化似然概率拟合某个包含社团结构的网络，就可以得到连边概率值pSiSj和任意节点所属社团的编号Si。

需要注意的是，一个错误的随机生成模型不但无法准确描述网络的生成过程，反而会造成我们对网络结构的错误认识。用上述块模型拟合美国政治团体网络数据［62］，并将属于同一个社团的节点标记为相同颜色，可以得到如图3（a）中的社团划分结果。可以看出，该划分结果与真实情况不符：众所周知，美国的主要政党是民主党和共和党，因此支持相应政党的网民自然地形成了2个群体，并聚集在本社团内影响力较高的意见领袖周围，进而形成类似于图3（b）中的社团划分结果，这说明基础块模型拟合数据的质量较差，没能有效解释该网络的形成机理。若令图3（b）中较大的节点代表度数较高的用户，而较低的代表度数较小的用户，则通过肉眼观察就可以看出，在同一个社团中的节点其节点度分布范围较广，而非图3（a）中节点度相近的用户属于一个社团，因此通过修改模型，假设每个社团中的节点度服从泊松分布，则可以得到图3（b）中符合真实情况的社团划分。

图3　美国政治选民网络在不同模型中的社团划分结果［62］

3　总结与展望

社交网络结构的研究与分析，是社交网络研究中最早得到重视和探索的领域。本文针对社交网络结构特性和建模研究中的主要问题和研究进展进行了综述，给出了基于真实社交网络的经验数据之上统计属性的描述，包括小世界现象和无标度特性、网络弹性、核与核度、中心性、同配性、社区结构、网络特性与合作行为的关系。这些统计特征不仅包含复杂网络都具有的共性，如小世界现象，也有社交网络所具有的特性，如同配性及其演化。在结构建模部分，我们将现有研究工作分成网络构造模型和随机生成模型来阐述。

社交网络是一种特殊的复杂网络。其特殊性主要体现在它是一种智能化很强的网络，原因是它的基本要素是人。社交网络拓扑结构的形成受人的世界观、生活环境、所处位置、职业环境特别是人的成长环境的影响，导致社交网络的拓扑结构遵循“物以类聚、人以群分”的特点。因此，我们提出应该以图论、博弈论、决策论、规划论、排队论等为主要工具，在以下几个方面对社交网络进行深入研究：

（1）社交网络结构是否服从局部核度最小原则。类似于构成人的神经网络的连接符合核度最小原则一样，是否社交网络的连接也服从局部核度最小原则？核度描述了网络的连通程度，也是衡量构成网络节点重要程度的指标。我们提出猜想，在社交网络中，社区内部服从核度最小原则，这一猜想是否成立有待进一步研究；

（2）亏格理论在网络结构上的应用。亏格是代数拓扑学中的一个基本概念。亏格刻画了代数结构中的连通性。如果找到一种基于图论方法表示的网络结构与代数结构之间的转换，使用较为成熟的亏格理论对网络结构进行评价，这样将能够解决大量的社交网络中的基本问题；

（3）社区的定义问题。目前，各种定性的社区定义，使得不同的社区发现方法层出不穷，但这些社区发现算法往往不能被很好的应用。统一的社区定义不仅可以规范问题，而且可以基于此产生一系列的社区评价基准数据集和社区评价方法；

（4）对社交网络中个体（即作为基本要素的人）的优化决策研究。个体在社交网络中既有合作又有竞争，因此社交网络中个体的优化决策问题，往往被描述成运筹学中的优化问题。无论是以全局属性作为优化的目标函数、还是以个体属性作为优化的目标函数，往往总是假设个体是理性的、智慧的。但是这种假设并不符合实际。量化个体理性的程度将是一个重要且较为困难的问题。

社交网络中问题的复杂性来源于人的社会性及人与人交往的复杂性。社交网络结构理论研究对认识网络结构组织规律、个体行为规律、社会演化机理、信息安全均有着重要的意义。社交网络中的问题往往涉及到多个领域，单纯凭借一种理论来解释社交网络中的现象是不够的。多学科的交叉和融合是解决复杂的社交网络结构特性分析和建模问题的必然途径。

1 Milgram S.The small world problem.Psychology Today，1967，2（1）：60-67.

2 Watts D J，Strogatz S H.Collective dynamics of'smallworld'networks.Nature，1998，393：440-442.

3 MisloveA，Marcon M，Gummadi K P et al.Measurement and analysis of online social networks.Proceedings of the 7thACM SIGCOMM conference on internet measurement，2007，29-42.

4 Kleinberg J.The small-world phenomenon and decentralized search.SiAM News，2004，37（3）：1-2.

5 BarabasiAlbert-Laszlo，Albert Reka.Emergence of scaling in random networks.Science，1999，286（5439）：509-512.

6 Barabási B YAL，Bonabeau E.Scale-free.ScientificAmerican，2003.

7 Jeong H，Tombor B，Albert R et al.The large-scale organization of metabolic networks.Nature，2000，407（6804）：651-654.

8 Liu G，Ji C.Scalability of network-failure resilience：analysis using multi-layer probabilistic graphical models.Networking，IEEE/ ACM Transactions on，2009，17（1）：319-331.

9 Albert R，Jeong H，BarabásiAL.Attack and error tolerance of complex networks.Nature，2000，406（6794）：378-382.

10 Borgatti S P，Everett M G.Agraph-theoretic perspective on centrality.Social Networks，2006，28（4）：466-484.

11 Wehmuth K，ZivianiA.Distributed algorithm to locate critical nodes to network robustness based on spectral analysis.arXiv preprint arXiv：1101.5019，2011.

12 KermarrecAM，Le Merrer E，Sericola B et al.Second order cen-trality：Distributed assessment of nodes criticity in complex networks.Computer Communications，2011，34（5）：619-628.

13 Grubesic T H，MurrayAT.Vital nodes，interconnected infrastructures，and the geographies of network survivability.Annals of theAssociation ofAmerican Geographers，2006，96（1）：64-83.

14许进.系统的核与核度理论（VII）——子核与核度的计算.系统工程学报，1999，（3）.

15 Wu Y L，Yang Y，Jiang F et al.Coritivity-based influence maximization in social networks.PhysicaA：Statistical Mechanics and itsApplications，2014，467-480.

16 Bhawalkar K，Kleinberg J，Lewi K et al.Preventing unraveling in social networks：the anchored k-core problem//Automata，Languages，and Programming.Springer Berlin Heidelberg，2012，440-451.

17 Newman M E J.Ameasure of betweenness centrality based on random walks.Social Networks，2005，27（1）：39-54.

18 Kitsak M，Gallos L K，Havlin S et al.Identification of influential spreaders in complex networks.Nature Physics，2010，6（11）：888-893.

19 Borge-Holthoefer J，Moreno Y.Absence of influential spreaders in rumor dynamics.Physical Review E，2012，85（2）：026116.

20 Holme P，Kim B J，Yoon C N et al.Attack vulnerability of complex networks.Physical Review E，2002，65（5）：056109.

21方滨兴，许进，李建华等.在线社交网络分析.北京：电子工业出版社，2014.

22 Newman M E J.Assortative mixing in networks.Physical Review Letters，2002，89（20）：208701.

23 Hu H B，Wang X F.Disassortative mixing in online social networks.EPL（Europhysics Letters），2009，86（1）：18003.

24 Gong N Z，Xu W，Huang L et al.Evolution of social-attribute networks：measurements，modeling，and implications using google+//Proceedings of the 2012ACM conference on Internet measurement conference.ACM，2012，131-144.

25 Bollen J，Gonçalves B，Ruan G et al.Happiness is assortative in online social networks.Artificial life，2011，17（3）：237-251.

26 Benevenuto F，Rodrigues T，Almeida V et al.Detecting spammers and content promoters in online video social networks//Proceedings of the 32nd internationalACM SIGIR conference on Research and development in information retrieval.ACM，2009，620-627.

27 Palla G，Derenyi I，Farkas I et al.Uncovering the overlapping community structure of complex networks in nature and society.Nature，2005，435（7043）：814-818.

28Ahn YY，Bagrow J P，Lehmann S.Link communities reveal multiscale complexity in networks.Nature，2010，466（7307）：761-764.

29 Newman M.Modularity and community structure in networks.Proceedings of the NationalAcademy of Sciences，2006，103（23）：8577-8582.

30 Yang J，Leskovec J.Defining and evaluating network communities based on ground-truth.In proceedings of theACM SIGKDD workshop on mining data semantics.ACM，2012.

31 Radicchi F，Castellano C，Cecconi F et al.Defining and identifying communities in networks.Proceedings of the NationalAcademy of Sciences，2004，101（9）：2658-2663.

32 Kumpula J M，Kivela M，Kaski K et al.Sequential algorithm for fast clique percolation.Physical Review E，2008，78（0261092）.

33 Evans T，Lambiotte R.Line graphs，link partitions，and overlapping communities.Physical Review E，2009，80（1）：016105.

34Agarwal G，Kempe D.Modularity-maximizing graph communities via mathematical programming.European Physical Journal B，2008，66（3）：409-418.

35 LancichinettiA，Fortunato S，Kertesz J et al.Detecting the overlapping and hierarchical community structure in complex networks.New Journal of Physics，2009，11（033015）.

36Airoldi E M，Blei D M，Fienberg S E et al.Mixed membership stochastic blockmodels.The Journal of Machine Learning Research，2008，9：1981-2014.

37 Yang J，Leskovec J.Community-affiliation graph model for overlapping network community detection，in data mining（ICDM），2012 IEEE 12th international conference on.IEEE，2012，1170-1175.

38 Fortunato S，Barthelemy M.Resolution limit in community detection.Proceedings of the NationalAcademy of Sciences，2007，104（1）：36-41.

39Apicella C L，Marlowe F W，Fowler J H et al.Social networks and cooperation in hunter-gatherers.Nature，2012，481（7382）：497-501.

40 Erdds P R，WIA.On random graphs I.Publ.Math.Debrecen，1959，6：290-297.

41Amaral LAN，ScalaA，Barthelemy M et al.Classes of smallworld networks.Proceedings of the national academy of sciences，2000，97（21）：11149-11152.

42 Newman M E J.The structure of scientific collaboration networks.Proceedings of the NationalAcademy of Sciences，2001，98（2）：404-409.

43Albert R，BarabásiAL.Statistical mechanics of complex networks.Reviews of Modern Physics，2002，74（1）：47.

44 Sen P，Dasgupta S，ChatterjeeAet al.Small-world properties of the Indian railway network.Physical Review E，2003，67（3）：036106.

45 Kleinberg J M，Kumar R，Raghavan P et al.The web as a graph：measurements，models，and methods//Computing and combinatorics.Springer Berlin Heidelberg，1999：1-17.

46 Kumar R，Raghavan P，Rajagopalan S et al.Extracting large-scale knowledge bases from the Web//VLDB.1999，1-99：639-650.

47 FlaxmanAD，FriezeAM，Vera J.Ageometric preferential attachment model of networks II.Internet Mathematics，2007，4（1）：87-111.

48 Leskovec J，Kleinberg J，Faloutsos C.Graphs over time：densification laws，shrinking diameters and possible explanations//Proceedings of the eleventhACM SIGKDD international conference on Knowledge discovery in data mining.ACM，2005：177-187.

49 Leskovec J，Kleinberg J，Faloutsos C.Graph evolution：Densification and shrinking diameters.ACM Transactions on Knowledge Discovery from Data（TKDD），2007，1（1）：2.

50 Leskovec J，Chakrabarti D，Kleinberg J et al.Kronecker graphs：An approach to modeling networks.The Journal of Machine Learning Research，2010，11：985-1042.

51 Kumar R，Novak J，TomkinsA.Structure and evolution of online social networks//Proceedings of the 12thACM SIGKDD international conference on knowledge discovery and data mining.ACM，2006：611-617.

52 Leskovec J，Backstrom L，Kumar R et al.Microscopic evolution of social networks//Proceedings of the 14thACM SIGKDD international conference on knowledge discovery and data mining. ACM，2008：462-470.

53 Handcock M S，RafteryAE，Tantrum J M.Model-based clustering for social networks.Journal of the Royal Statistical Society：SeriesA（Statistics in Society），2007，170（2）：301-354.

54 Wasserman S.Social network analysis：Methods and applications. Cambridge：Cambridge university press，1994.

55 Lazarsfeld P F，Merton R K.Friendship as a social process：Asubstantive and methodological analysis.Freedom and control in modern society，1954，18（1）：18-66.

56 Freeman L C.Some antecedents of social network analysis.Connections，1996，19（1）：39-42.

57 McPherson M，Smith-Lovin L，Cook J M.Birds of a feather：Homophily in social networks.Annual Review of Sociology，2001：415-444.

58 Hoff P D，RafteryAE，Handcock M S.Latent space approaches to social network analysis.Journal of theAmerican StatisticalAssociation，2002，97（460）：1090-1098.

59 Breiger R L，Boorman SA，Arabie P.An algorithm for clustering relational data with applications to social network analysis and comparison with multidimensional scaling.Journal of Mathemati-cal Psychology，1975，12（3）：328-383.

60 Holland PW，Laskey K B，Leinhardt S.Stochastic blockmodels：First steps.Social Networks，1983，5（2）：109-137.

61 Newman M E J.Communities，modules and large-scale structure in networks.Nature Physics，2012，8（1）：25-31.

62 Karrer B，Newman M E J.Stochastic blockmodels and community structure in networks.Physical Review E，2011，83（1）：016107.

The study of networks in form of graph theory is one of the fundamental ontologies to understand the nature behind networks.The term structure is named by using the same term in the domain of graph theory，which implies vertices，edges，and the connection between them.In order to comprehend the mechanism of social network formation and the laws behind the social behavior，we should always study the structure of social network in prior.By studying network structure，we can also gain deeper insights on other specific researching fields on social network，such as information retrieval，influence maximization，user behavior analysis，recommendation，etc.

The topic of research on social network structure consists of two main parts：structural feature analysis and network structure modelling.Analyzing the features of social network is a necessary preparation for modelling social network structure.In this article，we give a comprehensive review of structural features and properties of social network first.Then，two types of models about social network structure are introduced.In the part of feature analysis of social network，we enumerate major features of social network，such as“small world”phenomenon，scale free property，centrality，network resilience，assortative mixing，and community structure.Then，we introduce one excellent work about the evolution of social network structure.In this work，it is confirmed that due to the universal cooperation，the structural characteristics in modern social network and online social network have long been existed in the ancient times.In the part of modelling social network structure，we firstly introduce the type of basic generative model.These models originated from the ER random networks model and developed into a large family of network models featured by“small-world”phenomenon and scale free properties.By simulating human behavior in online social networks，several models are proposed and they are capa-ble of recovering structural features of the observed network data in different aspects.Secondly，the type of stochastic generative models are introduced，these kinds of models can be used to postulate complex latent structures responsible for a set of network observations，and this makes it possible to recover this structure by statistical inference.It is also emphasized that in order to fit the data well，one need to guard against that the proposed model is realistic enough.

Future research directions are discussed in the last section.One important direction is to prove the coritivity conjecture. The coritivity conjecture says that community structures are formed by minimizing the coritivity of its subgraph and the feature graph of social network，in which by replacing all communities with equal number of nodes，the derived network also follows the principle of coritivity minimization.The verification and proof of this conjecture will solve some vital problems in the domain of social network，such as understanding mechanisms of structural formation.Other important future directions include introducing genus from algebraic structure，defining community structures，quantification of individual rationality.We hope this paper will provide inspirations for researchers and an insight for the government's network security strategy in the view of network science.

许进 北京大学信息科学技术学院教授，博士生导师。1993年获西安交通大学管理工程专业工学博士；1995年获北京理工大学数学系理学博士。中国电子学会电路与系统学会副主任；中国电子学会图论与系统优化专业委员会理事长。主要研究方向为社交网络、生物计算、图论与组合优化等。主持承担了多项国家级重要科研项目和国际合作项目。2013年作为第一完成人获国家自然科学奖二等奖。E-mail：jxu@pku.edu.cn

Xu Jin，currently a Professor of Electronic Engineering and Computer Science in Peking University.He is committee member of Circuits and Systems Society and Councilor of Professional Committee of Graph Theory and System Optimization in Chinese Institute of Electronics.He received his PhD degree in Management Engineering in 1993 from Xi'an Jiaotong University and PhD degree in Mathematics in 1995 from Beijing Institute of Technology of China.His current research interests include social network analysis，bio-computing and graph theory and combinational optimization.He has published over 200 research papers in reputed journals and conferences and conducted over 10 research projects including National 863 Project of China，National 973 Project of China，Key Project of National Natural Science Foundation of China，etc.Jin Xu got 2rd National Prize for Natural Sciences in 2013.E-mail：jxu@pku.edu.cn

金舒原 女，中科院计算技术所研究员。2006年获香港理工大学网络安全方向博士学位。主要研究方向为网络安全、社交网络等。主持承担了国家自然科学基金青年科学基金项目、国家863项目、发改委安全专项等多项研究工作。在国内外重要学术期刊上发表学术论文40余篇。

E-mail：jinshuyuan@ict.ac.cn

Jin Shuyuan，female，currently a Professor in Institute of Computing Technology，Chinese Academy of Sciences.She received her PhD degree in Network Security in 2006 from Department of Computing，HongKong Polytechnic University.Her current research interests include network security and social network analysis.She has published over 40 research papers in reputed journals and conferences.Her recent research activities are generously supported by the National Natural Science Foundation of China and the National High Technology Research and Development Program of China.E-mail：jinshuyuan@ict.ac.cn

Social Network Structure Feature Analysis and Its Modelling

Xu Jin1Yang Yang1Jiang Fei1Jin Shuyuan2
（1 School of Electronics Engineering and Computer Science，Peking University，Beijing 100871，China；2 Institute of Computing Technology，ChineseAcademy of Sciences，Beijing 100190，China）

With the rapid growth of social network services，social network has been an important scientific research area.Researches on network structure，information diffusion and retrieval，user behavior analysis，community detection on social network have made great progress.In this article，domestic and international researches progress on social network structure is reviewed.We focus on two main issues of this research direction，namely，feature analysis and structural modelling of social networks.In the end，we summarize the existing problems and give some possible solutions for enlightening the researchers on this area and for providing guidance for government's decision making.

social network，network structure，feature of network structure，modeling on network

国家重点基础研究发展计划（“973”）项目（2013CB329600）

**通讯作者

修改稿收到日期：2015年2月4日