基于连续介质的土质边坡稳定性分析
2015-10-31王朝虎
王朝虎
(中铁十一局五公司 重庆 沙坪坝 400000)
基于连续介质的土质边坡稳定性分析
王朝虎
(中铁十一局五公司重庆沙坪坝400000)
本文采用基于连续介质的差分软件Flac3d,对土质边坡的典型的破坏形式、破坏类型及破坏的特征点进行分析。得出:土质边坡破坏的主要特征是在坡脚处发生位移突变,坡体的塑性区也基本贯通,及计算不收敛等情况。一般情况下土质边坡会首先在坡体角处产生较大幅度的变位,并且变位的区域从坡脚处不断向坡顶发展,同时还会在坡脚处产生塑性应变,也逐渐向坡顶发育,但是其发育的速度小于变位区域增大的速度,最后塑性区贯通,坡脚处位移产生急剧变位后,坡体失稳。接着随着坡体变形的持续增加,会导致最终的计算不收敛。
Flac3d;土质边坡;失稳判据;理论分析
1 引言
滑坡作为一种常见地质灾害,具有长期性、突发性和具有较大的破坏性,给人们的生命财产安全造成了极大的威胁,因此如何提前预测、警告、预防滑坡的发生具有较大的经济和社会意义[1~5]。目前关于如何判断滑坡失稳判断依据还众说纷纭,目前主流的主要有以下三种判断依据:①赵尚毅、郑颖人、张玉芳等[6]通过大量研究提出以数值收敛作为模型的收敛性作为边坡失稳的判据;②宋二祥(1997),刘金龙等提出以坡脚的位移突变作为边坡失稳判据;③奕茂田、武亚军、年廷凯等(2003)提出以坡体塑性区的贯通作为边坡失稳的判据。还有一些通过本构模型和新型判断理论来对边坡失稳的判据进行探讨和研究。
但是以上的研究均是集中于某一种失稳判据的研究,而在实际的坡体失稳中往往是一种或几种工作作用的结果,单独只对一种进行讨论往往使得对坡体判据的讨论缺乏全面性和综合性。基于此,本文以土质边坡的破坏为研究对象,通过对目前主流坡体失稳判据的理论的深入研究,并结合目前土质边坡失稳判据的主要形式进行分析(坡脚位移突变、塑性区贯通、计算不收敛),分析三者之间的相互关系,探讨这三种失稳形式在土质滑坡中发生的时空顺序和条件,克服传统的基于单一的判断依据,提高判据的精准性,为土质边坡的滑坡治理提供参考。
2 Flac3d基本原理
Flac3d是由美国Itasca公司开发的,基于三维快速拉格朗日差分法的岩土方面专用软件,共有10种材料模型:
(1)开挖模型null;
(2)3个弹性模型(各项同性、横观各项同性和正交各项同性弹性模型);
(3)6个塑性模型(Drucker-Prager模型、Mohr-coulomb模型、应变硬化/软化模型、遍布节理模型、双线性应变软化/软化遍布节理模型和修正的cam粘土模型。
Flac3d是在二维的有限差分程序Flac2d的扩展,能够进行土质、岩石和其他材料的三维结构受力特性模拟和塑性流动分析,具有以下几个优点:
(1)对模拟塑性破坏和塑性流动采用的是“混合离散元法”。这种方法比有限元法中通常采用的“离散集成法”更为准确合理。
(2)即使模拟系统的静态的,仍采用动态运动方程,这使得Flac3d在模拟物理上的不稳定过程不存在数值上的障碍。
(3)采用一个“显式解”方案。因此,显式解方案对非线性的应力-应变关系的求解所花费的时间,几乎与线性本构关系相同,而隐式求解方案将会花费更多的时间求解非线性问题。而且,它没有必要存储矩阵刚度,这就意味着采用中等容量的内存可以求解更多的单元结构;模拟大变形问题几乎并不比小变形问题多消耗更多的计算时间,因为没有任何刚度矩阵要被修改。
3 基本模型参数
如图1所示为边坡的模型尺寸,此边坡模型长50m,坡顶长20m,前后高差15m。
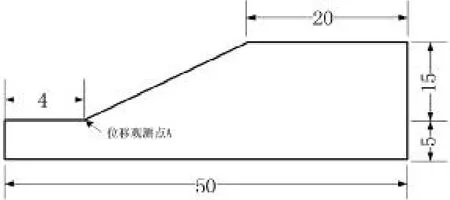
图1 边坡的模型尺寸(单位:m)
如表1所示为土体参数。

表1 土体参数
4 模拟分析
如图2-a、图2-b所示,为初始模型网格图和经过1200步计算后的网格图。从上述计算前后的对比可以看出,经过1200步的计算后,网格产生的较大的变形,在坡脚处产生了较大的变位,同时在斜坡的临坡面形成一个明显的弧形的滑动带,进而形成一个明显的滑坡体。在坡脚和滑动带处由于坡体变形的增大,导致网格变形较为严重。坡体最终发生失稳,而形成滑坡。
图3~4为计算200步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。从图3、图4可以看出,在边坡刚刚有失稳的趋势时,坡体的坡脚处是整个坡面附近产生变位最大的地方,是整个坡面位移突变的地方;同时,坡体的塑性区也仅仅在坡脚处形成,坡体整体位移相对不大,坡体整体还处于亚安全的状态。

图2 计算前后边坡模型网格变化图

图3 200步时的模型位移云图和A的位移曲线

图4 200步时的模型塑性应变云图和A的位移曲线
图5~6为计算400步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。从图5~6可以看出,随着计算的进行,坡脚处的位移持续增大,从A点的位移变化曲线还可以看出坡脚处的变位速率在增大,且坡脚破坏的区域也在同步增大,但是坡顶处为位移相对变化不大;边坡的塑性应变还是集中在坡脚处,略微向上扩展,但扩展范围不大。以上说明边坡在由失稳的趋势时,会首先在坡脚处产生剧烈的变位,且变位的区域在坡脚处不断扩大,塑性区随着坡脚处变位的增大而缓慢增大,且增长速度赶不上坡体变位区域扩大的速度。

图5 400步时的模型位移云图和A的位移曲线
图7~8为计算600步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。从图7~8可以看出,当坡体模型计算到600步时,整个坡体临空面的位移持续增大,但还是以坡脚处的位移为最大,同时,坡体的塑性应变带(坡体的滑动带)从坡脚处开始形成并快速的向坡顶发展。边坡处于半失稳区,同时由于坡脚处的最大位移已达到9cm,坡体有先破坏的趋势。

图6 400步时的模型塑性应变云图和A的位移曲线

图7 600步时的模型位移云图和A的位移曲线
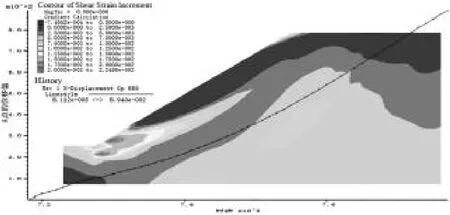
图8 600步时的模型塑性应变云图和A的位移曲线
图9~10为计算800步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。从图9~10可以看出,随着坡体位移的不断持续增大,坡体的滑体区域愈加明显,滑动带也不断向坡顶发展,当运行到800步时,坡体的塑性区已贯通80%,坡体随时可能失稳。

图9 800步时的模型位移云图和A的位移曲线
图11~12为计算1000步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。从图11~12可以看出,坡体的滑坡体区域基本固定,但位移不断增大,同时土体的塑性应变(坡体的滑动带)已基本贯通,坡脚处的位移最大值也达到了30cm,坡脚处已失稳。整个坡体正在快速失稳。
图13~14为计算1200步时坡体模型的位移云图、塑性应变云图及A点的位移变化曲线。当运算到1200步时,坡体的塑性区已完全贯通,坡脚处的最大位移也迅速升到32cm。此时说明坡体已经完全失稳。此后,接着计算出现坡体位移持续增大,滑带的塑性应变也不断增大,模型计算已经不能自我平衡收敛。可以看出坡体在有失稳趋势和失稳发育的过程中,坡脚处会首先生成较大变位且变位区域不断扩大(从坡脚到坡顶),坡体的塑性应变带也从坡脚处开始形成,并不断向坡顶发育,并最终贯通,导致坡体失稳,坡体失稳后,计算无法达到自我平衡而无法收敛。

图10 800步时的模型塑性应变云图和A的位移曲线

图11 1000步时的模型位移云图和A的位移曲线
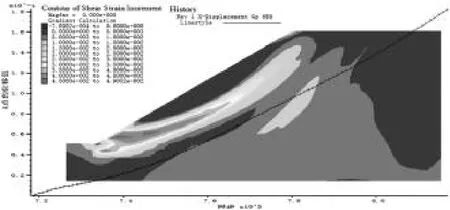
图12 1000步时的模型塑性应变云图和A的位移曲线

图13 1200步时的模型位移云图和A的位移曲线
5 结论
(1)边坡在在由失稳趋势和正在失稳的过程中,会在坡脚处产生较大且持续的变位,同时由于塑性应变所产生的滑动带也在坡脚处形成,但是其在形成速度和产生区域的均小于坡体变位的区域和速度。说明坡体在失稳过过程中会先产生坡脚处的位移持续变化后再形成滑动带。
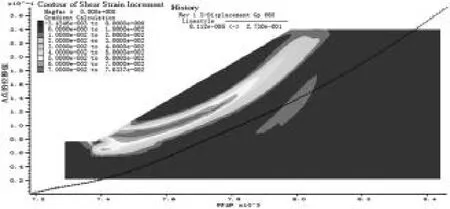
图14 1000步时的模型塑性应变云图和A的位移曲线
(2)在坡体的塑性区贯通时,坡体产生塑性滑动,此时坡脚处会产生距离的位移突变,进而引起整个坡体的失稳变形。
(3)通过前述分析,整个坡体的变形失稳顺序为:坡脚处持续变形且变形区域不断向坡顶发展-坡体的滑动在坡脚处形成,并随着坡体变位的增加而逐渐向坡顶发育,并最终贯通-坡体塑性应变贯通,坡体失稳,坡体产生持续的变形,模型无法自我平衡而导致收敛失败。
[1]张先良.边坡渐进破坏及稳定性分析[D].中南大学,2008.
[2]卫强.公路路基高边坡整体稳定性分析研究[D].重庆交通大学,2010.
[3]赵智超.山区高速公路边坡稳定性分析[D].河北工业大学,2011.
[4]李月峰.高填土边坡稳定性分析[D].中南林业科技大学,2012.
[5]张年胜.红砂岩边坡稳定性分析及治理研究[D].长沙理工大学,2012.
[6]赵尚毅,郑颖人,时卫民,王敬林.用有限单元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,34(3):343~346.
TU457
A
1673-0038(2015)21-0170-03
2015-5-9
王朝虎(1981-),男,工程师,本科,从事工作方向为工程管理。
