时移双曲方程速度分析原理及应用
2015-10-31商乃德
商乃德
(中国海洋石油能源发展股份有限公司,北京 100027)
时移双曲方程速度分析原理及应用
商乃德
(中国海洋石油能源发展股份有限公司,北京 100027)
针对时移双曲线NMO方程的非椭圆特性,研究时移参数和非椭圆参数之间的关系,引入了局部坐标系中能描述反射双曲线形状的两个约束参数,推导出相关计算公式。建立了各向异性速度分析处理流程,解决了远炮检距动校道集无法校平的问题,提高了叠前时间偏移的成像精度。通过不同实例证实了该方法能够有效解决远炮检距情况下反射波准确归位的问题。
垂向对称轴横向各向同性(VTI)介质 时移双曲线 叠前时间偏移 各向异性速度分析
在地层为各向同性水平层状假设且小排列情况下,地震反射波双程旅行时-炮检距的关系可用双曲时差方程表示。实际地层或是在每一层内部各方向(水平方向与垂直方向)的速度不同,或是在每一层中各方向的速度相同,但是在不同层界面之间存在地震射线弯曲现象(垂直对称轴的横向各向同性(VTI)介质),上述情况导致中、远炮检距反射时距曲线偏离双曲形状,这种层内各向异性和VTI介质各向异性的地震信号效应是不可分辨的。由于远炮检距、陡倾角以及地下各向异性情况无法满足地层为各向同性水平层状、小排列的假设条件,基于二阶双曲时差方程[1,2,5-9]的时间域成像方法忽视了介质速度垂向非均匀性和层内各向异性现象,导致远炮检距数据,特别是陡倾角数据不能聚焦成像。在考虑各向异性地震波成像时,叠前时间偏移无疑是目前最实用的地震波成像技术之一,获得各向异性速度场就成为成像的关键。对基于时移双曲方程的各向异性速度分析方法原理、影响因素、实现过程进行分析,并把该方法应用于叠前时间偏移处理中,解决了远炮检距反射波准确归位问题,提高了构造成像精度,并能为叠前反演提供高质量的CRP道集。
1 方法原理
反射波曲线的非双曲线特征,通常是由于波在各向同性层状介质中射线弯曲和在各向异性均匀介质中传播造成的,为了使各向异性速度场计算实用化,人们经过长期研究对各向异性模型进行了简化(垂直对称轴的横向各向同性(VTI)介质)。目前,叠前时间偏移获得各向异性速度场的方法主要有两种:一种是基于均匀VTI介质模型的常规四阶NMO动校正方法,把这种方法推广到层状介质模型,并最终应用到非均匀VTI介质中[1];另一种方法是基于各向同性层状介质模型,应用时移双曲线动校正方法[2],把该方法推广到均匀VTI介质,并最终等效应用到非均匀VTI介质中。
1.1均匀VTI介质的时差方程
通过对各向异性介质进行简化,Alkhalifah等[1]证明了包含介质不同层界面之间存在地震射线弯曲现象和层内各向异性两种效应的非椭圆率参数(η)是所需要的第二个动校参数,该方法中时间域处理只依赖于两个参数:vnmo和η,若vnmo代表水平反射层近炮检距反射曲线,非椭圆率参数η控制非双曲线形状,由此得到增加了NMO方程渐近线特征的均匀VTI介质的旅行时-炮检距关系,可用四阶泰勒级数展开表示为:
(1)
式中:vnmo为动校正速度,m/s;η为等效非椭圆率;x为炮检距,m;t0为零炮检距旅行时,s。
对于非均匀VTI介质来说,vnmo和η是等效值。
1.2时移双曲线NMO方程的非椭圆特性
对于各向同性层状介质来说,通常认为时移双曲线NMO方程是最通用和实用的动校正方法[3],即

(2)
τ0=s-1t0
τs=(s-1)τ0
(3)
无量纲的时移参数s控制了NMO曲线的远炮检距特征;根据时移双曲线动校正方法同样可以建立s和η之间的关系。
相对于均匀VTI介质来说,层状VTI介质的动校参数vnmo和η是等效值[10]。在各向同性层状介质中,等效η值能缩写成四阶项形式[4],即
(4)
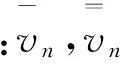
对于VTI介质来说,为了保持式(4)的形式,各向异性速度v可用NMO速度与η的一种组合表示为
v4=v4(1+8η)
(5)

(6)
对于层状介质来说,时移双曲线方程的等效参数s通过四阶与二阶平均速度的比率给出[3],按照层状介质公式(4)和各向异性VTI介质公式(6)相似的特点,四阶各向异性速度的平均可表示为

(7)
式(7)反映了NMO时移双曲方程式(2)~式(3)具有VTI介质的特点,时移项作为等效各向异性参数参与其中,把式(7)代入式(2)、式(3)得到包含项的非椭圆时移双曲线方程

(8)
式中:v为Dix二阶项速度;η为等效非椭圆率;x为炮检距;t0为零炮检距旅行时。
式(8)由Sillqi等[2]通过在模型中引入VTI介质,因此修改了层状介质的动校正方程[3],并证明了包含各向异性地层的垂向非均匀介质特征造成射线弯曲及各向异性引起的远炮检距效应。
为了使用静时移方法引入两个参数(图1),即

(9)
dtn=tx=xmax-tx=0
(10)
式中:τ0为局部双曲坐标系中的零炮检距时间;dtn为最大炮检距处的动校正量。
把式(9)和式(10)代入式(8)得

(11)
由式(11)可以看出动校正不再依赖于t0,把动校正直接获取(v,η)的方式转变成求取(dtn,τ0)的方式,通过对dtn和τ0的高密度双谱分析计算v和η值。
2 影响所有炮检距的动校参数
如果在局部坐标系(反射波曲线为双曲线)中描述时移双曲线动校正,那么,在这种坐标系中可由最大炮检距处的动校正dtn和零炮检距旅行时τ0(图1)两个参数约束反射双曲线形状。

图1 非椭圆时移双曲动校正中动校参数dtn和τ0的关系
如果dtn与双曲动校正无关,那么,只有当反射双曲线是非双曲线形状时,τ0与t0才有差异。图2显示了动校参数dtn和τ0的双扫描结果[5],由图中可以看出dtn:可以有效地约束校正结果;τ0控制了同相轴拉平处理的细微变化。τ0扫描影响所有炮检距,振幅最大出现在中间位置,由于动校正和(dtn,τ0)两者都是用时间值表示的,因此,时移扫描方法可代替各向异性动校正分析方法,这是该方法的第一个优点。

图2 不同(dtn,τ0)对的动校正
该方法的第二个优点是可进行静时差校正,由静时差校正代替动校正大幅度减少了速度分析所花费的时间,通过避免远炮检距拉伸提高了谱的质量。通过采用这种动校正参数化技术,可把常规速度谱扩展到三维分析体(t0,dtn,τ0)。
3 实现过程
时移扫描方法具体实现步骤如下:
(1)高密度dtn和τ0场的自动拾取。高密度dtn和τ0场拾取输入的数据体可以是CMP道集数据,也可以是CRP道集数据。为了提高工作效率,可对输入数据按一定的空间采样间隔(骨架)进行处理。为了提高拾取精度,可以对输入的道集数据做一些必要的预处理(例如预滤波、切除及去噪),提高输入道集数据的信噪比和同相轴的横向相干性;应用大时窗的振幅增益使输入数据的纵横向能量均匀,在此基础上,以预先拾取的常规动校正速度为基准定义速度扫描范围和各向异性参数扫描范围以及横向相干性的门槛值,从而得到dtn和τ0的骨架场,然后对拾取的dtn和τ0值分别进行分解,分解成对应的低频分量和高频分量。
(2)对高密度dtn和τ0场的高频分量分别根据地质构造进行平滑。由于干扰、多次波及人为因素造成的不正确数值都会影响dtn和τ0场,因此,要对dtn和τ0的高频分量分别进行基于地质构造的平滑滤波,从而消除高频分量中存在的突变点,使其反映地层的地质变化。
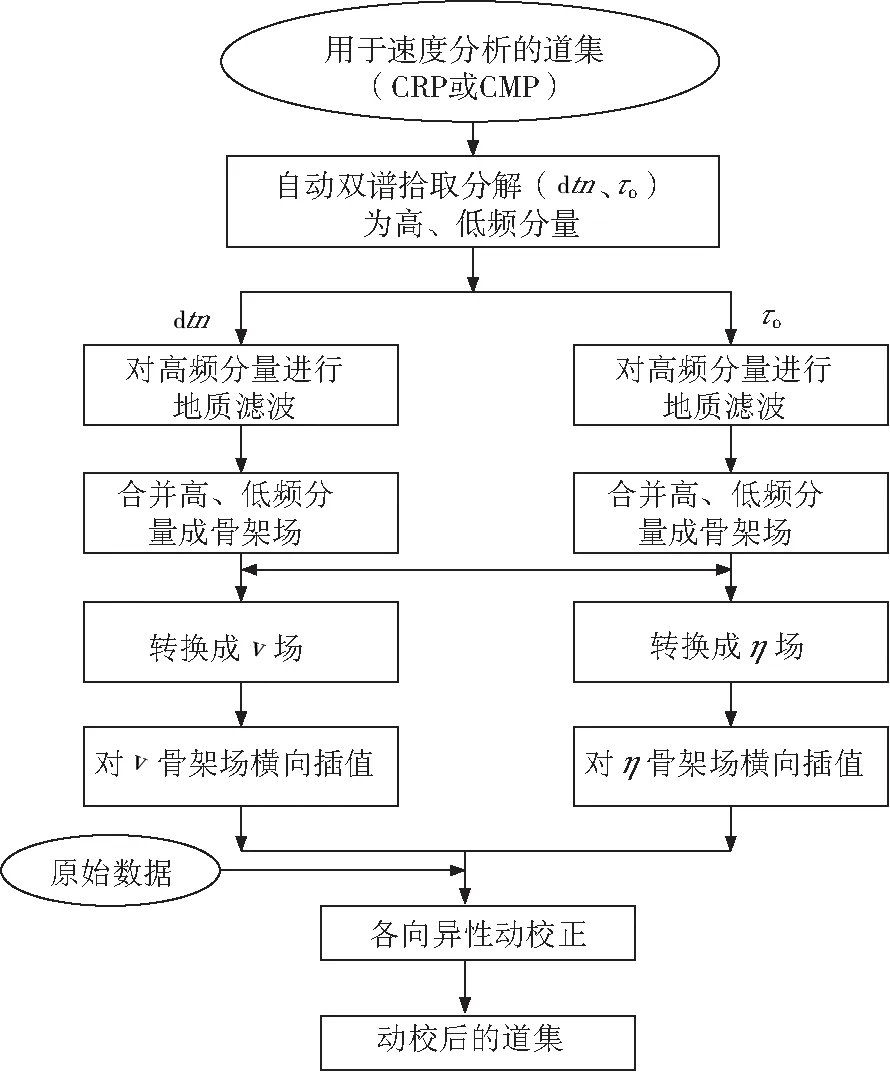
图3 各向异性高密度速度分析处理流程
(3)对高密度dtn和τ0场的低频分量和高频分量进行合并。将经过平滑后的dtn和τ0高频分量与相应的dtn和τ0低频分量合并,从而获得dtn和τ0的骨架场。
(4)把dtn和τ0场转换成v和η场。为了应用v和η进行动校正,需要把dtn和τ0场转换成v和η场,利用dtn和τ0结合可转换成v场,利用τ0转换成η场,从而得到v和η的骨架场。
(5)将v和η的骨架场进行插值。为了得到整个工区每一面元的v和η场,就要对v和η的骨架场进行空间插值,从而使每一面元都有相应的v和η值。各向异性高密度速度分析的流程框图如图3所示。
4 效果分析
通过采用时移方法,高密度双谱速度分析技术以间接方式实现了同时拾取叠加速度和各向异性参数的目的,并且能获取研究区逐点的叠加速度和各向异性参数。与常规速度分析相比,高密度双谱速度分析拾取的速度精度更高,更适合横向速度变化不太剧烈、大倾角地层及远炮检距的地震资料处理。并且高密度双谱速度分析拾取的速度场和各向异性场又能作为输入,进行各向异性叠前时间偏移,减少了人工干预工作量,提高了处理精度。
4.1实例1
葡西三维工区位于大庆长垣西部,深层构造较复杂,中、浅层地层相对平缓,倾角较小,炮检距较大(最大炮检距为5 960 m)。分别采用一步法(同时拾取v场和η场)高密度各向异性自动速度分析和两步法(先拾取v场、其次拾取η场)各向异性速度分析方法,并对两种方法速度分析结果进行对比。从各向同性叠前时间偏移速度分析中发现,该区在1 200~2 000 ms之间远炮检距同相轴校不平(图4)。图5是在图4速度分析的基础上,对η场进行分析得到的结果,从图中可以看出:经过对η场的分析,CRP道集远炮检距同相轴拉平,说明两步法各向异性分析能够解决地层中的各向异性问题。
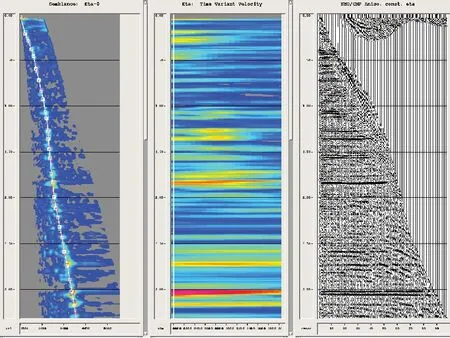
图4 各向同性叠前时间偏移速度谱(左)、η谱(中)及CRP道集(右)
图6是葡西工区inline411线各向同性叠前时间偏移后的一段CRP道集,从图中可以看出:CRP道集存在远炮检距同相轴校不平现象。图7是与图6对应的经一步法和两步法各向异性动校正后CRP道集对比图。从图中可以看出,两种方法都能解决远炮检距同相轴校不平的问题,2 000 ms附近切除区内两种方法校正都很平直,而3 000 ms附近切除区内一步法校正更好。
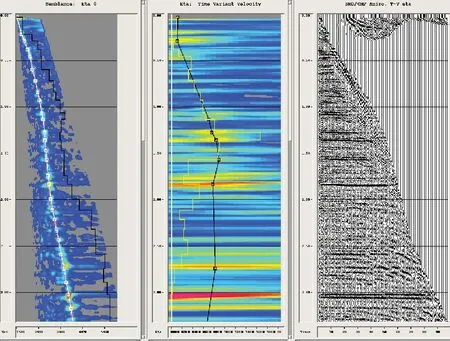
图5 各向异性叠前时间偏移速度谱(左)、η谱(中)及CRP道集(右)

图6 各向同性叠前时间偏移后的CRP道集
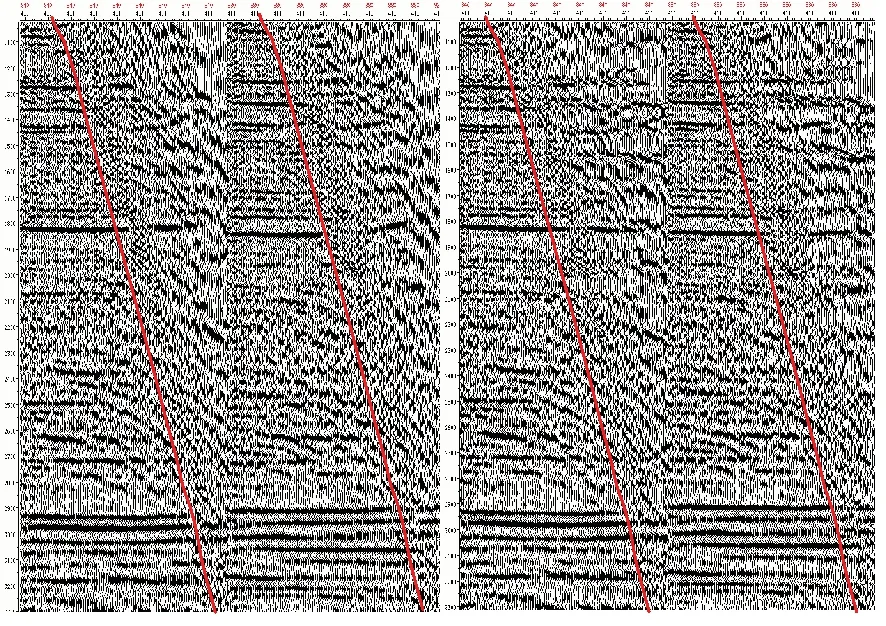
图7 两步法(左)与一步法(右)各向异性叠前时间偏移后的CRP道集
图7是与图8对应的两步法和一步法各向异性叠前时间偏移剖面对比图。从图中看出:一步法叠前时间偏移剖面成像精度(在2 100 ms附近)稍好于两步法叠前时间偏移剖面,同相轴的复波较少,同相轴更加清楚。
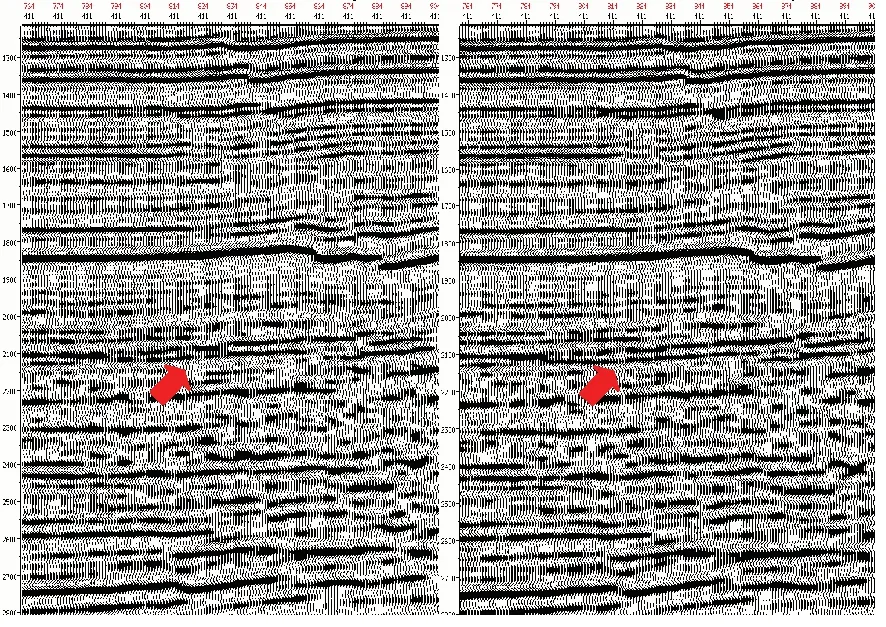
图8 两步法(左)与一步法(右)各向异性叠前时间偏移剖面

图9 各向同性叠前时间偏移后的CRP道集

图10 两步法(左)与一步法(右)各向异性叠前时间偏移后的CRP道集
4.2实例2
图9是葡西工区inline416线一段各向同性速度分析的CRP道集,在1 200~2 000 ms之间出现远炮检距同相轴校不平现象,说明地层存在各向异性问题,仅用各向同性速度分析解决不了各向异性问题。图10是与图9对应的一步法和两步法各向异性动校正后叠前时间偏移CRP道集的对比。从图中可以看出,两种方法都能解决远炮检距同相轴校不平问题,但对于这一段道集而言,一步法动校效果要好于两步法动校效果。图11是与图10对应的一步法和两步法叠前时间偏移剖面。从图中看出,由于一步法叠前时间偏移对远炮检距同相轴拉平程度更好,因此反映在偏移剖面上同相轴(1 400~2 100 ms)清楚,复波现象少,对小断层的刻画更清楚。

图11 两步法(上)与一步法(下)各向异性叠前时间偏移剖面
4.3实例3
一步法各向异性速度分析技术在方正三维工区地震资料处理中进行了应用。该区的特点是:构造复杂,地层倾角大、断裂发育,速度横向变化大,炮检距大(最大炮检距3 937 m,变观处炮检距更大),地震成像对速度精度的要求高。通过应用一步法各向异性自动速度分析后成像效果得到明显改善。图12是各向同性和一步法各向异性速度分析叠前时间偏移的CRP道集对比图,从图中可以看出,各向同性速度分析无法解决远炮检距的各向异性问题,不能将远炮检距同相轴拉平,而经一步法各向异性速度分析的道集远炮检距同相轴拉平。图13是与图12对应的经各向同性速度分析和一步法各向异性速度分析动校后的叠前时间偏移剖面。从图中可以看出,一步法各向异性叠前时间偏移剖面成像精度整体好于各向同性叠前时间偏移剖面,尤其是在构造比较复杂的断裂带附近效果更加明显。

图12 各向同性(左)与一步法各向异性(右)叠前时间偏移后的CRP道集
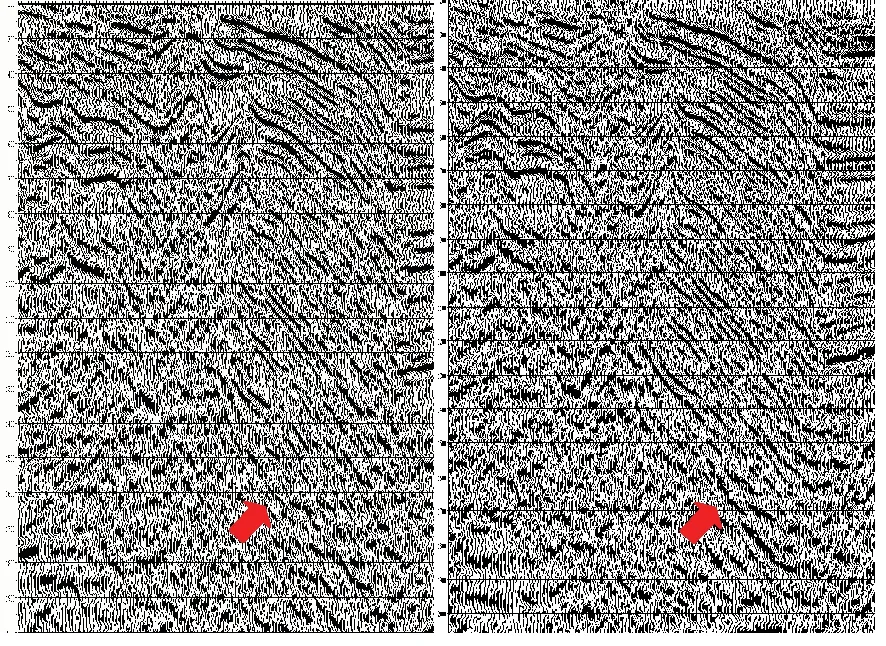
图13 各向同性(左)与一步法各向异性(右)叠前时间偏移剖面
4.4实例4
一步法各向异性自动速度分析技术在松辽盆地太平川高精度三维地震资料处理中同样取得了良好效果。该区断层发育,速度横向有一定变化。图14是太平川工区各向同性和各向异性(一步法)叠前时间偏移动校正道集的对比,从图中可以看出,各向异性叠前时间偏移解决了远炮检距存在的各向异性问题,远炮检距同相轴平直。
图15是与图14对应的各向同性和各向异性叠前时间偏移剖面对比,从图中可以看出,各向异性叠前时间偏移解决了远炮检距成像问题,偏移后断点清楚,与之相比,各向同性叠前时间偏移后断点处绕射波收敛不到位。该实例说明,在速度横向变化较小情况下,各向异性叠前时间偏移对远炮检距或陡倾角的成像精度要优于各向同性叠前时间偏移。

a b
图14 各向同性(a)与一步法各向异性(b)叠前时间偏移后的CRP道集
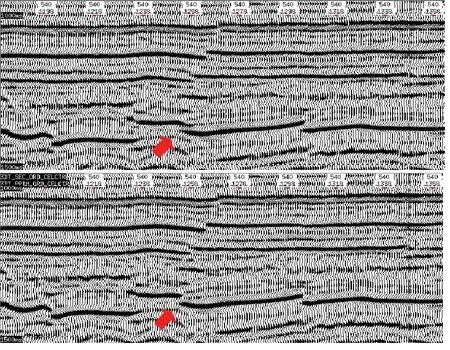
图15 各向同性(上)与一步法各向异性(下)叠前时间偏移剖面
5 结论
不同于四阶泰勒级数逼近方法分两步获得v场(第一步)和η场(第二步),时移双曲线动校正方法通过间接方式同时获得v场和η场,以解决地层的各向异性问题,与各向同性速度分析相比,基于时移双曲方程的各向异性速度分析具有以下优势和特点:
(1)实现了自动逐点速度分析,增加了速度分析的密度,提高了速度分析精度,避免了各向同性速度分析密度低的不足,从而提高了复杂断块的成像精度。
(2)解决了VTI介质的各向异性问题,从而解决了远炮检距动校道集无法校平的问题,提高了叠前时间偏移的成像精度。
(3)由于基于时移双曲方程的各向异性速度分析方法解决了远炮检距动校问题,从而为叠前反演提供了高质量的CRP动校正道集。
[1] Alkhalifah T,Tsvankin I.Velocity analysis for transversely isotropic media[J].Geophysics,1995,60(5):1550-1566.
[2] Siliqi R,Bousquie N.Anelliptic time processing based on a shifted hyperbola approach[J].SEG Expanded Abstracts,2000,19:2245-2248.
[3] Castle R J.A theory of normal moveout[J].Geophysics,1994,59(6):983-999.
[4] Taner M T,Koehler F.Velocity spectra digital computer derivation and applications of velocity functions[J].Geophysics,1969,34(3):859-881.
[5] Siliqi R,Le Meur D.High-density moveout parameter fieldsVandη,PartⅠ:Simultaneous automatic picking[J].Expanded Abstracts of 73rd Annual Internat SEG Mtg,2003:2088-2091.
[6] Le Meur D,Siliqi R.High-density moveout parameter fieldsVandη.PartⅡ:Simultaneous geostatistical filtering[J].Expanded Abstracts of 73rd Annual Internat SEG Mtg,2003:2092-2095.
[7] 肖莉.VTI介质非双曲叠前时间偏移方法对比[J].油气地质与采收率,2010,17(1):57-61.
[8] 潘成磊,张志勇,郭廷超,等.高密度速度分析在YA高精度三维的应用[J].复杂油气藏,2010,3(4):39-42.
[9] 马建波,李绍康,银燕惠,等.东濮凹陷高密度各向异性自动速度分析[J].中国石油勘探,2009,14(6):69-71.
[10] Alkhalifah T.Velocity analysis using nonhyperbolic moveout in transversely isotropic media[J].Geophysics,1997,62(6):1839-1854.
(编辑 韩 枫)
Principle of velocity analysis for time-shifting hyperbolic equation and its application
Shang Naide
(EnergyDevelopmentLtdCo.,CNOOC,Beijing100027,China)
According to nonelliptic features of time-shifting hyperbolic NMO equation,it was carried out the relationship between time-shifting and nonelliptic parameters.By introducing two constrained parameters,which can describe shape of reflected hyperbolic curve in local coordinate system,the correlation calculation formulas were derived.A processing flow of anisotropic velocity analysis was established,which solves the problem of NMO abnormality of far offset data set and improves the imaging accuracy of the previous time offset.Different cases indicated that this method can effectively solve the problem of accurate homing of reflected wave under the condition of far offset.
vertical transverse isotropic (VTI) medium;shift hyperbolic curve;pre-stack time migration;anisotropy velocity analysis
10.16181/j.cnki.fzyqc.2015.04.007
P631.4
A
2015-07-21;改回日期2015-10-17。
商乃德 (1967—),工程师,主要从事勘探方法研究及其市场开发工作。电话:010-84528239,E-mail:shangnd@cnooc.com.cn。
