地铁隧道贯通横向误差分析及工程应用

2015-10-31尹增春

建材与装饰 2015年27期

关键词：方位角导线方向

尹增春

（中交四航局第五工程有限公司　福建　福州　350003）

地铁隧道贯通横向误差分析及工程应用

尹增春

（中交四航局第五工程有限公司福建福州350003）

本文介绍了地铁贯通测量、贯通误差及影响因素，着重对地铁隧道贯通横向误差进行分析，并重点分析了联系测量对贯通横向误差的影响。从地面控制测量、联系测量、地下导线测量三个环节讨论对横向贯通的影响因子，并得出了最终贯通横向误差计算公式。结合工程案例，运用公式对贯通横向误差进行了计算。提出了提高贯通横向误差精度应注意的问题。

贯通测量；横向贯通误差；地面控制测量；联系测量；地下导线测量

1　引言

随着城市化的飞速发展，越来越多的城市已经在建或者规划建设城市轨道交通工程，这其中尤以地铁工程的建设为主要方向。地铁工程主要为地下工程，地下工程由于其特殊性，对测量工作有着更高的要求，而贯通测量作为地铁工程测量中非常重要的一部分，显得尤为重要。

2　贯通测量、贯通误差及其影响因素

贯通测量是地下线型工程（本文主要指地铁）建设中一项非常重要的测量工作。它是为加快施工进度，改善工作条件，在不同地点以两个或两个以上的工作面分段掘进按设计彼此相通的同一隧道时所进行的各种测量工作。其主要任务是确定并给出隧道在空间的位置和方向，以保证所掘进的隧道符合设计要求。

贯通误差包括沿隧道中心线的纵向偏差，水平面内垂直于隧道中心线方向的偏差（贯通横向偏差）和垂直面内的高程偏差。本文主要讨论贯通横向偏差。影响隧道贯通误差的主要因素有地面控制测量、联系测量和地下控制测量，本文以竖井区间隧道为例，从这三方面对地铁贯通横向误差的影响进行一些简要分析。

3　贯通相遇点k在水平重要方向x′（横向）上的误差分析

3.1地面平面控制测量误差引起的k点在x′方向上的误差

在此，地面平面控制测量我们以地铁建设中经常采用的精密导线网为例进行分析。通常，我们在地面两井口近井之间布设闭合导线或附合导线，这时，在进行地面导线的严密平差时，应同时评定出相应的精度评定参数，并计算出地面导线测量误差对贯通的影响为：

式中：m′x（1-j）-两近井点1与j在x′方向上的相对点位中误差；m△a-两条近井点后视边坐标方位角之间的相对中误差；Ry′1和Ry′j分别为导线点1和j与k点连线在y′轴上的投影长，如图1所示。

3.2联系测量对贯通面横向误差的影响分析

竖井的联系测量是隧道贯通测量中一个重要环节。它主要是通过竖井将地面控制点的坐标和方位角传递到地下隧道中，实现地下和地面控制网的统一。起始边方位角误差会使地下导线旋转一个小角度，从而引起贯通面上的误差，隧道线路越长，影响就越大。本节主要从联系测量对地下起始边方位角的影响及起始边误差对贯通误差的影响分析入手，介绍联系测量对横向贯通误差的影响。

图1　区间隧道示意图

3.2.1联系测量精度计算方法

（1）联系三角形法具体为在竖井内悬挂两根钢丝，与近井点组成联系三角形，通过测定联系三角形的边长及角度要素a、b、c、ω、α和a′、b′、c′、ω′、α′，来计算坐标及地下导线起始边的方位角，如图2所示。

图2　联系三角形法示意图

我们由地面△AO1O2解算出β，由地下△BO1O2解算出β′。

坐标方位角推算遵循小角、长边的原则，按照T→A→O2→O1→B→M路线推算地下起始边方位角。

（2）通常，我们在设计联系三角形时，遵循2个锐角都为小角的原则，如图1所示，当α和β均为小角度时，β角的计算可按下式进行：

对上式进行微分可得：

由误差传播律可得：

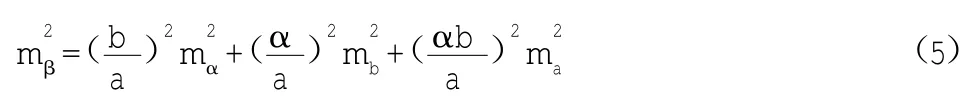
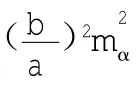
在此我们令：

我们设测边误差ms=ma=mb，则（7）式可变为：

由上式可知，如果要减小测距误差对待定角β的影响，应在布设联系三角形时使α角尽可能的小，即三角形应尽量布设成直伸三角形形式。

地下导线起始边的方向误差实质上是由地面、地下测边和测角误差联合影响造成，其影响值可用下式表示：

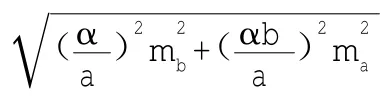
由公式（10）可知，地下导线起始边方位角的精度计算公式为：

（3）以厦门某地铁区间竖井联系测量为例，联系三角形的角度观测中误差为ma=±1.5″，边长观测中误差为ms=±0.8mm。我们按照观测角度α、边长a及b/a的不同独立进行3次联系测量，按照公式（11）计算的地下起始边方位角误差如表1所示。

表1　地下导线起始边方位角误差表（m0″）

3.2.2地下起始边误差引起k点在x′方向上的误差联系测量的重要内容就是传递井下起始边方位角，通常称为定向。而定向测量误差都集中反映在井下导线起始边坐标方位角误差上，所以定向测量误差引起的k点在x′方向上的误差为：

式中：m0-为地下导线起始边误差；ρ=206265″；Ry′0-为井下导线起始点与k点连线在y′轴上的投影长，如图1所示Ry′01和Ry′02。

则由1号井和2号井起始边引起的k点在x′方向上的中误差为：

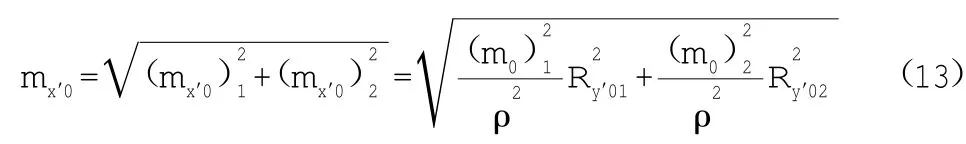
3.3地下导线测量引起的k点在x′方向上的误差分析

通常，地铁区间隧道的长度不会超过2km，而在设置施工竖井的情况下，贯通测量的长度还会进一步缩短，所以，一般地下导线的形式采用复测支导线形式。下面，我们分析支导线对k点在x′方向上的误差影响：

式中：mβ-为井下导线的测角误差；Ry′-为k点与导线点连线在y′轴上的投影长；α-为导线各边与x′轴间的夹角；ml-为测距边长误差。

因此，k点在x′方向上的误差为：

3.4贯通相遇点k在水平重要方向x′（横向）上的总误差

最终，由公式（1）、（13）、（14）可知，地面控制测量、联系测量和地下控制测量对贯通相遇点k在水平重要方向x′上，即对隧道贯通横向误差的综合影响可由下式表示：

4　应用示例

我们以厦门某地铁竖井区间为例，运用公式（15）来分析其在贯通面的横向误差。根据实际测量及计算成果，近井点1与j在x′方向上的的相对点位中误差为mx′（1-j）=8mm，近井点1与j后视方位角相对中误差m△a= 3.5″，Ry′1=318m，Ry′j=308m；1号井联系测量地下起始边方向误差（m0）1= 2.06″，Ry′01=296m，2号井联系测量地下起始边方向误差（m0）2=2.85″，Ry′02= 291m；地下导线测角中误差mβ=2.3″，导线点至贯通面的垂直距离分别为11′=204m、22′=77.6m、33′=66.7m、44′=195.5m（如图3），导线各边与x′方向的夹角分别为αx′01=88°14′21″、αx′12=85°30′16″、αx′23=84°16′30″、αx′34=87° 25′15″、αx′45=81°00′20″，导线测边中误差统一取ml=1.5mm。根据以上测量成果，代入公式（15），计算的贯通面横向中误差为：

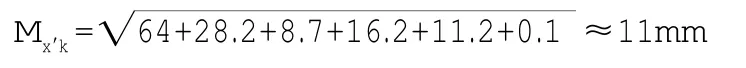
满足城市轨道交通测量规范关于隧道贯通横向中误差不超过50mm的规定。

5　结束语

由以上各节的分析可以看出，在观测条件不变的情况下，随着区间隧道线路的增长，贯通横向误差会逐渐增大，而一般情况下，地铁隧道区间的长度不超过2km。因此，我们主要考虑从地面控制测量，联系测量和地下导线测量三方面提高测量精度，从而最终提高贯通横向精度。由公式（15）及以上各节分析可知：①在地面控制测量过程中，需要提高点位精度及点位相对精度，除了保证地面控制网起算数据精度外，测量过程应严格按照规范执行；②竖井联系测量应尽量增大悬吊钢丝之间的距离a，一般a>5m，减小b/a值，使b/a<1，并使角α尽量小，一般α< 1°，同时，联系测量应独立进行若干次，以提高方向传递精度；③地下导线布设，在条件允许的情况下，应增加导线边长度，减少测角的个数，导线宜布设成直伸导线形式，同时，提高观测数据的精度。