结构抗震设计中振型分解反应谱法的应用与分析
2015-10-31高艺斌
高艺斌
(四川大学建筑与环境学院)
结构抗震设计中振型分解反应谱法的应用与分析
高艺斌
(四川大学建筑与环境学院)
计算结构地震作用效应时应根据一定的设计原则和假定条件对结构简化计算。本文对振型分解反应谱法理论做了研究,确立多质点体系的频率方程和振型方程,进而求解出各质点的地震效应。讨论了周期比对结构抗震影响以及各振型组合方法,为选取各阶振型提供依据,针对不同的振型组合得到各地震效应。
引言
随着我国经济的快速发展,高层建筑结构在大中小城市的越来越多的出现,其抗震性能的好坏决定着人民的生命财产安全。规范上规定高层建筑都要做抗震设计,须做地震水平作用和竖向作用对结构整体的分析。地震作用取决于地震烈度、距离震源的距离等因素有关,目前抗震分析中普遍采用振型分解反应谱法分析[2~3]。本文在前人研究基础上,研究振型分解反应谱的理论原理,推导各振型理论解、不同质点不同振型的理论解以及各振型组合情况。
1 抗震设计原则及假设
建筑结构的地震反应属于短时间发生的大变形问题,须按照弹塑性理论进行分析。按大变形对对强度验算,会造成材料的过度消耗。小震不坏,中震可修,大震不倒为结构三水准设防原则,抗震设计必须按照这一原则进行。丰定国[2]等人指出在不考虑竖向振动时,可以将框架各层看成一质点,分析有限质点受地震作用在水平方向的振动问题。各层等效的惯性力作用在各质点质心处,与外荷载构成力平衡体系。
2 反应谱法理论(如图1)
振型分解理论就是利用多质点体系自由振动特性来简化多质点体系强迫振动求解。即多质点体系振动问题,通过振型变为单质点振动组合问题来求解。
2.1各质点惯性力
多质点系统中,质点i上地震作用力等于该点的惯性力:

因各振型{Yi}(i=1,2,…,n)为独立的向量,则可将单位向量{1}由向量组{Y1}{Y2},…,{Yn}表示,即:
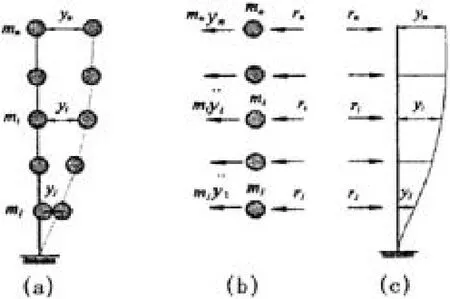
图1 多质点自由度体系简化图

其中ai为待定系数。等式两边同乘以{Yj}T[M],由振型正交性知,除了aj{Yj}T[M]{Yj}以外,其余的都等于零,得:
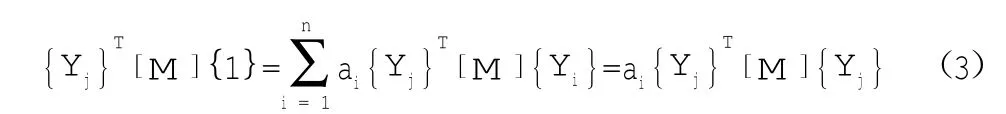
解得:

将式(4)代入式(2)中得:

2.2多质点振动频率和振型
多质点体系有阻尼运动方程表示:

根据振型正交性可知,体系中的地震位移反应向量{x}可表示为:

将式(7)代入式(6)中得:

将上式两边左乘{Yi}T得:

各振型与结构质量矩阵、刚度矩阵正交,并假定振型与结构阻尼矩阵也是正交的,即{Yi}T[C]{Yj}=0,i≠j。
则式(9)成为:
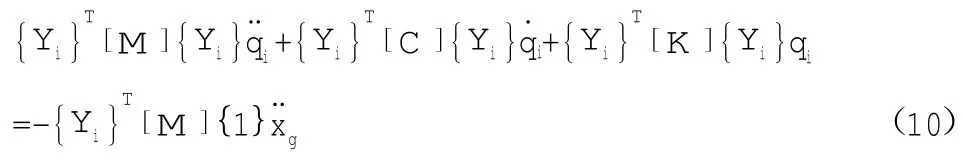
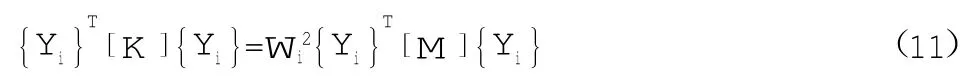
则得到:

令:

将式(10)两边同时除以{Yi}T[M]{Yi}得:

由杜哈密积分可得式(12)解为:
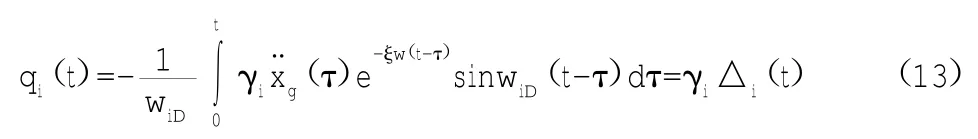
将式(13)代入式(7),即得多自由度体系的位移解:
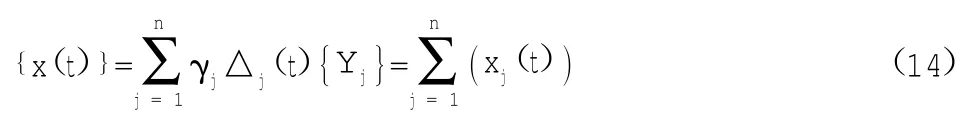
对任意质点i在任意时刻时的相对水平位移为:

则质点i在任意时刻时的相对加速度为:

水平地面的水平加速度表达成:

则质点i在任意时刻的水平地震作用力为

式中:fji为质点i的第j振型水平地震惯性力:

2.3水平地震作用力
令质点i的第j振型水平地震作用力为该阶振型最大惯性力,即:

将式(17)代入式(18)中得:

则由地震反应谱定义可将第i质点第j振型水平地震作用表达为:

由建筑结构地震影响系数与地震反应谱之间的关系可知:

式中:Gi为质点的重量;αi为相应于j振型自振周期的地震影响系数。
2.4振型组合方法
振型组合方式和整个结构的平面布置、空间布置、是否考虑扭转效应、结构体系是否均匀对称等方面有关;对于沿水平方向振动,可简化为多质点的弹性体系而言,一般可以采用平方和开平方法即SRSS法;对于结构体系因整体布置不规则须考虑扭转耦连效应的多质点体系来说,一般可以采用完全二次项组合法即CQC法。两者主要区别在于从数学角度讲SRSS法是建立在各独立事件的概率统计方法基础上,也就是说要求参与数据处理的各事件之间是相互独立的,不存在耦联关系;当考虑扭转耦联效应时各振型之间的频率间距小,相邻较高的振型频率近似,此时应考虑不同振型的相关性。当结构的自振频率相差较大时,可近似看成每个振型是相互独立的,采用SRSS法得到较好的结果。

图2 各自振周期比对应的耦联系数
对第j振型各质点水平地震作用,按静力方法计算,可得体系该振型下的最大地震效应。记体系第j振型某特定最大地震反应为Sj,而特定体系下的最大地震效应为Smax,则可以通过各振型的地震反应来估计Smax。
(1)当结构不进行扭转耦联计算时,采用平方和开方法(SRSS法)计算体系最大反应,即:

式中:Sj为在第j振型水平地震作用下产生的结构内力包括轴力、剪力和弯矩等。
(2)当结构考虑扭转耦联计算时,采用完全二次项组合法(CQC法),对于单向水平地震作用时,地震作用最大反应即地震作用标准值为:

当考虑双向水平地震作用时,按下式中得较大值确定:

或

式中:Sx、Sy分别是x方向和y方向单向水平地震作用按式(23)计算。
3 振型分解反应谱法采用的地震反应谱图形

图3 地震影响系数线
α为地震影响系数;αmax为地震影响系数最大值;T为结构自振周期;Tg为特征周期;η1为下降斜率调整系数;η2为阻尼调整系数;γ为衰减指数。
4 周期比对计算结果的影响
周期比是结构本身以扭转为主的第一振型周期Tt与以平动为主的第一振型周期T1之比。当结构的质心与刚度重心重合时,该情况只有单一平动或扭转变形,此时结构的周期和结构之间的周期比为非耦联的周期和周期比。如果结构的质心和刚度重心不重合时,这种情况下的周期和周期比须考虑结构之间相互耦联影响。
周期比控制是考虑结构侧向刚度和扭转刚度之间的相对关系,为了使抗侧力构件在平面空间上布置更坚固、更有效的起到抗震作用,防止产生大的扭转影响。调整周期比的原则为:结构抗侧力构件应布置尽可能的均匀对称;增加结构周边刚度;降低结构中部的刚度。
5 结论
(1)框架结构在水平地震作用下的振动响应,分析抗震设防的原理,为了能够达到预期设防效果,采用振型分解反应谱法能够较合理的计算建筑结构地震效应。振型分解法较底部剪力法等误差小,结果较精确。在复杂情况下,规范上给出了时程分析法来补充计算。地震分析时因属于大变形问题,应将结构进行弹塑性分析,结构处于弹性阶段截面强度设计。
(2)不论结构对称与否,结构的扭转偏心总是存在的,在实际工作中直接选用CQC法进行振型组合。振型组合方法的选择根据结构平面布置情况,是否考虑扭转效应来判断,对于多振型的结构可以仅计算2~3个振型即可。
(3)周期比是控制高层结构扭转的重要指标,在抗震设计时应满足规范规定的最低要求前提下,调整合理结构合理的刚度,进而提高结构抗震作用。
(4)本文对抗震计算的基本理论做了一定研究,为更好的研究地震动态响应分析提供一定的理论基础。在求解频率和振型时,需计算大型非线性方程组,应在提高计算精度方面做更多的研究。
[1]中华人民共和国住房和城乡建设部.《建筑抗震设计规范》(GB50011-2010)[S].北京:中国建筑工业出版社,2010.
[2]丰定国,王社良.抗震结构设计[M].北京:地震出版社,2006.
[3]李国强,李洁,苏小卒.建筑结构抗震设计[M].北京:中国建筑工业出版社,2002.
[4]郑文忠,闫凯.水平荷载下底部框架的内力计算方法[J].华中科技大学学报(自然科学版),2011,39(4):119~123.
[5]朱泽,冯继行.解析底部剪力法计算多自由度体系水平地震力[J].山西建筑,2013,39(8):24~25.
[6]王伟.反应谱法和时程分析法在高层抗震计算中的对比分析[D].华南理工大学,2012.
[7]吴珊珊,张季超,陈原.用分层法和D值法求解框架在竖向荷载作用下的内力[J].广州大学学报(自然科学版),2010,9(5):35~38.
TU834.36
A
1673-0038(2015)27-0049-03
2015-6-20
