多截面细径管结构参数对放气系统压降特性的影响
2015-10-31任旭东王小刚曾祥兵臧立青张方晓
任旭东,廖 彬,王小刚,曾祥兵,臧立青,张方晓
(中国工程物理研究院 总体工程研究所,绵阳 621900)
多截面细径管结构参数对放气系统压降特性的影响
任旭东,廖 彬,王小刚,曾祥兵,臧立青,张方晓
(中国工程物理研究院 总体工程研究所,绵阳 621900)
采用数值模拟方法研究了多截面细径管结构参数对放气系统压降特性的影响,得到了导管几何尺寸、导管内壁粗糙度和出口压力等参数对压降特性影响的变化规律。研究结果表明:缩短容器导管长度或扩大其内径对壅塞状态下的压降影响较小,但可以显著提高层流状态下气体的流动速度,从而减少放气时间;内壁粗糙度对壅塞状态下的压降特性影响较大,随着粗糙度的增大,压力下降速度有所降低,而对层流状态下的压降特性影响较小,在容器压力降至极低的情况下,粗糙度的影响可以忽略不计;出口压力对整个流动过程的放气速度影响较小,出口压力的进一步提高不会明显增加放气速度。该研究可为多截面细径管放气系统的优化设计提供依据。
放气系统;气体流动;多截面细径管;结构参数;压降
0 引言
细径管路系统多以不同尺寸的细径导管通过阀门或者其他连接结构组合而成,存在多处截面过渡区域,流场速度梯度较大。因此,如何提高细径管路的流速是一个难点。目前,基于经典连续气体介质动力学理论,对气体在传统管道中的流动已有广泛研究,并取得了成果,例如天然气管道流动[1-3]和喷管流动[4-5]等,但对细径管从中低压到真空环境中的流动研究较少。李明海等人针对低压环境下开口放气系统的结构设计,建立了容器压力变化公式,并结合试验结果对该公式进行了系数修正[6]。廖彬等人通过试验和理论分析相结合的手段研究了带细径导管的容器的放气性能影响因素,结果表明细径管内率先出现壅塞流动现象,并持续很长时间,随着压力的进一步下降,细径管内流动转为层流,并指出了容器的放气速度与气体种类、管道长度和截面尺寸、背压等因素的关系[7]。任旭东等人对大压差下多截面细径管内流动问题开展了数值模拟研究,并结合理论和实验结果详细地分析了多截面细径管内不同流动状态下气体流动特性[8]。但上述研究均未涉及多截面细径管内结构参数对压降特性的影响。
本文在文献[8]的研究基础上采用数值模拟方法研究多截面细径管结构参数对放气系统压降特性的影响。
1 数值模拟
包含了不同尺寸细径导管的放气系统内部流动情况比较复杂,要进行完全数值模拟比较困难,因此需对系统简化,如图1所示。简化模型中包括放气容器,3段不同内径、不同长度的细径管,3 m×3 m的模拟真空区域。由于简化后的模型结构以及气体流动是轴对称的,因此可将数值模拟简化为二维计算。

图1 放气系统简化模型示意图Fig.1 Schematic diagram of a simplified model of deflation system
采用FLUENT商用软件,基于有限体积法对图1的简化模型进行数值模拟。其中,流场控制方程采用二维非定常雷诺平均N-S方程,湍流模型采用标准的k-ε湍流模型,壁面边界均采用绝热条件和无滑移边界条件。考虑到细径管内流场速度梯度较大,温度和动量方程强烈耦合,对温度和密度所用的亚松弛因子进行了亚松弛处理。
2 算例验证
为验证数值模拟方法的正确性,建立了由放气容器、等截面圆管(φ1mm×100mm)和模拟真空区域组成的系统(见图2),分别采用解析公式(1)与上述数值模拟方法进行了求解。

图2 等截面圆管的系统模型示意图Fig.2 Schematic diagram of numerical model of straight tube
根据壅塞理论[9],当导管内出现壅塞现象时,质量流率达到最大值,为

式中:Qmax为壅塞状态时的质量流率,kg/s;S为导管出口截面积,m2;ρ为气体密度,kg/m3;P为入口压力,Pa;γ为比热比。
由式(1)可以看出,在壅塞状态下,导管内的质量流率仅与气体密度、入口压力有关,而与背压无关。即使背压进一步降低,也不能使出口截面的气流马赫数以及导管流量继续增加。
采用式(1)计算壅塞状态下等截面圆管的质量流率,结果为0.55 g/s。
图3为采用数值模拟方法得到的等截面圆管出口处的质量流率随时间变化的曲线。可以看出,圆管出口处的质量流率在极短的时间内达到了最大值,并且在随后的时间内基本保持不变。这表明在放气过程中等截面圆管内很快达到壅塞状态,此时质量流率约为0.59 g/s。
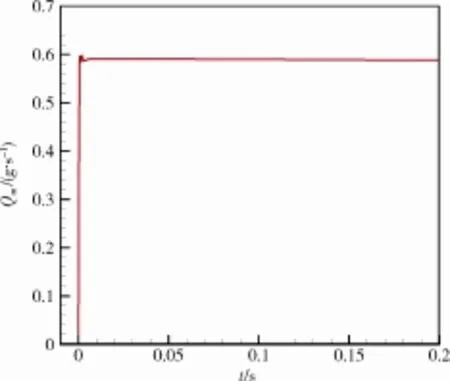
图3 圆管出口处的质量流率与时间的关系Fig.3 Relationship between mass flow rate and time at round tube outlets
可以看出,理论解析解与数值模拟解比较接近,验证了数值模拟方法的正确性。
图4为等截面圆管沿轴线的马赫数分布曲线。通过圆管轴线马赫数分布可以判断壅塞状态发生的位置。由图4可以看出,在横坐标的0.97处,中心气流马赫数达到1。这表明,在导管的出口区域,发生了流动壅塞现象,与理论分析一致。这也验证了该数值模拟方法的正确性。

图4 等截面圆管轴线马赫数分布Fig.4 Mach number distribution along the centerline of uniform-section round tube
3 结果与分析
3.1放气过程中导管内流态分析
以φ1mm×80mm(导管Ⅰ)+φ3mm×900mm(导管Ⅱ)+φ6mm×500mm(导管Ⅲ)3段细径管组成的放气系统模型为例,图5为细径管出口处的质量流率随时间变化的曲线。可以看出,导管Ⅰ出口处在极短的时间内质量流率达到了最大值,并且在随后的时间内基本保持不变,这表明产生了流动壅塞现象。随着时间的推移,导管Ⅱ和Ⅲ内也相继发生了流动壅塞现象。

图5 不同导管出口处的质量流率与时间的关系Fig.5 Relationship between mass flow rate and time at the outlets of different tubes
图6为壅塞状态时放气容器内压力随时间变化的曲线。对比数值模拟结果与试验结果可以看出:数值模拟计算结果与试验结果吻合较好;前120 s容器内压力下降非常快,压力梯度较大;压力的对数值与时间呈现较好的线性衰减关系。这是由于发生壅塞时质量流率与入口压力成正比,表征在容器内压力随时间呈对数衰减。容器内压力越小,壅塞持续时间越短。
随着放气容器内压力的进一步下降,壅塞现象消失,细径管内气体处于层流状态,容器压力下降较慢,如图7所示。根据层流理论[10],当管道内充分发展为层流流动时,通过圆管的体积流量为

图6 壅塞状态时容器内压力随时间的变化Fig.6 Pressure in the container vs.time under chocked flow conditions

图7 层流状态时容器内压力随时间的变化Fig.7 Pressure in the container vs.time under laminar flow

式中:Qm为体积流量,m3/s;ΔP为导管进出口压差,Pa;d为导管直径,m;µ为气体黏性系数,kg/(m·s);l为导管长度,m。
由式(2)可知,在层流状态下,流量与导管进出口压差成正比,与导管内径的4次方成正比,与导管长度成反比。层流状态时容器内压力下降需要更多的时间,主要原因是气流的流速受导管截面积和长度的限制而显著降低。
3.2导管内径对压降特性的影响
保持导管Ⅰ和导管Ⅲ的几何尺寸不变,通过改变导管Ⅱ的内径(见表1)考察其对压降特性的影响。图8为导管Ⅱ不同管径下放气容器内压力随时间变化曲线。

表1 4种细径管的几何尺寸Table 1 Geometry sizes of four kinds of small diameter tubes
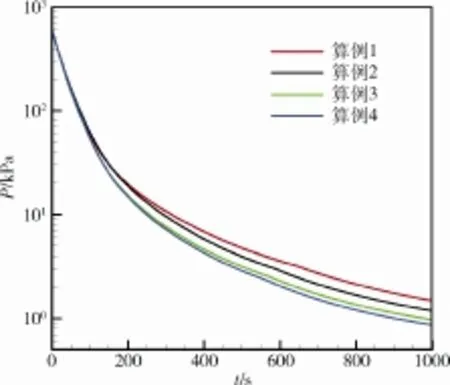
图8 导管Ⅱ不同内径下容器压力随时间的变化Fig.8 Pressure in the container vs.time for different inner diameters of tube 2
由图8可以看出:在初始阶段(即120 s之前),不同内径的导管Ⅱ下容器内压力下降基本一致,说明内径对放气效率影响较小。这是因为导管Ⅰ内已发生流动壅塞所致。随着放气时间的延长,不同内径导管Ⅱ下的容器内压力下降出现了分化,管径较大者,压力下降越慢。这是由于在层流状态时,导管的流量与导管内径的4次方成正比,内径越大,流量越大。
同时,比较不同内径导管Ⅱ在2 kPa时对应的放气时间(见表2),可以发现,随着导管内径的增大,放气时间缩短并接近。这表明,不能一味地靠增加内径来缩短放气时间。这是因为在层流状态下,串联导管总流导的倒数是不同管径导管流导的倒数之和[11],显然,管径小的导管对串联导管的流导贡献最大,在导管Ⅰ内径保持不变的条件下,只增加导管Ⅱ的内径不一定能大幅度提高整个导管的放气速度。

表2 2 kPa时对应的放气时间Table 2 Deflation time when P= 2 kPa
3.3导管长度对压降特性的影响
保持导管Ⅱ和导管Ⅲ的几何尺寸不变,通过改变导管Ⅰ的长度(见表3)考察其对放气性能的影响。图9为导管Ⅰ不同长度下容器压力随时间变化曲线。可以看出,在初始阶段(120 s之前),不同长度的导管Ⅰ下容器内压力下降基本一致,说明壅塞状态下长度对放气效率影响较小。随着放气时间的延长,不同长度导管Ⅰ下容器压力下降出现了分化,导管长度较大者,压力下降越慢。

表3 3种细径管几何尺寸Table 3 Geometry sizes of three kinds of of small diameter tubes

图9 导管Ⅰ不同长度下容器压力随时间的变化Fig.9 Pressure in the container against time for different lengths of tube 1
图10为以算例1(见表3)为基准,其余2种算例下容器压力到达同一值时所需时间之差的曲线。

图10 容器压力到达同一值时所需时间(以算例1为基准)Fig.10 Time needed to reach the same pressure for different wall roughness (calculation based on sample 1)
可以看出,在壅塞状态下容器压力达到同一值所需的时间之差较小,下降速度相差不大,这表明壅塞状态下改变导管长度对容器内压力下降影响较小;而在层流状态下,达到同一压力所需的时间差显著增加,这是由于导管的流量与其长度成反比,即长度越长则流量越小;此外,随着压力的持续降低,达到同一压力所需时间差曲线斜率越大,这意味着放气速度减慢的趋势更加明显,导管长度对该阶段的放气速度有着明显的影响。
因此,缩短容器导管长度对壅塞状态下的压降特性影响较小,但可以显著提高层流状态下气体的流动速度,从而缩短放气时间。
3.4内壁粗糙度对压降特性的影响
细径管尺寸越小,则导管内壁粗糙度对气体流动的影响越大,进而影响整个系统的压降特性。数值模拟中,内壁粗糙度通过导管壁面边界条件设置。
各算例中的导管内壁粗糙度见表4。图11为不同内壁粗糙度下容器压力随时间的变化曲线。

表4 算例中细径管内壁粗糙度Table 4 Wall roughness of small diameter tubes

图11 不同内壁粗糙度下容器压力随时间的变化Fig.11 Pressure in the container vs.time for different wall roughness
图12为以算例1(见表4)为基准,其余3种算例下容器压力到达同一值时所需时间之差的曲线。可以看出,在初始阶段,随着粗糙度的增大,容器压力下降速度降低,在壅塞流段,容器压力到达同一值时所需的时间之差呈上升趋势,这表明粗糙度对壅塞状态下的压降特性的影响较大。在层流段,容器压力到达同一值时所需的时间之差呈平稳下降趋势,这表明粗糙度对压降特性的影响随着层流持续时间的增长而降低,因而对压降特性影响较小;在容器压力降至极低的情况下,粗糙度的影响可以忽略不计。

图12 容器压力到达同一值时所需时间之差(以算例1为基准)Fig.12 Time needed to reach the same pressure for different wall roughness (calculation based on sample 1)
3.5出口压力对压降特性的影响
图13为不同出口压力(100、300、1000 Pa)条件下容器压力随时间变化的曲线。可以看出,在初始阶段,流动状态为壅塞状态时,不同出口压力条件下容器压力下降基本一致。这是由于壅塞状态下,气体的质量流率仅与导管入口参数(即容器内参数)有关,而与出口压力无关。当壅塞状态结束后,气体流动进入层流状态,在200~400 s时间段,不同出口压力条件下容器压力下降曲线也基本一致;在400 s之后,出口压力越小则放气速度越快,这是因为导管的流量与前后压差成正比,在层流开始阶段,出口压力很低,不同出口压力条件下的前后压差基本没有差异;当放气时间继续延长并容器压力进一步降低时,出口压力对放气速度有影响,出口压力越低,放气速度越快。

图13 不同出口压力下容器压力随时间的变化Fig.13 Pressure in the container vs.time for different outlet pressures
4 结论
本文采用数值模拟的方法研究了多截面细径管路结构参数对放气系统压降特性的影响,得到了不同结构参数对放气系统压降特性的影响变化规律:
1)缩短容器导管长度或扩大容器导管内径对壅塞状态下的压降特性影响较小,但可以显著提高层流状态下气体的流动速度,从而缩短放气时间。在工程应用中,受到系统布局的限制,需要综合考虑给出最佳参数。
2)内壁粗糙度对壅塞状态下的压降特性影响较大,随着粗糙度的增大,压力下降速度有所降低;而对层流状态下的压降特性影响较小,在容器压力降至极低的情况下,粗糙度的影响可以忽略不计。
3)出口压力对整个流动过程的放气速度影响较小,只有在放气容器压力极低的情况下才会影响放气速度。
(
)
[1]Jason M K, Daniel A C.Estimating sonic gas flow rates in pipelines[J].Journal of Loss Presentational in Process Industries, 2005, 18: 55-62
[2]叶学礼.天然气放空管路水力计算[J].天然气工业,1999, 19(3): 77-81 Ye Xueli.Hydraulic calculation of natural gas vent line[J].Natural Gas Industry, 1999, 19(3): 77-81
[3]刘庆堂.高压天然气管网动态模拟与壅塞流动特性研究[D].济南: 山东大学, 2010
[4]丁英涛, 谢君堂, 仲顺安.微型喷管内气体流动的流量壅塞现象[J].北京理工大学学报, 2006, 26(12):1056-1059 Ding Yingtao, Xie Juntang, Zhong Shun'an.Phenomenon of gas flow chocking in micro-nozzles[J].Transactions of Beijing Institute of Technology, 2006, 26(12): 1056-1059
[5]Kubo K, Miyazato Y, Matsuo K.Study of chocked flows through a convergent nozzle[J].Journal of Thermal Science, 2010, 19(3): 193-197
[6]李明海, 臧立青, 李超, 等.低压环境下放气系统的压降特性分析[J].兵工学报, 2007, 28(10):1234-1237 Li Minghai, Zang Liqing, Li Chao, et al.Analysis of pressure drop characteristics of deflation system under low atmospheric pressure environment[J].Acta Armamentarii, 2007, 28(10): 1234-1237
[7]廖彬, 臧立青, 甘勇, 等.容器放气性能影响因素试验研究[J].航天器环境工程, 2009, 26(增刊 1):103-108
[8]任旭东, 廖彬, 王小刚, 等.真空背压下多截面细径管内气体流动特性分析[J].真空科学与技术学报,2015, 35(2): 161-165 Ren Xudong, Liao Bin, Wang Xiaogang, et al.Modelling and simulation of gas-flow via narrow tubes with varied cross-sections into vacuum chamber[J].Chinese Journal of Vacuum Science and Technology,2015, 35(2): 161-165
[9]钱汝鼎.工程流体力学[M].北京: 北京航空航天大学出版社, 1989: 314-315
[10]王新月.气体动力学基础[M].西安: 西北工业大学出版社, 2006: 82-84
[11]达道安.真空设计手册[M].北京: 国防工业出版社,2006: 98-99
(编辑:许京媛)
Influence of structural parameters of a multi-sectional small diameter tube in a deflation system on the pressure drop characteristics
Ren Xudong, Liao Bin, Wang Xiaogang, Zeng Xiangbing, Zang Liqing, Zhang Fangxiao
(Institute of System Engineering, China Academy of Engineering Physics, Mianyang 621900, China)
The influence of the structural parameters of a multi-sectional long thin tube on the pressure drop characteristics of a deflation system is studied by numerical simulations, and the relationship between the structural parameters and the pressure drop characteristics is obtained.The results indicate that the flow velocity of the gas under laminar flow conditions is greatly increased by decreasing the length or increasing the inner diameter of the tube, but the pressure drop under chocked flow conditions is hardly affected by the change of structural parameters.The roughness of the inner tube has a great influence on the pressure drop under chocked flow conditions, but has a smaller influence on the pressure drop under laminar flow conditions.It is also found that the outlet pressure has nearly no influence on the deflation velocity during the whole flowing process, which means that the deflation velocity will not be increased by increasing the outlet pressure.These results provide some guidance for optimizing the design of smalldiameter tubes in the deflation system.
deflation system; gas flow; multi-section small diameter tube; structural parameters; pressure drop
V416.8
A
1673-1379(2015)06-0593-06
10.3969/j.issn.1673-1379.2015.06.005
任旭东(1989—),男,硕士学位,主要从事结构优化设计工作。E-mail: 475255713@qq.com。
2015-03-29;
2015-11-14
